НЕУСТОЙЧИВОСТЬ СВЕТОВЫХ ПУЧКОВ С НЕСТАЦИОНАРНЫМ ВОЛНОВЫМ ФРОНТОМ В ИНЕРЦИОННОЙ КУБИЧНОЙ СРЕДЕ
О.Л.Антипов, Г.А.Пасманик
В данной работе обсуждается возможность классификации световых волн по их способности возбуждать объёмные голограммы в среде с большой памятью.
Выявлены такие поля, которые записывают наиболее контрастные объёмные голограммы. Рассеяние подобных полей на записанной ими же голограмме приводит к обмену энергиями между отдельными компонентами световой волны, т.е. к их взаимодействию. При достаточно большой мощности излучения подобные поля обычно становятся неустойчивыми и их угловой спектр излучения при прохождении нелинейной среды изменяется слабо. В этом случае можно говорить об устойчивых полях.
Хотя разделение световых полей на устойчивые и неустойчивые в значительной степени условно, тем не менее, оно может оказаться полезным для анализа возможностей селекции световых сигналов на фоне шумов. Такая селекция может быть основана, например, на отличительном свойстве сигналов определенного вида наиболее эффективно возбуждать объемные голограммы в инерционной среде или, наоборот, на неспособности сигналов эффективно возбуждать такие голограммы. Это обстоятельство отличает данный вид нелинейной селекции линейной, при которой выделяется сигнал с заранее известной пространственно-временной структурой поля.
Задача нелинейной селекции может быть решена с помощью процессов вынужденного рассеяния (ВР) света в нелинейных средах. Так, в работах /1,2/ показана принципиальная возможность осуществления нелинейной селекции световых пучков при вынужденном мандельштам-бриллюэновском и комбинационном рассеяниях.
Для каждой разновидности ВР (попутного и обратного, стационарного и нестационарного) существуют свои наиболее неустойчивые структура световых пучков. Здесь мы обсуди) возможность селекции световых сигналов в нелинейных инерционных средах, в которых
- 15 -
осуществляются процессы типа попутных ВР крыла Релея и нестационарного вынужденного температурного рассеяния.
Отыскание наиболее неустойчивых структур световых пучков
Пусть на инерционную кубическую среду, изменение показателя преломления которой D
n под действием поля описывается уравнением
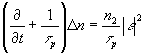 (1)
(1)
падает сильно неоднородное в пространстве и во времени излучение
e
0 = e0exp[i(w
0t - k0z)] + к.с., с постоянной по сечению средней интенсивностью - с плоской огибающей (t
р - время релаксации возмущений D
n, n2 - константа нелинейности). Найдем, какие комплексные амплитуды обеспечивают наиболее аффективное возбуждение пространственно-неоднородной (контрастной) голограммы - решетки показателя преломления.
Для этого предположим, что, кроме волны e
0, на входе в среду имеется также слабая волна возмущений e
1 = Е1еxp[i(w
0t – k0z)] + к.с. В результате интерференции этих волн в нелинейной среде возбуждаются возмущения D
n = D
ns + D
nint, где D
ns -характеризует самовоздействие волны e
0 в отсутствие волны e
1, D
nint - взаимодействие волн e
0 и e
1. Рассмотрим D
nint:
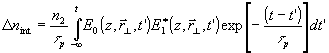 (2)
(2)
Эти возмущения удобно представить в виде:
D
nint = d
nint + <D
nint>
где угловые скобки означают усреднение по поперечному сечению s^
объёма взаимодействия.
В результате рассеяния волны e
0 на решетке d
nint в среде возбуждается нелинейная поляризация с комплексной амплитудой d
Р ~ d
ninte0, наличие которой может привести к подкачке
- 16 -
энергии в волну возмущения e
1. Эффективность нарастания этой волны зависит от того, насколько профиль нелинейной поляризации согласован с профилем поля волны e
1 во всём объёме взаимодействия, т.е. от того, насколько велика проекция e
1 на d
Р. Эта проекция определяется выражением:
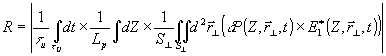 (3)
(3)
где t
u - длительность импульса световой волны, lp - характерная длина области рассеяния, примерно равная величине обратного инкремента для волны e
1.
Форма объёмной голограммы, а значит, и профиль d
Р, зависят от вида пространственно-временной структуры взаимодействующих полей e
0 и e
1. Поэтому эффективность нарастания волны e
1, в конечном итоге зависит от вида полей e
0 и e
ё. Поле световой волны e
0 будет наиболее неустойчиво по отношению к возмущению e
1, если пространственно-временные структуры исходного поля и поля возмущений таковы, что нормированный функционал r достигает максимума.
Поле исходного пучка e
0 при исследовании на устойчивость удобно представить с помощью разложения в ряд Фурье по времени и по поперечным координатам пучка:
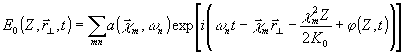 (4)
(4)
где множитель exp[-ic
2mz/2k0] характеризует влияние дифракции, а дополнительный фазовый набег j
(z,t) связан с самовоздействием светового пучка в нелинейной среде и для пучка плоской огибающей не зависит от поперечных координат 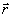 ^
.
^
.
Поле возмущения будем искать в виде:
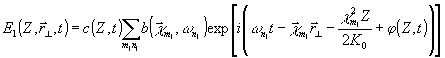 (5)
(5)
- 17 -
Перейдем к отысканию наиболее неустойчивых структур поля, которые обеспечивают максимум функционала r. Подставив (1), (2), (4), (5) в выражение (3), получим с учетом нормировки:
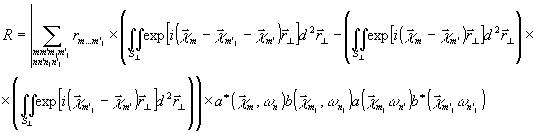 (6)
(6)
где
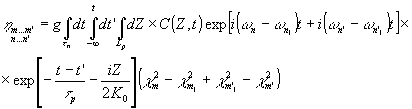 (7)
(7)
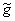 - константа, пропорциональная n2. Подынтегральное выражение в (7) является существенно знакопеременным на масштабе интегрирования. Ясно, что интеграл будет наибольшим, если показатель осциллирующих экспонент зануляется. Тогда этот интеграл можно представить в виде:
- константа, пропорциональная n2. Подынтегральное выражение в (7) является существенно знакопеременным на масштабе интегрирования. Ясно, что интеграл будет наибольшим, если показатель осциллирующих экспонент зануляется. Тогда этот интеграл можно представить в виде:
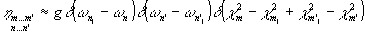 (8)
(8)
где 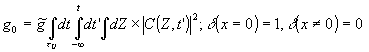 .
.
При этом мы считаем, что функция С(z,t) - медленная на масштабе интегрирования.
Аппроксимация (8) справедлива, когда выполнены условия:
k(D
q
)2m/lp << 1; m/t
pD
w
<< 1 (9)
где D
q
nD
w
соответственно, угловая расходимость и ширина частотного спектра волны e
0, М - полный инкремент для волны возмущений на длине всего нелинейного слоя.
Выполнение условий (9) фактически означает, что на характерном
- 18 -
масштабе временной 1/D
w
и пространственно 1/КD
q
2 модуляции волн эффекты нелинейного взаимодействия малы.
Будем рассматривать такой класс полей, для которых условия (9) выполняются. Тогда, подставив (8) в (6), получим:
r = r’ – r” (10)
где
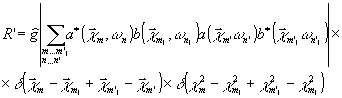 (11)
(11)
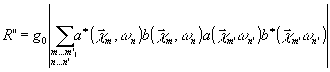 (12)
(12)
При усреднении по поперечному сечению s^
предполагалось, что граничные условия периодические.
Упростим выражение (11), используя прием, применяемый для анализа обращения волнового фронта составных световых пучков /3/.
Следуя /3/, от системы условий c
m - c
m1 + c
m’1 - c
m’ = 0 перейдем к эквивалентной системе (c
m - c
m1)(c
m’1 - c
m) = 0 и выделим три её независимых решения: c
m’1 = c
m’ + c
m1 - c
m
|
1) |
c
m = c
m1
c
m’ = c
m’ |
2) |
c
m = c
m’
c
m’ = c
m’1 |
3) |
(c
m - c
m1)(c
m’ - c
m) = 0
c
m1 ¹
c
m ¹
c
m’ |
(13) |
Рассмотрим выражение r для каждого из этих трех случаев (13).
В первом случае r обращается в нуль, т.к. r’ = r”. Легко видеть, что этот случай соответствует взаимодействию совпадающих по поперечной структуре полей Е0 и Е1: Е1 = с(t,z)e0, где с(t,z) - произвольная функция времени. Это означает наличие самовоздействия волны e
0. Такое самвоздействие, однако, не приводит к изменению углового спектра волны, проходящей через нелинейную среду. Поэтому мы на нем останавливаться не будем.
Рассмотрим функционал r, соответствующий второму решению системы (13): r2=r’2-r"2, где
- 19 -
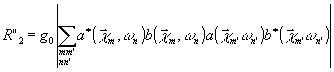
Найдем структуру полей Е0 и Е1, которые обеспечивают максимум r’2. Для этого представим r’2 в виде:
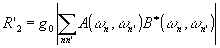
где
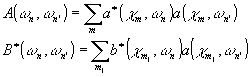
Необходимым условием максимума функционала r’2 является равенство: a(w
n,w
n’) = b(w
n,w
n’).
Для дальнейшего анализа r'2 удобно воспользоваться представлением попри Е0 и Е1 в виде рядов Карунена-Лоэва:
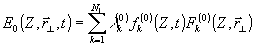 (14)
(14)
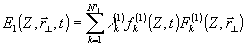 (15)
(15)
где
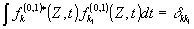
и
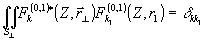
Сравнивая (14) и (4), (15) и (5), можно заметить, что Фурье-амплитуды a(c
m,w
n) и b(c
m,w
n) представимы в виде рядов:
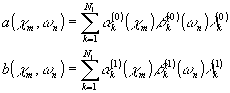 (16)
(16)
где наборы величин {a
(0,1)k(c
m) и {b
(0,1)k(c
m)} такие , что
- 20 -
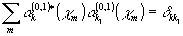 и
и 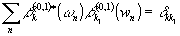 (17)
(17)
Подставляя (16) в (13). находим, что:
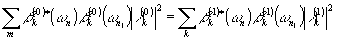
Воспользовавшись условием (17), получаем:
b
(0)k(w
n) = b
(1)k(w
n)|
l
(1)k|
/|
l
(0)k|
(18)
Легко видеть, что равенство (18) означает совпадение (с точностью до постоянного множителя) функций ¦
(1)k(z,t) и ¦
(1)k(z,t). В этом случае функционал r’z, равный (при нормировке Е0 на единицу)
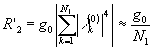
достигает максимального значения, если разложения Карунеyа-Лоэва (14), (15) имеют по одному члену, т.е. поля Е0 и e1 представлены в виде:
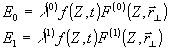 (19)
(19)
Теперь рассмотрим функционал r”. Условие минимума этого функционала является, по существу, условием наибольшей контрастности решетки D
nint. Легко показать, что функционал r" обращается в нуль, в частности, когда рассматриваемые поля Е0 и Е1 ортогональны (в смысле интегралов по поперечному сечению s^
). Для полей вида (14), (15) это означает, что 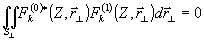 для любого k, Значит, комплексная амплитуда наиболее неустойчивого поля Е0, обеспечивающего максимум r2 = g0, и поля возмущений Е1 имеет вид:
для любого k, Значит, комплексная амплитуда наиболее неустойчивого поля Е0, обеспечивающего максимум r2 = g0, и поля возмущений Е1 имеет вид:
e0 = l
(0)¦
(z,t)f(z,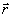 ^
), e1 = l
(1)¦
(z,t)f^
(z,
^
), e1 = l
(1)¦
(z,t)f^
(z,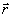 ^
)
^
)
- 21 -
где функции f и f^
ортогональны.
Факторизованный вид комплексной амплитуды поля соответствует полной пространственной когерентности пучка. Найденный нами результат, таким образом, означает, что пространственно-когерентный пучок неустойчив в нелинейной инерционной среде, но пространственная когерентность его в результате ВР не нарушается. Отметим также, что для некогерентного поля Е0 вида (14) и поля возмущений 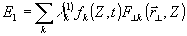 функционал r2 в раз меньше, чем для пространственно-когерентного.
функционал r2 в раз меньше, чем для пространственно-когерентного.
Наконец, рассмотрим функционал r, соответствующий условию
(c
m - c
m1)·(c
m' - c
m) = 0. Воспользовапа1ись этим условием, упростим выражение для r' вида (11). Для наглядности рассуждении перейдем в выражение (11) от суммирования по поперечным волновым векторам к интегрированию:
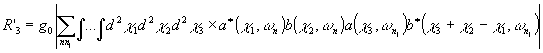
Введем новые векторы q = c
1 - c
2 и p = c
3 - c
1, которые в силу третьего условии (13) должны быть ортогональными. Воспользовавшись этим обстоятельством, а также изотропностью задачи (ни одно из направлений на плоскости поперечного сечения, заранее не выделено), от интегрирования по шестимерному пространству (c
1,c
2,c
3) перейдем к интегрированию по четырехмерному, пространству (q,р,c
q,c
p), где q = |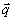 |
, р = |Р|
, где c
q = c
1·q/|
|
, р = |Р|
, где c
q = c
1·q/|
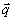 |
, c
p = c
1p/|
p|
. В этом случае r'3 можно представить в виде:
|
, c
p = c
1p/|
p|
. В этом случае r'3 можно представить в виде:
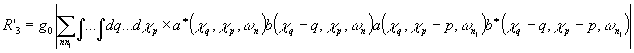
и после повторной замены c
q – q = c
q1, c
p – p = c
p1:
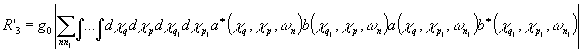
- 22 -
Теперь от интегралов вернемся к суммам:
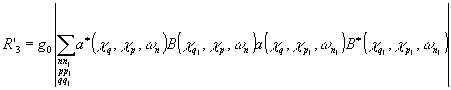
где a(c
q,c
р,w
n) и b(c
q,c
р,w
n) Фурье-амплитуды. Разложения полей Е0 и Е1, в базисе функций: exp[i(w
nt - c
px' - c
qy')], при z = 0, где x' и у' - проекции 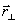 на оси декартовой системы координат, ориентация которых на плоскости поперечного сечения может быть произвольной.
на оси декартовой системы координат, ориентация которых на плоскости поперечного сечения может быть произвольной.
Функционал r'3 можно представить в виде:
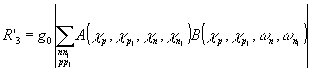
где
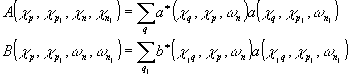
Необходимым условием максимума функции является равенство:
a(c
p,c
p1,w
n,w
n1) = b(c
p,c
p1,w
n,w
n1)
Вновь воспользуемся разложением полей в ряды Карунена-Лоэва. На этот раз удобно выбрать иной базис:
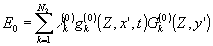 (20)
(20)
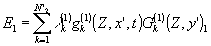 (21)
(21)
где
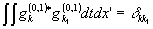
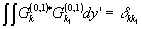
При этом Фурье-амплитуды представимы в виде рядов:
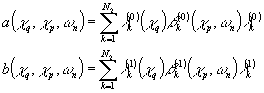
где для a
(0,1)k и b
(0,1)k выполняются условия:
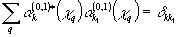
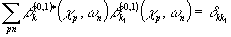
- 23 -
Проводя те же рассуждения, что и при анализе функционала r'2, можно показать, что r'3 достигает максимума, равного 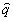 , когда комплексные амплитуды полей Е0 и Е1 имеют вид:
, когда комплексные амплитуды полей Е0 и Е1 имеют вид:
e0 = l
(0)g(z,x',t)g(0)(z,y'), e1 = l
(1)g(z,x',t)g(1)(z,y') (22)
Для произвольного поля (20) и поля возмущений 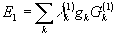 можно также найти, что значение r'3 равно g0/n2.
можно также найти, что значение r'3 равно g0/n2.
Записываемая полями Е0 и e1 голограмма будет контрастной (функционал r" обращается в нуль) в том случае, когда комплексные амплитуды полей ортогональны в смысле интеграла только по одной координате поперечного сечения пучка. Для рассматриваемых ролей это означает, что 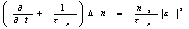 любого k.
любого k.
Значит, мы можем указать вид комплексной амплитуды еще одного сильно неустойчивого поля l
(0)g(z,x',t)g(z,y') и вид комплексной амплитуды поля возмущения l
(1)g(z,x't)g^
(z,y'), где g и g^
ортогональны, а также вид комплексной амплитуды поля возмущений для исходного поля e0 общего вида (20): 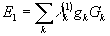 . Хотя количество членов в разложении (20) зависит от выбора ориентации осей x' и y' на плоскости поперечного сечения s^
, эффективность ВР от выбора ориентации этих осей не зависит и определяется минимальным числом членов в разложениях для всех возможных ориентации осей.
. Хотя количество членов в разложении (20) зависит от выбора ориентации осей x' и y' на плоскости поперечного сечения s^
, эффективность ВР от выбора ориентации этих осей не зависит и определяется минимальным числом членов в разложениях для всех возможных ориентации осей.
Таким образом, в результате анализа функционала r найдены пространственно-временные структуры наиболее неустойчивых в нелинейной инерционной среде полей: ¦
(z,t)f(z,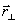 ) и g(z,x',t)g(z,y'). В результате их ВР нарастают поля с комплексными амплитудами ¦
(z,t)f^
(z,
) и g(z,x',t)g(z,y'). В результате их ВР нарастают поля с комплексными амплитудами ¦
(z,t)f^
(z,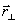 ) и g(z,x',t)g(z,y'). В разделах 3 и 4 будут определены инкременты этих полей, а также полей более общего вида в двух предельных случаях: стационарном, когда t
u >> t
p, и нестационарном, когда t
u << t
p.
) и g(z,x',t)g(z,y'). В разделах 3 и 4 будут определены инкременты этих полей, а также полей более общего вида в двух предельных случаях: стационарном, когда t
u >> t
p, и нестационарном, когда t
u << t
p.
- 24 -
Стационарное взаимодействие
Определим стационарные инкременты, характеризующие нарастание возмущений в поле пучка с нестационарным волновым фронтом. Прежде всего остановимся на пространственно-когерентных пучках, комплексная амплитуда которых на входе в нелинейную среду представима в виде: e0|
z=0=l
(0)¦
(t)f(r^
), где ¦
(t) - широкополосная функция времени, f(r^
) - сильно-неоднородная функция поперечных координат.
В линейной среде изменения комплексной амплитуды Е0 определяется соотношением Е0 = l
(0)¦
(t – z/vгр)f(z,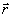 ^
). Значение l
(0) не зависит от z, а функция f удовлетворяет квазиоптическому уравнению:
^
). Значение l
(0) не зависит от z, а функция f удовлетворяет квазиоптическому уравнению:
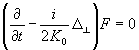 (23)
(23)
Рассмотрим сначала задачу о самовоздействии волны e
0 в нелинейной кубичной среде и определим в нулевом приближении характер изменения амплитуды l
(0). В этом приближении волна возмущения отсутствует и
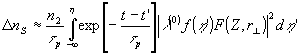
где h
= t – z/vгр.
Предположим, что флуктуации ¦
(0,t) происходят на масштабах t
~ 1/D
w
, существенно меньших, чем время релаксации t
р. Тогда D
ns=n2|
l
(0)|
2|
f|
2. Для простоты функция выбрана такой, что |
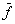 |
= 1, где значок "¾
" означает усреднение по времени на масштабе Т, много большем масштаба флуктуации функции ¦
, но меньшем времени релаксации t
р. Рассеяние волны e
0 на возмущениях D
ns приводит к возбуждению нелинейной поляризации
|
= 1, где значок "¾
" означает усреднение по времени на масштабе Т, много большем масштаба флуктуации функции ¦
, но меньшем времени релаксации t
р. Рассеяние волны e
0 на возмущениях D
ns приводит к возбуждению нелинейной поляризации
D
p ~ l
(0)|
l
(0)|
2´
|
f|
2´
f´
¦
Эту поляризацию удобно представить в виде
- 25 -
D
p ~ l
(0)|
l
(0)|
2(s
f + 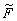 )
)
где s
= <|
f|
4>/<|
f|
2>. Для сильно неоднородных по поперечному сечению полей s
=2<|
f|
2> в дальнейшем будем считать <|
f|
2> = 1. Часть поляризации, пропорциональная 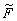 , как легко показать, играет роль шумового источника и не приводит к изменению комплексной амплитуды световой волны.
, как легко показать, играет роль шумового источника и не приводит к изменению комплексной амплитуды световой волны.
Поэтов приближенно можно считать, что D
p~2l
(0)|
l
(0)|
2f¦
. Наличие этой поляризации приводит к изменению амплитуды l
(0) согласно уравнению:
dl
(0)/dz = -2ig|
l
(0)|
2l
(0) (24)
где g = 2k0n2/n0.
Решение этого уравнения дает: l
(0)(z) = l
(0)(0)exp[-2ig|
l
(0)|
2z].
Перейдем теперь к определению инкремента для волны возмущений.
Пользуясь результатами раздела 2 для исходной волны вида ¦
fl
(0)(z), волну возмущений будем искать в виде ¦
f^
l
(1)(z)exp[-iW
h
]. Если функции поперечных координат f и f^
совпадают: f = const·f^
, то наряду со стоксовой компонентой e-iW
h
необходимо учитывать антистоксову компоненту еxp[iW
h
] в волне возмущений. Взаимодействие этих компонент приводит к уменьшению инкремента до нуля. (Аналогичное гашение инкремента имеет место для плоской монохроматической волны, которая устойчива относительно соосных с ней возмущений).
В случае же ортогональности f и f^
взаимодействие стоксовой и антистоксовой отсутствует и поэтому достаточно ограничиться только одной стоксовой компонентой в волне возмущений. В результате интерференции волн e
0 и e
1 в среде наводятся возмущения показателя преломления
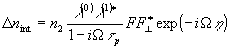 (25)
(25)
Рассеяние падающей волны на решетке D
nint приводят к изменению
- 26 -
амплитуды l
(1):
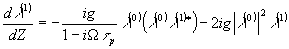 (26)
(26)
Решение этого уравнения показывает, что волна в e
0 вида ¦
´
f неустойчива по отношению к возмущениям вида ¦
´
f^
´
exp[-iW
h
], которые нарастают с инкрементом интенсивности 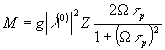 , достигающем максимума m = g|
l
(0)|
2z при W
=1/t
p.
, достигающем максимума m = g|
l
(0)|
2z при W
=1/t
p.
Если пучок падающего излучения не является пространственно-когерентным, то он представляется в виде суммы пространственно-когерентных мод:
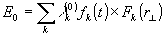 (27)
(27)
В линейкой среде изменения комплексной амплитуда Е0 определяются формулой
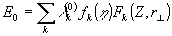
где fk - удовлетворяет линейному квазиоптическому уравнению.
Вследствие самовоздействия этой волны наводится голограмма D
ns:
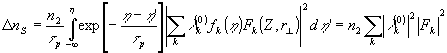
Рассеяние каждой из пространственно-когерентных мод на этой голограмме приводит к изменению ее амплитуды:
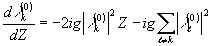 (28)
(28)
т.е. 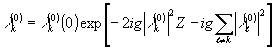
Если к волне 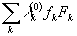 добавить волну возмущений
добавить волну возмущений 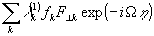 , то из-за интерференции волн возбуждается голограмма:
, то из-за интерференции волн возбуждается голограмма:
- 27 -
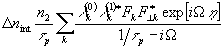
Рассеяние на ней мод падающей волны приводит к изменению амплитуд возмущений:
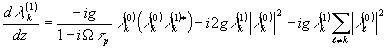 (29)
(29)
Отсюда следует, что при 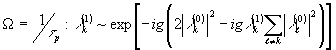 , т.е. с наибольшим инкрементом М = g|
l
(0)k|
2z нарастает волна возмущения, повторяющая по своей временной структуре наиболее интенсивную моду падавшей волны и имеющая ортогональное ей поперечное распределение.
, т.е. с наибольшим инкрементом М = g|
l
(0)k|
2z нарастает волна возмущения, повторяющая по своей временной структуре наиболее интенсивную моду падавшей волны и имеющая ортогональное ей поперечное распределение.
Если 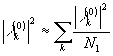 , где n1 - характерное число членов в разложении (27), то М=giz/n1, где
, где n1 - характерное число членов в разложении (27), то М=giz/n1, где 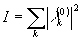 - средняя интенсивность излучения.
- средняя интенсивность излучения.
Перейдем теперь к анализу вопроса об устойчивости волны, представимой на входе в среду в виде:
e0|
z=0 = l
(0) g(x,t)g(y) (30)
где x и y - декартовы координаты и g(x,t) - функция с независимым временным изменением в разных точках оси у. В линейной среде изменение Ео определяется соотношением:
e0 = l
(0) g(z,x,t - h
)g(z,y) (31)
Значение l
(0) в линейной среде не зависит от z , а функция удовлетворяет уравнению (23).
Самовоздействие такой волны в нелинейной среде приводит к возбуждению объемной голограммы:
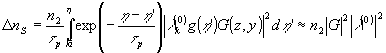
Мы предполагаем, что в любых точках Х: |
g(z,xh
)|
2 = 1.
- 28 -
Рассеяние падающей волны на этой голограмме приводит к изменению амплитуды l
(0):
-.2aw , w
Решение (31): l
(0) = l
(0)(0)еxp[-2ig|
l
(0)|
2z].
При отыскании инкремента неустойчивости волны (30) вновь воспользуемся результатами раздела 2 и волну возмущений будем искать виде l
(0)gg^
exp[-iW
h
] (в случае ортогональности g и g^
взаимодействия стоксовой и антистоксовой компонент возмущений не происходит и можно учитывать лишь стоксову компоненту). В результате рассеяния волны Е0 на решетке 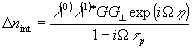 происходит изменение амплитуда l
(1), которое при W
= 1/t
р, как нетрудно показать, описывается выражением: l
(0)(я)=l
(1)(0)exp[-2ig|
l
(0)|
2z+|
l
(0)|
2z(g/2)(1-i)], т.е. инкремент неустойчивости волны вида (30) определяется тем же значением |
l
(0)|
2gz, что и инкремент неустойчивости плоской волны с амплитудой равной l
(0). Пусть теперь на входе в нелинейную среду имеется волна
происходит изменение амплитуда l
(1), которое при W
= 1/t
р, как нетрудно показать, описывается выражением: l
(0)(я)=l
(1)(0)exp[-2ig|
l
(0)|
2z+|
l
(0)|
2z(g/2)(1-i)], т.е. инкремент неустойчивости волны вида (30) определяется тем же значением |
l
(0)|
2gz, что и инкремент неустойчивости плоской волны с амплитудой равной l
(0). Пусть теперь на входе в нелинейную среду имеется волна
e0|
z=0 = 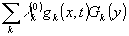 (32)
(32)
и волна возмущений Е1|
z=0 = 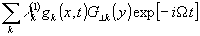 в результате самовоздействия волны Е0 у каждой амплитуды l
(0)k появляется дополнительный фазовый множитель:
в результате самовоздействия волны Е0 у каждой амплитуды l
(0)k появляется дополнительный фазовый множитель: 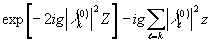 .
.
Из-за взаимодействия в инерционной кубической среде волн Е0 и Е1 возбуждается голограмма:
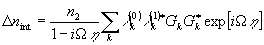
рассеяние на которой каждой из мод gkgk приводит к изменению амплитуд волны возмущений:
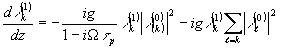 (33)
(33)
При W
= h
l
(1)k/t
p ~ exp[(g/2)|
l
(0)k|
2z], т.е. с наибольшим
- 29 -
инкрементом интенсивности М = g|
l
(0)k|2z нарастает волна возмущений, повторяющая по координате Х и времени t наиболее интенсивную моду в падающей волне и имеющая ортогональное к ней. распределение поля по координате у.
Если 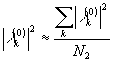 , где n2 - характерное число членов в разложении (32), то
, где n2 - характерное число членов в разложении (32), то 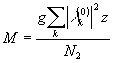 .
.
Аналогичным образом обстоит дело, если на входе в нелинейную среду имеется волна
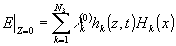 (34)
(34)
В этом случае оценка инкремента её неустойчивости дает:
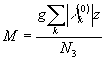 , где n3 - характерное число членов в разложении (34).
, где n3 - характерное число членов в разложении (34).
Сопоставление рассмотренных здесь примеров показывает, что в общей случае инкремент, характеризующий неустойчивость волны с нестационарным волновым фонтом, определяется минимальным числом nmin = min(n1,n2,n3) в одном из трех возможных разложений Карунена-Лоэва и примерно равен m = giz/nmin. Поскольку выбор декартовых координат произволен, то, очевидно, распад световой волны быстрее всего происходит относительно тех осей, где число n2 или n3 - минимально (если n1 >n2,n3).
Полученные формулы позволяют примерно оценить инкремент теплового самовоздействия многомодового многочастотного некогерентного излучения. Если, например, непрерывный световой пучок с шириной спектра D
w
и расходимостью q
проходит через поглощающий слой длиной l и коэффициентом поглощения a
[cm-1], то нарастание возмущений приводит к существенному уширению его углового спектра, если инкремент возмущений превышает несколько единиц. Для таких процессов 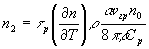 , где r
cp - теплоемкость единицы объема среды, t
р»
¦
q2, ¦
~ коэффициент температуропроводимости (t
р характеризует время релаксации решетки D
h с поперечным волновым вектором
, где r
cp - теплоемкость единицы объема среды, t
р»
¦
q2, ¦
~ коэффициент температуропроводимости (t
р характеризует время релаксации решетки D
h с поперечным волновым вектором 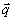 ). В обычных условиях эксперимента для некогерентного излучения D
w
t
>> q
/q
g и поэтому значение nmin=q
/q
g, где q
g = 4/kd - дифракционная расходимость пучка диаметром d. Для наблюдения эффекта уширения
). В обычных условиях эксперимента для некогерентного излучения D
w
t
>> q
/q
g и поэтому значение nmin=q
/q
g, где q
g = 4/kd - дифракционная расходимость пучка диаметром d. Для наблюдения эффекта уширения
- 30 -
углового спектра некогерентного излучения инкремент должен составлять 2¸
3. Это означает, что яркость излучения В = di/dW
t (W
t = p
q
2/4 - телесный угол. в пределах которого сосредоточен угловой спектр падающей волны) должна удовлетворять условию:
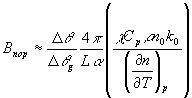 (35)
(35)
например, при q
/q
g »
10, a
l »
0,3, c
= 10-3см2/с, 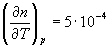 1/град, Ср = 107 эрг/г.град, r
= 1 г/см3, k0 = 105 см-1, В = 108 Вт/
1/град, Ср = 107 эрг/г.град, r
= 1 г/см3, k0 = 105 см-1, В = 108 Вт/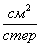 . Эффект уширения углового спектра излучения с яркостью В ~ 108 Вт/см2стер за поглощающей средой наблюдался в /4/.
. Эффект уширения углового спектра излучения с яркостью В ~ 108 Вт/см2стер за поглощающей средой наблюдался в /4/.
Нестационарное взаимодействие
Перейдем к анализу нестационарного взаимодействия и определим нестационарный инкремент возмущений в поле световой волны с длиной импульса, меньшей времени релаксации t
р. Рассмотрим сначала пространственно-когерентное излучение. Самовоздействие такого излучения, как нетрудно показать, описывается уравнениями:
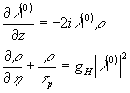 (36)
(36)
где r
(z,h
), определяется соотношением D
ns = r
|
f|
2, gh=g´
t
p (так как g ~ 1/t
p, то gh не зависит от Ср). Решение системы (36) при 1/t
p =0 имеет вид:
l
(0)(z) = l
(0)(0)exp[-2igh|
l
(0)|
2x
], где x
= zh
(37)
Для оценки инкремента допустим, что волна возмущений имеет вид: Е1=l
(1)¦
f^
. В результате интерференции возбуждается объемная голограмма, для которой:
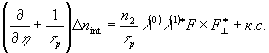
Вводя обозначения D
nint = r
ff^
, находим:
¶
l
(1)/¶
z = -il
(0)r
- i|
l
(0)|
2t
p(1 – exp[-h
/t
p)] (38)
- 31 -
¶
r
/¶
h
+ r
/t
p = ghl
(0)l
(1)*
Решение этих уравнений показывает, что при l
(0)(z), определяемой формулой (37) и 1/t
р = 0, экспоненциальный рост возмущения отсутствует. Таким образом, в существенно нестационарном режиме t
/t
р << 1 распад падающих на кубичную среду пространственно -когерентных волн подавляется (см. также /5/).
В первом приближении по параметру h
/t
р решение (38) показывает, что
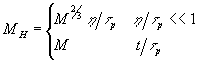
где m = g|
l
(0)|
2z.
Для ответа на вопрос об устойчивости волны вида g´
g рассмотрим сначала более простой случай, когда падающая волна является плоской по одной из поперечных координат и имеет нестационарный волновой фронт по другой: e0|
z=0=l
(0)g(x,t). Добавка к этой волне волны возмущений, которая из входа в среду имеет вид l
(1)g(x,t)exp[ic
yy], приводит к созданию объемной голограммы, изменение которой во времени описывается уравнением:
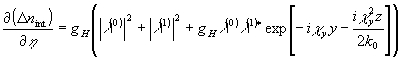
Вводя обозначения:
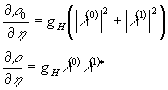 (39)
(39)
и воспользовавшись уравнением для поля, получим:
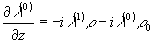 ,
, 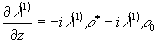 (40)
(40)
При |
l
"|
<< |
l
(0)|
находим, что l
(1) ~ 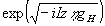 .
.
Таким образом, входная волна вида l
(0)g(x,t) - неустойчива с инкрементом интенсивности 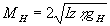 . Интересно, что замена переменных в системе (39), (40) допускает приближенное аналитическое решение, описывающее нелинейный режим процесса.
. Интересно, что замена переменных в системе (39), (40) допускает приближенное аналитическое решение, описывающее нелинейный режим процесса.
- 32 -
Это решение указывает, что в результате нелинейного взаимодействия интенсивность двух волн с увеличением параметра сравнивается между собой, но их выравнивание происходит с осцилляциями, период которых уменьшается с увеличением x
.
Если волна возмущений представляет сумму большого числа плоских по одной из поперечных координат волн, т.е. полное поле можно записать в виде:
e = l
(0)g(z,x,h
) + l
(1)g(z,x,h
)g(z,y)
то уравнения (39), (40) модифицируются:
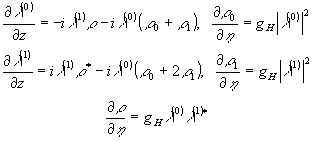 (41)
(41)
При |
l
(1)|
<< |
l
(0)|
их решение качественно не изменяется. Однако, из-за многомодового характера волны возмущений "сила" её самовоздействия удваивается (в правую часть уравнения (41) для l
(1) входит коэффициент 2 перед r
1). В силу этого нелинейная динамика взаимодействия волн в рассматриваёмом случае изменится. Решение (41) показывает, что при z´
h
®
¥
вся энергия волны l
(0)g(z,x,h
) перекачивается в волну возмущать l
(1)g(z,x,h
)g(z,y) независимо от соотношения между начальными интенсивностями.
Перейдем к вопросу о самовоздействии и устойчивости волны вида Е0=l
(0)g(z,x,h
)g(z,y). Раскладывая функцию g(y) в ряд Фурье: 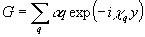 и вводя обозначение
и вводя обозначение
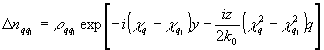 , находим:
, находим:
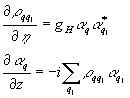 (42)
(42)
Замена x
= z´
h
позволяет проанализировать уравнение (42). Оказывается, что при gh|
a
q(0)|
2x
< 1 или gh(|
a
q(0)|
2 - |
a
q1(0)|
2)x
< 1
- 33 -
Таблица
| |
Вид поля |
Самовоздействие |
Взаимодействие |
Вид возмущения |
|
Неустойчивые поля |
¦
(t)f(x)exp[ic
xx+ic
yy] |
1 |
1 |
¦
(t)exp[ic
'xx+ic
'yy] |
|
¦
(t)f(x)exp[ic
yy] |
2 |
2 |
¦
(t)f^
(x)exp[ic
'yy] |
|
g(x,t)exp[ic
yy] |
1 |
1 |
g(x,t)exp[ic
'yy] |
|
Устойчивые поля |
¦
(t)f(x,y) |
2 |
1 |
¦
(t)f^
(x,y) |
|
g(x,t)g(y) |
2 |
1 |
g(x,t)g^
(y) |
|
¦
(t)f1(x)f2(y) |
4 |
2
1 |
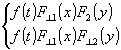
|
- 34 -
обмен энергиями между плоскими компонентами a
q происходит очень медленно и угловой спектр излучения за нелинейным слоем не изменяется, т.е. волна устойчива.
Отличие в процессе нестационарного распада многомодовой волны Е0 = l
(0)gg с сильно неоднородной функцией g(у) от плоской волны l
(0)g связано с тем, что самовоздействие многомодовой волны происходит в два раза эффективнее, чем взаимодействие этой же волны с любой выделенной гармоникой. Вследствие этого, относительно быстрое изменение фазы, связанное с самовоздействием волны как целого, подавляет развитие неустойчивостей.
Результаты нестационарного взаимодействия резюмированы в табл.. В её верхней половине указаны неустойчивые поля, инкремент которых зависит от энергии всей волны как целого. В столбцах "самовоздействие" и "взаимодействие" указаны численные коэффициенты, характеризующие "силу" данного процесса. Если эти "силы" совпадают, то взаимодействие волн эффективно и волна неустойчива, если же совпадение отсутствует, то волна устойчива (в том смысле, что её инкремент зависит не от полной интенсивности излучения, а от её распределения по Фурье-гармоникам и поэтому обратно пропорциональным числу гармоник).
Волна произвольного вида e0(z,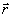 ^
,h
) в рассматриваемом классе нестационарных процессов, очевидно, является устойчивой
^
,h
) в рассматриваемом классе нестационарных процессов, очевидно, является устойчивой
Литература
1. Беспалов В.И., Манишин В.Г., Пасманик Г.А., ЖЭТФ, 1979, 77, в.11, с. 1756.
2. Бетин А.А., Манишин В.Г., Пасманик Г.А. Изв. АН СССР, сер.физ. 1981. № 6. с.950.
3. Басов Н.Г., Зубарев И.Г. В сб. "Обращение волнового фронта излучения в нелинейных средах", Горький. 1982, с.122.
4. Чиркин А.С., Юсупов Ф.М. Письма в ЖТФ. 1981, 7, в.13, с.805-809.
5. Духовный А.М., Стаселько Д.И. Письма в ЖТФ, 1982, 8, вып.16, с.1009-1014.

