|
|
 |
 |

|
| |
ОПТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА С ПРЕОБРАЗОВАНИЕМ ВОЛНОВОГО ФРОНТА
Н.Г.Власов, Г.Г.Левин
Рассмотрены принципы построения оптических систем, позволяющих осуществить прямые измерения физических характеристик. Новый подход предполагает решение некоторых уравнений в оптическом измерительном тракте. При этом предполагается использование исследуемого объекта в качестве функционального элемента решающей системы.
В настоящее время разработано большое количество различных измерительных методов, позволяющих определить практически любые физические характеристики, достаточно полно и достоверно описывающие исследуемые объекты к процессы. Объём регистрируемой информации при этом зачастую очень велик и требует для получения количественных результатов использования вычислительной техники. Особенно важен этап обработки при косвенных измерениях, когда регистрируемая величина связана с интересующими исследователя параметрами объекта сложными функциональными соотношениями.
С целью оперативной обработки информации и представления её в виде, удобном для интерпретации вместо традиционного обращения к ЭВМ, всё чаще используют специализированные, в том числе оптические, процессоры, предназначенные для решения конкретной задачи анализа данных, полученных в процессе эксперимента.
Отметим, что с точки зрения обеспечения оперативной обработки информации оптико-физические измерения обладают уникальными возможностями. Они обусловлены тем, что носителем информации об исследуемом объекте или процессе служит оптическое излучение. Это позволяет, в принципе, выполнять те или иные преобразования волнового фронта до этапа регистрации, что облегчает дальнейшую обработку
- 5 -
и получение количественных данных. Действительно, анализ литературных данных показывает, что в последние годы появились оптические измерительные устройства, содержащие отдельные элементы .преобразования волнового фронта, например, в интерферометрии /1/, томографии /2/, лазерной анемометрии /3/ и т.д.
Однако, ставшее традиционным последовательное расположение сначала экспериментальной установки, а затем оптической схемы обработки не всегда является оптимальным. Целый ряд преобразований волнового фронта, соответствующий определенным математическим операциям, не может быть выполнен после того, как зондирующее излучение уже выведено из непосредственно измерительного тракта устройства.
В данной статье рассматривается более общий подход к решению задачи получения количественных данных в оптико-физических измерениях, заключающийся в том, что сама схема экспериментальной установки продумывается и собирается так, чтобы ряд необходимых математических операций выполнялся в ней самой непосредственно в процессе исследования. При таком подходе экспериментальная установка и процессор перестают быть отдельными функциональными единицами, а составляют единое целое. В некоторых случаях все необходимые преобразования волнового фронта могут быть выполнены в оптической схеме измерительной системы без привлечения дополнительных элементов на его выходе, а сам объект является функциональным элементом схемы, выполняющим определённые преобразования волнового фронта. Такой подход позволяет от двуступенчатого процесса косвенных оптических измерений перейти к одноступенчатому способу прямых и непосредственных измерений. Это даёт возможность на выходе оптической измерительной системы получать непосредственно физические характеристики. интересующие исследователя.
Можно выделить следующие достоинства измерительных устройств такого рода: во-первых, расширение (функциональных возможностей , т.к. обработке подвергается непосредственно волновой фронт, во-вторых, увеличение отношения сигнал/шум, т.к. исключаются шумы регистратора, и, в-третьих, значительное сокращение временя обработки вплоть до реального времени,
Конкретные оптические схемы такого рода измерительных устройств
- 6 -
во многом определяются свойствами объекта и той физической величиной, которая измеряется в процессе исследования. Для широкого класса косвенных оптических измерений искомая величина ¦
, описывающая те или иные свойства объектов, связано с волновым фронтом поля z, прошедшего через объект либо отраженного от него некоторым оператором А:
z = a¦
(1)
В достаточно общем случае при оптических измерениях можно исключить этапы регистрации сигнала и его преобразования, тогда задача сводится к такой обработке волнового фронта, которая позволила бы решить уравнение (1).
Для большого класса задач уравнения, описывающие взаимосвязь этих величин, являются интегральными уравнениями (ИУ) первого рода. Остановимся на некоторых методах решения этих уравнений в оптических измерительных системах. При этом можно выделить два вида оператора А. К таким типам ИУ относятся часто встречающиеся в косвенных измерениях преобразования Абеля, Фурье, Радона, уравнение типа свертки и т.д. Для вычисления формул обращения некоторых из них могут быть использованы достаточно простые и широко известные схемы ОП, которые для целого ряда случаев могут дать хорошие результаты. Так, например: использование спектроанализатора для анализа оптического волнового фронта, прошедшего через гидродинамический турбулентный процесс: определение спектра турбулентных пульсаций, применение коррелятора, позволяющего определить масштабы турбулентности; реализация простейших методов пространственной фильтрации в лазерных анемометрах, позволяющая одновременно определять размеры и скорость частиц в потоке /4/ и т.д.
Во втором, наиболее часто встречающемся случае построение обратного оператора А -1 и использование ОП невозможно, и для решения задач такого типа требуется привлечение новых идей, обсуждаемых в данной статье. В этом случае целесообразно применение итерационных алгоритмов /5/. При использовании итерационных методов искомая функция определяется (в общем виде) по формуле:
- 7-
¦
к+1 = z + (1 - l
a)c¦
к (2)
где ¦
к - результат к-той итерации, 1 - единичный оператор , С - оператор, несущий некоторую априорную информацию об объекте, l
- параметр. Нетрудно показать /5/, что большинство известных итерационных схем, использовавшихся ранее как алгоритм Ван-Циттера и его модификаций, Гершберга, Фенапа и т.д., сводятся к уравнению (2).
Основные достоинства итерационных алгоритмов вытекают из уравнения (2). Во-первых, не нужно искать обратный оператор, во-вторых, привлекать любую априорную информацию об объекте, такой информацией может быть ограничение сигнала ила его спектра по полосе, положительность функции, определяющей объект, её гладкость, точное значке её на определенных участках и т.д. Вся эта информация описывается оператором С и легко вводится в алгоритм. Для реализации итерационной процедуру в процессе измерения необходимо выполнить целый ряд достаточно сложных преобразований волнового фронта. Однако, в последние годы В целом ряде работ /6,7/ было предложено рассматривать ОП, использующие оптические системы с обратной связью /8,9/, как процессоры, реализующие те или иные итерационные алгоритмы.
В процессе вычисления выражения (2) в оптической системе с обратной связью необходимо многократное выполнение оператора А. Он определяется тем преобразованием волнового фронта, которое осуществляет объект над зондирующим излучением. Текли образом, реализация оператора А связана с функциональным использованием объекта, как элемента оптического измерительного устройства, выполняющего определенные преобразования волнового фронта. Это требует такого построения экспериментальной установки, чтобы необходимые преобразования зондирующего излучения осуществлялись в процессе измерения. Не останавливаясь на особенностях выполнения тех или иных преобразований в ОП, отметим только, что техника оптических систем с обратной связью интенсивно развивается. Это позволяет надеяться на их широкое применение в оптических измерительных приборах и устройствах.
- 8 -
Рассмотренный выше подход к получению количественных данных в оптико-физических измерениях, основанный на выполнении в самой измерительной системе преобразований волнового фронта, был успешно реализован в целом ряде методов. Пример преобразования волнового фронта и использования объекта в качестве функционального элемента можно найти еще в классической интерферометрии, где эти операции применялись для увеличения чувствительности. Они осуществлялись за счёт последовательного многократного прохождения зондирующего излучения через исследуемый объект, что приводило к перемножению комплексных амплитуд пропускания объекта и, соответственно, к сложению фаз комплексных амплитуд, необходимому для получения интерферограмм с повышенной чувствительностью. На преобразовании волнового фронта делением его по амплитуде и совмещением затем полученных волновых фронтов с взаимным смещением, поворотом, изменением масштаба или инверсии координат основана сдвиговая интерферометрия.
В топографической интерферометрии диффузно отражающих объектов выбором углов наклона освещающего излучения и направления наблюдения фотографирования ) восстановленного изображения изменялась чувствительность к измерении отдельных проекций вектора перемещения, а пространственная фильтрация объектного волнового фронта использовалась для повышения контраста интерференционных полос и получения изотет (линий равного значения) проекции вектора перемещения, нормальной поверхности объекта. Преобразование волнового фронта, отраженного от объекта за счёт смещения освещающего источника, изменения его длины волны или применения иммерсионной жидкости, лежат в основе голографических методов получения интерференционных контурных карт рельефа поверхности /10/.
Различные преобразования волнового фронта найдя широкое применение и в спекл-интерферометрии, где их применение впервые позволило получать изотеты тангенциальной проекции вектора перемещения с переменной чувствительностью, а также распространить методы сдвиговой интерферометрии и интерференционного сравнения с образцовым объектом на диффузно отражающие объекты.
Рассмотрим более подробно два метода, использующие преобразование волнового фронта, которые нашли применение для анализа
- 9 -
внутренней структур объекта (томография) и его вектора перемещения в тангенциальном направлений.
Томография, как метод исследования внутренних скрытых структур трехмерного объекта, получила в последнее время широкое распространение. Сущность метода состоит в том, что путем соответствующей обработки излучения, прошедшего через объект под различными углами так называема” проекций, получают изображение его поперечного сечения,
Известные топографические системы, использующие оптическое излучение в качестве зондирующего, обладают существенным недостатком, они требуют регистрации составляющих поля и последующей обработки на ЭВМ. Подобная двухэтапная обработка приводит к тому, что возникает разрыв во времени между регистрацией проекций и визуализацией требуемого изображения. Для устранения этого недостатка в /2/ было предложено объединить оба этапа томографического процесса.
При оптическом многоракурсном зондировании проекции представляют собой модуляцию светового поля. Они непосредственно, минуя этап регистрации, поступают на вход томографического процессора. На выходе оптической части устройства формируется изображение сечения объекта - томограмма, В работе /2/ этот одноэтапный процесс прямого измерения локального значения показателя преломления либо его ослабления в сечений объекта предложено называть оптической томографией.
Для фазовых объектов, в сечении которых определяется показатель преломления, фаза прошедшего излучения пропорциональна проекции.
Пусть n(x,у) - распределения показателя преломления в сечении объекта. Плоский монохроматический пучок света, проходя через данное сечение фазового объекта, будет описываться e = a0exp[i2p
Фj/ L
], где L
- длина волны, Фj - интегральный фазовый набег вдоль луча, Фj связан с функцией n(х,y) уравнением Радона:
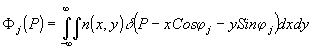 (3) (3)
- 10 -
Здесь p,j
- параметры нормального уравнения прямых зондирования р=хСоsj
+ysinj
. Задача состоит в том .чтобы, зная функции Фj(p ) для всех углов зондирования j
j, из интервала [-p
/2;p
/2] найти n(x,y).
В работе /11/ было предложено осуществлять решение ИУ Радона в процессе многоракурсного многопроходового зондирования. Этот метод решения с последующим представлением n(x,у) в виде интерферограмм получил название топографической интерферометрии, а устройство - томографического интерферометра.
Для решения уравнения (3) в томографическом интерферометре наиболее целесообразно использовать алгоритм обратных проекций, согласно которому распределение показателя преломления в сечении объекта n связано с проекциями Фj(р) уравнением:
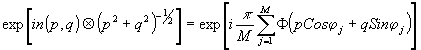 (4) (4)
Операция суммирования обратных проекций описывается показателем экспоненты в правой части выражения (4).
Для вычисления правой части уравнения (4) была разработана оптическая схема многоракурсного многопроходного интерферометра, которая позволила на выходе получить значения показателя преломления в сечении объекта для случая слабоизменяющихся фазовых объектов. Для более сложных случаев в /2/ предложено во пользовать оптическую сие теку со сдвиговым интерферометром в петле обратной связи.
В качестве второго примера рассмотрим принципиальную оптическую схему, показанную на рис.1 и предназначенную для получения изотет (линий равного значения. тангенциальной проекции D
rx вектора перемещения D
r в реальном времени с одновременным устранением спекл-шума на восстановленном изображении /12/.
Диффузно отражающий объект с плоской поверхностью i совещается симметрично нормали к ней двумя коллимированными волновыми полями 2 и 3 и с помощью объектива 4 записывается на голограмму сфокусированного изображения 5 с опорным волновым полем 6. После записи на голограмму исследуемого объекта, находящегося в первоначальном состоянии, опорное волновое поле перекрывают, превращая доступ его к голограмме, а к объекту прикладывают деформирующую
- 11 -
нагрузку. Саму голограмму освещаю” одновременно двумя объектными волновыми полями, распространяющимися в направлении от оптической системы. Восстановленные волновые поля, распространяющиеся по направлению опорного волнового поля при записи голограммы, попадают в блок оптической фильтрации, состоящей из объектива 7 и отверстия 8 в непрозрачном экране. Образующуюся при деформации объекта интерференционную картину наблюдают или фотографируют, фокусируясь в плоскость голограммы через отверстие 8.
В рассмотренной схеме исследуемый объект играет многофункциональную роль. Во-первых, его диффузно отражающая поверхность используется как полупрозрачная пластинка на выхода интерферометра, соединяющая и направляющая по одному пути интерферирующие волновые поля. Во-вторых, коллимированное в симметричное освещение объекта и наблюдение (фотографирование) его по одному направлению позволяют устранить зависимость интерферограммы от изменения углов освещения и наблюдения по поверхности объекта, а также от других проекций (D
ry,D
rz) вектора перемещения, в результате чего полученная интерферограмма практически не нуждается в дальнейшем расчете. Наконец, восстановление голограммы объективными волновыми полями приводит к тому, что восстановленное изображение оказывается пропорциональным распределению не комплексной амплитуды, как обычно, а интенсивности по поверхности объекта.
В связи с этим энергетический спектр, описывающийся по теореме Винера-Хинчина преобразованием Фурье от функции корреляции, в данном случае по интенсивности, содержит в себе d
-функцию, т.е. на одну из его частот приходится 50% анергии. Эта частота пропускается отверстием в непрозрачном экране, что я приводят к устранению спекл-шума на восстановленном изображении.
Приведенные примеры, на наш взгляд, достаточно наглядно иллюстрируют особенности а возможности предложенного авторами подхода к реализации прямых оптических измерений некоторых параметров исследуемых объектов, хочется надеяться, что изложенные принципы найдут более широкое применение при создании измерительных устройств и позволят решить задачу автоматизации оптических исследовании для самых различных областей науки в техники.
- 12 -
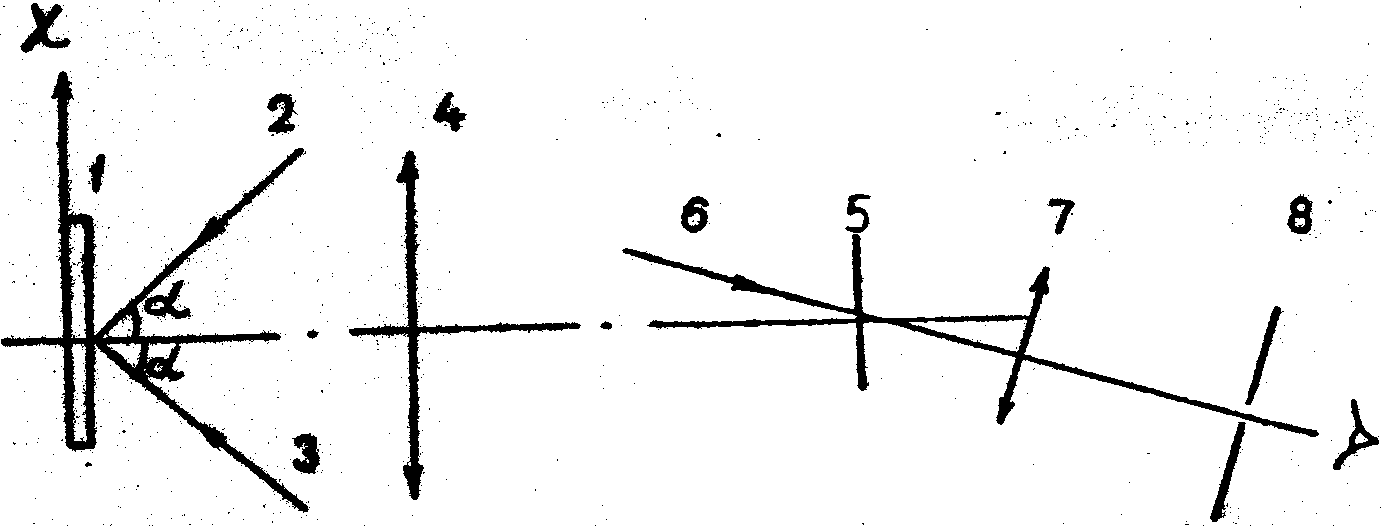
Рис.1.
- 13 -
Литература.
1. Голография. Методы и аппаратура, под ред. В.М.Гинзбург, Б.М.Степанова. - М., Сов.радио, 1974.
2. Г.Н.Вишняков. Г.Г.Левин. В сб. "Физические основы голографии", Л., 1981, с.178-190.
3. П.Я.Белоусов, Ю.Н.Дубнищев, И.Г.Палъчикова. Автометрия. № 3, 1982, с.34-38.
4. Б.С.Ринкевичюс. Лазерная анемометрия, М., Энергия, 1978.
5. Р.У.Шафер, Р.М.Мерсеро, М.А.Ричардс. ТИИЭР, 1981 ,т.69, №4, с.34-55.
6. g.cesini et al. optica acta, 1978, 25, n6, 501-508.
7. А.Л.Ауслендер, Г.Н.Вишняков. Г.Г.Левин. В кн. "Оптическая обработка информации", Л., 1978, с.107-115.
8. d.jablonowsci, s.h.lee, appl.phys., 1975, 8, 51-58.
9. Е.С.Нежевенко, Б.Н.Спектор. Автометрия, 1975, №3, с.98-103.
10. Ч.Вест. "Голографическая интерферометрия", М., Мир, 1982.
11. Г.Н.Вишняков, Г.Г.Левин. Оптика и спектроскопия, 1982, т.52, 5, с.929-932.
12. Н.Г.Власов, С.Г.Галкин, Ю.П.Пресняков, Б.М.Степанов. В сб. Труды Хiv межд. конгресса высокоскоростной фотографии и фотоники, СССР, М., 2980. с.263-264.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

