ОПТИЧЕСКАЯ ТОМОГРАФИЯ

Г.Н.Вишняков, Г.Г.Левин

Большой интерес представляет исследование пространственного распределения оптических неоднородностей (коэффициента поглощения или показателя преломления) объектов по результатам их зондирования излучением оптического диапазона. Сочетание оптического многоракурсного зондирования с последующей оптической обработкой прошедших через объект волновых фронтов, реализующих какой-либо алгоритм восстановления изображения сечения по его проекциям, позволяет в реальном времени исследовать пространственную структуру динамических объектов и процессов. Этот метод исследования предложено называть оптической томографией.

1. Введение

Томография как метод исследования пространственной внутренней структуры объектов по результатам их зондирования проникающим излучением в последнее время получила широкое распространение в различных областях науки, техники и медицины /1,2/. Слово "томография" происходит от двух греческих слов "томос" -сечение и "графия" - отображение. Суть метода заключается в следующем. Исследуемый объект зондируется проникающим излучением с различных стороной прошедшее излучение регистрируется линейкой (или матрицей) дискретных или непрерывных детекторов. Пространственная модуляция прошедшего излучения определяется внутренней структурой объекта, т.е. распределением коэффициента поглощения или показателя преломления для данной длины волны зондирующего излучения. После регистрации набора проекций, полученных с различных направлений, все они совместно обрабатываются

- 179 -

по определенному алгоритму. Результатом обработки является двумерная карта значений коэффициента поглощения или показателя преломления в поперечном сечении исследуемого объекта, представленная в том или ином виде - полутоновые изображения, изолинии и т.д. В зависимости от природы зондирующего излучения различают рентгеновскую, ультразвуковую, ионную и т.п. томографию. Существует еще одна классификация томографических систем в зависимости от типов устройств обработки проекций. Различают компьютерную и аналоговую томографию. В случае компьютерной обработки используют достаточно мощные цифровые вычислительные машины -спецпроцессоры, работающие по жесткой программе /1/. При использовании аналоговой техники анализ проекций производится, как правило, в оптико-электронных процессорах (ОЭП), работающих с меньшей точностью, но обладающих большим быстродействием и, как ни странно, гибкостью при реализации алгоритма обращения /3,4/.

Большой интерес представляет исследование пространственного распределения оптических неоднородностей объекта. Нетрудно заметить, что сочетание оптического зондирования с последующей оптической обработкой волнового фронта сулит наибольшие перспективы при оперативной диагностике амплитудно-фазовых объектов и процессов. Этот метод исследования мы и будем в дальнейшем называть оптической томографией.

2. Математические основы томографии

Пусть функция ¦ (x,y) характеризует пространственное распределение оптических неоднородностей в выделенном поперечном сечении (х,у) объекта и пусть ¦ (х,у) = 0 вне круга радиуса Р₀. Для поглощающих (амплитудных) объектов ¦ (х,у) пропорциональна коэффициенту, поглощения a (х,у) для определенной длины волны зондирующего излучения l , т.е. ¦ (х,у) = Р_0l (x,y). Для фазовых объектов ¦ (х,у)=Р₀[n(х,у) – n₀]/l , где n(х,у) и n₀ - показатели преломления, соответственно, исследуемого объекта и окружающей среды. При зондировании объекта пучком параллельных лучей, без учета рефракции, т.е. в линейном приближении, интегральная выходная характеристика зондирующего

- 180 -

излучения Ф(з,y ), называемая проекцией объекта в направлении y , связана с функцией ¦ (x,у) преобразованием Радона

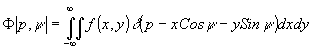(1)

где -¥ < p < ¥ , 0 £ y £ p и | p| , y - параметры нормального уравнения прямых зондирования (рис.1). Заметим, что в (1) все пространственные координаты безразмерны (отнормированы на Р₀). Таким образом, необходимо по набору экспериментальных данных о проекциях Ф(р,y _j) .полученных при различных углах зондирования y _j, восстановить функцию ¦ (x,у), описывающую искомую томограмму. Рассмотрим некоторые основные алгоритмы решения уравнении Радона (1).

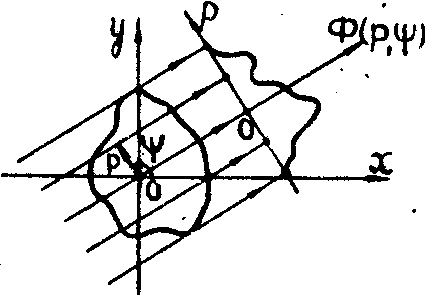
Рис.1.

а) Алгоритм Фурье-синтеза

Применяя к обеим частям уравнения (1) одномерное преобразование Фурье по координате р, находим

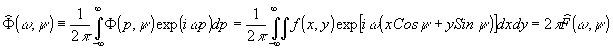(2)

Это утверждение носит название теоремы о "центральном слое". В (2) функция 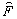(w ,y ) есть двумерный Фурье-спектр функции ¦ (х,у), записанный в полярной системе координат. Из (2) следует

- 181 -

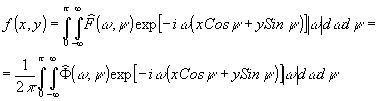(3)

т.е. для восстановления ¦ (x,у) необходимо взять 2-мерное обратное преобразование ирье от синтезированного по экспериментальным данным спектра 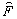(w ,y ).

б) Алгоритм фильтрации обратных проекций

Пусть q º xСosy + уsiny , перепишем (3) в виде

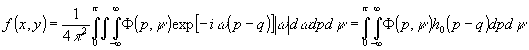(4)

где

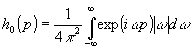, (5) – фильтрующая функция.

Видно, что в (5) интеграл по w расходится, в чем и проявляется некорректность уравнения (1), которое является интегральным уравнением 1-го рода. Для регуляризации этой задачи в интеграл (5) вводят аподизирующую четную функцию А(w ), ограничивающую интеграл по w , т.е. переходят к фильтрующей функции h(р) вида

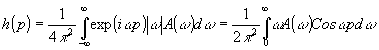(6)

Тогда (4) можно переписать в виде

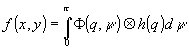(7)

где Ä - значок свертки.

Функция Ф(q,y ) º Ф(xcosy + ysiny ) называется обратной проекцией и образуется из одномерной проекции Ф(p,y ) путем ее равномерного растяжения по направлению, перпендикулярному оси р. Таким образом, из (7) следует, что для восстановления ¦ (x,у) необходимо просуммировать но углу отфильтрованные обратные проекции.

Так как при восстановлении ¦ (x,у) по ее проекциям используются

- 182 -

линейные операции, то этот процесс можно характеризовать импульсным откликом р(х,у),связывающим входную идеальную функцию ¦ _ид(x',у'), из которой образуются проекции, и восстановленную функцию ¦ (х,у):

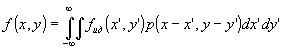(8)

Найдем вид импульсного отклика р(х,у). Для этого, подставив в (7) выражение для проекции (1) и поменяв порядок интегрирования, получим

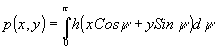(9)

Подставив в (9) определение фильтрующей функции (6), найдем другое выражение для импульсного отклика;

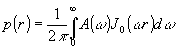
Ясно, что для наилучшего восстановления ¦ (х,у) по ее проекциям необходимо так подобрать фильтрующую h(p) или аподизирующую А(w ) функции, чтобы импульсный отклик р(х,у) был близок к d -функции.

Рассмотрим два примера. Если в выражении (7) не осуществлять операцию фильтрации обратных проекций, т.е. когда h(p) º d (q), то из (9) следует, что в этом случае импульсный отклик р(г) ~ 1/r и восстановленная функция оказывается сверткой искомой функции с функцией вида 1/r. Если выбрать аподизирующую функцию А(w ) в виде прямоугольного окна А(w ) = rect(w /2w _m), то импульсный отклик p(r) = 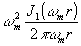соответствует отклику дифракционно-ограниченной оптической системы с крупным зрачком.

в) Инверсное преобразование Радона

Пользуясь тождеством |w | º w ·sgnw , где sgn(w ) - знаковая функция, выражение (3) можно переписать в виде

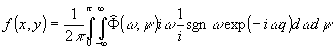(10)

- 183 -

Так как 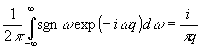/3/, то, используя теорему о преобразовании Фурье от свертки и производной функции, из (10) следует

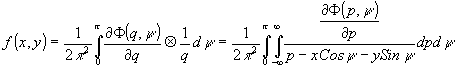(11)

Формула (11) называется инверсным преобразованием Радона. Внутренний интеграл в (11) берется в смысле главного значения.

3. Оптическая томография поглощающих объектов

При исследовании оптических характеристик объекта томографическими методами зондирование производится оптическим излучением. При этом амплитудная составляющая поля, прошедшего через объект, позволяет определять коэффициент поглощения объекта, а фазовая - показатель преломления. Исследование самосветящихся объектов и процессов также возможно по анализу амплитудной составляющей поля собственного излучения на определенной частоте /5/.

Анализ алгоритмов, приведенных в предыдущем разделе, показывает, что практически все они могут быть реализованы в ОЭП при исследовании коэффициента поглощения объекта (см., например, /4/).

Согласно выражениям (2), (3) для реализации алгоритма Фурье-синтеза необходимо выполнить следующие операции:

1) одномерное преобразование Фурье от каждой проекции; 2) повернуть каждый спектр на определенный угол; 3) накопить все спектры; 4) умножить полученный спектр на фильтр с пропусканием |w |; 5) выполнить обратное двумерное преобразование Фурье. В случае малого числа проекций необходимо также реализовать оптическую аппроксимацию двумерного спектра.

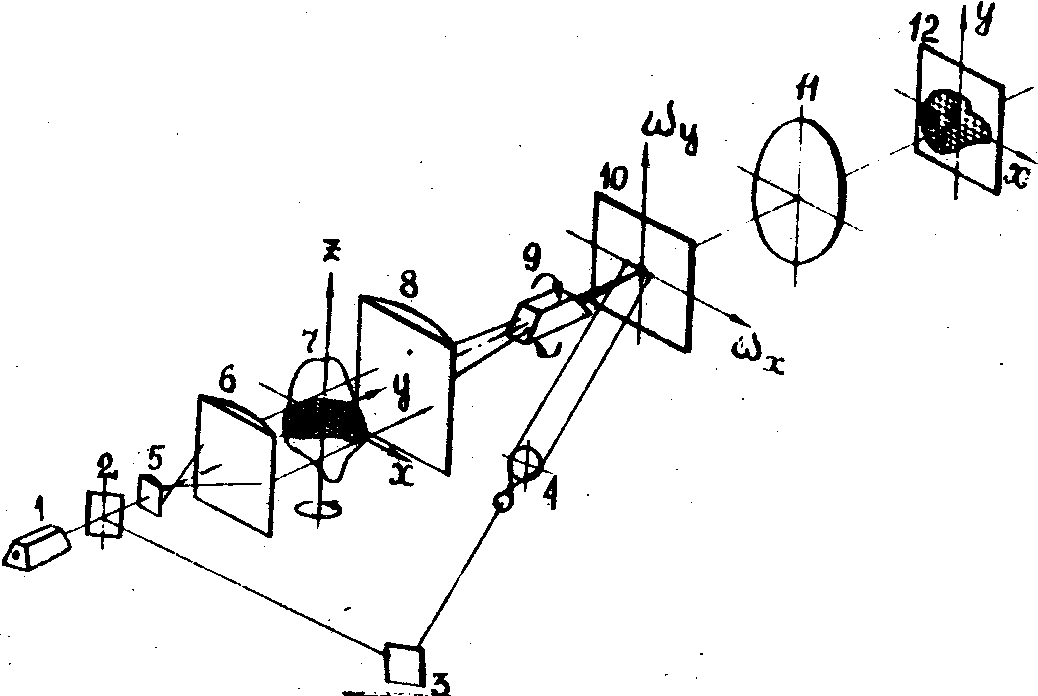
На рис.2а изображена принципиальная схема когерентно-оптического процессора, последовательно выполняющего все требуемые операции /6/:

1) одномерное преобразование Фурье выполняется цилиндрической линзой 8; 2) поворот спектров - призмой Дове 9; 3) на регистраторе 10 осуществляется голографическая запись набора

- 184 -

одномерных спектров к умножение их на частотный фильтр с пропусканием | w | ; 4) объектив 11 выполняет обратное двумерное преобразование Фурье. На рис.2б представлена фотография поперечного сечения тест-объекта, состоящего из 4-х цилиндрических непрозрачных стержней, расположенных в вершинах квадрата размером 10х10 мм², восстановленного в оптическом процессоре по 4-м проекциям. Отметим, что при исследовании динамических объектов необходимо использование многоракурсной схемы просвечивания, в каждом канале которой строится оптическая схема, аналогичная схеме на рис.2а. При восстановлении поперечного сечения объекта по малому числу проекций частотная плоскость заполняется неполностью, что приводит к уменьшению отношения сигнал-шум в восстановленном сечении. Для устранения этого, а также для повышения надежности восстановления необходимо заполнить всю частотную плоскость, имея информацию о спектрах ограниченного числа проекций, т.е. реализовать тот или иной тип .оптической аппроксимации заданных спектров проекций.

а)

б)

Рис.2.

- 185 -

4. Томографическая интерферометрия фазовых объектов

Большой интерес представляет исследование пространственного распределения показателя преломления фазового объекта по результатам его оптического зондирования. Известные методы определения показателя преломления в сечении фазового объекта обычно используют многоракурсные схемы просвечивания объекта оптическим излучением и запись интерферограмм объекта для каждого ракурса. По набору полученных интерферограмм путем измерения отклонения интерференционных полос получают информацию о функции изменения оптической длины пути зондирующих лучей, которая связана с искомым распределением показателя преломления преобразованием Радона. Для получения искомого пространственного распределения необходимо ввести измеренные данные в ЭВМ, решить указанное уравнение Радона и отобразить ответ в виде, удобном для оператора /7/. Существует достаточно большой круг задач, например, неразрушающий контроль качества изготовления стекловолокна, оперативный анализ плазменных, аэро- и гидродинамических процессов и т.д., для которых необходимо получать информацию о пространственном распределении показателя преломления в реальном времени и удобном, наглядном виде.

В настоящем разделе описана схема оптического процессора, позволяющего восстанавливать пространственное распределение показателя преломления в поперечном сечении фазового объекта в реальном времени. Этот процессор можно назвать томографическим интерферометром, т.к. в нем информация о распределении показателя преломления в сечении объекта заключена в виде карты интерференционных полос, которая является одновременно картой линий равных значений показателя преломления. Работа процессора основана на аналоговой оптической реализации алгоритма фильтрации обратных проекций.

Как показано в разделе 2, если не выполнять операцию фильтрации, то для восстановления ¦ (x,у) необходимо просуммировать повернутые обратные проекции. Однако, в этом случае восстановленная функция оказывается несколько искаженной ("размытой") операцией свертки с функцией вида 1/r. Но для низкочастотных

- 186 -

функций ¦ (x, у), которые, как правило, исследуются в интерферометрии при малом числе ракурсов просвечивания, этим сглаживанием искомого распределения можно пренебречь.

Оптическая схема процессора - томографического интерферометра - приведена на рис.3 (изображена 3^х ракурсная схема просвечивания). В этом интерферометре исследуются объекты с постоянным или планоменяющимся вдоль оси z показателем преломления. Для зондирования объекта 6 используется плоский волновой фронт А₀(p,z) = const, волновой вектор которого перпендикулярен z. Нетрудно заметить, что в данной оптической схеме выполняются все операции, требуемые для получения функции ¦ (х,у): растягивание проекций Ф(p,y _j) вдоль оси, параллельной оси р, достигается автоматически за счет коаксиальной симметрии объекта; поворот на угол y _j выполняется призмами Дове 8, 11; суммирование обратных проекций обеспечивается многократным проходом волнового фронта через объект. В результате после М проходов (на рис.3 М = 3) зондирующий волновой фронт можно описать выражением:

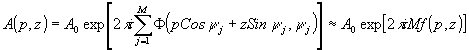(12)

которое уже содержит информацию о показателе преломления в виде фазовой модуляции зондирующего волнового фронта. Для визуализации подученного фазового распределения можно, например, зарегистрировать голографическую интерферограмму 13, уравнение которой в полосах бесконечной ширины запишется в виде:

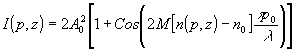(13)

где i(р,z) - интенсивность восстановленного с интерферограммы волнового поля. Из выражения (13) следует, что искомая информация о пространственном распределении показателя преломления в поперечном сечении фазового объекта заключена в виде системы интерференционных полос, которая одновременно является картой линий равных значений показателя преломления, причем при переходе от одной линии к другой значение показателя преломления изменяется на величину l /mp₀.

- 187 -

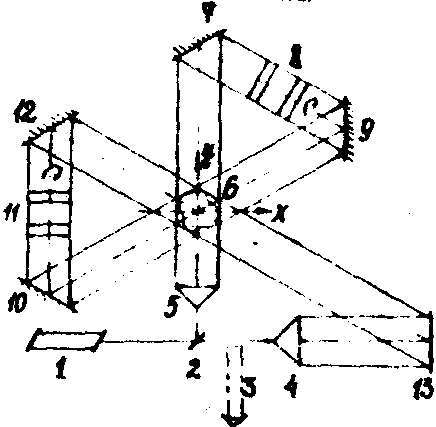
Рис.3.

Описанный выше (рис.3) трехракурсный топографический интерферометр был использован для исследования пространственной структуры тепловых конвекционных потоков, инициированных электрическим нагревом нихромовой проволочки, расположенной вертикально.

На рис.4 приведена фотография восстановленной интерферограммы поперечного сечения (плоскости х,у) конвекционного потока. Из-за дифракции света на проволочке на фотографии отсутствует ее четкая теневая картина. Направления этой проволочки на рис.4 изображены стрелками. На фотографии видна система замкнутых концентрических полос, смещенных относительно центра интерферограммы из-за горизонтального ("бокового") движения нагретого воздуха. При увеличении числа направлений зондирования оставшиеся интерференционные полосы также замкнуты. Правило нахождения количества проекций (ракурсов), необходимых для точного восстановления изображения поперечного сечения, в нашем случае "фазового" изображения показателя преломления в сечении объекта. приведена в /8/. Предложенная схема томографического интерферометра была также смоделирована для измерения профиля показателя преломления в поперечном сечении градиентного стекловолокна. Вместо 3х-ракурсной схемы была использована обычная одноракурсная схема интерференционного микроскопа, но в качестве объекта исследовались три участка одного и тот же стекловолокна, окрещенные под углами в 60°. На рис.5 представлены восстановленные

- 188 -

Рис.4.

Рис.5.

в полосах бесконечной ширины интерферограммы такого объекта. Интерференционные полосы в области пересечения волоков в некотором приближении представляют линии равных значений показателя преломления в поперечном сечении стекловолокна.

В описанном топографическом интерферометре полученные интерферограммы лишь с точностью до операции свертки с функцией типа 1/r определяют искомое распределение показателя преломления. Дня более точного восстановления ¦ (x,у) предлагается продифференцировать по радиусу полученный в томографическом интерферометре волновой фронт (12) с помощью интерферометра радиального сдвига. Тогда волновой фронт, прошедший через томографический

- 189 -

интерферометр и интерферометр радиального сдвига несет информацию уже о более точном распределении показателя преломления в поперечном сечении.

При исследовании 3х-мерных объектов (без коаксиальной симметрии) для перемножения волновых фронтов, необходимого при операции (12), можно использовать высококонтрастные регистраторы голограмм, причем коэффициент контрастности должен быть порядка 2М, где М - число проекций. Отметим, что описанная схема томографического интерферометра может быть также использована для исследования амплитудных и амплитудно-фазовых объектов, причем информация о коэффициенте поглощения будет заключена в виде полутонового изображения.

5. Заключение

Рассмотренные томографические методы оптической диагностики амплитудно-фазовых объектов открывают новые возможности по определению их пространственной внутренней структуры. Бесконтактные прямые измерения коэффициентов поглощения и преломления в поперечном сечении объекта позволяют решить задачи диагностики динамических объектов в процессов в реальном времени. Оптическая томография, в том числе интерферометрическая, основывается на достижениях в области создания оптических процессоров и элементной базы к ним, а также на богатом опыте голографической интерферометрии. Это позволило уже в первых экспериментах получить обнадеживающие результаты при исследовании различиях объектов и процессов.

В заключение авторы выражают благодарность Н.Г.Власову за полезные обсуждения.

Литература

1. А.С.Кэк. ТИИЭР, т.67, стр.79, 1979.

2. Р.К.Мюллер, М.Кавех, Г.Уэйд. ТИИЭР, т.67, стр.146, 1979.

3. Х.Х.Баррет, У.Суинделл. ТИИЭР, т.65, стр.107, 1977.

4. a.f.gmitro et al. opt. engineering, v.19, р.260, 1980.

- 190 -

5. В.В.Пикалов. В кн.: Инверсия Абеля и ее обобщения. Новосибирск, стр.25, 1978.

6. А.Л.Ауслендер, Г.Н.Вишняков, Г.Г.Левин. Опт. и спектр, т.49, стр.946, 1980.

7. Ю.П.Пресняков. Опт. и спектр., т.40, стр.124, 1976.

8. А.Л.Ауслендер, Г.Н.Вишняков, Г.Г.Левин. Опт. и спектр., т.50, стр.408, 1981.