ПРОБЛЕМЫ УПРАВЛЕНИЯ В АДАПТИВНОЙ ОПТИКЕ

М.А.Воронцов

Рассматривается общий подход к вопросам построения систем адаптивной оптики. Основное внимание уделено системам адаптивной фокусировки излучения. Дается сравнительный анализ методов управления фазовым фронтом излученной волны и практические схемы их реализации.

Термин "адаптивная оптика" появился сравнительно недавно, хотя оптические системы с элементами адаптации успешно используются на протяжении 15-20 лет. Повышенный интерес к предмету вызвало появление ряда статей в тематическом сборнике, составленном Д.Фридом /1/ и обзора Дж.Харди /2/, под названием "Активная оптика", посвященного элементной базе адаптивной оптики. После этих публикаций сообщения по адаптивной оптике стали все чаще включаться в программы конференций, симпозиумов и шкод по оптической тематике. Другим импульсом, пробудившим интерес к адаптивным системам явилось открытие явления обращения волнового фронта и последовавшая за этим целая серия работ с обсуждением возможностей использования этого явления в системах адаптивной оптики /3,4/. Что же подразумевается в оптике под термином "адаптивные системы"? Можно дать следующее определение, основанное на практике использования этого понятия в периодических изданиях по оптической тематике. Адаптивными называются оптические системы, элементы которых автоматически подстраиваются под изменяющиеся внешние условия. Простейшими и, пожалуй, самыми первыми примерами адаптивных оптических систем являются следящие интерферометры и системы стабилизации частоты лазера /5,6/. На рис.1 изображена блок схема следящего интерферометра, предназначенного для автоматической компенсации разности хода интерферирующих

- 163 -

лучей. Коррекция разности хода осуществляется с помощью опорного зеркала (1), укрепленного на электромеханическом приводе (2). К приводу с регулятора (3) подводится управляющее напряжение. Сигналом ошибки служит текущее изменение положения интерференционной полосы, регистрируемое фотодетектором(4)

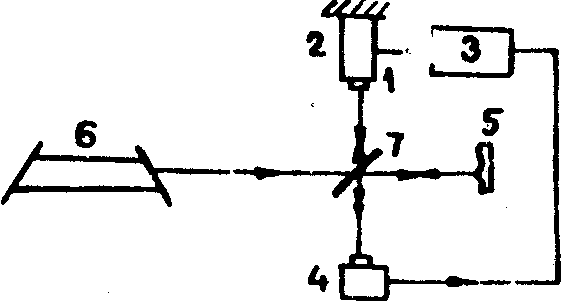
Рис.1. Схема следящего интерферометра Майкельсона:

1 - опорное зеркало; 2 - привод опорного зеркала; 3 - сервосистема; 4 - детектор; 5 - исследуемый объект; 6 - источник; 7 - делительное зеркало.

Такого рода системы назывались системами автоматической юстировки, хотя полностью укладываются в рамки определения адаптивных оптических систем. Приведенное выше определение адаптивных систем, по-видимому, не устроило бы математиков и инженеров-специалистов по адаптации и облучению в автоматических системах. Эта область теории автоматического управления гораздо старше по возрасту адаптивной оптики и в настоящее время обладает . мощным аппаратом идей и математических методов. По определению Я.З.Цыпкина /7/, адаптивные системы - это системы, уменьшающие первоначальную неопределенность на основе информация, получаемой в процессе управления. Чтобы разобраться с терминологией, полезно кратко остановиться на истории развития теории автоматического регулирования /7/. В ней можно выделить три этапа: детерминизма, стохастичности и адаптивности. В период детерминизма возможно полное математическое описание системы: известны уравнения динамики системы, полностью измеримы внешние воздействия. Во второй период стохастичности известными предполагаются лишь статистические характеристики возмущавших внешних воздействий. В

- 164 -

период адаптивности, продолжающейся и в настоящее время, неопределена как структура системы регулирования, так и статистические характеристики внешних воздействий. Все это затрудняет управление системами, но не делает его невозможным. Для управления необходимы адаптация и обучение, которые уменьшают первоначальную неопределенность. Современная адаптивная оптика переживает счастливое время детерминизма и только начинает вступать в период стохастичности и адаптации, как она понимается в теории управления. Существующие адаптивные оптические системы более правильно следовало бы назвать многоканальными системами автоматического регулирования, однако, термин "адаптивная оптика" можно считать устоявшимся, кроме того, есть надежда на адекватное отражение содержания термина в недалеком будущем.

Основные типы адаптивных оптических систем

Первые задачи, для решения которых были созданы многопараметрические адаптивные оптические системы связаны с компенсацией фазовых искажений, вносимых атмосферной турбулентностью, при наблюдении астрономических объектов через атмосферу. Эти системы получили в дальнейшем название адаптивных телескопов /8/ или систем с принимаемой волной.

Возможности использования адаптивной оптики в астрономии не ограничиваются лишь борьбой с вредным влиянием атмосферной турбулентности. С помощью адаптивной техники компенсируют и всевозможные искажения волнового фронта в самой системе, связанные, например, с вибрациями и термическими расширениями элементов.

В последнее время широкое распространение получили адаптивные оптические системы о излученной волной. Сфера применения систем этого типа продолжает непрерывно расширяться. Помимо традиционной для адаптивной оптики задачи компенсации искажений, вносимых в излученную волну турбулентной атмосферой, выполнен ряд работ по компенсации адаптивными системами оптических неоднородностей в активной среде оптических генераторов и усилителей /9/. Обсуждаются возможности подавления нелинейных оптических эффектов при распространении излучения в условиях теплового

- 165 -

самовоздействия /10/.

Общая структура адаптивных оптических систем определяется той целью, ряди которой вводится адаптация. В дальнейшем в основном будут рассматриваться системы с излученной волной, пред назначенные для аффективной передачи (фокусировки) излучения через оптически неоднородную среду. Область применения таких систем весьма широка: оптическая связь со спутниками, задачи лазерной локации, лазерная сварка и резка металлов, лазерный термоядерный синтез и др. Введение адаптации в таких системах преследует цель наилучшим образом сфокусировать излучение на мишень.

При стремлении достигнуть этой цели возникают три задачи: выбор цели, согласование ее с имеющимися возможностями и способы достижения цели.

1. Выбор и точная формулировка цели. Последнее предполагает введение некоторой числовой характеристики (критерия качества), по значению которой мотаю судить о степени достижения пели. Нередка ситуация, когда мы знаем, что хотим, но затрудняемся в выборе критерия качества. Например, задачу фокусировки излучения можно сформулировать как задачу компенсации влияния оптических неоднородностей среды, однако в такой постановке задача может не иметь решения, так как фазовые искажения далеко не всегда моуно полностью скомпенсировать.

2. Согласование цели с имеющимися ресурсами и ограничениями. В адаптивных системах фокусировки излучения следует отметить прежде всего ограниченные возможности получения или измерения текущей информации. Пусть цель управления сформулирована в форме некоторой оценки (критерия) качества фокусировки

; = {x,y}

где r () - область мишени, в пределах которой требуется сконцентрировать излучение; e(,z₀,t) - комплексная амплитуда поля в плоскости объекта фокусировки. При r () = d ( - ₀) целью управления является максимизация пиковой интенсивности в точке (₀,z₀). Для организации процесса максимизации критерия j₁ необходимо иметь возможность измерять пространственное

- 166 -

распределение интенсивности i = Еe^* в пределах r (). В адаптивных системах с несогласованной мишенью (лазерные локаторы и др.) этого сделать нельзя. Измерению доступна лишь информация о рассеянном объектом поле y (,z,t) в пределах приемной апертуры, расположенной в некоторой плоскости z=0. Ограниченные возможности получения необходимой информации приводят в рассмотренном примере к необходимости отказаться от критерия j₁, хотя с физической точки зрения он может адекватно отражать наши желания. Ограниченные возможности измерения заставляют идти на компромисс и переформулировать саму постановку задачи. Необходимо выбирать критерий, согласованный с имеющимися возможностями измерения. Он должен, с одной стороны, зависеть лишь от измеряемых величин, а с другой, - отражать цель, ради которой вводится адаптация. Это противоречие между желаемым и техническими возможностями далеко не всегда разрешимо. Приведем ряд примеров. Если мишень точечная, то в качестве критерия фокусировки можно взять интеграл от интенсивности рассеянного поля в плоскости детектора

j_r = ò m()| y (,z₀=0,t)| ²d² (1)

(критерий резкости). Интенсивность | y | ² пределах m() легко измеряется некогерентным детектором. Концентрация поля на точечной мишени вызывает увеличение амплитуды рассеянной волны y и, следовательно, возрастание критерия резкости. Для неточечного объекта поле y , а значит, и j_r сложным образом зависят от формы и структуры поверхности объектами максимизация j_r может не привести к фокусировке излучения /11/. Приведем ряд других критериев фокусировки

j_n = ò m()| y | ⁿd² (2)

(Этот критерий является обобщением (1)).

j_И = ò | e| | y | cos(u + j )| _{z = 0}d² (3)

В интерференционном критерии (3) u = u(, z = 0, t) - фаза излученной волны; j =j (, z = 0, t) - фазовой профиль рассеянного поля y ).

- 167 -

В /12/ введены статистические критерии, основанные на анализе спектральных характеристик рассеянного поля, например, дисперсия s ² фототока, полученная при регистрации рассеянного поля. От выбранного критерия во многом зависит структура и эффективность работы всей адаптивной системы. Для оценки возможностей критерия отражать цель адаптации необходимо найти соответствие критерия, измеренного в плоскости приемной апертуры с некоторой характеристикой излучения в плоскости мишени. Такую связь можно записать аналитически далеко не всегда. Для критерия резкости (1), интерференционного критерия j_И и s ², в частности, имеем;

j_r ~ j₁, при r = d ( - ₀), j_И = reò e^{2c |} _z0d², s ² = ò i^2| _z0d²

где c = c () - коэффициент рассеяния поверхности объекта. Другое, не менее важное ограничение, которое необходимо учитывать в каждой постановке задачи адаптивной фокусировки, связано с техническими возможностями корректоров фазового фронта излученной волны.

Результатом работы сервосистемы является формирование волнового фронта излученной волны, который можно представить в следующей форме u(,t)=.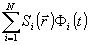

Важнейшей характеристикой корректора является число n степеней свободы или независимых управляющих воздействий Ф_i(t). Каждый управляющий сигнал Ф_i, вызывает некоторую деформацию ~ s_i() волнового фронта. В современных адаптивных системах фокусировки число n каналов управления может достигать нескольких десятков /2/. Возрастание n, как правило, приводит к увеличению предельного значения j° критерия качества, которое может быть, в принципе, достигнуто. Важно знать, как зависит предельное значение j° от n и какой выигрыш дает введение каждой новой степени свободы. Такой анализ для приемных адаптивных систем проведен в /13/. Вид функций влияния (определяется типом корректора. С конкретизацией корректора волнового фронта, используемого в адаптивной системе, связано представление критерия качества j в виде функции переменных управления Ф_i и некоторых параметров среды 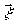; j = j(Ф₁,... Ф_i,... Ф_n) Эту зависимость j от {Ф_i} часто называют дискриминаторной характеристикой.

- 168 -

При каждом фиксированном значен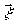ии дискриминаторная характеристика имеет экстремум, соответствующий наилучшей степени фокусировки, достижимой для данного корректора и выбранной оценки качества фокусировки. Результатом работы адаптивной системы является достижение этого экстремума и его текущее отслеживание при изменении внешних воздействий .

3. Способы достижения цели.

Поиск экстремума функций многих переменных является сложной математической проблемой /14/. В адаптивной оптике дело осложняется тем, что поиск экстремума необходимо производить достаточно быстро, например, в случае атмосферных задач за времена порядка 10^-2 ¸ 10^-3 с. (время замороженности оптических неоднородностей). В противном случае вид оптимизируемой функции будет меняться в процессе поиска экстремума. Кроме того, при выборе того или иного алгоритма оптимизации следует учитывать трудности технического характера, с которыми придется столкнуться при его реализации.

Алгоритмы управления в адаптивной оптике

К настоящему времени разработано и исследовано большое число методов оптимизации функций многих переменных. Пожалуй наиболее известными являются градиентные алгоритмы. В существующих адаптивных системах для поиска экстремума критерия практически используются именно градиентные методы или, как их иногда называют в иностранной литературе, методы восхождения на холм. Любой градиентный метод заключается в построении последовательности управляющих воздействий {Ф^(к)_i} по правилу

Ф^{(к +1)}_i = Ф^(к)_i - a _ij'_i(Ф^(к)_i, … Ф^(к)_n), a ^(к)_i > 0, к = 0, 1, 2 … (4)

В (4) {j'_i} - градиент критерия качества j на к-ом шаге итерационного процесса оптимизации. Градиентный метод (4), как и все итерационные методы, предполагает выбор начального приближения {Ф⁽⁰⁾_i} (исходного состояния корректора волнового фронта). Числа {a ^(к)_i} - называют длиной шага градиентного метода. Существуют

- 169 -

различные способы выбора величин a ^(к)_i в (4). В зависимости от этого можно получить различные варианты градиентного метода. Для существующих адаптивных оптических систем характерно использование не дискретных градиентных алгоритмов поиска экстремума, а их непрерывных аналогов. Они получаются посредством предельного перехода от разностных уравнений (4) к непрерывным путем замены дискретного шага "к" непрерывным временем t. Простейшим таким аналогом (4) является система уравнении первого порядка

dФ_i/dt = a _i(t)j'(Ф₁, ... Ф_n) (5)

функции a _i(t) играют роль коэффициентов усиления в каналах сервосистемы. Хотя дискретные алгоритмы (4) являются наиболее распространенными (в силу удобства использования на ЭЭЛ), в адаптивных системах их реализация связана с рядом трудностей. Дело в том, что корректоры волнового фронта, например, адаптивные зеркала инерционны. Такое зеркало невозможно заставить мгновенно изменить свой профиль при переходе к очередному шагу градиентного метода или сохранить его за время между последовательными итерациями. Таким образом, структура корректора накладывает определенные ограничения на возможность использования того или иного алгоритма управления. Динамику корректора можно учесть, если использовать непрерывные алгоритмы оптимизации более высокого порядка.

Рассмотрим адаптивное зеркало, составленное из отдельных сегментов. Каждый сегмент управляется своим приводом, динамика которого описывается уравнением колебаний математического маятника.' В адаптивных системах с таким корректором возможно использование лишь непрерывных алгоритмов второго порядка, типа

c_id²Ф_i/dt² + d _idФ_i/dt + b _iФ_i (6)

где с_i, d _i, b _i - некоторые неотрицательные коэффициенты. Этому непрерывному алгоритму соответствует многошаговый дискретный аналог. В ряде случае алгоритм (6) может оказаться более эффективным по сравнению с (5), так как в силу присущей ему

- 170 -

инерционности он позволит проскочить небольшие локальные экстремумы. При c_i=0 и d _i = 1 получим алгоритмы оптимизации первого порядка.

Какой бы из описанных выше методов поиска экстремума не был выбран для его реализации, в адаптивной системе необходимо выделить градиенты j'_i оптимизируемого критерия j по переменным управления Ф_i. С этой целью в волновой фронт излученной волны вводятся пробные вариации и измеряются соответствующие им малые изменения критерия, пропорциональные искомым градиентам. Этот способ выделения градиентов известен как метод апертурного зондирования. Пробные движения в каждом канале управления могут быть введены как последовательно, так и одновременно сразу во всех каналах. В последнем случае пробные движения представляют собой гармонические сигналы a_i·sin(w _i·t) малой амплитуды a_i, которые добавляются к сигналам управления Ф_i. В каждом канале управления пробные сигналы вводятся со своей частотой. Это позволяет идентифицировать соответствующие им вариации критерия. Рис.2 иллюстрирует принцип выделения градиента в методе апертурного зондирования. На рис.2 изображена условная зависимость некоторого критерия фокусировки j от переменной управления Ф_i. Сигналы сканирования по Ф_i а) и б) вызывают модуляцию критерия; сигналы в) и г). Фаза промодулированного сигнала несет информацию о знаке градиента, а его амплитуда пропорциональна модулю градиента. Принципиальная схема выделения градиентов в методе апертурного зондирования показана на рис.3. В адаптивных системах с мощной излученной волной и большим числом каналов управления выделение градиентов с помощью метода апертурного зондирования является сложной технической задачей. В связи с этим важное значение имеют вопросы получения градиентов критерия без непосредственного введения вариаций в фазовый фронт. Оказывается, такая возможность имеется. Пробными вариациями служит текущее изменение фазы излученной волны. Интересно отметить, что метод обращения волнового фронта модно рассматривать как градиентный метод оптимизации интерференционного критерия (3) /15/. Такой подход позволяет надеяться на создание оптически управляемых адаптивных систем, имеющих практически неограниченное число степеней свободы. На рис.4 приведена одна из возможных схем

- 171 -

адаптивных систем такого рода.

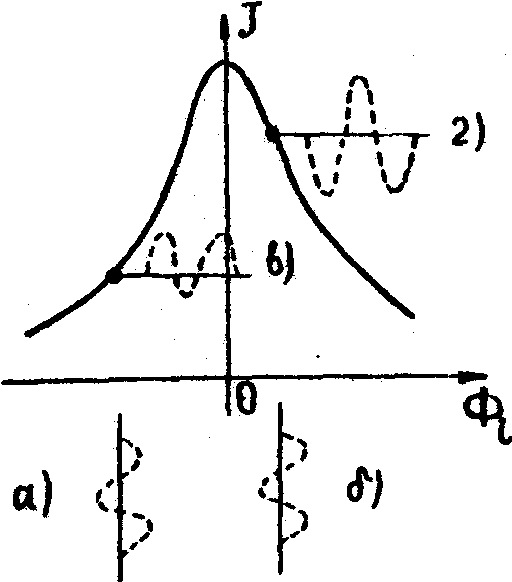
Рис.2. Зависимость критерия фокусировки j от параметра управления Ф_i (в условных единицах):

а) и б) - гармонические сигналы сканирования для двух различных состояний системы;

в) и г) - соответствующие сигналы на выходе детектора.

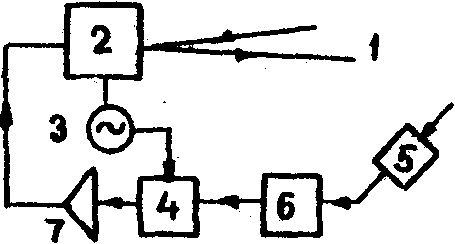
Рис.3. Схема реализации метода апертурного зондирования (показан один канал управления):

1 - излученная волна; 2 - корректор волнового фронта; 3 - генератор опорного напряжения (напряжения сканирования); 4 - фазовый детектор; 5 - детектор; 6 - фильтр; 7 - усилитель.

Корректором волнового фронта является оптически управляемый транспарант (5). Для организации управления таким транспарантом необходимо уметь формировать оптический сигнал, пространственное распределение амплитуды которого пропорционально градиенту функционала j. В /16/ найдено выражение для градиента, зависящее

- 172 -

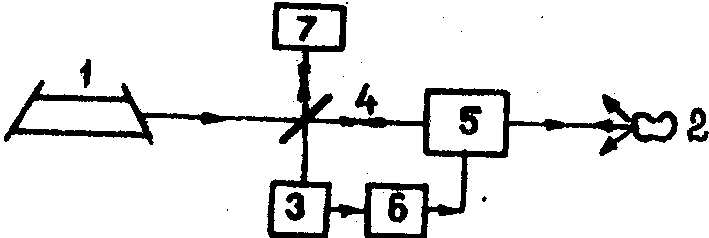
Рис.4. Интерферометрическая схема выделения сигналов управления:

1 - источник; 2 - объект фокусировки; 3 - фотоприемное устройство; 4 - делительное зеркало; 5 - корректор; 6 - регулятор; 7 - система сканирования.

от амплитудного и фазового фронта рассеянного поля y . Выделять градиент можно с помощью изображенной на рис.4 интерферометрической схемы. Перспективным представляется использование для этой цели и методов корреляционной фильтрации /17/.

Литература

1. Адаптивная оптика, сб. статей, М., "Мир", 1980.

2. Дж.Харди, ТИИЭР, № 6, 31, 1978.

3. Б.Я.Зельдович, В.И.Поповичев и др. Письма в ЖЭТФ, 15, 160, 1972.

4. a.yariv., opt. comm., 21, 49, 1977.

5. В.И.Шмальгаузен, УФН, т.132, № 4, 579, 1980.

6. Г.В.Галутва, А.И.Рязанцев. Селекция типов колебаний и стабилизация частоты оптических квантовых генераторов. "Связь", М., 1972.

7. Я.З.Цыпкин. Адаптация и обучение в автоматических системах, "Наука", М., 1968.

8. Космическая оптика. Труды ix Международного конгресса Международной комиссии по оптике, М., "Машиностроение", 1980.

9. j.b.shellan, d.a.holms at all. applied opt., v.19, n 4, 610, 1980.

- 173 -

10. С.А.Ахманов, М.А.Воронцов и др. Изв.ВУЗОВ, "Радиофизика", т.xxiii, № 1, 1, 1980.

11. j.e.pearson, s.a.kokovowski, m.e.pedinofl, j.o.s.a. v.66, n 11, 1261, 1976.

12. М.А.Воронцов, В.И.Шмальгаузен. Квантовая электроника, 7, №.3, 500, 1980.

13. r.j.noll, j.o.s.a, v.66, n 3, 207, 1976.

14. Ф.П.Васильев. Численные методы решения экстремальных задач, М., "Наука", 1980.

15. М.А.Воронцов. В сб. "Физические основы голографии", Материалы xi Всесоюзной школы по голографии и когерентной оптике, Л., 65, 1979.

16. М.А.Воронцов, В.И.Шмальгаузен. Квантовая электроника, 8, № 1, 57, 1981.

17. Г.Р.Локшин. Материалы xii Всесоюзной шкоды по голографии и когерентной оптике. Л., 93, 1980.