СИНТЕЗИРОВАНИЕ ГОЛОГРАММ ПРИ ВАРИАЦИИ ЧАСТОТЫ

В.Е.Куницын

Проводится теоретическое рассмотрение вопроса об уменьшении числа пространственных отсчетов волнового поля, необходимых для записи голограммы, путем регистрации поля на многих частотах. Уменьшение числа приемников важно для голографии на длинных акустических, сейсмических и радиоволнах.

Ввиду отсутствия непрерывных регистрирующих сред достаточно хорошего качества, регистрация голограмм полей акустических, сейсмических и радиоволн производится, как правило, точечными приемниками. Кроме того, необходимые размеры таких голограмм нередко столь велики, что применение непрерывных регистрирующих сред проблематично. Для восстановления с высокой разрешающей способностью полей названных типов волн требуется весьма большое число приемников, что трудно осуществись на практике. Отсюда сравнительно низкое качество восстановления в имеющихся экспериментах.

Между тем, известно, что в пределах полного числа информационных степеней свободы волнового поля можно взаимно менять соотношения между пространственными, временными и поляризационными степенями свободы, сохраняя при этом их полное число /1/. Как следствие названной теоремы, можно получать пространственное разрешение, используя временные степени свободы. Однако, как отмечается в /2/, пути реализации указанной принципиальной возможности не очевидны.

Здесь рассматривается метод регистрации голограмм и последующего восстановления волнового поля, использующий информацию о поле на различных частотах, что позволит существенно сократить число необходимых приемников /3/. Увеличение числа регистрируемых частот для полей акустических, сейсмических и

- 135 -

радиоволн, как правило, технически проще, чем увеличение числа приемников. Рассмотрение проводится без конкретизации вида волнового поля. Начало системы координат 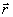= (,z) связано с объектом. На плоскости, ортогональной оси z, регистрируется голограмма i(,z) = | a + u| ² - интенсивность интерференционной картины между волной от объекта А, облучаемого волной 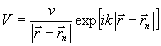передатчиком с координатами 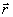_n, зависящая от длины волны l и вида опорной волны u, k = 2p l - волновое число. Частота опорной волны совпадает с частотой волны объекта.

Задача ставится следующим образом: используя информацию об i(,k), с разными k сформировать (синтезировать) обычную голограмму; назовем ее эквивалентной голограммой i₀(',k₀), которая получилась бы при регистрации интерференционной картины от волны объекта А₀ с постоянными k₀, u₀ и 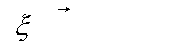, расположенным в точке 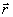'_n. При этой предполагается расширить область значений ', где определяется i₀ по сравнению с областью значений , на которых задана i. Если найти преобразование координат голограммы '(,k), переводящее i₀(',k₀) ® i(,k), то можно будет получать значения i₀ в разных точках ' эквивалентной голограммы, производя измерения в одной точке с разными значениями частота волн. В общем случае такое преобразование определяется объектом, но практическую ценность имеют преобразования при определенных условиях, не зависящие от вида объекта. Соотношение i₀(',k₀) = i(,k), можно рассматривать как уравнение относительно '(,k).

a₀(',k₀)u^*₀(',k₀) + a^*₀u₀ + | a_0| ² + | u_0| ² = a(,k)u^*(,k) + a^*u + | a| ² + | u| ² (1)

Искомое преобразование существует при опорной волне от точечного источника 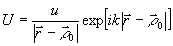, расположенного в ₀. В случае плоской опорной волны для того, чтобы существовало такое преобразование, необходимо производить дополнительную обработку принимаемого поля - домножение на фазовый множитель, зависящий от координат точек приема, что усложняет регистрацию. При условии А₀u^*₀ = au^* уравнение (1) удовлетворяется, правда, при этом может измениться уровень фона. Заметим, что в случае

- 136 -

голографии на акустических, сейсмических и радиоволнах опорные волны можно формировать искусственно, подавая опорные напряжения в каждый приемник, что позволяет имитировать любую опорную волну и отфильтровать фон. Перепишем условие А₀u^*₀ = Аu^*, используя выражение для воля объекта, излучающего или рассеивающего зондирующие волны в борновском приближении:

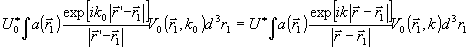(2)

Функция a(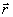) характеризует рассеивающие свойства объекта. Вообще говоря, а(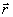) может зависеть и от частоты, но известным образом и одинаково для всех точек объекта. Важно, чтобы (2) выполнялось для любого объекта. После вычисления вариационной производная по а(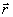₁) получается равенство, которое должно выполняться независимо от 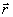₁. Для этого необходимы следуйте условие на расстройку волновых чисел и максимальные размеры объекта r _m, z_m по соответствующим осям:

z = z_m > r > r ₀ >>r _m, z_m; | k – k_0| z_m << 1; | (k – k₀)r ²_m/z| << 1 (3)

Разлагая по степеням r₁/r и r ₀/r, приравняем фазы упоминаемого выше равенства, при этом сомножители при 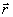₁ должны совпадать, поскольку фазовое равенство должно выполняться независимо от 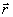₁. Отсюдаа следует искомое преобразование:

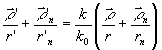(4)

Найденное преобразование позволяет, производя измерения интенсивности интерференционной картины одним приемником на многих частотах, синтезировать эквивалентную линейную апертуру. Тем самым существует возможность синтезировать эквивалентную голограмму. Важно, что указанные преобразования справедливы (при | k – k₀| << k₀) и в зоне Френеля, интересной для большинства практических приложений.

На основе (4) можно вывести аналитическую формулу для восстанавливаемого с голограммы поля 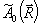. Измерение i проводится ℓ линейками приемников, расположение которых

- 137 -

задается функциями r _n(j ), где j полярный угол в плоскости приема.

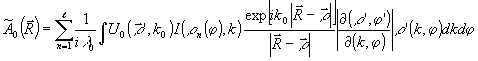(5)

Якобиан перехода к новым переменным k, j определяется (4). Соотношение (5) представляет собой обычный интеграл Кирхгофа по плоскости эквивалентной голограммы, в котором произведена замена переменных. Поскольку подынтегральное выражение состоит из А_0| u_0| ² + А^*₀u²₀, то восстанавливаемое с голограммы поле содержит как поле мнимого изображения a₀|u₀|², так и поле действительного изображения a^*₀u²₀.

Синтезируемая апертура Р пропорциональна расстройке волновых чисел и расстоянию между приемником и неподвижной точкой преобразования интерференционной картины Р = | r (k_max) - r (k_min)| » (k_max – k_min)| + r_n/r_n| . Неподвижная точка преобразования находятся в точке "зеркального отражения" .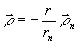

Выигрыш в числе приемников, равный числу используемых частот, ограничен условиями (3). В наиболее типичных случаях он равен 5 ¸ 20. Требуемый относительный сдвиг частоты обычно 10^-3 ¸ 10^-2. Если z_m << r _m, то можно синтезировать эквивалентную голограмму, используя одну линейку приемников.

Сложенный способ регистрации голограмм привлекает возможностью использования аналоговых схем обработки. Регистрируемая интенсивность интерференционной картины i(,k) на разных частотах пересчитывается (4) на эквивалентную голограмму i₀(',k₀). Целесообразно формировать эквивалентную оптическую голограмму и проводить восстановление поля в реальном масштабе времени. Возможна и цифровая обработка регистрируемых сигналов на основе (5).

Литература

1. Л.М.Сороко. Основы голографии и когерентной оптики, М., "Наука", 1971.

2. Голография. Метода и аппаратура, под ред. В.М.Гинзбург и Б.М.Степанова, М., "Сов. радио", 1974.

3. В.Д.Гусев, В.Е.Куницын. Доклад АН cccp, № 4, 252, 1980.