Media-security

ОБ ОДНОМ ВАРИАНТЕ УМЕНЬШЕНИЯ ЧУВСТВИТЕЛЬНОСТИ ГОЛОГРАФИЧЕСКОЙ ИНТЕРФЕРОМЕТРИИ ПРИ ИЗМЕРЕНИИ ПРОГИБОВ

С.Б.Артеменко

Рассмотрены вопросы чувствительности голографической интерферометрии к измерению прогибов пластин. Показана возможность ее значительного понижения для определенного класса объектов. Приведены некоторые экспериментальные результаты.

Метод голографической интерферометрии находит широкое применение в экспериментальной механике для определения компонент вектора смещения. Наиболее просто этим методом изучаются перемещения из плоскости деформируемой детали. Обладая рядом бесспорных достоинств: бесконтактностью, апостериорностью, констинуальностью, отсутствием особых требований к чистоте обработки изучаемых поверхностей, возможностью контроля за соблюдением граничных условий в ходе эксперимента и т.п., - голографическая интерферометрия диффузно-отражающих объектов в ее общепринятом варианте оказывается зачастую чрезвычайно чувствительным методом с низкой помехоустойчивостью. К тому же из-за ограниченного разрешения оптических систем невозможен надежный замер прогибов в местах с их резким градиентом. Перечисленные обстоятельства заставляют искать пути снижения чувствительности метода.

Для расширения диапазона измеряемых перемещений в ряде работ рассматриваются методы типа разностных контурных карт, а также основанные на объединении методов Муара и голографии. Однако трудоемкость и низкий контраст получаемых картин препятствует их широкому распространению.

Будем понимать под чувствительностью, как это принято в измерительной технике /1/, отношение изменения показания прибора

- 99 -

к величине возмущения., вызвавшего это отклонение. В нашем случае отношение выходной величины к входной будет равно числу полос, приходящихся на единицу смещения. Тогда, следуя гипотезе идентичных точек /2/, определим чувствительность голографической интерферометрии следующим образом:

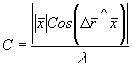(1)

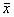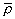где = ₀ + 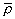_Н - вектор суммы единичных векторов освещения 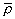₀ и наблюдения 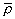_Н; D 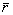- вектор смещения; l - длина волны.

Из формулы (1) видно, что для изменения чувствительности можно варьировать все три параметра, стоящие в правой части. Однако пределы варьирования l ограничиваются техническими возможностями аппаратуры, а значительное уменьшение как 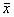, так и Сos(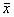^D 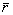) приводит к неудобному скользящему наблюдению /3/ и, в свою очередь, вызывает рост ошибки в определении местоположения полосы. Уменьшение угла наблюдения с исследуемой поверхностью до 10° привело к снижению чувствительности до величины С = 0,5·10⁶ м, которая, тем не менее, на порядок превосходит чувствительность теневого муарового метода с использованием высокочастотных растров.

Между тем, для диффузно-пропускающих объектов можно указать более естественный путь понижения чувствительности за счет снижения 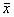, но без ухудшения условий наблюдения. Перепишем формулу (1) в координатной форме, учитывая правило А.Эйнштейна о суммировании по повторяющемуся индексу:

c = | cos_{iD r}(cos_i0 + cos_ih)| /l (2)

где cos_{iD r;0;h} - суть направляющие косинусы единичных векторов смещений, освещения и наблюдения в 3-х мерном ортонормированном базисе 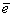_i. Начало этой произвольно ориентированной системы координат x_i находится в точке, о смещении которой имеется какая-либо априорная информация; i = 1,2,3 - индекс, указывающий ось координат.

Формулу (2) можно упростить до одного слагаемого, если известно направление вектора смещения. Тогда, направив вдоль

- 100 -

него какую-либо ось Х_j, получим следующую формулу:

c = | cos a_j0 + cos a_jh|/l (3)

На рис.1 приведена шкала чувствительности различных методов определения прогибов по сравнении с предложенным. Следует учесть, что резко обозначенные границы на самом деле несколько размыты в зависимости от конкретного способа реализации того или иного метода.

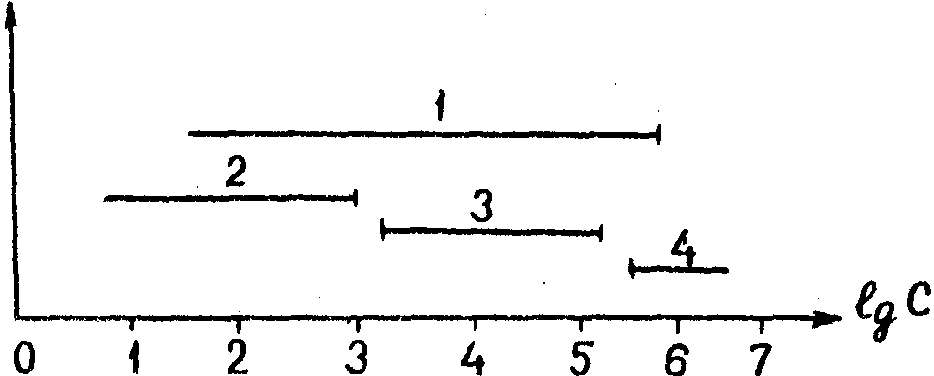
Рис.1. Шкала чувствительности бесконтактных методов определения прогибов:

1 - предлагаемый способ; 2 - геодезические и фотограмметрические методы; 3 - методы муаровых полос и спекл-интерферометрии; 4 - голографометрия в диффузно-отраженном излучении.

Из (3) следует c_max = 2/l . Удобнее, однако, пользоваться безразмерной величиной чувствительности s:

s = c/c_max = | cos a_j0 + cos a_jh|/l (4)

На рис.2 приведена номограмма изолиний чувствительности в зависимости от геометрии схемы. По ней нетрудно определить, что значительного снижения чувствительности можно добиться при изучении прогибов диффузно-пропускающих объектов. На рис.3 приведена векторная схема, поясняющая принцип понижения чувствительности

- 101 -

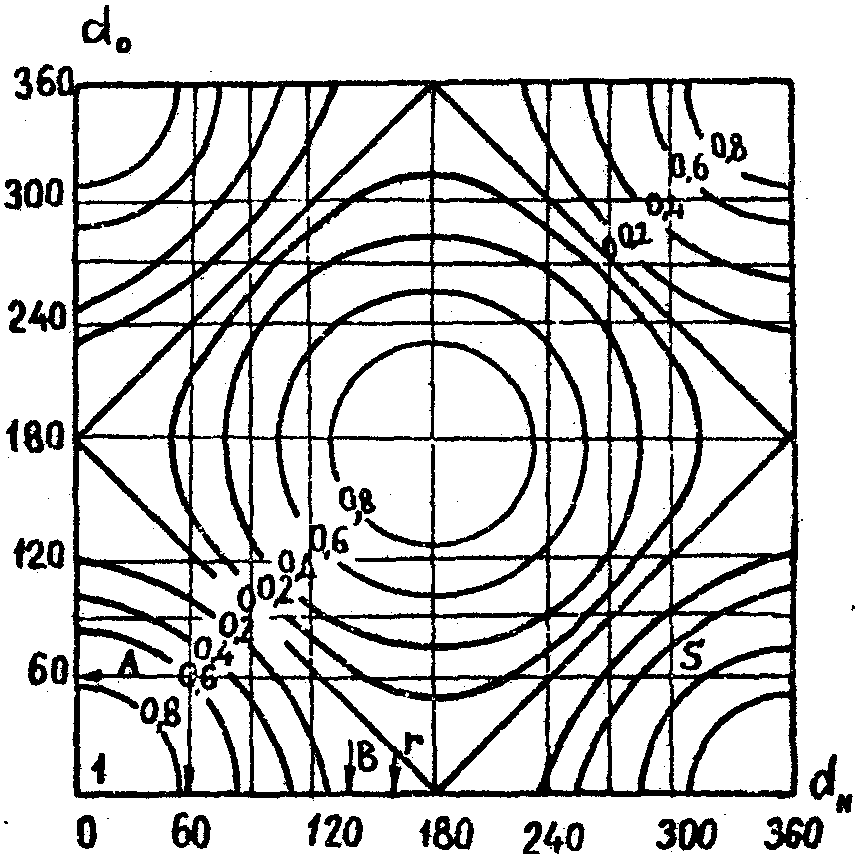
Рис.2. Номограмма чувствительности голографической интерферометрии.

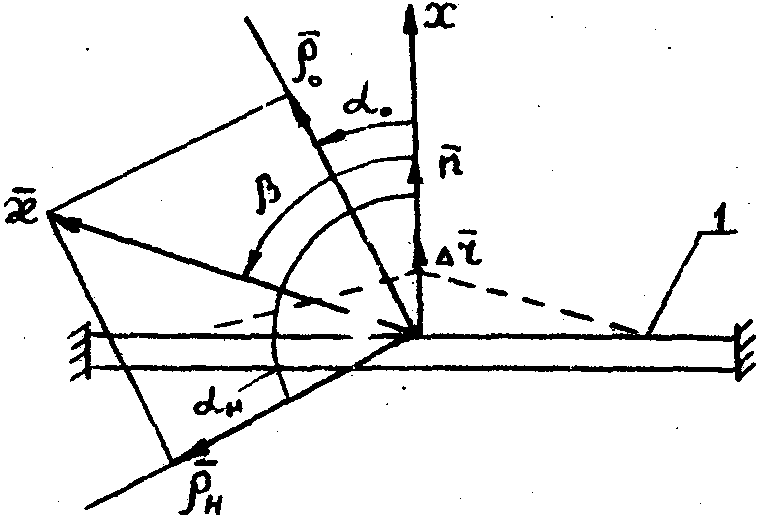
Рис.3. Векторная схема проведения эксперимента.

- 102 -

за счет наблюдения объекта со стороны, противоположной освещению. На рис.4 показана одна из возможных схем проведения эксперимента. По этой схеме были испытаны защемленные по контуру квадратная и треугольная пластины. При одном и том же прогибе изменение угла наблюдения в пределах апертуры голограммы приводило к снижению числа полос на восстановленном изображении с 11 до 2. Оценка экспериментально измеренных прогибов с теоретическим решением /4/ выявила их расхождение в пределах (4 ¸ 10)%.

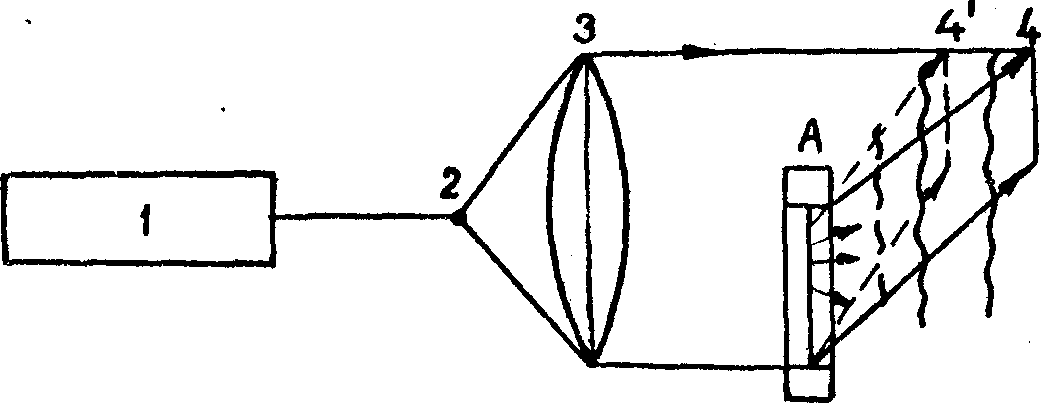
Рис.4. Схема топографического интерферометра с пониженной чувствительностью к определению прогибов.

Мотаю также показать, что дополнительный набег фазы, связанный с углами поворота при изгибе диффузно-пропускающих пластин довольно мал. Так, при нормальном падении объектной волны, толщине пластины 2 мм, показателе преломления n = 1,5 и угле поворота j = 10^-2 фаза меняется всего лишь на » p /10.

Рассмотренный способ измерения прогибов можно рекомендовать для изучения потери устойчивости пластин при их продольном сжатии.

В заключение автор выражает глубокую признательность профессору Островскому Ю.И. за поддержку в работе.

- 103 -

Литература

1. С.Г.Рабинович. Погрешности измерений. Л., Энергия, 1978.

2. Е.Б.Александров, М.А.Бонч-Бруевич. ЖТФ, 37, 360, 1967.

3. Н.Г.Вдасов и др. Тезисы докладов iii-го Всесоюзного семинара "Оптико-геометрические методы исследования деформ. и напр.", Днепропетровск, стр.54-55, 1978.

4. С.Б.Артеменко. Тезисы Уральской зональной конференции по механике сплошных сред. Часть i, Пермь, crp.10-11, i980.