АНАЛИЗ МЕТОДОВ ИССЛЕДОВАНИЯ ФАЗОВОГО РАСПРЕДЕЛЕНИЯ ИНТЕРФЕРЕНЦИОННОГО ПОЛЯ

С.В.Гордеев, В.П.Горелик, Б.Г.Турухано, Н. Турухано

Прямое решение задачи исследования фазового распределения интерференционного поля традиционными методами классической и голографической интерферометрии требует использования высокоточного эталонного элемента. Рассматриваются методы относительных измерений фазовых характеристик интерференционного поля, позволяющие исключить необходимость применения эталонного элемента.

Интерференционные методы исследования физических процессов и широкого круга объектов основываются прежде всего на исследовании фазовых характеристик интерференционного поля. Помимо исследовательских целей, изучение этих характеристик позволяет синтезировать новый класс оптических элементов - голографические дифракционные элементы, которые в настоящее время являются одними из наиболее важных инструментов, используемых в интерференционных методах исследования. К числу голографических дифракционных элементов относятся голографические дифракционные решетки, применяемые в спектроскопии и метрологии, голографические решетки с изменяющимся периодом, используемые для осуществления преобразований Гильберта и Меллина, голографические линзы, мультипликаторы изображения и т.д.

Дальнейшее совершенствование и создание новых голографических дифракционных элементов непосредственно связано с развитием методов исследования фазовых характеристик интерференционных полей.

- 25 -

1. Метода классической интерферометрии

Основной задачей классической интерферометрии является изучение формы волнового фронта, характеризующего исследуемый объект. В классических интерферометрах сравнения типа Тваймана-Грина, Маха-Цандера, Физо /1-3/ изучение формы волнового фронта осуществляется посредством сравнения исследуемого волнового фронта с опорным, формируемым эталонным элементом сравнения. В качестве эталонного элемента обычно используется высококачественная плоская или сферическая поверхность. Для исследования поверхностей сложной формы (например, асферических поверхностей) вводится дополнительная голограмма-компенсатор /4/.

В отличие от интерферометров сравнения в классических интерферометрах сдвига отсутствует вспомогательный эталонный элемент. Исследование формы волнового фронта основывается на анализе интерференционной картины взаимодействия двух одинаковых, сдвинутых в пространстве друг относительно друга волновых фронтов /5,6/ к настоящему времени существуют многочисленные схемные варианты, позволяющие осуществить сдвиг в пространстве -интерферометр Мерти (плоскопараллельная пластина) /7,8/, система из двух дифракционных решеток - (Ронки-тест) /9,10/, призма-куб /11/ и т.д.

Несмотря на указанные различия в принципе работы классических интерферометров сдвига и сравнения, общим обстоятельством определяющим в конечном счете точность исследования формы волнового фронта, является качество изготовления элементов сдвига и сравнения. Это обстоятельство становится тем более существенным при исследовании протяженных волновых фронтов, поскольку в этом случае точность изготовления элементов сдвига и сравнения обычно не превосходит l /10.

Возвращаясь к вопросу исследования фазовых характеристик интерференционного поля, следует выделить два основных момента:

1. традиционные классические методы не предполагают исследование фазовых характеристик интерференционного поля, формируемого двумя или более волновыми фронтами;

2. несмотря на декларируемую в ряде работ точность порядка

- 26 -

l /100 /3,11/ следует подчеркнуть, что в данном случае такая точность является относительной и обусловлена качеством элементов сдвига и сравнения.

Однако в работе /12/ показана возможность исследования фазовых характеристик протяженного интерференционного поля с помощью достаточно простого интерферометра сдвига в виде плоскопараллельной пластины. При этом точность измерений мало зависит от качества самого интерферометра.

Суть метода заключается в том, что одним и тем же интерферометром сдвига раздельно исследуются, а затем сравниваются волновые фронты интерферирующих волн. Для этого интерферометр сдвига последовательно и адекватно располагают относительно каждого волнового фронта. В этом случае аберрации самого интерферометра являются постоянной величиной, аддитивно входящей в результаты каждого измерения, и с большой точностью могут быть исключены на этапе сравнения.

Рассмотрим однокоординатное представление, которое можно легко обобщить на случай двух координат. Пусть интерференционное поле образуется двумя квазиплоскими волнами, пересекающимися под углом q (рис.1).

Комплексные амплитуды этих волн в плоскости

s1(x) = exp{i[k1x + ¦ 1(x)]}	(1)
s2(x) = exp{i[k2x + ¦ 2(x)]}

где k₁ и К₂ - волновые числа; ¦ ₁(х) и ¦ ₂(x) - функции, определяющие отклонение фазового распределения квазиплоской волны от фазового распределения ближайшей опорной плоской волны.

Фазовое распределение интерференционного поля вдоль оси ОХ можно записать в виде

Ф(х) = 2Кх + D ¦ (x) (2)

где К = К₂ – К₁; D ¦ (x) = ¦ ₂(x) - ¦ ₁(x).

Второй член выражения (2) описывает отклонение исследуемого интерференционного поля от идеального. Поместим интерферометр

- 27 -

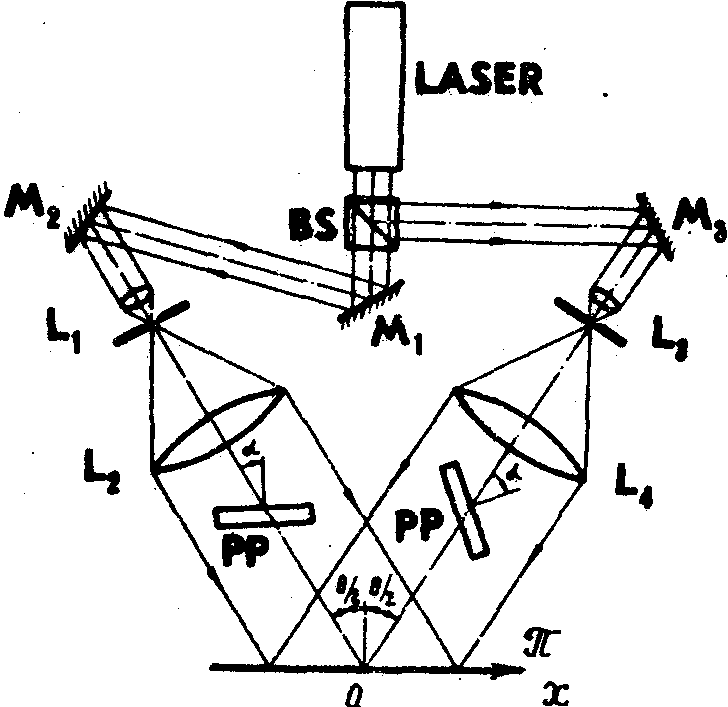
Рис.1. Схема формирования исследуемого интерференционного. поля:

РР- интерферометр сдвига; bs- делитель пучка; М₁,М₂, М₃ - зеркала; l₁,l₂,l₃,l₄ телескопические системы; p - плоскость исследования фазового распределения интерференционного поля.

сдвига в поле волны s₁(x) симметрично относительно оси пучка (рис.1). Тогда для разности фаз D j ₁(x) между точками х и x₀ в выходной плоскости интерферометра сдвига можно записать:

D j ₁(x) = [¦ ₁(x + x ) - ¦ ₁(x) + W (x)] – [¦ ₁(x₀ + x ) - ¦ ₁(x₀) + W (x₀)] (3)

где x - величина сдвига вдоль оси Оx, W (x) - член, определяющий аберрации интерферометра сдвига.

Помещая интерферометр сдвига в поле волны s₂(x) адекватно относительно оси второго пучка, имеем:

D j ₂(x) = [¦ ₂(x + x ) - ¦ ₂(x) + W (x)] – [¦ ₂(x₀ + x ) - ¦ ₂(x₀) + W (x₀)] (4)

- 28 -

Вычтем (3) из (4), тогда

D j ₂(x) - D j ₁(x) = [D ¦ (x + x ) - D ¦ (x)] – [D ¦ (x₀ + x ) - D ¦ (x₀)] (5)

Из уравнения (5) можно записать рекуррентное соотношение для значений D ¦ (x) в ряде эквидистантных точек, расположенных с периодом вдоль направления сдвига

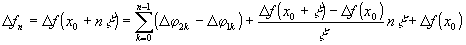(6)

где D j _1k и D j _2k - измеряемые в эксперименте разности фаз между 0-ой и k-ой точками.

Данным методом можно определить фазовое распределение интерференционного поля с точностью до произвольных второго и третьего слагаемых в уравнении (6). Однако, эти слагаемые можно задать граничными условиями. Для этого выберем волновое число 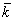опорного интерференционного поля таким, чтобы

D ¦ (x₀) = D ¦ (x₀ + x n) = 0 (7)

где n = 1, 2...n - 1; n = [d/x ] - полное число точек; d - апертура поля.

Тогда

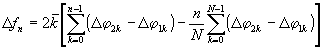(8)

Уравнение (6) описывает нормированное к опорному полю фазовое распределение исследуемого интерференционного поля.

Точность метода в значительной степени определяется адекватным размещением интерферометра сдвига относительно осей пучков. Нетрудно убедиться, что погрешность D х в установке центра интерферометра сдвига относительно оси пучка приведет к появлению фазовой ошибки

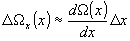
а погрешность в установке угла наклона D a -

- 29 -

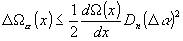(10)

где d_n - размер плоскопараллельной пластины. Так, если качество интерферометра сдвига таково, что

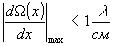
то при D х < 0,1 мм и D a < 0, 5°

| D W (х)| _max < l /100

Резюмируя, следует отметить, что рассмотренный метод предъявляет легко выполнимые требования как к установке интерферометра сдвига, так и к самой процедуре фазовых измерений и позволяет исследовать фазовое распределение интерференционного поля с высокой точностью, превосходящей точность изготовления самого интерферометра.

ii. Методы голографической интерферометрии

Область применения методов классической интерферометрии ограничена в силу следующих обстоятельств:

1. Методами классической интерферометрии можно исследовать в основном зеркально-отражающие или прозрачные объекты сравнительно простой формы.

2. Методы классической интерферометрии не предполагают апостериорное исследование различных состояний объекта.

3. Точность интерферометрических измерений в значительной степени обуславливается качеством классического интерферометра.

Указанные недостатки не присущи методам голографической интерферометрии /13-17/. в основе голографической интерферометрии лежит запись голограммы объекта, которая представляет собой "замороженное" исходное интерференционное поле с последующим сравнением интерференционного поля, соответствующего изменившемуся состоянию объекта с исходным. При этом сравнение может производиться как с реальным интерференционным полем (метод реального времени), так и с записанным на фотоноситель (метод двух экспозиций и метод записи на раздельные голограммы). На этапе сравнения аберрации голографического интерферометра практически

- 30 -

полностью исключаются /18/.

И отличие от классической интерферометрии, исследующей форму единичного волнового фронта голографическая интерферометрия позволяет исследовать фазовое распределение двух или более интерференционных полей.

Следует отметить то существенное обстоятельство, что для традиционных методов голографической интерферометрии /19/ принципиально важной является разность фазовых распределений интерференционных полей. Задача исследования фазового распределения единичного интерференционного поля в духе основных концепций указанных методов может быть решена лишь путем создания идеального интерференционного поля сравнения, что является достаточно сложной задачей, лишающей к тому же традиционные методы одного из главных преимуществ - возможности использования голографического интерферометра невысокого качества.

Для решения указанной задачи в работе /20/ предложено использовать подвижную, согласованную по периоду с исследуемым интерференционным полем голографическую решетку. Впервые взаимодействие интерференционного поля с подвижной согласованной дифракционной решеткой было рассмотрено в работах /21,22/ доказано, что образующаяся при этом картина муаровых интерференционных полос обусловлена фазовым распределением интерференционного поля и аберрациями дифракционной решетки. Влияние решетки можно исключить, перемещая ее относительно исследуемого поля и снимая информацию о фазовом распределении в системе точек. жестко связанных с перемещающейся решеткой. Тогда изменение разности фаз между точками будет однозначно определяться только фазовым распределением интерференционного поля. Дополнительная разность фаз, вносимая самой решеткой, будет постоянной величиной, аддитивно входящей в каждый акт измерения. Роль идеального интерференционного поля сравнения в данном методе играет абстрактное интерференционное поле, определяемое граничными условиями, соответствующими физическому смыслу решаемой задачи.

Пусть интерференционное поле в плоскости p формируется двумя квазиплоскими волнами единичной амплитуда (рис.1):

- 31 -

s₁(x,y) = exp{i[k_1xx + k_1yy + y ₁(x,y)]} (11)

s₂(x,y) = exp{i[k_2xx + k_2yy + y ₂(x,y)]} (12)

где К_1x, k_2x, k_1y, К_2y - проекции волновых векторов y ₁(x,у) и y ₂(x,y) - функции, описывающие отклонение волнового фронта от ближайшего плоского опорного волнового фронта. Запишем в плоскости p голографическую дифракционную решетку с амплитудным пропусканием

t µ cos[2k_gx + y ^g(x,y)] (13)

где К_g = k_2x – k_1x волновое число решетки, функция y ^g(x,y) описывает отклонение фазового распределения реальной голографической решетки от фазового распределения ближайшей опорной идеальной решетки. При взаимодействии интерференционного поля с голографической решеткой в плоскости p образуется картина интерференционных муаровых полос с фазовым распределением

Ф(х,у) = Ф^ид(x,y) + y ^g(x,y) - y (x,y) (14)

где y (x,y) = y ₂(x,y) - y ₁(x,у) - функция, описывающая фазовое распределение исследуемого интерференционного поля, a Ф^ид(x,y) описывает фазовое распределение в интерференционной картине взаимодействия двух идеальных плоских волн и идеальной плоской голографической решетки.

Задача состоит в том, чтобы определить значения функции y (х,y) в плоскости p .

Вначале определим y (х,у₀) вдоль сечения у = у₀ (рис.2). Следуя уравнению (14), разность фаз между точками (х₀,у₀) и (х₀ + x ,y₀) можно записать в виде:

D Ф(x ) = D Ф^ид + [y ^g(x₀,y₀) - y ^g(x₀ + x ,y₀)] – [y (x₀,y₀) - y (x₀ + x ,y₀)] (15)

Если согласованная голографическая дифракционная решетка перемещается строго вдоль оси ОХ каждый раз на одно и то же

- 32 -

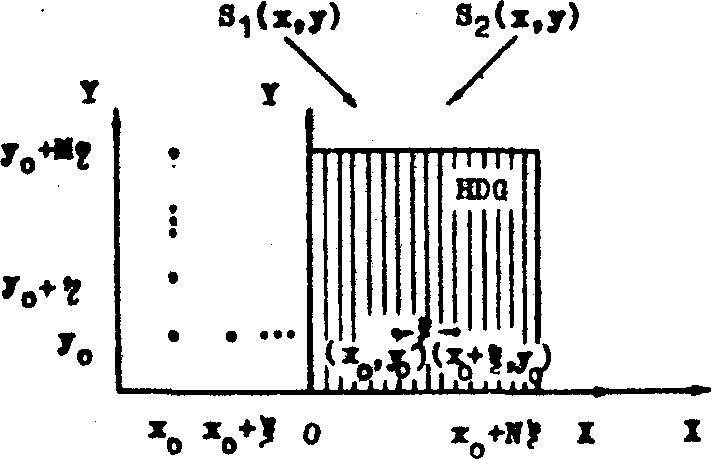
Рис.2. Схема исследования фазового распределения интерференционного поля в сечениях: s₁(x,y); s₂(x,y) - квазиплоские волновые фронты, формирующие интерференционное поле.

расстояние и разность фаз измеряется в одних и тех же точках, жестко связанных с дифракционной решеткой, то второй член уравнения (15) будет оставаться неизменным. Поэтому, т.к. D Ф^ид = const, изменения D Ф(x ) будут вызываться лишь неравномерностью распределения интерференционных полос поля, в котором перемещается решетка. Из уравнения (15) можно записать рекуррентное соотношение для значений y (x,y₀) в ряде равноотстоящих точек

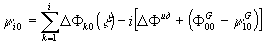(16)

где

y _ij = y (x₀ + ix ,y₀ + jh ); y ^g_ij = y ^g(x₀ + ix ,y₀ + ih )

a

D Ф_k0(x ) = D Ф^ид + [y ^g₀₀ - y ^g₁₀] – [y _k-1,0 - y _k0] (17)

- измеряемые в эксперименте разности фаз.

Уравнение (16) позволяет определить значение y _i0 с точностью до линейного слагаемого вида

- 33 -

D Ф₀₀(x ) – i[D Ф^ид + (y ^g₀₀ - y ^g₁₀)] (18)

которое можно определить из граничных условий

y ₀₀ = 0 (19)

y _n0 = 0 (20)

где n - полное число отсчетов разности фаз вдоль оси ox. Тогда уравнение (16) с учетом граничных условий (19) и (20) перепишется в виде

; i = 1,2,…n (21)

Подобным же образом можно определить значения y _ij в сечениях, параллельных оси ОХ: у₀ + h ; y₀ + 2h ... y₀ + mh (рис.2), где М - полное число отсчетов вдоль оси oy.

Однако, выбор граничных условий по аналогии с (19) и (20) неправомерен, т.к. в данном случае они должны определяться из конфигурации начальной y _0j и конечной y _nj полос интерференционного поля.

Перейдем к анализу конфигурации начальной полосы интерференционного поля. Для этого воспользуемся зеркальным отображением штриха согласованной голографической дифракционной решетки. Повернем решетку на 180° вокруг штриха идеальной решетки, тогда

y ^g_0j - y ^gид_0j = -y ^rg_0j - y ^gид_0j (22)

где символ r - означает вращение.

Принимая во внимание, что D Ф^ид = D Ф^rид и ставя граничные условия

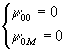(23)

можно определить конфигурации начальной полосы поля уравнением

- 34 -

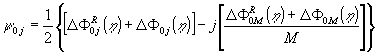(24)

где

D Ф_0j(h ) = D Ф^ид_0j + (y ^g₀₀ - y ^g_oj) – (y ₀₀ - y _0j) (25)

и

D Ф^r_0j(h ) = D Ф^ид_0j + (y ^rg₀₀ - y ^rg_oj) – (y ₀₀ - y _0j) (26)

- измеряемые в эксперименте разности фаз при определении формы начальной полосы.

Для вычисления y _ij мы поставили три произвольных граничных условия (19), (20) и (23) и таким образом задали плоскость сравнения в фазовом пространстве. В общем случае для четвертого граничного условия

y _nm = a ¹ 0 (27)

Это означает, что значение y _nm может находиться вне плоскости сравнения, определяемой первыми трем граничными условиями. Для определения y _nm рассмотрим разность фаз между точками: 1 - (x₀,y₀ + mh ); 2 - (х₀,у₀); 3 - (x₀+nx ,y₀+mh ); 4- (x₀ + nx ,y₀) (рис.2).

Нетрудно убедиться, что с учетом граничных условий (19) (20), (23)

a = [y (4) - y (1)] – [y (2) - y (3)] (28)

Повернем голографическую решетку в плоскости p на 180° вокруг точки, являющейся центром симметрии прямоугольника 1-2-3-4. Обозначая символом (~) поворот решетки и учитывая, что после поворота 1 Þ 4; 2 Þ 3; 3 Þ 2; 4 Þ 1, можно записать

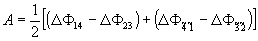(29)

где D Ф - значения разности фаз в соответствующих точках.

- 35 -

Аналогично (24), можно записать уравнение конечной полосы интерференционного поля в виде

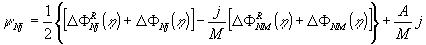(30)

Значения y _0j и y _nj представляют собой граничные условия для фазового распределения интерференционного поля вдоль сечений y₀ + jh = const.

Уравнение для y _ij определяется путем решения уравнения (16) с граничными условиями (24), (30) в виде

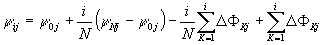(31)

где D Ф_kj — значения разности фаз вдоль сечений y₀ + ih = const.

Уравнения (24), (30), (31) описывают фазовое распределение интерференционного поля относительно заданной граничными условиями (19), (20) и (23) опорной плоскости в фазовом пространстве.

Экспериментальная проверка точности метода заключалась в следующем. Проводились две серии измерений. Вначале измерялось фазовое распределение y ⁱ_ij оптимальной настройке телескопических систем (рис.3). Затем одна из систем расфокусировалась, что приводило к появлению сферической составляющей. Фазовое распределение интерференционного поля со сферической составляющей y ⁱⁱ_ij приводится на рис.4.

Из разности y ⁱⁱ_ij - y ⁱ_ij вычиталось фазовое распределение ближайшего сферического волнового фронта сравнения. Результирующее фазовое распределение, представленное на рис.5, иллюстрирует экспериментальную точность измерений, которая по всему полю не превышает l /100.

Описанный метод позволяет измерять фазовое распределение интерференционного поля без применения эталона. Трудоемкий процесс определения y _ij выполняется только один раз, т.к. по известным значениям y _ij можно найти фазовое распределение штрихов самой голографической решетки y ^g_ij. Затем методом сплайн-интерполяции можно по значениям y ^g_ij, заданным на

- 36 -

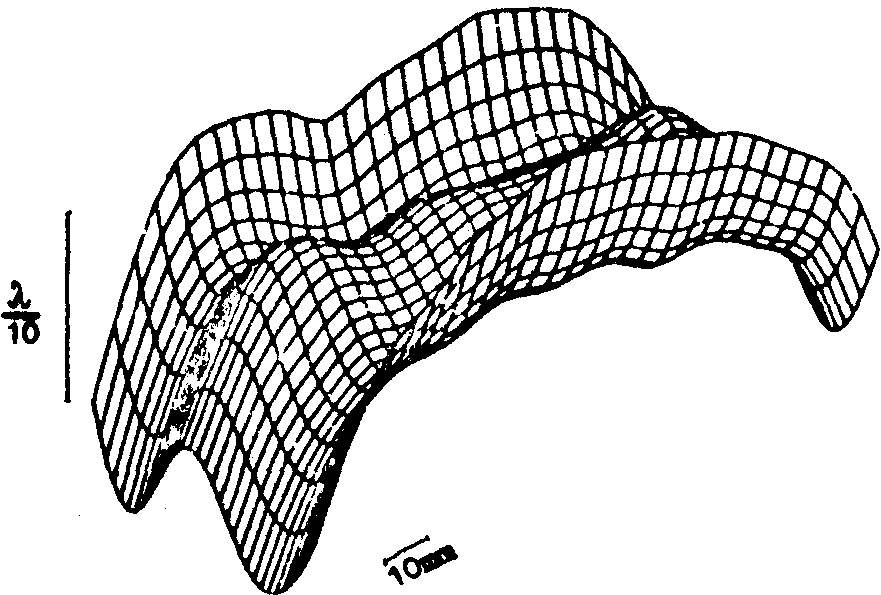
Рис.3. Фазовое распределение интерференционного поля y ⁱ_ij.

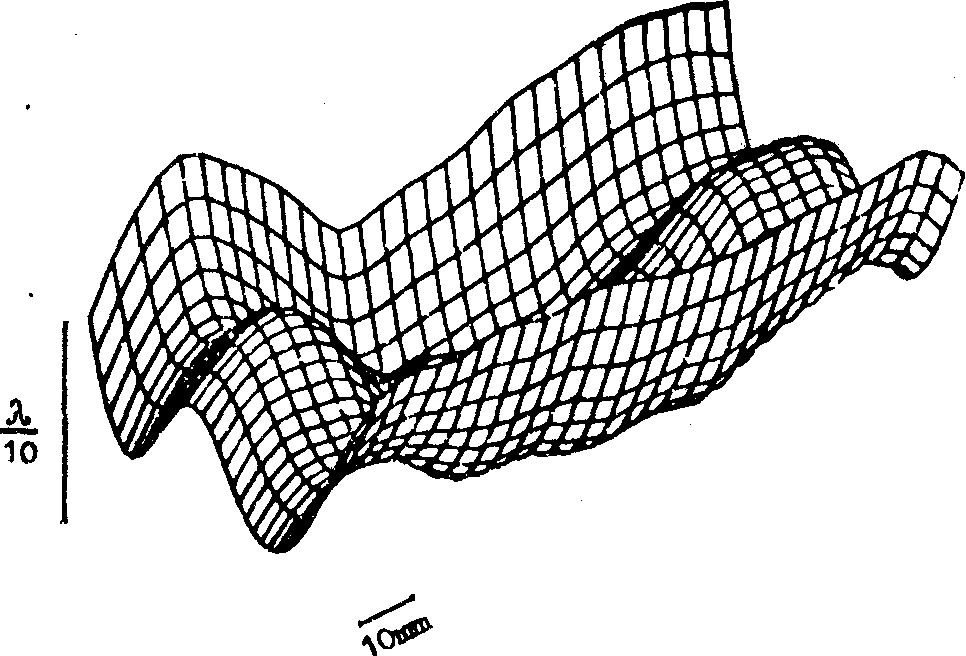
Рис.4. Фазовое распределение интерференционного поля со сферической составляющей y ⁱⁱ_ij.

- 37 -

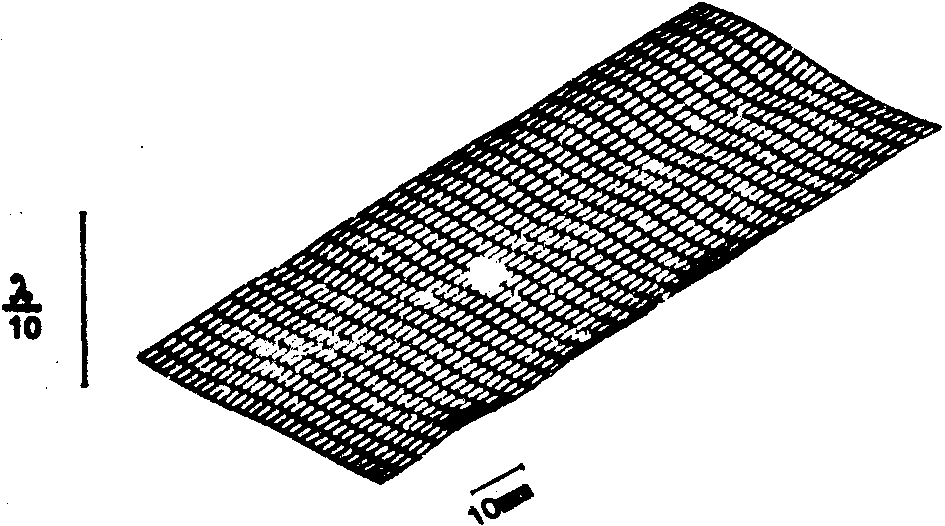
Рис.5. Результат сравнения разности y ⁱⁱ_ij - y ⁱ_ij с ближайшей сферой. (Экспериментальное подтверждение точности метода).

массиве n ´ М точек определить как y ^ig(х,у), так и y (x,y) в любой точке апертуры интерференционного поля. Имея измеренную таким способом голографическую решетку, можно производить фазовые измерения интерференционного поля обычным сканированием. Это позволяет исследовать поля, имеющие значительные аберрации.

iii. Заключение

Анализ методов исследования фазового распределения интерференционного поля показал, что прямое решение задачи исследования фазового распределения единичного интерференционного поля традиционными методами классической и голографической интерферометрии требует использования высокоточного эталонного элемента, создание которого является достаточно сложной самостоятельной проблемой.

Однако, поскольку в целом ряде физических задач необходимо определить отклонение фазового распределения исследуемого интерференционного поля от ближайшего идеально равномерного распределения, то прямые измерения могут быть заменены относительными.

- 38 -

При этом роль идеального интерференционного поля сравнения может играть абстрактнее интерференционное поле, определяемое граничными условиями, отвечающими физическому смыслу решаемой задачи.

В этом случае задача исследования фазового распределения интерференционного поля может быть решена с помощью подробно рассмотренных методов, использующих классический интерферометр Мерти /12/ и подвижную голографическую дифракционную решетку /20/.

Литература '

1. h.d.polster, j, pastor, k.m.scott, r.crane, p.h.langeubeck, pilston r., g.stainberg. new development in interferometry, appl.opt., v8, 521, 1969.

2. d.g.kocher. twyman-green interferometer to test large aperture optical systems. appl.opt., 11, 1872, 1972.

3. j.h.bruning, d.r.herriot, j.e.callengher, d.p.rosenfeld. digital wavefront measuring interferometer for testing optical surfaces and lense. appl.opt., 13, 2693, 1974.

4. m.fauld, a.p.fercher, r.torge and r.n.wilson. optical testing by means of synthetic holograms and partial lens compensation. opt.commune., 7, 363, 1973.

5. j.b.saunders. measurement of wavefronte without a reference standard. j.bes.nat.bor.stand. 65b, 239, 1961.

6. o.bryngdahl. application of shearing interferоmеtry. in progress in optics, 4, 39, 1965.

7. m.v.r.k.murty, the use of a single plane paralel plate as a lateral shearing interferometer with a visible gas laser source. appl.opt., 3, 531, 1964.

- 39 -

8. de vany a.s. scaning murty interferometer for optical testing. appl.opt., 11, 1467, 1972.

9. v.ronchl. forty years of history of grating interferometer. appl.opt., 3, 437, 1964.

10. y.ronchi. on the phase grating interferometer. appl.opt., 4, 1041, 1965.

11. d.nyyssonen and j.m.jerke. lens testing with a simple wavefront shearing interferometer. appl.opt., 12, 2061, 1973.

12. С.В.Гордеев, В.П.Горелик, Б.Г.Турухано, Н.Турухано. Исследование интерференционного поля интерферометром сдвига методом сравнения. Препринт ЛИЯФ. -684, Л., 1981.

13. Ю.И.Островский, М.М.Бутусов, Г.В.Острсвская. Голографическая интерферометрия. М., "Наука", 370, 1977.

14. r.e brooks, l.o.heflinger and r.f.wuerker. interferonetry with a holographically reconstructed comparison beam. appl.phys.lett., 7, 248, 1965.

15. g.l.rogers. "the equivalent interferometer" in holography. opt.acta, 17, 527, 1970.

16. l.o.heflinger, r.f.wuerker and r.e.broocs. holographic interferometry. j.appl.phys., 37, 642, 1966.

17. r.dandliker. heterodyne holographic iriterferometry in progress in optica, 17, 13, 1980.

18. А.К.Бекетова, Л.Т.Мустафина, А.Я.Смоляк. О допустимой деформации волновых фронтов в голографическом интерферометре. Опт. и спектр., 39, 336, 1975.

19. А.К.Бекетова, А.Ф.Белозеров, А.Н.Березкин и др. Голографическая интерферометрия фазовых объектов. Л., "Наука", 232, 1979.

- 40 -

20. С.В.Гордеев, В.П.Горелик, Б.Г.Турухано, Н.Турухано. Подвижная топографическая решетка как измерительные элемент при исследовании интерференционного поля. Препринт ЛИЯФ.-683, Л., 1981.

21. В.В.Добырн, Б.Г.ЧУрухано, Н.Турухано. Метрологические свойства комбинации интерференционного поля и голографической дифракционной решетки. Опт. и спектр., 30, 550, 1971

22. Б.Г.Турухано, Н.Турухано. Голографические системы для измерения линейных перемещений и фазовых сдвигов. Материалы, iii Всесоюзной школы по голографии. Л., 213, 1972.