ВОЛНЫ ПОЛЯРИЗАЦИИ В СИСТЕМАХ С ФАЗОВОЙ ПАМЯТЬЮ

Е.И.Штырков

Рассмотрены свойства монохроматических волн поляризации (когерентные материальные волны в веществе), генерируемых в динамической регистрирующей среде с фазовой памятью при помощи разнесенных во времени оптических монохроматических полей.

В настоящее время все больший интерес вызывает неодновременное параметрическое взаимодействие электромагнитных оптических волн с веществом. Под этим взаимодействием понимают процессы, происходящие в веществе при облучении его короткими импульсами когерентного света, разнесенными во времени на интервал, больший чем их длительность. Взаимодействие этих волн становится возможным лишь через среду и, естественно, только в том случае, когда вещество обладает достаточно длинной фазовой памятью. В такой ситуации каждый импульс поля накачки передает информацию о своих волновых характеристиках в среду, и эта информация сохраняется здесь до прихода следующих импульсов накачки. Поэтому, когда мы говорим о неодновременном взаимодействии, то это не означает нарушение причинных связей, несмотря на то, что сами оптические волны накачки не встречаются друг с другом и поэтому не могут интерферировать непосредственно. В данном случае регистрирующая среда является своеобразным волновым мостом, связывающим волновые характеристики отдельных оптических полей. О том, каким образом среда с фазовой памятью отображает волновые свойства накачки, обладая при этом способностью записывать, восстанавливать и преобразовывать волновые фронты света, о формировании светоиндуцированных решеток при помощи разнесенных во времени неколлинеарных импульсных пучков света, достаточно

- 7 -

написано ранее (см., например /1/). Однако, хотелось бы более наглядно показать, каким образом осуществляется связь волновых характеристик полей накачки. Поэтому, в дайной работе предполагается рассмотреть эволюцию поведения неравновесной микроскопической поляризации, наводимой в среде, ее влияние на формирование когерентной инверсии и материальных волн возмущений, которые, как известно, являются основными характеристиками когерентных суперпозиционных состояний атомного ансамбля. Рассмотрим накачку системы атомов в условиях одноквантового резонанса при помощи последовательности коротких и мощных импульсов света в виде неколлинеарных плоских пучков с волновыми векторами ₁, ₂, ₃ .… Если в системе атомов подавлены каналы необратимой релаксации, то наведенная неравновесная поляризация имеет вид монохроматических волн, обусловленных согласованным колебанием диполей, локальное положение которых для твердого тела можно считать фиксированным. В промежутке между импульсами эти волны поляризации (волны материальных возмущений) обладают следующими характеристиками.

1. Частота волны определяется собственной частотой атомного перехода. Иными словами, в общем случае, когда имеются группы атомов с частотами w _j, отличными от частоты поля накачки w , то в среде возникают волны с этими частотами w _j.

2. Волновой фронт волны поляризации содержит информацию о фронтах волн накачки /1/.

3. Фазовая скорость волны поляризации v_п=w _j/| _п| , где волновой вектор волны поляризации является функцией векторов накачки _п=¦ (₁₂₃…). Направление волны поляризации определяется направлением _п, а длина этого вектора | _п| задает скорость движения волны поляризации. Здесь сразу же намечается интересная ситуация, которая невозможна при одновременном взаимодействии. А именно, волна поляризации в системах с фазовой памятью может существовать самостоятельно без наличия в это время в среде бегущих направленных электромагнитных волн. Это следует из того, что в промежутках между импульсами (поля накачки отсутствуют), если соответствующим выбором направлений ₁, ₂, ₃… мы формируем _п такой длины, что

- 8 -

не будет выполняться условие фазового синхронизма, колебания отдельных диполей будут уже генерировать парциальные электромагнитные волны, которые не могут сфазироваться, и их интерференция не приведет к появлению бегущей направленной электромагнитной волны. Поэтому из всех волн только те волны поляризации, для которых выполняется условие v_n=с/n, где с - скорость света в вакууме; n - показатель преломления, генерируют направленные электромагнитные волны.

4. Волны поляризации со временем распадаются из-за наличия релаксационных процессов. Например, в случае, если система атомов уширена однородным образом (имеется лишь одна группа атомов с частотой w _j), то амплитуда волны поляризации затухает по закону pexp[-Гt], где Г- полуширина линии. Формирование волн поляризации можно качественно изучить на самой простой ситуации (импульсы накачки очень коротки, т.е. можно не учитывать релаксацию и расфазировку во время действия импульса, система однородно уширена, т.е. имеем одну изохромату w _j, и промежутки между импульсами гораздо меньше времени поперечной релаксации). В этом случае действие на регистрирующую среду оптического импульса с вектором , напряженностью поля e частотой w , временем подачи t₀ приводит к возникновению волн поляризации вида:

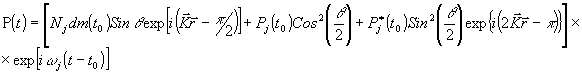(1)

где t > t₀; n_j - концентрация диполей; d - дипольный момент перехода; q = dħ^{-1e d} t; d t- длительность прямоугольного импульса накачки; m(t₀) , p_j(t₀) - инверсия и поляризация, которые имелись в среде в момент подачи импульса накачки. Инверсия и поляризация тесно связаны друг с другом и сообща определяют эволюцию системы при многоимпульсном возбуждении. Поэтому необходимо рассматривать также изменение инверсии под действием импульса накачки

- 9 -

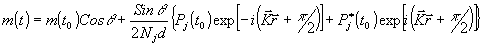(2)

Поэтапное использование этих формул при многоимпульсной накачке позволяет проследить за эволюцией системы, за рождением и уничтожением волн поляризации и решеток населенностей уровней, за перекачкой степени возбуждения из одной волны в другую и т.п. Общие закономерности ясны из анализа этих выражений. Во-первых, если накачка действует в момент, когда уже произошло полное затухание волн поляризации, т.е. Р_j(t₀) = 0, то в (1) остается только первое слагаемое. Если среда однородна, т.е. m(t₀) ¹ f(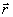), то в среде генерируется лишь одна волна поляризации, которая удовлетворяет условию фазового синхронизма, но отстает от волны накачки на p /2.

Если же среда была неоднородна, например, m(t₀) имеет вид периодической решетки с вектором d , то первый член (1) генерирует три волны поляризации с векторами , ± d . В насыщенной системе, т.е. при m(t₀) = 0, вообще ничего не происходит, если p_j(t₀) = 0.

Во-вторых, из (1) видно, что любая волна поляризации с комплексной амплитудой p_j = a_jexp[i_n·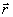], которая имеется в среде к моменту t₀, служит источником двух волн поляризации. Второй член выражения (1) при этом характеризует изменение амплитуды прежней волны поляризации (донорной), без изменения ее скорости и направления. Более интересен третий член, который является результатом интерференции атомных суперпозиционных состояний и характеризует рождение новой волны поляризации с комплексносопряженной амплитудой. Эта волна сдвинута по фазе на l /2 по сравнению с прежней волной, амплитуда ее зависит от степени истощения донорной волны, а скорость и направление зависят от волнового вектора этой волны ’_n = 2 - _n. .В течение времени действия импульса накачки (q ~ t) происходит взаимная перекачка энергии из донорной волны поляризации в интерференционную и обратно. В случае, когда импульс накачки является не бегущей волной, а стоячей (при = 0), то, как видно из третьего

- 10 -

слагаемого (1), происходит рождение обращенной со всем параметрам волны. Поведение когерентной инверсии, которая определяет разность населенностей уровней перехода, а, следовательно, основные оптические параметры среды, также связаны с наличием в среде остаточной поляризации. Например, если в среде имелась лишь одна волна поляризации a_jexp[i_n·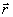], то, как следует из (2), инверсия после действия волны накачки с вектором будет иметь вид пространственной решетки с вектором ( - _n). Соответственно, при наличии нескольких волн поляризации формируется такое же количество решеток инверсии. Количество решеток растет нелинейно с увеличением числа импульсов накачки и после действия импульсов число решеток можно в общем случае определить по формуле

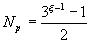(3)

Количество волн поляризации, в свою очередь, после x - импульсного возбуждения равно 3x ^-1. Например, после действия четырех импульсов возникнет 27 волн поляризации и 13 решеток. Количество волн поляризаций и решеток на самом деле может быть гораздо меньше при определенных условиях возбуждения. Рассмотрим примеры.

1. Возбуждение последовательностью 2p - импульсов. Как следует из выражений (1) и (3), при q = 2p не происходит никаких изменений в системе. Это связано с тем, что 2p - импульс возбуждает систему в суперпозиционное состояние, а затем переводит ее обратно в первоначальное.

2. Накачка последовательностью p -импульсов. В этом случае волны поляризации не образуются, т.к. Р_j(0)= 0О, sinq _1,2,3 = 0, решетки также не формируются, а после каждого импульса система инвертируется, т.к. Соsq _1,2,3 = -1. Такое поведение системы обусловлено тем, что при такой накачке она вообще не попадает в суперпозиционное состояние к моменту окончания импульса.

3. Первый импульс переводит систему в суперпозиционное состояние с максимальным дипольным моментом, а последующие импульсы инвертируют систему (q ₁ = p /2, q ₂ = q ₃ = q ₄ = … = p ). Как следует из анализа (1) и (2), при таком возбуждении система насыщена

- 11 -

(m = 0), решеток не формируется (sinq _2,3,4 = 0), а в среде генерируется только одна интерференционная волна поляризации (третий член в выражении (1)). После каждого импульса накачки происходит изменение направления этой волны и ее скорости при сохранении одного и того же значения амплитуды

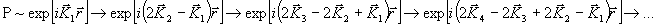
Соответствующим выбором направлений волн накачки для удовлетворения синхронизма эту волну на каждом этапе можно обнаружить по генерируемой ей электромагнитной оптической волне.

Интересно отметить еще одно свойство интерференционной волны, основанное на комплексной сопряженности ее комплексной амплитуды. Эти волны генерируются со сменой знака начальной фазы (см. выражение (1)). Поэтому после действия импульса накачки, когда волна поляризации имеет вид exp[w _j(t – t₀), набег фазы положителен, т.к. t > t₀, и происходит компенсация начального отрицательного значения фазы. Эта компенсация происходит в определенный момент времени вне зависимости от значения собственной частоты диполей, образующих данную волну поляризации. Это заключение позволяет понять очень важное явление, которое имеет место при возбуждении неоднородноуширенной системы атомов, т.е. в наиболее часто изучаемой практической ситуации. При накачке такой системы в каждом из вытекающих из (1) направлении будут распространяться уже несколько волн возмущений, генерируемых на разных изохроматах линии поглощения перехода. Эти волны имеют слегка отличную скорость распространения (если частоты w _j мало отличаются), а также начальный разброс по фазам. Так как после действия импульса компенсация этого разброса для всех изохромат происходит в одно и то же время, это приводит к сфазированию колебаний всех групп и возникновению сверхполяризации, которая служит источником поля фотонного эха /2/.

Таким образом, из рассмотренных здесь наиболее простых ситуаций неодновременного возбуждения систем с фазовой памятью видно, что волновая связь между оптическими волнами накачки осуществляется через материальные волны возмущения, формируемые

- 12 -

в среде, при их тесной взаимосвязи с когерентной инверсией атомных состояний. При этом взаимодействие определяется уже не столько когерентностью полей накачки, сколько когерентностью суперпозиционных состояний, в которые переведена атомная система. Подтверждением этого является продемонстрированная в /3/ возможность формирования интерферограммы в такой среде при помощи пучков света, разнесенных на время, гораздо большее длины когерентности источника света. Например, в рубине решетка индуцировалась при интервале между импульсными пучками накачки равном 50 нс (при длительности импульсов ~ 10 нс), в то время как измеренная обычным способом по видности интерференционной картины длина когерентности применяемого лазерного излучения составляла не более одного метра.

Отсюда следует очень важный вывод о необходимости учитывать определяющую роль фазовой памяти регистрирующей среды при записи в этой среде интерференционных картин.

Литература

1. Е.И.Штырков. Динамические голограммы на суперпозиционных состояниях атомов. В кн. "Голографические методы исследований", Л., ЛИЯФ, 118-130, 1978; Оптика и спектроскопия, 45, 603, 1978; Динамическая эхо-голография. В кн.: "Голография и оптическая обработка информации: методы и аппаратура". Л., ЛИЯФ, 188-203, 1960.

2. i.abella, n.kurnit, s.hartnbn, Рhys.rev., 141, 391, 1966.

3. Е.И.Штырков, В.С.Лобков, Н.Г.Ярмухаметов. Письма в ЖЭТФ, 27, 685, 1978.