|
|
 |
 |

|
| |
О ВОЗМОЖНОСТИ ИЗМЕРЕНИЯ ТЕМПЕРАТУРНОГО КОЭФФИЦИЕНТА ЛИНЕЙНОГО РАСШИРЕНИЯ АНИЗОТРОПНЫХ И ИЗОТРОПНЫХ МАТЕРИАЛОВ МЕТОДОМ ГОЛОГРАФИЧЕСКОЙ ИНТЕРФЕРОМЕТРИИ
Б.В.Федулеев, В.П.Рябухо, В.Б.Рабкин
Анализируется интерференционная картина, формируемая голографическим интерферометром, в котором 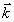 = const для всех точек поверхности исследуемого объекта для случая жесткого смещения и однородной температурной деформации объекта. Показано, что изучение пространственного распределения интенсивности света по поверхности объекта позволяет экспериментально определить термический коэффициент линейного расширения анизотропных и изотропных материалов. Полученные экспериментальные результаты измерения термического коэффициента линейного расширения для образца, изготовленного из изотропного материала, хорошо согласуются с табличными данными. = const для всех точек поверхности исследуемого объекта для случая жесткого смещения и однородной температурной деформации объекта. Показано, что изучение пространственного распределения интенсивности света по поверхности объекта позволяет экспериментально определить термический коэффициент линейного расширения анизотропных и изотропных материалов. Полученные экспериментальные результаты измерения термического коэффициента линейного расширения для образца, изготовленного из изотропного материала, хорошо согласуются с табличными данными.
В работе /1/ исследовалась возможность применения метода двух-экспозиционной голографической интерферометрии для измерения температурного коэффициента линейного расширения (ТКЛР) изотропных материалов.
В настоящей работе развиваются изложенные в /1/ идеи и приемы с целью разработки методики измерения ТКЛР анизотропных и изотропных материалов, а также упрощения методики прямых измерений по интерферограммам и повышения точности метода.
Для анализа голографических интерферограмм в настоящей работе использовалось известное соотношение:
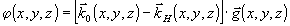 , (1) , (1)
где 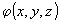 - разность фаз между световыми волнами, рассеянными идентичными точками с координатами x,y,z; - разность фаз между световыми волнами, рассеянными идентичными точками с координатами x,y,z;
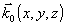
и 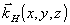 - волновые векторы световых волн, соответственно, освещающей объект и рассеянной в направлении наблюдения; - волновые векторы световых волн, соответственно, освещающей объект и рассеянной в направлении наблюдения;
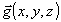
- вектор смещения рассматриваемой точки поверхности.
В силу того, что при изменении температуры объект, кроме температурного расширения, может совершать поступательное и вращательное движение, вектор 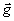 , при условии малости этих смещения, представим в следующем виде: , при условии малости этих смещения, представим в следующем виде:
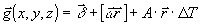 , (2) , (2)
где 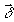 - вектор поступательного смещения; - вектор поступательного смещения; 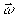 - вектор вращения объекта; - вектор вращения объекта;
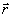 - -
радиус-вектор рассматриваемой точки объекта;
А - матрица теплового расширения;
Δ - разность температур объекта между двумя экспозициями,
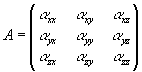 . (3) . (3)
При освещении объекта плоской волной и наблюдении интерферограммы с расстояния, значительно превышающего размеры объекта, вектор 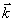 является медленно меняющейся функцией координат. Поэтому при наличии незначительных смещений анализ можно проводить в предположении, что вектор является медленно меняющейся функцией координат. Поэтому при наличии незначительных смещений анализ можно проводить в предположении, что вектор 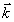 =const для всех точек поверхности исследуемого объекта ( =const для всех точек поверхности исследуемого объекта (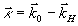 ). ).
Выберем прямоугольную систему координат так, чтобы ось была параллельна биссектрисе угла между направлениями освещения и наблюдения, а направление осей х, у и положение начала координат произвольны. Подставляя (2) и (3) в (1) и принимая во внимание, что вектор 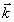 параллелен оси z и постоянен для всех точек поверхности объекта, получаем параллелен оси z и постоянен для всех точек поверхности объекта, получаем
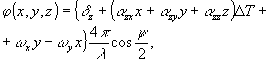 (4) (4)
где λ - длина волны излучения, используемого при голографировании;
δ z - проекция вектора 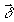 на ось z; на ось z;
ω x, ωy - проекции вектора 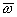 на оси x и у, соответственно, на оси x и у, соответственно,
Ψ - угол между направлениями освещения и наблюдения;
α zx, αzy, αzz - элементы матрицы (3).
Формула (4) выражает зависимость разности фаз φ от координат точек поверхности. Так как интенсивность интерференционной картины есть периодическая функция разности фаз φ, то (4) фактически описывает пространственное распределение интенсивности по поверхности объекта. В (4) отсутствует составляющая вектора 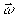 на ось z, то есть голографический интерферометр в случае на ось z, то есть голографический интерферометр в случае 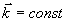 не зарегистрирует интерференционную картину при вращении объекта вокруг оси, параллельной биссектрисе угла между направлениями освещения и наблюдения. не зарегистрирует интерференционную картину при вращении объекта вокруг оси, параллельной биссектрисе угла между направлениями освещения и наблюдения.
Поскольку на пространственное распределение интенсивности света в интерференционной картине будут оказывать влияние только члены, зависящие от x, y и z, то можно сделать вывод, что в зарегистрированной интерференционной картине не будет содержаться информации о поступательном смещении. Нечувствительность рассматриваемого интерферометра к этим смещениям позволяет просто и наглядно интерпретировать интерференционную картину, рассматривая характер распределения интенсивности света по поверхности объекта. Наблюдаемую интерференционную картину удобно представить как результат пересечения с поверхностью объекта некоторого воображаемого интерференционного поля, которое будет описываться выражением (3), если не накладывать ограничений на область задания переменных x, у, z. В силу линейности выражения (4) распределение интенсивности в интерференционном поле должно характеризоваться постоянной пространственной частотой. Покажем, что знание пространственных частот этого распределения позволяет определить компоненты вектора 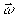 и элементы матрицы А. и элементы матрицы А.
Пространственные частоты интерференционной картины опре-
деляются как деленные на 2π пространственные скорости изменения фазы φ (x,у,z) по соответствующим направлениям.
Измеряемыми параметрами интерференционной картины являются пространственные периоды, определенные как величины, обратные пространственным частотам. Выражая пространственные частоты ξ x, ξy и ξz через пространственные периоды Λx, Λу, Λz, соответственно, и используя (4), можно получить выражение:
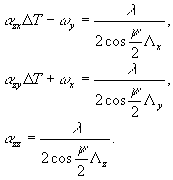 (5) (5)
Изменяя направления наблюдения, можно получить достаточное число уравнений вида (5) для определения всех элементов матрицы А через пространственные периоды интерференционных картин, наблюдаемых с этих направлений.
Для случая изотропного материала система уравнения (5) преобразуется следующим образом:
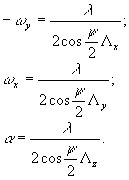 (6) (6)
Из (6) следует, что для расчета ТКЛР изотропного материала достаточно информации, получаемой с интерферограммы, наблюдаемой с одного направления, необходимо лишь отмерить пространственный период интерференционной картины в направлении, сов-
падающем с биссектрисой угла между направлениями освещения и наблюдения.
Если известны собственные направления матрицы А (определяются с помощью рентгено-структурного анализа), то задача нахождения элементов матрицы сводится, в общем-то, к изотропному случаю.
Действительно, если принять за оси координат эти собственные направления, то матрица А примет диагональный вид:
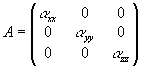 . (7) . (7)
Если направление вектора 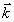 совпадает с направлением одной из этих осей, например z, то система уравнений (5) преобразуется следующим образом: совпадает с направлением одной из этих осей, например z, то система уравнений (5) преобразуется следующим образом:
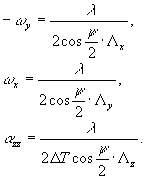 (8) (8)
Аналогичные уравнения могут быть получены для αхх и αуу (регистрируем интерферограммы с направлений, когда 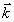 || оси X и || оси X и 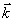 || оси Y). || оси Y).
Расчетные формулы для определения ТКЛР изотропного (6) и анизотропного (8) материалов подобны. Поэтому, не нарушая общности рассуждений, рассмотрим методику определения пространственного периода и ТКЛР по наблюдаемым интерферограммам на примере изотропного материала.
Для упрощения интерпретации интерференционной картины будем рассматривать только линии, в которых интенсивность макси-
мальна, то есть центры светлых полос, где φ=2πm (m - порядок интерференции). Эти линии являются следами сечения поверхности объекта воображаемой системой параллельных плоскостей. Очевидно, что соответствующие пространственные периоды этой системы плоскостей будут равны Λx, Λy, Λz. Искомый пространственный период Λz есть расстояние между соседними плоскостями в направлении оси z, которое можно определить по формуле:
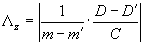 , (9) , (9)
где m и m'- порядки интерференции, соответствующие рассматриваемым плоскостям;
D и D' - свободные члены в уравнениях этих плоскостей, записанных в общем виде;
С - проекция нормального вектора плоскости m (или m') на ось L.
Подставляя (9) в (6), получим расчетную формулу для определения ТКЛР:
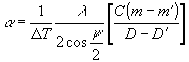 . (10) . (10)
В качестве параметров интерференционной картины в (10) выступают величины D, D' и С, которые могут быть определены различными способами в зависимости от формы поверхности объекта.
В самом обвей случае эти параметры можно рассчитывать, если для каждой из плоскостей m и m' известны координаты трех точек, принадлежащих поверхности объекта и не лежащих на одной прямой. Координаты этих точек могут быть измерены непосредственно по голографическому изображению, например, по методике, изложенной в работе /3/.
Точность определения α по формуле (10) зависит в основном от погрешностей измерения угла ψ и пространственного периода Λz. Первая погрешность минимальна, если
ψ=0[ 4], то есть в случае применения схемы голографического интерферометра с совпадением направлений наблюдения и освещения. В этой схеме реализуются также максимально возможная чувствительность, удобное освещение и наблюдение объекта. Погрешность измерения Λz, которая, в свою очередь, определяется в основном погрешностями прямых измерений по интерферограмме, также может быть уменьшена, если каждую из величин D, D', и С определять не по трем точкам, а интерполировать по n точкам.
Измерение координат точек поверхности объекта по его голографическому изображению является трудоемкой работой. Но для ряда объектов, поверхность которых ограничена плоскими поверхностями, операция измерения координат точек может быть заменена более простой и точной измерительной операцией. Поэтому в настоящей работе экспериментальные исследования проходились на образце специальной формы, что позволило производить прямые измерения по негативу интерферограммы.
Объект исследования представляя собой цилиндрический стержень с четырехгранным пирамидальным торцом. Грани пирамиды располагались под одинаковым углом β к оси цилиндра.
Регистрация интерферограмм осуществлялась в голографическом интерферометре с совпадением направлений освежения и наблюдения. Объект в термостате устанавливался таким образом, чтобы он освещался со стороны пирамидального торце, а направление освещения было параллельно оси цилиндра. Выполнение этого условия обеспечивалось применением специального юстировочного элемента, который представлял собой цилиндрический стержень диаметром 5 мм с плоским зеркально отражавшим торцом, расположенным перпендикулярно оси стержня. Образец и юстировочный элемент располагались в термостате так, чтобы их оси были параллельны - тем самым задавалась необходимая ориентация образца в голографической схеме.
На рис.1а изображено сечение образца плоскостью XOZ, проходящей через вершину пирамиды и биссектрисы плоских углов противоположных граней. Ось z совпадает с направлениями, освещения и наблюдения. Прямые m1, m2, m3... являются линиями пересечения воображаемой системы плоскостей с плоскостью XOZ.
Предполагается, что объект, кроме изотропного расширения, совершил вращательное движение вокруг оси Х. Схематичный вид наблюдаемой интерференционной картины изображен на рис.1б, где для простоты представлены только линии максимальной интенсивности.
Принимая во внимание, что регистрируемое фотокамерой изображение объекта является проекцией реального объекта на плоскость, перпендикулярную направлению регистрации рис.2, из рис.1а нетрудно установить аналитическую зависимость между наблюдаемыми пространственными периодами Λ 1, Λ2 и искомым периодом Λz. Эта зависимость имеет вид:
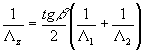 . .
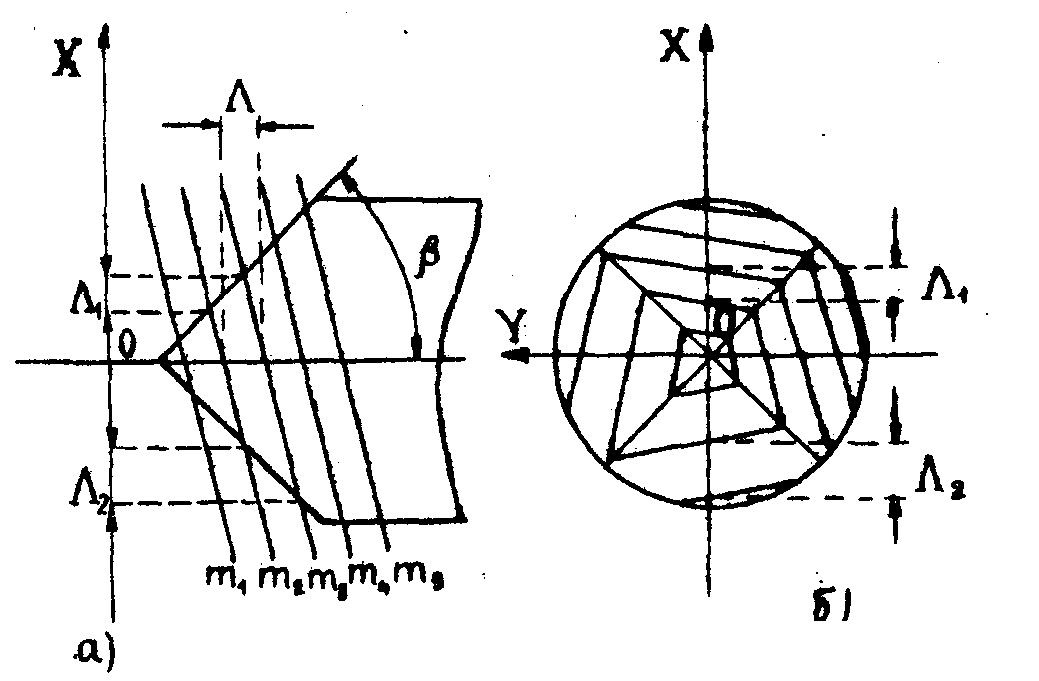
Рис.1. К выводу формулы (11).

Рис.2. Интерферограмма исследуемого образца.
Подставляя (11) в (10) и учитывая масштаб фотографирования ρ, получим расчетную формулу для образца выбранной формы:
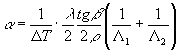 . .
Таким образом, операция измерения координат точек поверхности объекта фактически заменена более простыми операциями измерения угла β и величин Λ1 и Λ2.
Величины Λ 1 и Λ2 измерялись по негативу интерферограмм на компараторе ИЗА-2, причем наводка на середину полос осуществлялась не центром перекрестия окуляра, а одной из его линий, что на порядок повысило точность этих измерений. Относительная погрешность α, обусловленная погрешностями измерения Λ1 и Λ2, составила 1.5%. Относительная погрешность измерение угла β составила 0,5%. В качестве остальных источников погрешностей метода следует отметить: некоторую чувствительность схемы к жесткому смещении (эта погрешность зависит от величины смещения и в наших экспериментах составила 0,1%), неточность выбора направления регистрации интерферограммы (0,2%), неточность определения масштаба фотографирования (0,1%).
Была проведена серия измерении ТКЛР меди в интервале температур 20°С - 140°С. Величины ТКЛР, рассчитанные по полученным интерферограммам, находились, в соответствии с табличными данными, в пределах ожидаемых погрешностей метода. На рис.2 приведен фотоснимок интерферограммы, полученной при ΔТ=6°С, Тср =78°С. Рассчитанное значение α составляло 1,73∙10-5 град-1.
Заключение
Проведенный расчет и экспериментальные исследования позволяют сделать следующие выводы:
1. Анализ интерферограмм, формируемых в двухэкспозиционном голографическом интерферометре с 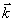 =const для всех точек поверхности исследуемого объекта, в результате жесткого смешения и однородной деформации исследуемого объекта целесообразно производить на основе изучения пространственного рас- =const для всех точек поверхности исследуемого объекта, в результате жесткого смешения и однородной деформации исследуемого объекта целесообразно производить на основе изучения пространственного рас-
пределения интенсивности света по поверхности объекта. Интерференционная картина в этом случае интерпретируется как результат пересечения поверхности объекта некоторым воображаемым интерференционным полем.
2. Проведенные (экспериментальные измерения ТКЛР по методике, разработанной для образца, изготовленного из изотропного материала, с поверхностью, ограниченной плоскостями, показали хорошее совпадение полученных результатов с табличными данными.
Авторы приносят искреннюю благодарность И.С.Клименко за внимание к работе и ценные замечания, сделанные им при чтении рукописи.
Л и т е р а т у р а
1. Хефлингер Л., Вуркер Р., Шпетцлер Н. Измерение методом голографической интерферометрии коэффициента теплового расширения объектов с диффузно отражающей поверхностью. Приборы для научных исследований, №5, с.101, 1973.
2. Корн Г., Корн Т. Справочник по математике. М."Наука", с.79-80, 1973.
3. Курбатов В.М., Николаев Ф.Я., Павлыгин Г.И. Автоматическое измерение координат точек объекта по голографическому изображению. Метрология, №9, 1971.
4. Солодкин Ю.И. Голографический интерферометр как измерительный прибор. Автометрия, №5, с.64, 1973.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

