О ВОЗМОЖНОМ И НЕВОЗМОЖНОМ В ЦИФРОВОЙ ГОЛОГРАФИИ
В.А.Сойфер, М.А.Голуб, А.Г.Храмов
Проведен анализ предельных характеристик точности решения прямой и обратной задач цифровой голографии. Установлена связь предельной точности восстановления параметров объекта с характеристиками систем регистрации и цифровой обработки голограммы. Получены аналитические выражения и численные оценки предельной точности воспроизведения волновых фронтов в зависимости от погрешностей дискретного представления голограмм в ЭВМ.
1.
Введение
Цифровая голография за последние 10 лет привлекает внимание все большего числа исследователей: физиков, математиков и инженеров. Появился ряд обобщавших обзоров /1,2/ и монография /3/, отражающих современное состояние проблемы анализа и синтеза волновых полей на ЭВМ. Однако до сих пор оценки практических возможностей цифровой голографии являются самыми противоречивыми. Оптимисты (к которым причисляют себя и авторы этой статьи) считают, что цифровая голография в сочетании с физической позволит решить ряд важных научных и прикладных проблем из числа "неразрешимых". Скептики не без оснований указывают на весьма скромные практические успехи современной цифровой голографии и высказывают сомнения в их возможном росте. В указанной ситуации решающая роль принадлежит теории цифровой голографии, однако создание ее наталкивается на ряд принципиальных трудностей, связанных прежде всего с необходимостью перехода от качественных оценок, "хуже" или "лучше" к количественным критериям сравнения различных способов анализа и синтеза голограмм на ЭВМ, а также с необходимостью установить некоторые предельные значения этих критериев. Отчетливо осознавая безнадежность попытки построения в
настоящее время общей теории цифровой голографии, авторы попытались тем не менее в этой статье, сузив класс рассматриваемых задач, ввести требуемые количественные критерии и установить их предельные значения. Исследование предельных, характеристик точности синтеза голограмм на ЭВМ (прямая задача цифровой голографии) удалось провести для задач контроля оптических поверхностей и пространственной фильтрации оптических полей. Проведенное рассмотрение позволило указать границы параметров волновых фронтов допускающих синтез методами цифровой голографии. Исследование предельных характеристик точности восстановления изображений и их параметров (обратная задача цифровой голографии) выполнено для голограмм Френеля-Фраунгофера и голограмм фазовых объектов.
2.
Границы возможного для голограмм, синтезированных на ЭВМ
Уже первые исследователи /4/ обнаружили, что изображение, восстанавливаемое с машинной голограммы, имеет довольно низкое качество, иногда даже мало похоже на свое математическое описание. Чтобы понять причины таких неутешительных результатов, следует подробнее рассмотреть процесс получения машинной голограммы. При этом мы будем рассматривать погрешности, специфичные лишь собственно для машинных голограмм, не учитывая влияния регистрирующей среды и других факторов проявляющихся и в физических голограммах. Пусть требуется получить голограмму с функцией пропускания по амплитуде W(u,v)∙|u|≤d/2∙|v|≤d/2 (d -размер голограммы).
В ЭВМ хранятся лишь N´
N отсчетов голограммы
Гnm=Q
M[W(u
n,v
m)]; n,m=
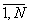
, (1)
получающиеся из "математической" голограммы
W(u,v) путем дискретизации по аргументам с шагом δ и квантования по М уровням (QM означает операцию квантования отсчета). Заметим, что величина θ есть разрешение машинной голограммы.
Величины
{Гn,m; n,m=
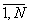
}
подаются в виде электрических сигналов на устройство регистрации голограмм, которое засвечивает N´
N ячеек на плоскости светочувствительного носителя с экспозицией, определяемой соответствующим отсчетом, или модулирует пучок когерентного света. Дискретизация кажется вполне "законной" операцией в силу известной теоремы отсчетов. Однако это верно лишь па первый взгляд. В действительности операции дискретизации ведут к появлению основных отличий машинных голограмм от физических голограмм и существенно ограничивают класс "реализуемых" волновых фронтов, которые можно восстановить с машинных голограмм с приемлемыми для практических приложений погрешностями.
Указать в общем случае класс реализуемых волновых фронтов не представляется возможным. Однако есть широкий класс задач, в которых волновой фронт, восстановленный с синтезированной голограммы, используется для количественных измерений и оптических вычислений. В этот класс входит оптическая пространственная фильтрация изображения, контроль оптических систем с помощью синтезированных голограмм и ряд других задач. В перечисленных задачах в явном виде присутствует не только математически заданная структура и форма волнового фронта, который нужно получить, но и количественный критерий точности его получения.
Рассмотрим задачу получения эталонного асферического волнового фронта
σ (см. рис.1). Пусть голограмма Г синтезируется так, чтобы при освещении ее пучком В (обычно сферическим или плоским) на заданном расстоянии должен восстанавливаться асферический волновой фронт σ. Вследствие конечного размера голограммы d, конечного разрешения голограммы δ, ограниченного числа отсчетов N=[d/δ] и уровней квантования М вместо волнового фронта δ восстанавливается лишь близкий к нему фронт 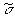 (см.рис.1). Максимальное (εmax) или среднеквадратичное (
(см.рис.1). Максимальное (εmax) или среднеквадратичное (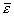 ) отклонение фронта
) отклонение фронта 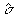 от σ и есть критерий точности синтезе голограммы Г. Величины εmax и ε зависят, во-первых, от параметров фронта σ (диаметр D, радиус кривизны
от σ и есть критерий точности синтезе голограммы Г. Величины εmax и ε зависят, во-первых, от параметров фронта σ (диаметр D, радиус кривизны
R
, степень асферичности и т.п.) и, во-вторых, от параметров устройства регистрации голограмм (разрешение δ или число отсчетов N, диаметр голограммы d, число уровней квантования М):
ε
max=εmax(δ,d,M;D,R,...)=εmax(N,d,M;D,R,...).
Если погрешность
εmax окажется слишком большой, то получить фронт σ с помощью голограммы Г невозможно. Таким образом, "область невозможного" в этой задаче задается соотношением
ε
max(N,d,M;R,D,...)≥εдоп, (2)
где
εдоп - допустимая максимальная погрешность. Для широких приложений εдоп=λ/5 (λ - δлина волны света).
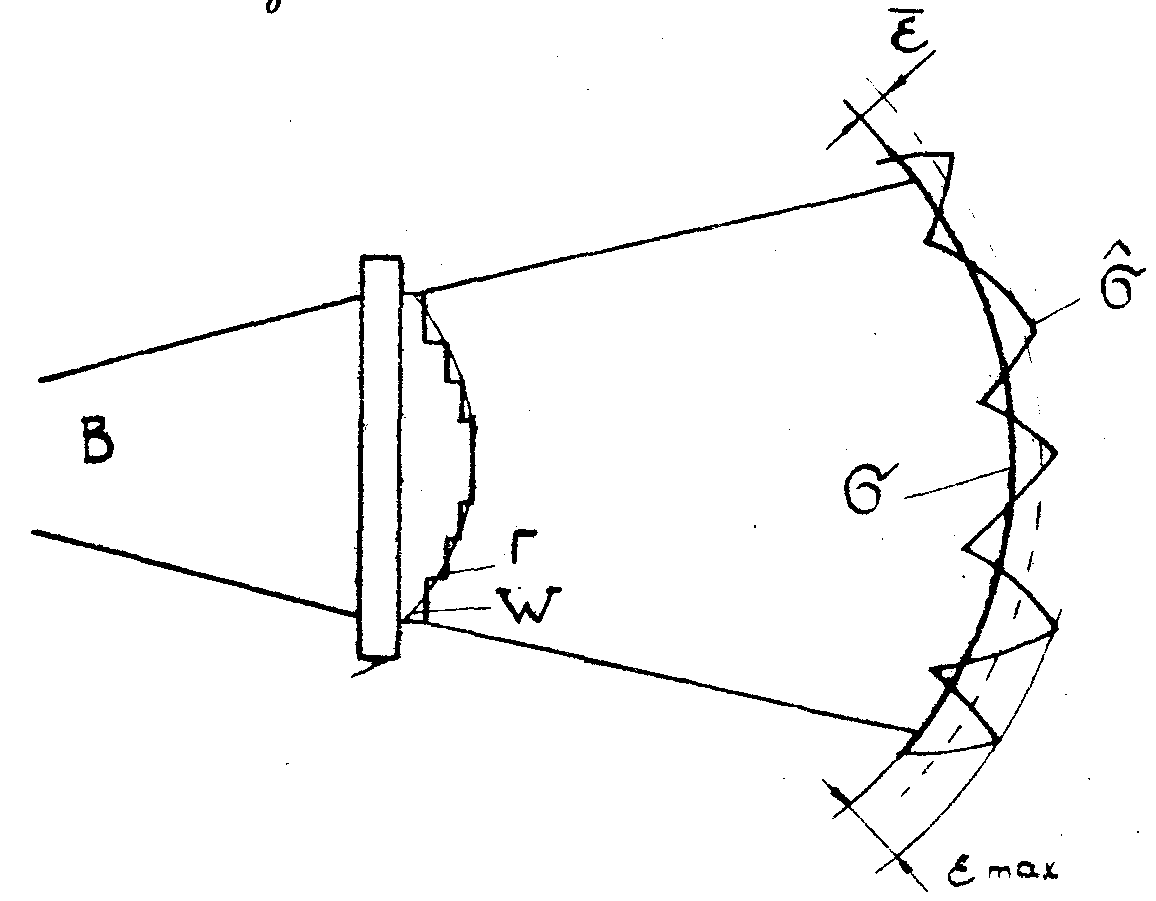
Рис.1. Получение эталонного волнового фронта с помощью синтезированной на ЭВМ голограммы.
В особо точных оптических приборах
εдоп=λ/10÷λ/100. Σравнение (2) при заданных характеристиках устройства регистрации машинных голограмм определяет некоторую область значении параметров фронта σ. Волновые фронты с параметрами из такой области не могут бить реализованы методами цифровой голографии (при использовании устройств с характеристиками N, d, M).
Пример 2.1
. Пусть восстанавливаюший фронт В сферический с центром О, удаленным на расстояние
R от вершины асферической поверхности σ, задаваемой уравнением
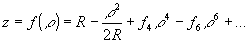 (3)
(3)
(см.рис.
2). Тогда можно показать, что точность εmax определяется по формуле
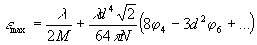 , (4)
, (4)
где
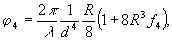 (5)
(5)
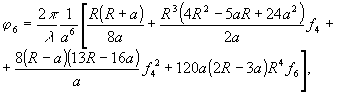 (6)
(6)
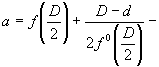 (7)
(7)
- расстояние от голограммы до точечного источника О сферической волны. В частности, для параболического волнового фронта с фокусным расстоянием
F0 имеем: R=2F0, f4=f6=... =0 и можно получить простую оценку:
 (8)
(8)
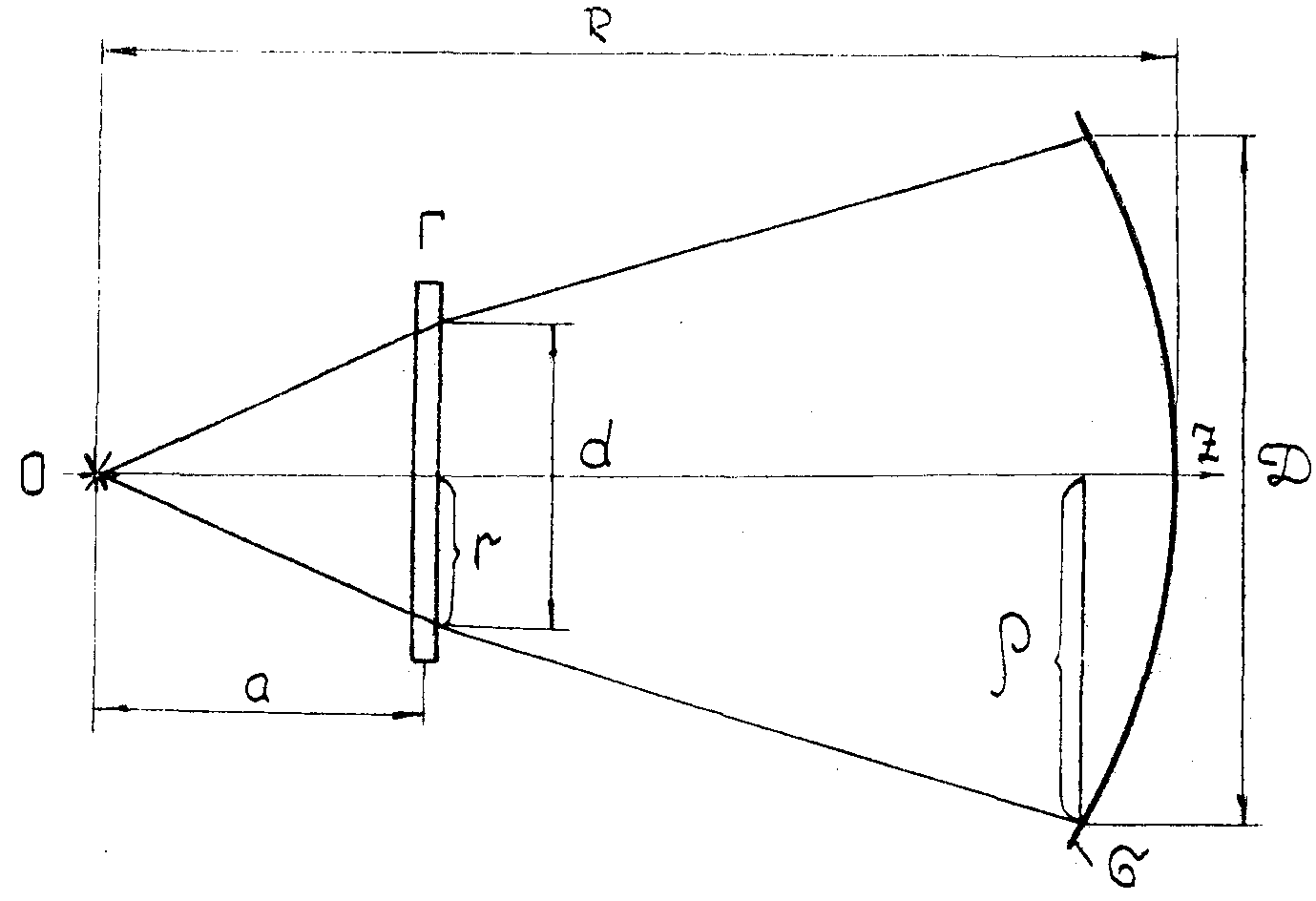
Рис.2. Преобразование сферического волнового фронта в асферический фронт.
Область невозможного (2) есть область значений параметров (
F0,D), для которых
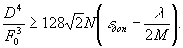 (9)
(9)
Границей области является кривая
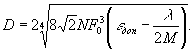 (10)
(10)
На рис.3 штриховкой изображена область значений фокусного расстояния F
0 и диаметра D фронта, которые невозможно реализовать с точностью εдоп=λ/20 методами цифровой голографии при использовании регистрации устройства голограмм с
N = 1024,
М = 256. Двойной штриховкой обозначена область, соответствующая εдоп = λ/5.
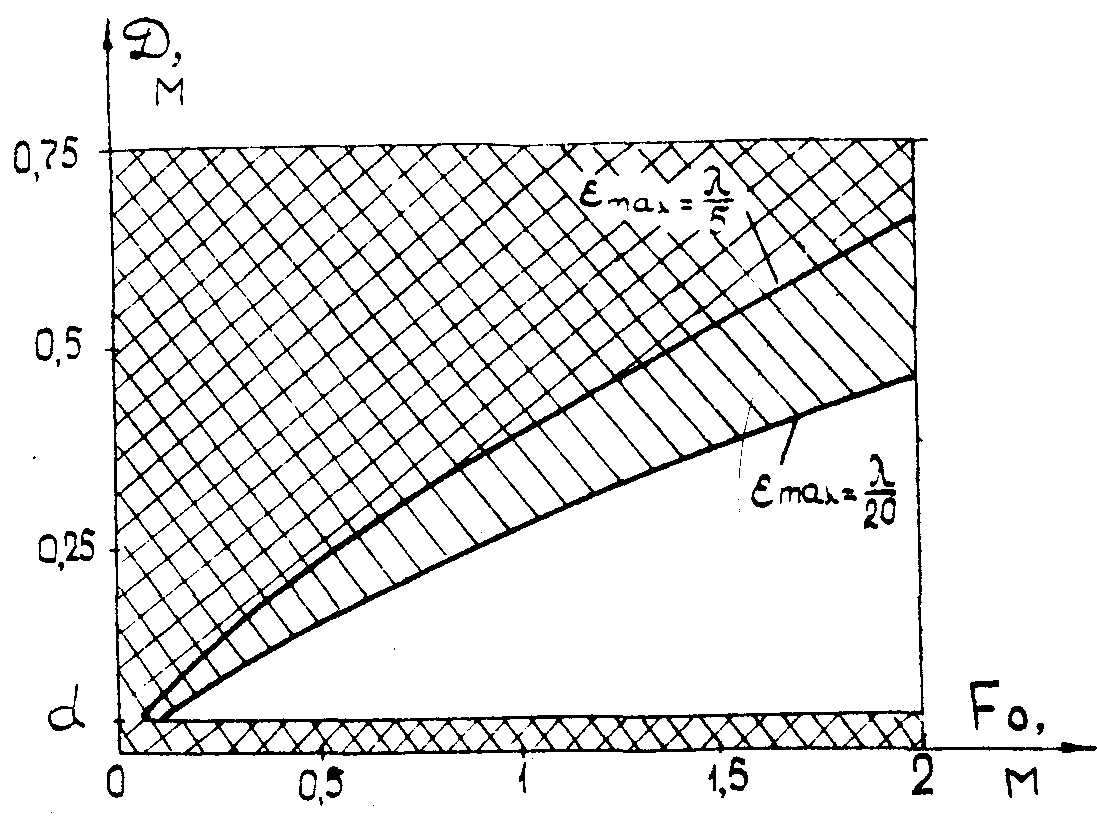
Рис.3. Область значений диаметра и фокусного расстояния параболического волнового фронта, которые невозможно получить с точностью λ/20 (штриховка) и λ/5 (двойная штриховка) из сферического волнового фронта при использовании устройства с числом отсчетов N = 1024 и уровней квантования М = 256.
Выбор устройства регистрации голограмм можно осуществить, пользуясь таблицей 1, в которой значения погрешности ε
max приведены в зависимости от разрешения δ=d/N, при различных диаметрах волнового фронта (выбрано F0 = 500 мм, d = 25,6 мм, М = 256, λ = 0,6328 мкм).
Таблица 1
|
δ
D |
50 мкм |
25 мкм |
12 мкм |
5 мкм |
1 мкм |
|
200 мм |
λ/4,5 |
λ/9 |
λ/18 |
λ/42 |
λ/160 |
|
300 мм |
λ/1, 5 |
λ/3 |
λ/6 |
λ/14 |
λ/65 |
Другая задача, в которой применяются синтезированные пространственные фильтры, - обобщенный спектральный анализ изображения ξ(х,у), |х
|≤A, |y|≤A, A=d/2, заключающийся в вычислении L первых коэффициентов
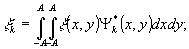
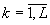 (11)
(11)
разложения изображения по ортонормированной системе базисных функции
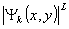 , (* - символ комплексного сопряжения).
, (* - символ комплексного сопряжения).
Применение ЭВМ, сопряженных устройствами регистрации, в принципе открывает возможность реализации в виде набора из синтезированных пространственных фильтров сложных базисных функций. Однако, вышеупомянутые погрешности дискретизации при синтезе фильтров на ЭВМ приводят к "возмущенным" базисным функциям
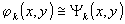 и погрешностям вычисления коэффициентов, т.е. фактически вместо (11) вычисляются "возмущенные" коэффициенты:
и погрешностям вычисления коэффициентов, т.е. фактически вместо (11) вычисляются "возмущенные" коэффициенты:
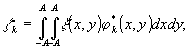
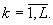 (12)
(12)
При неправильном выборе числа членов L в зависимости от характеристик устройства регистрации (N, М, А) и параметров изображения ξ(х,у) коэффициенты ζ
k будут настолько сильно отличаться от ξk, что придется отказаться от использования синтезированных на ЭВМ пространственных
фильтров. В качестве критерия точности синтезированных пространственных фильтров можно выбрать погрешность обобщенного спектрального анализа с помощью таких фильтров, а именно, величину Е среднеквадратичного отклонения от изображения ξ(х,у) отрезка из
L первых членов его ортогонального разложения. Заметим, что погрешность ε2 определяется уже не одной голограммой, а целым набором из L пространственных фильтров. Предельно достижимое минимальное значение погрешности ε2 обеспечивается оптимальным базисом Карунена-Лоэва. В работе /5/ показывается, что для базисных функций Карунена-Лоэва
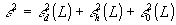 . (13)
. (13)
Компонента
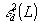 характеризует представление изображения конечным числом L обобщенных спектральных компонент при идеальной реализации базисных функций Карунена-Лоэва. Очевидно,
характеризует представление изображения конечным числом L обобщенных спектральных компонент при идеальной реализации базисных функций Карунена-Лоэва. Очевидно, 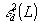 монотонно убывает с ростом L. При наличии дискретизации базисных функций погрешность ε2 больше, чем
монотонно убывает с ростом L. При наличии дискретизации базисных функций погрешность ε2 больше, чем 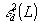 , а погрешности базисных функций накапливаются с ростом L и характеризуются величинами
, а погрешности базисных функций накапливаются с ростом L и характеризуются величинами 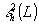 и
и 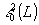 . Чрезмерное увеличение числа L при наличии неточно реализованных (дискретизированных) базисных функций не оправдано и ведет не к улучшению, а к ухудшению точности. Таким образом, при реализации базисных (пункций методами цифровой голографии невозможно получить точность, лучшую, чем
. Чрезмерное увеличение числа L при наличии неточно реализованных (дискретизированных) базисных функций не оправдано и ведет не к улучшению, а к ухудшению точности. Таким образом, при реализации базисных (пункций методами цифровой голографии невозможно получить точность, лучшую, чем 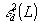 .
.
Пример 2.2
. Пусть изображение ξ(х,у) имеет биэкспоненциалъную корреляционную функцию
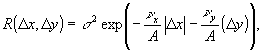 (14)
(14)
причем на размере
d изображения укладывается νх=νу=ν интервалов корреляции по осям х,у, соответственно.
На рис.4 приведены графита зависимости погрешности
ε2 от числа коэффициентов L при различном числе отсчетов пространственного фильтра, реализующего базисную функцию
(ν
х=νу=2,3). Пунктиром обозначено предельное значение точности, к которому можно приближаться при N
→∞. Из рис.4 видно, что при любом конечном N кривая ε2=ε2(L) имеет минимум в точке L=L0(N). Увеличивать L до значений больших, чем L0(N), нецелесообразно, т.к. из-за накопления погрешностей базисных пункций точность все равно не будет лучше, чем предельное значение ε2(L
0(N)).
С ростом числа отсчетов точка L0(N) отодвигается вправо, а предельно достигаемая погрешность ε2(L
0(N))
уменьшается. Одновременно с ростом N уменьшается и погрешность ε2 при каждом L .
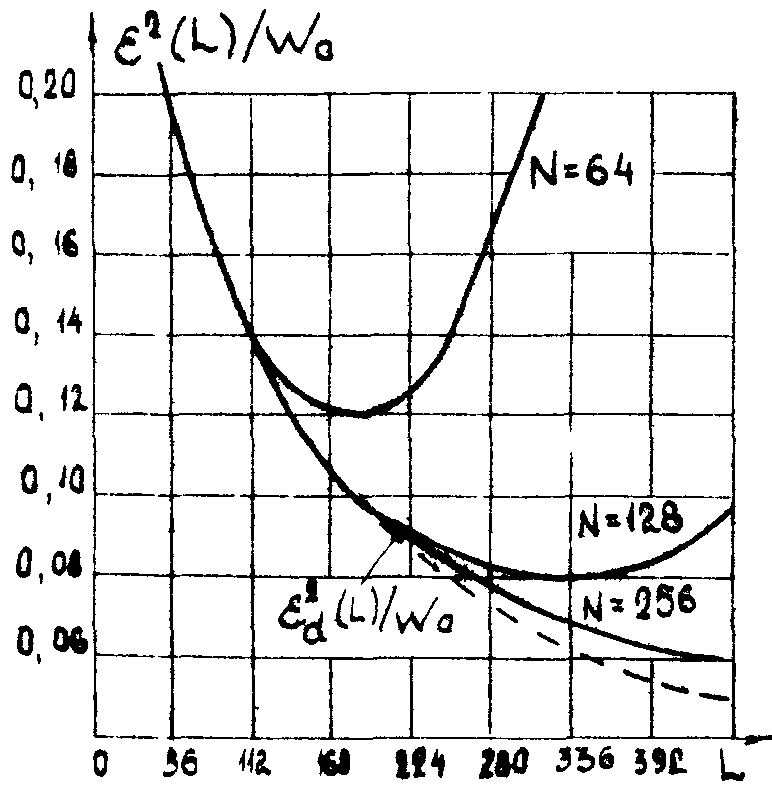
Рис.4. Среднеквадратичная погрешность обобщенного спектрального анализа изображения при реализации базисных функций в виде пространственных фильтров, синтезированных на ЭВМ.
В таблице 2 приведены значения
ε2 по отношению к полной энергии изображения W0 при L = 456, νх=νу=2,3 для различных чисел отсчетов
N.
Таблица 2
|
N |
128 |
256 |
512 |
1024 |
|
ε 2/W0 |
9,8% |
5,8% |
5,5% |
5,4% |
Таблица 2 и график рис.4 позволяют по заданному классу точности определить число отсчетов пространственного фильтра.
3.
Границы точности восстановления параметров объекта
по голограмме
Голографический эксперимент позволяет регистрировать комплексные поля и восстанавливать объект. В конечном счете исследователя интересуют либо параметры изучаемого объекта (например, геометрические размеры и координаты деталей изображения), либо собственно изображение объекта. Известно /6/, что на этапах регистрации и восстановления голограммы возникают случайные искажения, которые снижают точность измерения параметров изображения. В теории информации известны методы, позволяющие оценить предельную точность восстановления параметров для определенных моделей наблюдения /7,8/. Поэтому возникает проблема разработки моделей наблюдения сигналов, соответствующих различным схемам голографического процесса.
При оценивании точности измерения параметра "а" голографического изображения будем использовать среднеквадратичную ошибку
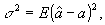 (15)
(15)
где Е - оператор усреднения,
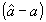 - погрешность измерения параметра.
- погрешность измерения параметра.
Точность измерения голографического изображения объекта
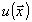 определяется выражением
определяется выражением
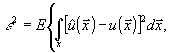 (16)
(16)
где
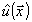 - постановленное в области
- постановленное в области 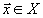 изображение объекта.
изображение объекта.
Будем использовать также относительные среднеквадратичные ошибки
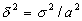 (17)
(17)
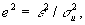 (18)
(18)
где
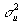 - дисперсия изображения
- дисперсия изображения 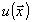 . Простейшая модель наблюдения имеет вид:
. Простейшая модель наблюдения имеет вид:
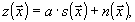
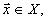 (19)
(19)
где а - неизвестная амплитуда сигнала,
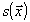 - детерминированная функция,
- детерминированная функция, 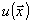 - белый гауссовский шум со спектральной плотностью мощности N0.
- белый гауссовский шум со спектральной плотностью мощности N0.
Среднеквадратичная ошибка оценки параметра "а" для модели
(19):
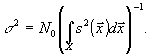 (20)
(20)
Если измеряемый параметр входит нелинейно в наблюдаемое поле, то модель имеет вид
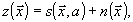
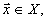 (21)
(21)
а точность восстановления имеет нижнюю границу, определяемую неравенством Крамера-Рао /
7/:
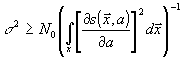 (22)
(22)
Если в (21) функция
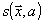 является случайной, то точность восстановления параметра "а" имеет следующую нижнюю границу /8/:
является случайной, то точность восстановления параметра "а" имеет следующую нижнюю границу /8/:
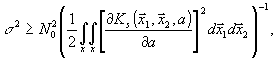 (23)
(23)
где
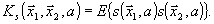 (24)
(24)
Соотношение (23) справедливо при
λ(0)<<N0, (25)
где
λ(ω) - энергетический спектр случайного сигнала 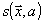 . Для модели наблюдения изображения
. Для модели наблюдения изображения
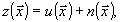
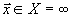 (26)
(26)
получаем
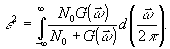 (27)
(27)
В (26) и далее полагается, что стационарное поле
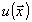 имеет энергетический спектр
имеет энергетический спектр 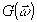 . Модель с линейными искажениями удобно записывать в спектральной области
. Модель с линейными искажениями удобно записывать в спектральной области
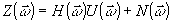 , (28)
, (28)
где
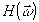 - передаточная функция искажающего фильтра. Среднеквадратичная ошибка для (28) определена в /9/:
- передаточная функция искажающего фильтра. Среднеквадратичная ошибка для (28) определена в /9/:
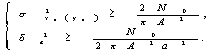 (29)
(29)
Если передаточная функция
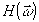 в модели (28) является случайной, то
в модели (28) является случайной, то
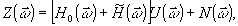 (30)
(30)
где
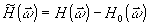 - случайная (неизвестная) составляющая пространственного фильтра.
- случайная (неизвестная) составляющая пространственного фильтра.
В
/10/ показано, что при определенных условиях ошибка восстановления для (30) имеет вид:
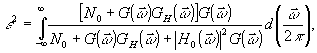 (31)
(31)
где
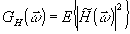 - энергетический спектр погрешности пространственного фильтра.
- энергетический спектр погрешности пространственного фильтра.
Заметим, что модель (30) можно использовать для описания процессов квантования и дискретизации при вводе в ЭВМ голограммы или голографического изображения.
Далее на примерах конкретизируем модели наблюдения, описанные выше, для некоторых схем голографического эксперимента.
Пример 3.1
. Применение голограмм Фраунгофера для измерения скоростей микрочастиц.
В /11/ описывается метод измерения средней скорости частиц по интерференционной картине в плоскости Фраунгофера, полученной при двойной экспозиции. Восстанавливаемая из голограммы дифракционная картина Фраунгофера имеет периодическую структуру, которая для одномерного гауссовского распределения скоростей имеет вид:
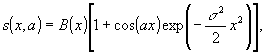 (32)
(32)
где а - измеряемая величина, пропорциональная средней скорости микрочастиц; σ
2 - дисперсия скоростей микрочастиц; В(х)- структурная функция, определяемая формой и ориентацией микрочастиц (для анализа полагаем B(x)=В ). Легко видеть, что (32) соответствует модели (21):
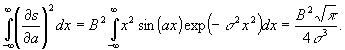 (33)
(33)
В (33) полагаем, что область анализа неограничена
(X→∞), а а/σ>>1, Используя (22) и (17), получаем
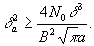 (34)
(34)
Заметим, что применение соответствующих методов обработки сигналов /7/ позволяет также оценивать и параметр
σ2.
Пример 3.2
. Оценка диаметра и координат центра частицы.
Интенсивность голографического изображения круглой частицы можно приближенно описать гауссовым пятном:
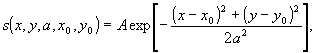 (35)
(35)
где а - диаметр частицы, (х
0,у0) -
координаты центра частицы. Используя (22), получим
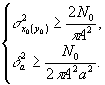 (36)
(36)
Заметим, что границы точности определения координат центра частицы не зависят от ее диаметра.
Пример 3.3. Мультипликативный шум.
Для простоты рассмотрим одномерную модель наблюдения частицы
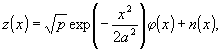 (37)
(37)
где φ(х) - случайная функция, описывающая мультипликативные шумы голографического процесса (например, диффузные шумы). Уравнение (37) совпадает с моделью (21) при случайном сигнале
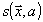 с корреляционной функцией (24) вида
с корреляционной функцией (24) вида
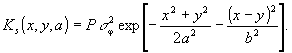 (38)
(38)
При а/
b>>1 из (22) и (38) получим
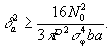 (39)
(39)
Заметим, что граница относительной среднеквадратичной ошибки обратно пропорциональна радиусу корреляции мультипликативных шумов.
Пример 3.4. Точность восстановления изображений.
Определим среднеквадратичную погрешность при наблюдении изображения на фоне аддитивного шума: модель (26). Будем рассматривать три наиболее распространенных класса изображений, соответствующих следующим корреляционным функциям: 1) биэкспоненциальная; 2) экспоненциальная изотропная; 3) гауссовская
изотропная.
Используя (16) и (18), получаем:
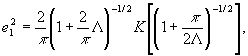 (40)
(40)
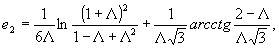 (41)
(41)
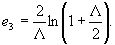 (42)
(42)
Здесь Λ - отношение сигнал/шум;
K(∙) - полный эллиптический интеграл первого рода. Зависимости (40),(41),(42) приведены на рис.5.
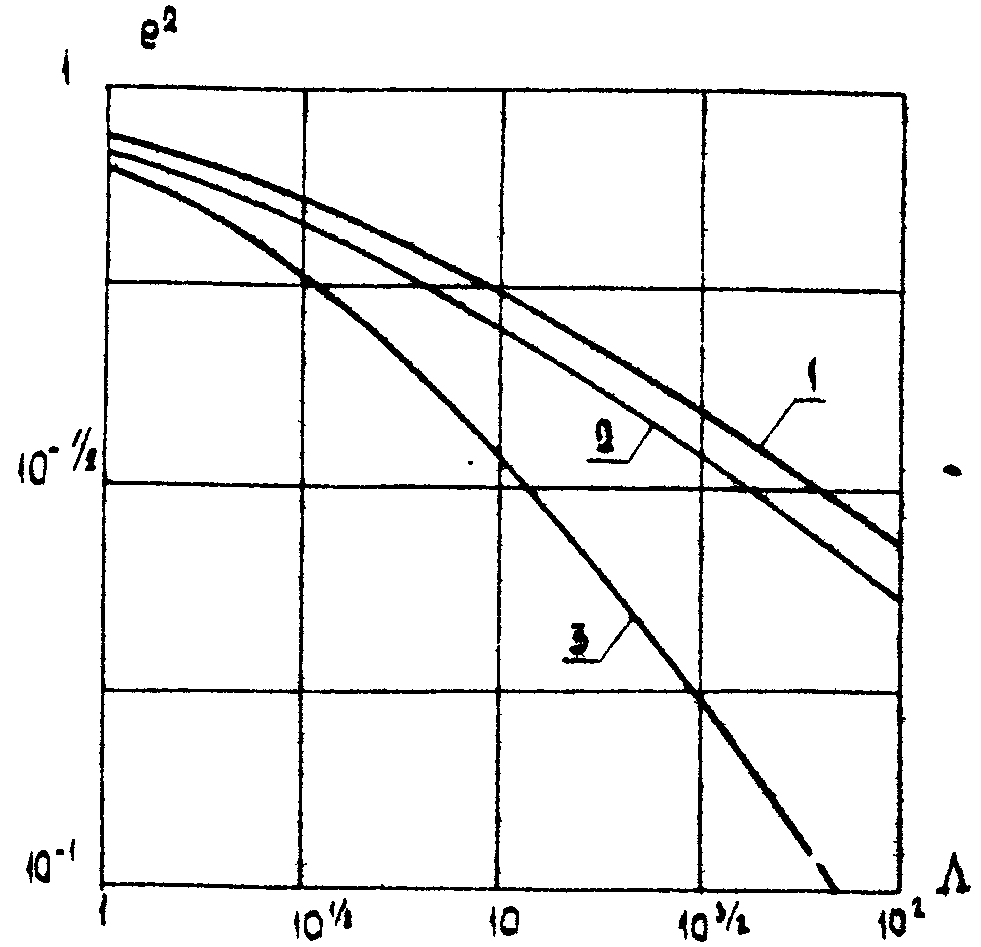
Рис.5. Граница среднеквадратичной погрешности восстановления
изображений с корреляционными функциями: 1 - биэкcпоненциальной, 2 - экспоненциальной изотропной, 3 - гауссовcкой изотропной.
В заключение получим границу точности восстановления голографических изображений с гауссовской изотропной корреляционной функцией с радиусом корреляции 1/α с учетом ограниченного углового размера 2Ω голограммы Фраунгофера. Из (29) получаем
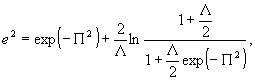 (43)
(43)
где
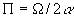 - приведенный размер голограммы. Ошибка (43) показана на рис.6.
- приведенный размер голограммы. Ошибка (43) показана на рис.6.
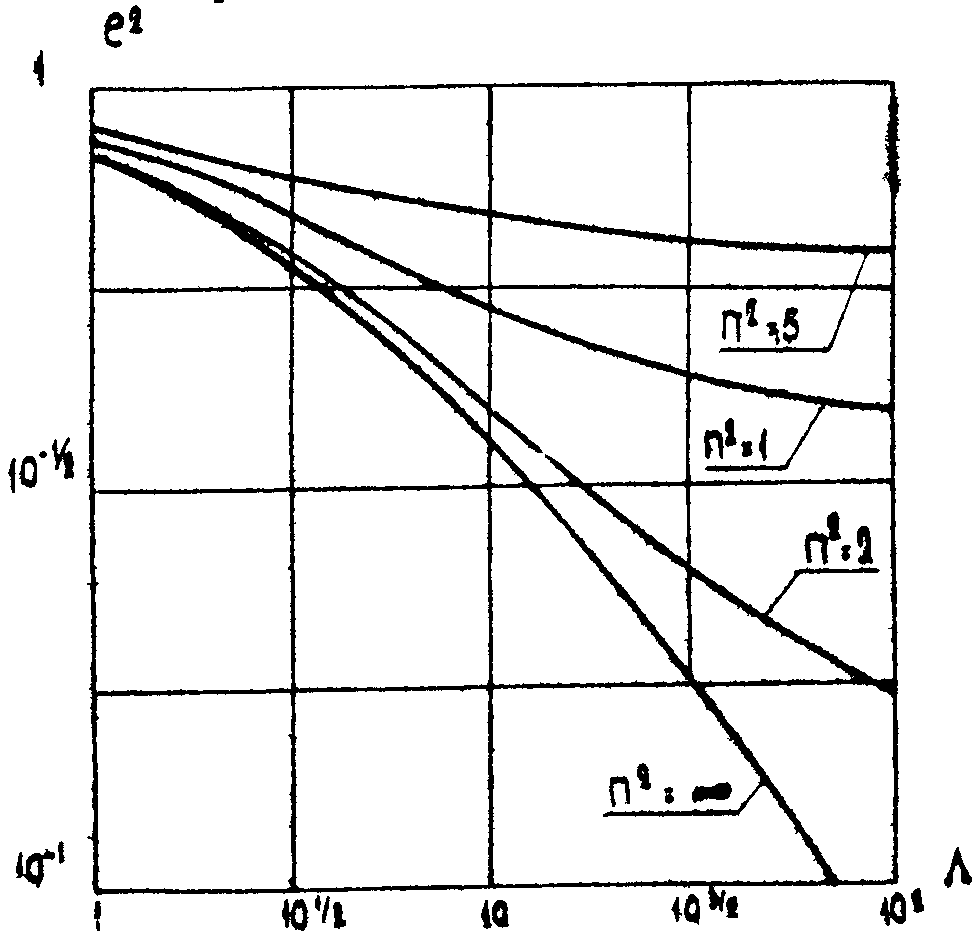
Рис.6. Граница среднеквадратичной погрешности восстановления изображений при ограниченных размерах голограммы.
4.
Заключение
Дальнейшие исследования предельных характеристик точности решения прямой и обратной задач и границ возможного и невозможного в цифровой голографии представляются наиболее актуальными в следующих направлениях:
1. Расширение сферы исследуемых прикладных задач: визуализации, адаптивной пространственной фильтрации, оптических систем обнаружения и распознавания объектов.
2. Проведение серий экспериментов, подтверждающих (или опровергающих) теоретические оценки границ возможного и невозможного в цифровой голографии.
3. Изучение более широкого набора технических средств цифровой голографии: графопостроители, фотолитографические устройства, управляемые от ЭВМ пространственные модуляторы устройства о управляемым лазерным лучом и т.д.
4. Анализ более широкого класса голограмм и интерферограмм.
5. Исследование реализационных аспектов цифровой голографии, связанных с затратами машинного времени на решение прямой и обратной задач.
Авторы надеятся, что выполненная имя работа привлечет внимание исследователей к решению сформулированных и постановке новых теоретических и экспериментальных задач игровой голографии.
Л и т е р а т у р а
1. Т.Хуанг. Цифровая голография. В сб.: "Применения голографии", "Мир", M., стp.65, 1973.
2. В.А.Сойфер. Цифровая голография. Достижения и проблемы. Материалы IX Всесоюзной школы по голографии и когерентной оптике. ЛИЯФ, Л., стр.199, 1977.
3. Л.П.Ярославский, Н.С.Мерзляков. Методы цифровой голографии. "Hayка", М., 1977.
4. B.R.Brown, A.W.Lohmann. Appl.Opt., 5, 6, 967, 1966.
5. М.А.Голуб, С.В.Карпеев, Е.С.Нежевенко, В.А.Сойфер, В.И.Хоцкии. Исследование пространственных фильтров, синтезированных на ЭВМ. В сб.: "Вопросы кибернетики", вып.62, М., стр.56, 1979.
6. В.А.Сойфер. "Автометрия", №3, стр.16, 1978.
7. Г.Ван Трис. Теория обнаружения, оценок и модуляции. Том 1, "Сов.радио", М., 1972.
8. Г.Ван Трис. Теория обнаружения, оценок и модуляции. Том 3, "Сов.радио", М., 1977.
9. C.H.Helstrom. J.Opt.Soc.Amer., 57, 3, 297, 1967.
10. Д.Д.Кловский, В.А.Сойфер. Обработка пространственно-временных сигналов, "Связь", М., 1976.
11. B.C.R.Ewan. Appl.Opt., 18, 5, 625, 1979.

