|
|
 |
 |

|
| |
ПРИНЦИПЫ КОРРЕЛЛЯЦИОННОЙ ФИЛЬТРАЦИИ В ГОЛОГРАФИИ
Г.Р.Локшин
Обсуждаются принцип "коррелляционной голографии", позволяющие использовать фильтрацию в Фурье-плоскости оптической системы для записи на фоторегистрирующей среде полной амплитудно-фазовой информации о волновом поле предмета без использования опорного пучка.
За последние два-три десятка лет в оптике сформировалось новое направление исследований, которое получило название радиооптика (или фурье-оптика) /1-3/. Радиооптика оперирует языком теории линейных колебательных систем (линейных фильтров), т.е. языком, который уже давно и прочно вошел в радиофизику, радио-электронику, теорию связи и другие прикладные разделы электродинамики.
На радиофизическом языке любая оптическая система рассматривается как линейный фильтр, служащий для преобразования информации, заключенной в пространственной структуре световой волны. Свойства любой линейной системы можно характеризовать функцией Грина, которую в радиотехнике - в задачах временной фильтрации - называют импульсным откликом, а в оптике - в задачах пространственной фильтрации - функцией рассеяния точки. Импульсный отклик h(t,τ) представляет собой сигнал на выходе линейного радиофильтра (в момент времени t), обусловленный δ -импульсом, появившимся на входе фильтра в момент τ. Аналогичным образом, функция рассеяния точки h(х,у,ξ,η) есть поле в выходной плоскости оптической системы, созданное точечным источником света, расположенным в точке (ξ,η) βходной плоскости. Задавая таким образом свойства линейного фильтра, мы связываем непосредственно входной и выходной сигналы интегралом суперпозиции вида:
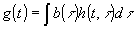 (1) (1)
(если речь идет о временных фильтрах) и
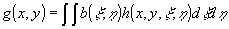 , (2) , (2)
если исследуются пространственные фильтры.
Хорошо известно, однако, что "временной" или "полевой" (если мы говорим об оптической системе) подход, основанный на равенствах (1) или (2), - не единственно возможный способ решения задач линейной фильтрации. И в радиофизике, и в фурье-оптике всегда, когда это возможно, стараются оперировать не сигналами, а их спектрами, и характеризовать свойства линейной системы не функцией Грина, а ее преобразованием Фурье - частотной характеристикой. Дело в том, что в случае, когда временной фильтр является стационарным, а оптическая система - изопланатической. функции вида е iωt или ei(ux+vg) являются собственными функциями. В этом случае удобно представлять входные сигналы в виде линейной суперпозиции собственных функций:
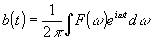 ; ; 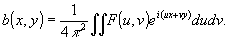 (3) (3)
Физический смысл написанных равенств понятен: первое из них есть представление входного сигнала радиофильтра в виде суперпозиции гармонических колебаний, а второе - представление комплексной амплитуды волны во входной плоскости оптической системы в виде суперпозиции плоских волн; при этом "пространственные частоты" ( u,v) есть x и у - компоненты волнового вектора плоской волны. Разложения (3) приводят к равенствам
G(ω)=F(ω)∙H(ω); G(u,v)=F(u,v)∙H(u,v), (4)
которые являются основой спектрального подхода к изучению свойств линейных систем. При таком подходе свойства системы характеризуются частотной характеристикой: Н(ω) - в задачах временной фильтрации в Н( u,v) - в задачах пространственной фильтрации.
Особенно продуктивным является спектральный подход при изучении оптических систем. Это обстоятельство тесно связано со свойством основного элемента любой оптической системы-линзы фокусировать параллельный пучок света. Каждая плоская волна, входящая в состав суперпозиции (3) и характеризуемая парой чисел
(u,v) , фокусируется линзой в свою точку фокальной плоскости. Другими словами, линза физически осуществляет спектралъное разложение Фурье, поскольку различные гармоники пространственно разделяются в этой плоскости (именно поэтому фокальную плоскость называют Фурье-плоскостью). При этим появляется возможность избирательного воздействия на отдельные спектральные компоненты; достаточно поместить в фурье-плоскость транспарант с определенной функцией пропускания, и мы получаем систему, частотная характеристика которой точно соответствует функции пропускания транспаранта. Описанный способ фильтрации - с помощью масок, установленных в фурье-плоскости - получил в оптике название корреляционная фильтрация /4/.
Методы корреляционной фильтрации в оптике уже нашли применение при решении caмыx разнообразных задач: улучшение качества оптических изображений и характеристик оптических систем, визуализация фазовых объектов, выполнение разнообразных математических операции, согласованная фильтрация и распознавание образов и т.д. Особо упомянем задачи визуализации фазовых объектов (и аналогичные им радиотехнические задачи преобразования частотно модулированных колебании в колебания, модулированные по амплитуде). Этот круг задач впервые с единых для радиотехники и оптики позиций рассмотрен в блестящей работе С.М.Рытова /5/ (радиотехнический прием "без несущей" и метод темного поля в оптике; прием с изменением фазы несущей и метод фазового контраста и т.д.). Сущность упомянутых методов состоит в таком изменении амплитудно-фазовых соотношений между гармоническими составляющими входного сигнала, которое обеспечивает преобразование фазовой модуляции в амплитудную. В настоящей работе мы проиллюстрируем возможности методов корреляционной фильтрации, обсудив фазовую проблему в более широком аспекте: мы рассмотрим задачу регистрации полной амплитудно-фазовой информации, содержащейся в световой волне, дифрагированной на произвольном (не обязательно чисто фазовом) объекте. Проблема состоит в том, что все приемники оптического излучения являются квадратичными приемниками, регистрирующими квадрат модуля комплексной амплитуды, а при та-
кой регистрации теряется, как известно, фазовая информация.
Понятно, что нельзя обсуждать возможности оптических методов обработки информации в отрыва от характеристик детектирующего устройства, поэтому оптическую систему, осуществляющую требуемый алгоритм преобразования, и последующий детектор, регистрирующий результат обработки, следует рассматривать как единый каскад (рис.1).
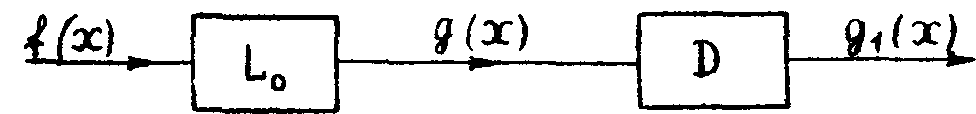
Рис.1. Блок-схема оптической системы L0 регистрирующего устройства D.
Собственно оптическая система L0 является линейным фильтром, сигнал на выходе которого g(x) связан с входным сигналом b(х) линейным преобразованием:
g(x)=L0[b(x)],
характер которого зависит от "конструкции" оптической системы, т.е. от конкретного расположения линз, транспарантов и т.д.
Фоторегистрирующее устройство является квадратичным приемником:
g1(x)=|L0[b(x)]|2, (5)
и поэтому не содержит фазовой картины результата преобразования L0.
Голография является одним из способов решения фазовой проблемы. Традиционная схема состоит в том, что на вход детектора, наряду с сигналом g(х)=L0[b(x)], прошедшем обработку в линейном фильтре L0, подается опорный когерентный фон, напри-
мер, плоская волна (рис.2). Тогда суммарный сигнал на входе детектора есть
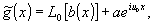 (6) (6)
а его отклик 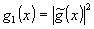 содержит, в отличие от (5), полную амплитудно-фазовую информацию, содержащуюся на выходе линейной системы L0 содержит, в отличие от (5), полную амплитудно-фазовую информацию, содержащуюся на выходе линейной системы L0
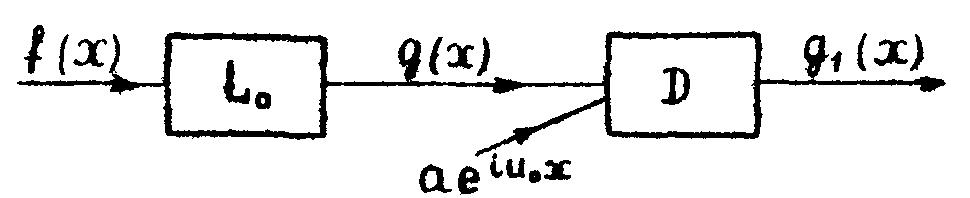
Рис.2. Голографический способ регистрации.
Известны трудности, которые присущи традиционному голографическому методу регистрации: высокие требования к временной и пространственной когерентности излучения, механической стабильности голографической установки, необходимость введения специального канала опорного луча. Поэтому ведется поиск других схем регистрации, которые не требуют независимого когерентного фона и в которых этот фон так или иначе обусловлен отражением от самого голографического объекта /6-9/.
Ясно, что в этом случае требования к механической стабильности и когерентности оказываются сильно сниженными.
Вновь обратимся к блок-схеме, изображенной на рис.1, и поставим вопрос так: можно ли, изменив определенным образом алгоритм обработки входного сигнала, т.е., введя вместо оператора L0 как-то связанный с ним оператор L, зафиксировать с помощью квадратичного детектора полную информацию об исходном преобразовании L0? Другими словами, ставится задача выделения опорного когерентного фона в процессе обработки сигнала линейной оптической системой.
Пусть нам удалось осуществить такое линейное преобразование L, в результате которого сигнал на выходе филътра имеет вид (6), т.е.:
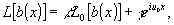 (7) (7)
где β и γ - некоторые комплексные константы. Тогда отклик детектора так же, как и при традиционном способе записи голограммы с наклонной опорной волной, будет содержать полную информации о результате преобразования L0. С точки зрения математики, различия между формулами (7) и (6) нет. Различие существует в физических способах реализации этих формул. Второе слагаемое в формуле (6) описывает независимый когерентный фон, тогда как в формуле (7) - часть сигнала, выделенную путем изменения алгоритма его обработки линейной системой L. Необходимое изменение алгоритма обработки может быть связано с введением линейного фильтра L1, установленного последовательно с L0. Таким образом, линейная система L (рис.3) представляет собой каскад, состоящий из последовательно расположенных фильтров L0 и L1.

Рис.3. Изменение алгоритма преобразования с помощью линейного фильтра L1.
Рассмотрим фильтр L1 с частотной характеристикой
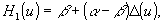
где Δ (u) - функция, отличная от нуля на достаточно малом интервале частот Δ, например, единично-нулевая функция:
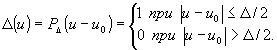
Если спектр входного сигнала и частотная характеристика фильтра L 0, осуществляющего требуемую обработку, мало меняются на интервале Δ, так что внутри интервала 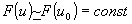 , , 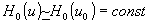 , то спектр сигнала на выходе системы L (то есть на входе квадратичного детектора) можно представить в виде , то спектр сигнала на выходе системы L (то есть на входе квадратичного детектора) можно представить в виде
G(u)=βF(u)H 0(u)+(α-β)F(u0)H 0(u 0)P 0(u-u 0).
Преобразуя обе части последнего равенства по Фурье, получаем
L[b(x)]=βL0[b(x)]+(α-β)F(u0)H 0(u 0)P Δ(u-u0). (8)
При правильном выборе интервала Δ функцию sinxΔ/x можно считать константой во всей области, где первое слагаемое в (8) отлично от нуля, и мы приходим к формуле (7), где константа γ имеет вид: γ=(α-β)F(U0)Н0(u 0)Δ,
Ясно, что соответствующим выбором констант α и β можно добиться примерного равенства интенсивностей обоих слагаемых в (8) и обеспечить тем самым высокую контрастность записанной интерференционной картины. Кроме того, при достаточно высокой частоте u0 действительное и мнимое изображения не будут создавать взаимных помех при восстановлении (в принципе частота u0 ограничена лишь полосой пропускания оптической системы L).
На рис.4 приведен пример оптической схемы, с помощью которой осуществляется весь процесс преобразования.
Сигнал, подлежащий обработке, формируется в передней фокальной плоскости линзы Л 1 (входная плоскость системы). Квадратичный детектор (фотопластинка) располагается в задней фокальной плоскости линзы Л2, (выходная плоскость). В общей фокальной плоскости линзы Л1 и Л2 (фурье-плоскость оптической системы) помещаются два транспаранта: Т0(х), задающий требуемый алгоритм обработки, и Т1(х), вносящий необходимое возмущение. Модуляционные характеристики (комплексное пропускание) транспарантов связаны с частотными характеристиками Н0(х) и Н1(х)
очевидными равенствами: 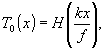 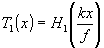 , где f -фокусное расстояние линз, , где f -фокусное расстояние линз, 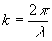 - волновое число. - волновое число.
При Т 0(х)≡1 приведенная на рис.4 схема может служить для получения голограммы объекта (находящегося на некотором расстоянии z0 от входной плоскости оптической системы). Поясним суть метода корреляционной голографии несколькими примерами.
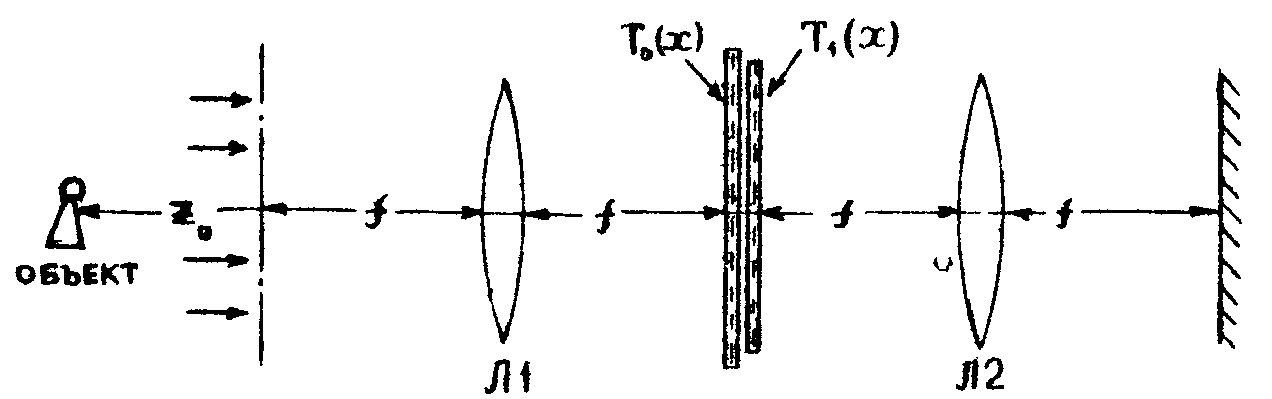
Рис.4.Оптическая схема "корреляционной голографии".
1. Метод темного поля (α=0, β=1)
H1(u)=1-P Δ(u-u0)
Маленький непрозрачный экран перекрывает точку u0 Фурье-плоскости (рис.5). Спектр изображений имеет при этом вид G(u)=F(u)-F(u0)PΔ(u-u0), а соответствующее поле на фотопластинке: g(х)=b(х)+F(u0)Δe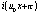 . Роль когерентного фона играет здесь отсутствующая (!) гармоника частоты u0. При u0=0 получаем аналог габоровской схемы. . Роль когерентного фона играет здесь отсутствующая (!) гармоника частоты u0. При u0=0 получаем аналог габоровской схемы.
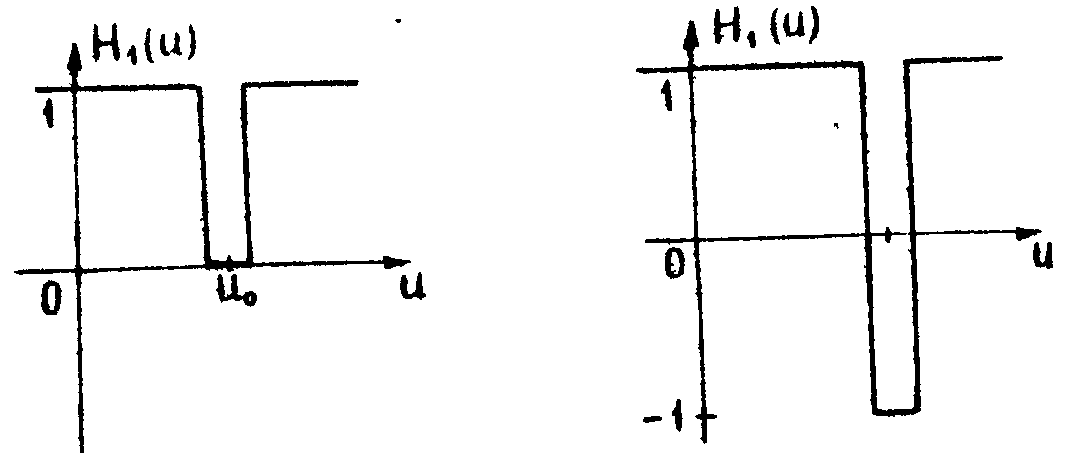
Рис.5. Метод темного поля. Рис.6. Метод фазового контраста.
2. Метод фазового контраста (α=-1, β=1)
Н 1(u)=1-2P Δ(u-u0), рис.6.
Вместо непрозрачного экрана в точке u0 Фурье-плоскости устанавливается прозрачная пластинка, вносящая фазовую задержку в π. При этом спектр выходного сигнала имеет вид:
G(u)=F(u)-2F(u0)P Δ(u-u0),
и, следовательно, поле на фотопластинке есть
g(x)=b(x)-2F(u0 )Δe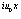 . .
Оба рассмотренных метода имеют существенный недостаток: aмплитуда слагаемого, играющего роль когерентного фона, пропорциональна частотному интервалу Δ и оказывается слишком малой, если спектр поля b(х) не содержит δ -функцию на опорной частоте u0.
3. Частично-поглощающей экран с отверстием (α=1, β=ε<1)
Ситуацию можно улучшить с помощью частотной характеристики, изображенной на рис.7: H1(u)=ε+(1-ε)πΔ(u-u0).
В этом случае получаем
g(x)=εb(x)+(1-ε)ΔF(u 0)e 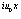 . (9)
При правильном выборе Δ и ε можно добиться примерного равенства интенcивностей двух слагаемых в (9) и обеспечить хороший контраст.
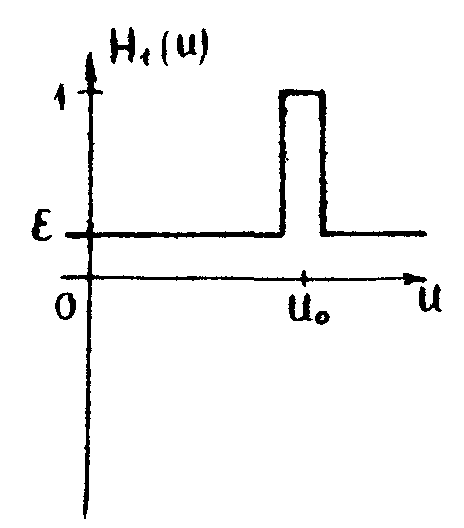
Рис.7. Поглощающий экран с отверстием с Фурье-плоскости.
4. Синтез голограммы из спектра плоских волн
Рассмотрим меняющуюся за время экспонирования частотную характеристику вида
H1(u,t)=P Δ(u-u0)+PΔ(u-at). (10)
Она реализуется с помощью непрозрачного экрана с двумя отверстиями, одно из которых, в точке u0 - неподвижно, а положение второго - в точке u(t)=at - линейно меняется в процессе экспонирования. Первое слагаемое в (10) обеспечивает постоянный когерентный фон, а второе слагаемое меняется со временем, пробегая за время экспонирования весь частотный интервал. Поле на фотопластинке в момент времени t есть
g(x,t)=F(u0 )Δe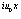 +F(at)Δe +F(at)Δe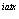 . .
Отклик детектора, пропорциональный величине 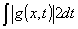 , содержит слагаемое: , содержит слагаемое:
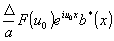
-действительное изображение и
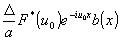 - -
мнимое изображение.
Описанный метод является аналогом метода синтеза изображения из отдельных точек предмета /10/, с той разницей, что фильтрация переносится из плоскости предмета в фурье-плоскость оптической системы. Это позволяет эффективно влиять на характеристики синтезируемого изображения, подчеркивая или, наоборот, уменьшая вклад отдельных пространственных гармоник .
5. Активный фильтр в фурье-плоскости оптической системы
( α=K>0, β=1)
Частотная характеристика такого фильтра имеет вид :
H1(u)=1+K РΔ(u-u0).
Вместо (9) получаем
g(x)=b(x)+(k-1)ΔF(u 0)e 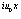 .
Для усиления интервала Δ пространственных гармоник может быть использован одномодовый резонансный усилитель. В этом случае пространственная структура усиленного поля не зависит от конфигурации входного поля /11/, поэтому тот же усилитель можно использовать для восстановления изображения.
Приведенными примерами, по-видимому, не исчерпываются возможности методов корреляционной голографии. Проблема может быть решена и с помощью частотных характеристик другого вида, быть может с использованием методов фильтрации на стадии восстановления голограмм.
Л и т е р а т у р а
1. В.А.Зверев "Радиооптика", М., Сов. Радио, стр. 138-186, 1975.
2. Дж.Гудмен. "Введение в фурье-оптику", М., "Мир", стр.136-215, 1970.
3. А.Папулис. "Теория систем и преобразований в оптике", М., Мир, 1971.
4. Дж.Строук. Введение в когерентную оптику и голографию. М., "Мир"; стр.15-29, 1967.
5. С.М.Pытов. O методе фазового контраста в микроскопии,УФН, 41, стр.425, 1950.
6. Л.В.Ковальский, В.К.Полянский. Оптика и спектроскопия, 28, №2, стр.336-341, 1970.
7. Г.В.Скроцкий, И.С.Клименко, УФН, 109, №2, 1970.
8. O.Bryngdahl, A.W.Lohman. Journ.Opt.Soc.Am., 60, 281, 1970.
9. E.Archold, A.E.Ennos. Optica Acta, 19, 4, 253, 1972.
10. Л.М.Сороко. Введение в когерентную оптику и голографию. М., ''Наука", стр.417-420, 1971.
11. С.М.Козел, Г.Р.Локшин. Радиотехника и элекроника, 20, №8, стр.1667, 1975.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

