|
|
 |
 |

|
| |
РЕГИСТРАЦИЯ И ОБРАБОТКА МОДУЛИРОВАННЫХ ОПТИЧЕСКИХ СИГНАЛОВ
В.А.Зубов, А.В.Крайский
Использование нестационарной опорной волны с линейным изменением частоты по сечению позволяет реализовать полную запись и обработку модулированного оптического сигнала. Эти вопросы были теоретически рассмотрены для монохроматического излучения в работах /1,2/. В данной работе рассматриваются эксперименты по регистрации такого сигнала, анализируется работа схем, позволяющих получить структуру сигнала и его спектр с разрешением, значительно превосходящим ширину спектра лазера и достигающим долей гц.
Схема двухканальной экспериментальной установки приведена на рис.1. Излучение лазера после диафрагмы Д1, ограничивающей однородный участок волны, делится на две части с помощью призмы ПР. В одном канале, образованном диафрагмами Д2 и Д3 и телескопической системой Л1, Л2, при квазилинейном движении составляющей Л1 формируется нестационарная волна, имеющая в плоскости регистрации вид /3/:
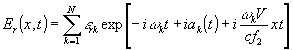 , (1) , (1)
где k - номер определенной моды излучения, полное число мод N, εrk - амплитуда, ωk - средняя частота, ak(t) - случайная фаза стой моды. Второй канал, образованный телескопической системой Л3, Д4 и зеркалом З, является рабочим. В средней фокальной плоскости этой телескопической системы осуществляется модуляция сигнала. В экспериментальной схеме воздействие объекта модулируется диском-прерывателем М. Часть излучения рабочего канала отводится полупрозрачной пластинкой на фотоприемник ФЭУ и далее регистрируется на осциллографе ОСЦ с тем, чтобы иметь информацию об амплитудной модуляции регистрируемого сигнала.
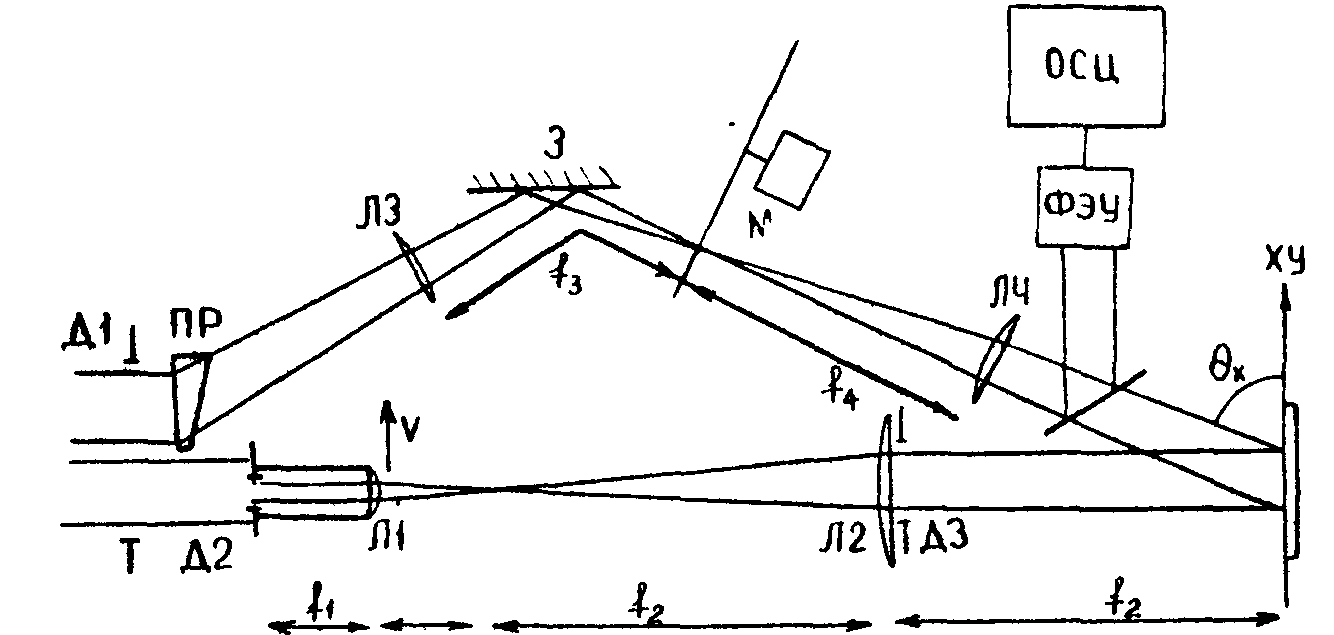
Рис.1. Схема экспериментальной установки для регистрации модулированных оптических сигналов.
Излучение из рабочего канала попадает в плоскость регистрации ху, направление распространения описывается косинусом cosθхs. Поле от объекта имеет вид:
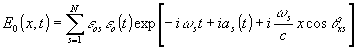 , (2) , (2)
где s - номер отдельной моды излучения лазера, ε0(t) - комплексная амплитуда, описывающая модуляцию сигнала. При выполнении обычных условий получается голограмма с амплитудной прозрачностью, содержащей две компоненты: компоненту, связанную с постоянной засветкой из двух каналов, и компоненту с информацией о сигнале. Такая голограмма может экспонироваться в течение ограниченного времени Т, поскольку оптическая система Л1, Л2 при формировании опорной волны должна работать в параксиальном приближении. В результате усреднения информации за время регистрации ненулевой вклад дают только члены с s=k. В результате имеем:
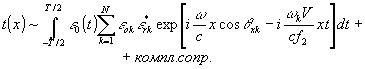 (3) (3)
При восстановлении голограмма Г освещается плоской волной. лазерного излучения (рис.2), состоящего из М мод, среднее направление распространения задается косинусом - cosθxm
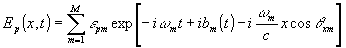 , (4) , (4)
где m - номер моды. Все расчеты выполняются в приближении Френеля.
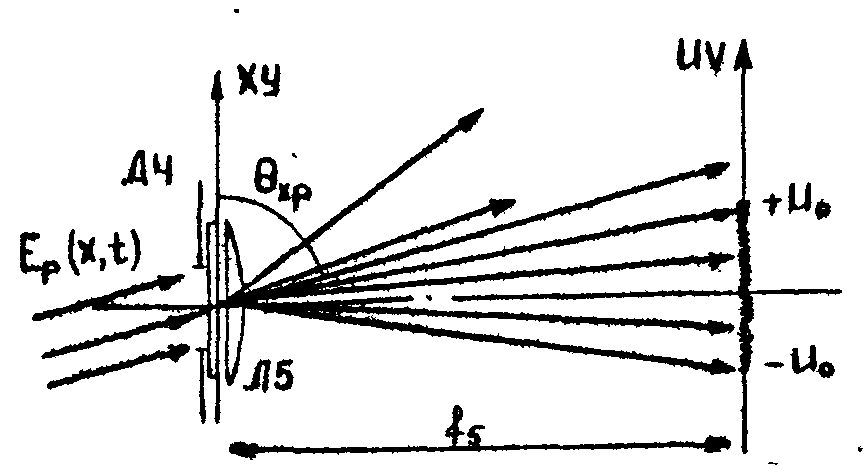
Ри c.2. Cхема воcстановления структуры модулированного сигнала.
Оптическая система Л5 выполняет на этапе восстановления операции преобразования Фурье. Примем во внимание, что 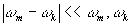 и направляющие косинусы могут быть выбраны так, что и направляющие косинусы могут быть выбраны так, что 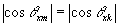 , тогда для голограммы с размером по оси х, равным 2х0 аппаратная функция имеет простой вид: , тогда для голограммы с размером по оси х, равным 2х0 аппаратная функция имеет простой вид:
 . (5) . (5)
С учетом конечного разрешения компонента поля, дающая в задней фокальной плоскости uv оптической системы картину зарегистрированного сигнала, будет
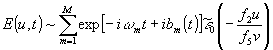 , (6) , (6)
т.е. восстанавливаются записанное модулированное поле в пространственном представлений. Разрешение будем определять расстоянием между нулями аппаратной функции (5), что дает
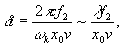  . (7) . (7)
Положение восстановленного изображения задается максимумом аппаратной функции для моментов времени t=±T/2, его размер и число разрешаемых элементов равны
 , , 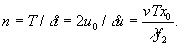 (8) (8)
Эксперимент выполнялся при следующих значениях величин:
λ=0,63∙10 -3 мм, Т=6,8 с, v~2 мм/с, f2=300 мм, f5=300 мм, 2x0~8 мм. Расчет дает: |cosθkr|≤0,023, 2U 0≤ 14 мм, δt~25 мc, δu~0,05 мм, n~280.
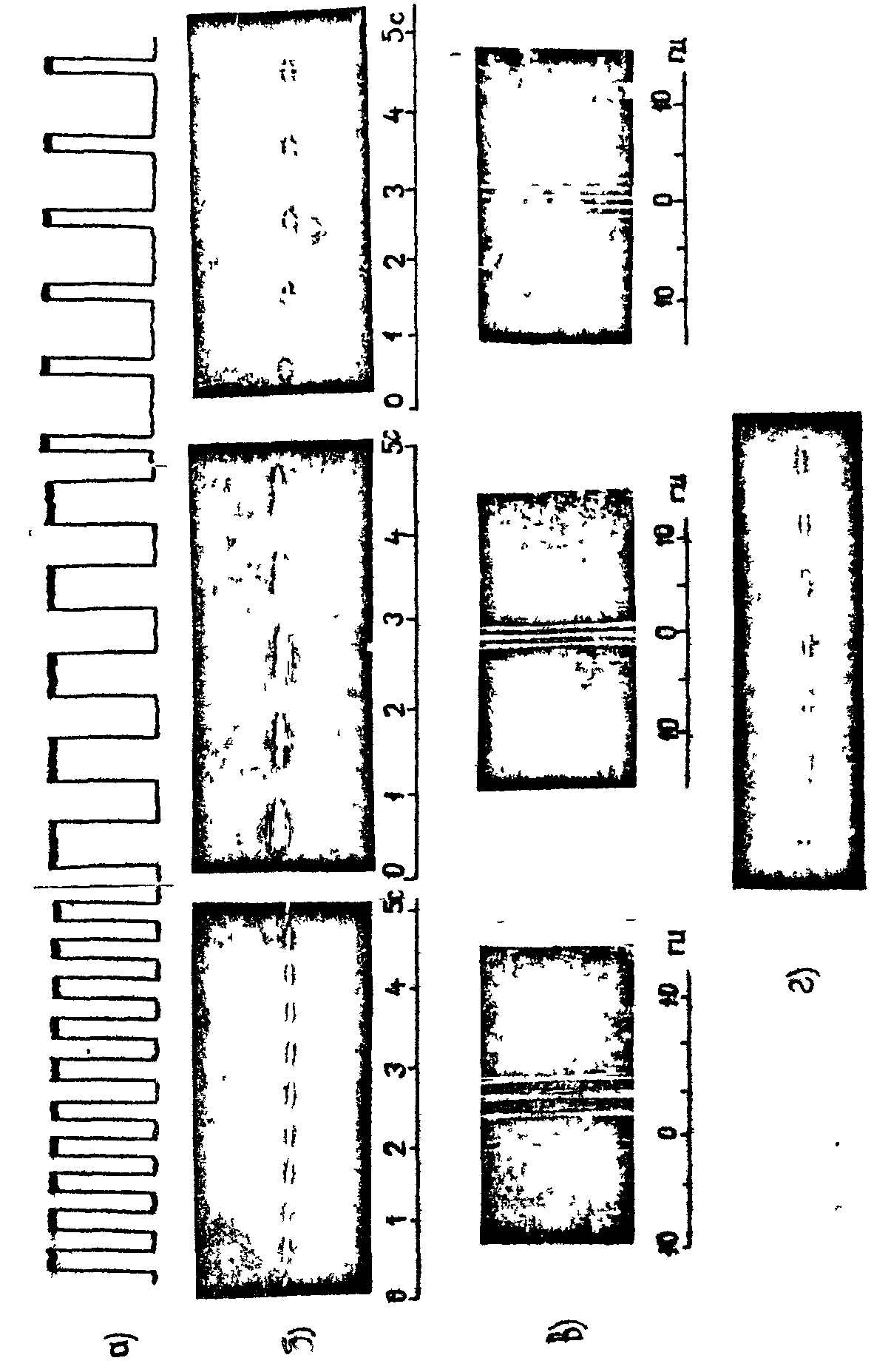
Результаты эксперимента для различных частот модуляции и различных скважностей представлены на рис.3.
Схема получения спектра модулированного сигнала F(Ω) с использованием стационарной восстанавливающей волны (4) представлена на рис.4. Поле в плоскости наблюдения ХY, оптически сопряженной с голограммой Г, на основании (3) в рамках условий, использовавшихся при выводе (5), имеет вид:
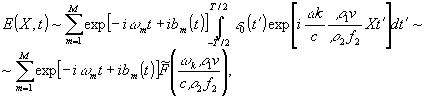 (9) (9)
где знак "Тильда" соответствует свертке спектра сигнала с аппаратной функцией. Для пространственного разрешения в плоскости регистрации на основании (9) в (8) получаем:
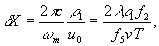 (10) (10)
Для оценки спектрального разрешения воспользуемся представлением ε 0(t) в виде фурье-образа F(Ω), что дает аппаратурную функцию
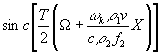 . (11) . (11)
Оценка ширины аппаратной функции выполняется подобно (7) и дает δ Ω=4π/T. Следует отметить, что с точки зрения спектрального разрешения более правильно исходить из критерия Релея, т.е. δΩp=δΩ/2=2π/, или, переходя от круговых частот к обычным,
δν р=I/T и δXp=λρ2f 2/ρ1vT. (12)
Таким образом, спектральное разрешение определяется полным временем регистрации. Область дисперсии определяется диапазоном частот, зарегистрированным на голограмме, который равен
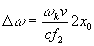 или 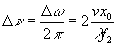 . (13) . (13)
Дисперсия в плоскости регистрации (см.(12)) и число разрешаемых элементов (см.(13)и (12)) равны
δνр/δXp=vρ1/λρ2f 2, n=Δν/δνp=2 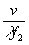 x 0T. (14)
Линейный размер спектра определяется максимумом аппаратной функции для пространственного разрешения при х =±x0, что дает
2X0=2x0 ρ2/ρ1. (15)
С учетом величин, которые использовались на эксперименте (ρ 1 = 125 мм, ρ2 = 260 мм, f5 = 85 мм), получаем следующие оценки: δΩ~0,9 c -1, δνp~0,15 гц, δXp~0,03 мм, Δν~85 гц, δνp/δXp~5 гц/мм, 2Х0~16,5 мм, n~550.
Результаты эксперимента представлены на рис.3. Как отмечалось, воздействие объекта на сигнал моделировалось модуляцией с частотами 1,03 и 2,06 гц с разными скважностями. Расчет частот модуляции по спектрограммам дает 1,0 и 2,0 гц. Иллюстрации показывают, что реальное разрешение значительно превосходит 1 гц.
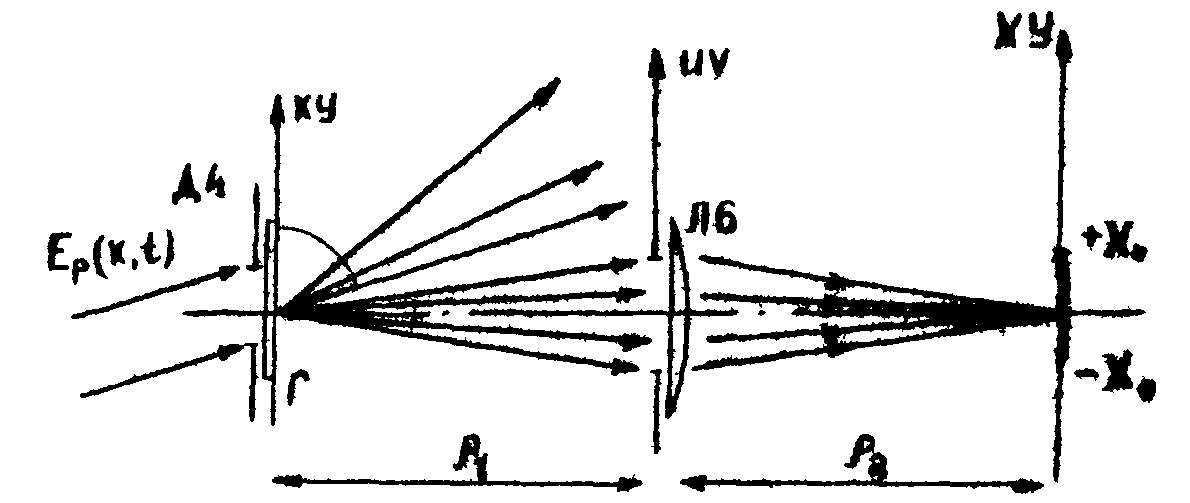
Рис.4. Схема получения спектра модулированного оптического сигнала.
Л и т е р а т у р а
1. В.А.Зубов, А.В.Крайский, Т.И.Кузнецова. Письма ЖЭТФ, 13, 443, 1971.
2. В.А.Зубов. Краткие сообщения по физике, № 7, 17, 1972.
3. В.Н.Боркова, В.А.Зубов. Материалы семинара "Новые разработки в области оптической голографии и их промышленное использование", стр. 21, Изд. ЛДНТП, Ленинград, 1979.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

