СТРУКТУРА И КАЧЕСТВО ГОЛОГРАФИЧЕСКОГО ПРОЦЕССА В.Б.Немтинов
Исследованы основные дифракционно-голограммные типа, обусловленные структурой дифракционных порядков на стадии восстановления. Введено понятие принципиальной оптико-голографической схемы и приведены примеры схем. Показано, что понятие типа голограммы лежит в основе структурного подхода к оценке качества голографического процесса.
Введение
В строгой постановке задача структурного анализа голографического цикла опирается на теоретико-групповую структурную модель (СМ) обобщенного голографического процесса (ОГП), лежащую в основе структурной теории голографии (СТГ). Она позволяет ввести строгое понятие обобщенного типа голограммы (ОТГ) как типа симметрии ОГП 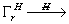
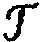
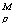 в виде отображения
в виде отображения 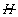 , дифракционно-голографического типа
, дифракционно-голографического типа 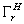 в дифракционно-голограммный тип
в дифракционно-голограммный тип 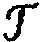
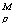 . Голографический оператор описывает действие регистрирующей среды и связывает групповые структуры голографического и голограммного полей. Иначе говоря, ОТГ складывается из:1) голографического подтипа
. Голографический оператор описывает действие регистрирующей среды и связывает групповые структуры голографического и голограммного полей. Иначе говоря, ОТГ складывается из:1) голографического подтипа 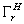 = r + Н, определяемого преобразованным голографическим полем, где r=arexp(iφr) - опорная волна, Н- подгруппа предметных волн h=ahexp(iφh); 2) регистрационного подтипа
= r + Н, определяемого преобразованным голографическим полем, где r=arexp(iφr) - опорная волна, Н- подгруппа предметных волн h=ahexp(iφh); 2) регистрационного подтипа 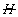 . определяемого преобразующими свойствами среды, носителя и дополнительной обработкой; 3) голограммного подтипа
. определяемого преобразующими свойствами среды, носителя и дополнительной обработкой; 3) голограммного подтипа 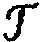
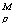 =ρΜ, определяемого голограммным преобразованным полем, где ρ - классификационный элемент, М - подгруппа голограммных образов.
=ρΜ, определяемого голограммным преобразованным полем, где ρ - классификационный элемент, М - подгруппа голограммных образов.
Все колличественные характеристики качества голографического процесса сводятся к анализу структуры и числа дифракционных порядков (ДП). Понятие ДП как совокупности плоских волн, соответствующей определенному участку пространственно-частотного спектра восстановленной волны и распространяющейся в определен-
ном направлении, играет важную роль в структурном анализе ГП. Максимум в спектре ДП характеризует среднее направление распространения волнового фронта (направление восстановленного ДП). Поэтому для выделения полной информации о главном W2А, сопряженном Wсп и неотклоненном W0 изображениях используется матричный амплитудный коэффициент пропускания А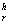 /1,2/.
/1,2/.
Структурный анализ ОГП и понятие ОТГ являются отправным моментом при введении принципиальных обозначений*) элементарных структурных блоков для описания голографических схем /1,2/. В настоящее время все схемы записи в восстановления голограмм (да и оптические схемы тоже) являются по своему содержанию монтажными схемами. При этом, с одной стороны, в каждой монтажной оптико-голографической схеме имеется большое количество лишних, несущественных деталей, а с другой стороны, отсутствуют главные структурные элементы типа сигналов и характера преобразования. Именно понимание и правильное использование групповой структуры ОГП позволяет от монтажных схем перейти к принципиальным, которые отражают основное структурно-физическое содержание голограммы.
1. Дифракционно-голограммная классификационная категория
В работах /1,2/ исследована дифракционно-голографическая классификационная категория Кг, состоящая из совокупности пар {ГrH, МrH} дифракционно-голографических типов ГrH и их матричных голограммных образов МrH, и построены основный элементарные дифракционно-голографические типы. Модулирующие свойства регистрирующей среды обуславливают амплитудно-фазовую классификацию регистрационных типов /2/. Дифракционно-голограммная классификационная категория завершает структурную классификацию голограмм. Ее элементы должны описывать реконструирующие свойства голограммной подгруппы МrH. Структурное выделение новых, интенсивно
развивающихся направлений, таких как динамическая голография /3/ или метод обращения волнового фронта /4/, связано с построением моделей нелинейной регистрирующей среды (регистрационного подтипа 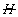 ).
).
В /1/ рассмотрены основы феноменологической структурной теории процесса реконструкции голограмм, опирающейся на матричное Представление 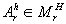 амплитудного коэффициента пропускают плоской голограммы. Причем для голограмм Денисюка Аrh играет роль амплитудного коэффициента отражения. Матричная запись обладает большим числом степеней свободы, чем запись в виде амплитудного коэффициента пропускания, выражает симметрию процесса восстановления и позволяет разделить процесс реконструкции главного, сопряженного и неотклоненного изображения. В основе замены голограммы реконструирующим оператором R(Аrh) лежит идея представления голограммы в виде элементарной системы с распределенными параметрами или элементарного распределенного голограммного блока /1,2/. В распределенных системах понятие элементарного блока обычно связывается с математической или физической моделью хорошо изученного физического процесса. В случае тонких голограмм таким процессом является процесс восстановления идеальной двумерной голограммы, описываемой с помощью амплитудного коэффициента пропускания. При этом на выражение
амплитудного коэффициента пропускают плоской голограммы. Причем для голограмм Денисюка Аrh играет роль амплитудного коэффициента отражения. Матричная запись обладает большим числом степеней свободы, чем запись в виде амплитудного коэффициента пропускания, выражает симметрию процесса восстановления и позволяет разделить процесс реконструкции главного, сопряженного и неотклоненного изображения. В основе замены голограммы реконструирующим оператором R(Аrh) лежит идея представления голограммы в виде элементарной системы с распределенными параметрами или элементарного распределенного голограммного блока /1,2/. В распределенных системах понятие элементарного блока обычно связывается с математической или физической моделью хорошо изученного физического процесса. В случае тонких голограмм таким процессом является процесс восстановления идеальной двумерной голограммы, описываемой с помощью амплитудного коэффициента пропускания. При этом на выражение
W=W0+W2A+Wсп (1)
можно смотреть как на разложение восстановленной волны W по системе из трех ДП, задаваемых матрицей Аrh.
Отправным моментом структурной теории процесса восстановления является понятие дифракционной конфигурации (ДК), под которой понимается любая комбинация преобразованных ДП на выходе голограммы. Так как возникновение ДП связано как с дифракционным рассеянием, так я брэгговским отражением, то определенные совокупности восстановленных ДП играют различную роль. К введению ДК приводит анализ влияния толщины регистрирующей среды и нелинейных искажений ДП, который требует учитывать специфику взаимодействия восстанавливающих волн с различными компонентами ампли-
тудного пропускания (матричными элементами матрицы Аrh). Впервые структура ДП рассмотрена в рампах кинематической теории процесса реконструкции объемных голограмм /5/. В первом борновском приближении, пренебрегая затуханием восстанавливающей волны при прохождении ее через голограмму, а также вторичным взаимодействием восстановленной волны со структурой голограммы в /5/, доказана основная роль отраженного главного (брэгговского) ДП в формировании восстановленного изображения.
Современное состояние теории трехмерных голограмм рассмотрено а /6/. Дальнейшим развитием кинематической теории явилась теория связанных волн /7/, которая учитывает, что восстановленная волна прежде чем покинуть объем голограммы взаимодействует с ее структурой. При этом на первоначальные падающую и восстановленную волны накладываются вторичные волны, совпадающие с ними по направлению, но отличающиеся по фазе. Хотя теорию связанных волн нельзя рассматривать как теорию объемной голограммы во втором приближения, но на ее основе можно в первом приближении строго задать структуру ДП. В самом деле, в рамках теории связанных волн поле W на выходе голограммы при идеальной реконструкции представляет собой сумму брэгговской дифрагированной (отраженной) волны W11 и прошедшей (падающей) частично дифрагированной волны W12. Со структурной точки зрения каждая из волн W11 и W12, получающаяся из восстанавливающей волны V, представляет собой некоторую ДК. Эти две ДК выражают физику разделения ДП - наличие неискаженного восстановленного изображения в одной из совокупностей ДП. Например, при восстановлении тонкой пропускающей голограммой неискаженного главного изображения они имеют вид: W11=W2A, W12=W0 + Wсп. При отступлении процесса реконструкции от идеального брэгговская компонента отсутствует.
В рамках СТГ построено описание процесса восстановления голограммы как представление аддитивной матричной группы в группу реконструирующих операторов GR /1,2/. При этом совокупность двух восстановленных ДК (W11,W12) определяет комбинации ДП, в которые реконструирующий оператор R(A) переводит восстанав-
ливающую волну V. На структурном языке это означает, что восстановленная волна W равна сумме координат двумерного конфигурационного вектора (W11, W12). В свою очередь выделение ДК связано с введением реконструкционного вектора V(С11,С12), координаты которого показывают как ДП (матричные элементы матрицы Аrh) разделяются на ДК, т.е. с каким весом они входят в ДК. В случае идеальной двумерной пропускающей голограммы С11=С12=1, т.к. ДП равноправны.
Матричная запись амплитудного пропускания задает в линейном приближении структуру реконструируемой волны из трех основных ДП (структура в большом). При этом треугольный вид матрицы Аrh подчеркивает, что один из ДП является или близок к брэгговскому (столбец (r0*h) или строка (0, r, h*)) a два других ДП имеют обычную дифракционную природу (соответственно столбец 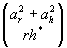 или строка (r*h, аr2+аh2). Для анализа тонкой структуры ДП (структура в малом) требуется уточнение построенной модели элементарного распределенного голограммного блока, которое может быть сделано, например, в рамках медовой теории объемных голограмм /8,9/. К тонкой структуре ДП относятся также такие явления как коррекция волнового фронта методами динамической голографии /3/ и метод обращения волнового фронта /4/.
или строка (r*h, аr2+аh2). Для анализа тонкой структуры ДП (структура в малом) требуется уточнение построенной модели элементарного распределенного голограммного блока, которое может быть сделано, например, в рамках медовой теории объемных голограмм /8,9/. К тонкой структуре ДП относятся также такие явления как коррекция волнового фронта методами динамической голографии /3/ и метод обращения волнового фронта /4/.
Матричное представление процесса реконструкции позволяет структурно отличать друг от друга случаи, когда восстанавливающая волна V падает соответственно слева или справа на голограмму. В первом случае будем говорить о сопряженном линейном пространстве восстанавливающих векторов-строк С1=(С11,С12). При этом голограммная матрица Аrh умножается на реконструкционный вектор С1 слева. Во втором случае имеется основное линейное пространство векторов-столбцов С1'=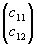 , так что голограммная матрица Аrh умножается на реконструкционный вектор С1' справа. Таким образом,
, так что голограммная матрица Аrh умножается на реконструкционный вектор С1' справа. Таким образом,
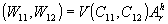 или
или 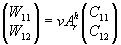 . (2)
. (2)
Структурный подход дает возможность выделить также процесс реконструкции восстанавливающей волной с комплексно-сопряженной амплитудой. Переход к комплексно-сопряженной волне соответству-
ет некоторому преобразованию симметрии: плоская волна заменяется волной, симметричной относительно нормали к голограмме; сферическая расходящаяся волна - сходящейся и наоборот. Со структурной течки зрения это преобразование симметрии соответствует переходу к транспонированной голограммной матрице
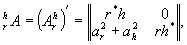 (3)
(3)
которая отражает изменение роли ДП в ДК при восстановлении комплексно-сопряженной волной.
Идеальная двумерная модель тонкой голограммы на самом деле обычно не реализуется. Реальная голограмма обладает некоторой толщиной. Если считать, что толщина регистрирующей среда не превышает размера области геометрической тени, то распределение поля в плоскости голограммы не меняется при его распространении вдоль оси z. Пусть опорная и предметная волны проходят с малым поглощением через фотослой. Тогда их комплексные амплитуды имеют вид
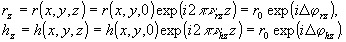 (4)
(4)
Поэтому в первом приближении матричный амплитудный коэффициент пропускания описывает объемные реконструирующие свойства реальной тонкой голограммы с помощью геометрооптического фазового сдвига
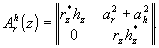 (5)
(5)
Именно фазовый множитель ехр(iΔφhz) позволяет судить о наличии или отсутствии искажений в восстанавливаемой ДК.
Структурный анализ выделяет три основные разновидности голограмм, полученных в сопутствующих или ненаправленных волнах νhrνrz>0 (коголограммы), во встречных или контрнаправленных волнах νhrνrz<0 (контрголограммы) и с использованием поверх-
ностных волн νhrνrz=0 (поверхностная голограмма). В зависимости от толщины регистрирующей среды коголограммы могут оказаться по своим параметрам близкими к объемным, а контрголограммы проявлять свойства тонких голограмм. Основной структурной характеристикой контрнаправленности является использование комплексно-сопряженной опорной волны r* в матрице амплитудного пропускания (или отражения) контрголограммы 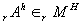 . Фактическое структурное различие тонкой и объемной голограммы состоит в том, что тонкая голограмма восстанавливает преимущественно три дифракционных порядка, а объемная голограмма восстанавливает преимущественно два дифракционных порядка (коголограмма) или один дифракционный порядок (контрголограмма). В поверхностных голограммах rz или hz заменяются на r0, h0.
. Фактическое структурное различие тонкой и объемной голограммы состоит в том, что тонкая голограмма восстанавливает преимущественно три дифракционных порядка, а объемная голограмма восстанавливает преимущественно два дифракционных порядка (коголограмма) или один дифракционный порядок (контрголограмма). В поверхностных голограммах rz или hz заменяются на r0, h0.
В общем случае голограмма обладает свойствами плоской и объемной решеток и восстанавливает дополнительные изображения в проходящем и отраженном свете. В /10/ экспериментально подтверждено, что коголограмма и контрголограмма реконструируют шесть ДП (три прошедших и три отраженных), и дано геометрооптическое обоснование этого факта. Свойство тонких пропускающих контрголограмм толщиной 0,1÷0,25 мкм исследованы в /11/. Показано, что в силу эквивалентности тонких коголограмм и контрголограмм независимо от схемы регистрации восстанавливаются прошедшее и отраженное изображения.
Так как в приближении геометрической тени влияние толщины регистрирующей среды приводит только к фазовым искажениям, то матричное представление процесса реконструкции не различает прошедшей и отраженной волны. Иначе говоря, пропускание и отражение ДП в матричной форме записи одинаково равноправны. Эта симметрия процесса восстановления приводит к тому, что со структурной точки зрения реконструируемые ДК могут относиться как к прошедшей, так и отраженной волне. В этом случае весовые коэффициенты в формуле (2) (координаты реконструкционного вектора) отличны от нуля и имеют различные значения для прошедших ДК (с11, с12) и отраженных ДК (с21, с22). В итоге, вводя в рассмотрение реконструкционную матрицу ||cmn||, получим мат-
ричный аналог (2)
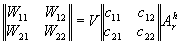 или
или 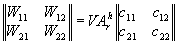 , (6)
, (6)
где строки матрицы реконструированных да ||Wkl|| описывают прошедшие (W11, W12) и отраженные (W21,W22) ДК, т.e. координаты прошедшего и отраженного конфигурационного вектора W1 и W2. Матричное представление процесса реконструкции показывает, что в линейном приближении в общем случае всегда восстанавливается шесть изображений (два конфигурационных вектора или четыре ДК); три в проходящем и три в отраженном свете. В общем случае значения матричных элементов cmn(d) зависят от толщины голограммы d и определяются, исходя из анализа тонкой структуры ДП, или находятся экспериментально. Таким образом, исследованы основные дифракционно-голограммные типы: пропускающие, отражательные, тонкие, объемные коголограммы, контрголограммы и поверхностные голограммы, восстанавливающие как главное так и сопряженное изображения. Полученные результаты сведены в табл.1.
2. Принципиальные оптико-голографические схемы
Структурная модель оптико-голографического звена (СМ ОГЗ), построенная в /2/, описывает связь между голографическим и голограммным подтипами в элементарном структурном блоке, которую устанавливает регистрирующая среда. Поэтому для построения принципиальных схем необходимо условиться об обозначениях, учитывающих специфику модулирующих свойств регистрирующей среды. На рис.1 приведены принципиальные обозначения элементарных структурных оптико-голографических блоков, описывающих только преобразующие свойства регистрирующей среды (PC): -а) тонкая PC с амплитудной модуляцией; б) тонкая РС с фазовой модуляцией; в) тонкая PC с амплитудно-фазовой модуляцией; г) объемная РС с фазовой модуляцией; е) амплитудно-модулирующая объемная PC с тонким амплитудным рельефом, ж) амплитудно-модулирующая объемная PC с тонким фазовым рельефом ; З) фазо-мо-
Таблица 1
|
Дифракционно-голограммный тип
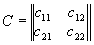
|
Пропускающий тип (с11, с12) |
|
(0,0)
Отражательный
(О) |
(1,1)
Пропускающий тонкий (ПТ) |
(1,0)
Пропускающий объемный главный (ПОГ) |
(0,1)
Пропускающий объемный сопряж.
(ПОС) |
|
Отражательныый тип (с21, с22) |
(0,0)
Пропускающий
(П) |
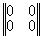
Нулевой тип ( ) |
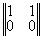
(ПТ) |
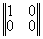
(ПОГ) |
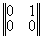
(ПОС) |
|
(1,1)
Отражательный тонкий
(ОТ) |
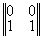
(ОТ) |
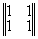
(ПТ; ОТ) |
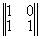
(ПОГ, ОТ) |
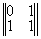
(ПОС, ОТ) |
|
(1,0)
Отражательный объемный главный (ООГ) |
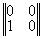
(ООГ) |
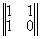
(ПТ; ООГ)
не реализуем |
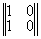
(ПОГ, ООГ) |
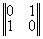
(ПОС, ООГ) |
|
(0,1)
Отражательный объемный сопряженный
(ООС) |
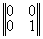
(ООС) |
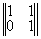
(ПТ; ООС)
не реализуем |
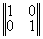
(ПОГ, ООС) |
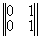
(ПОС, ООС) |
дулирующая объемная PC с тонким амплитудным рельефом. И) фазо-модулирующая объемная PC с тонким фазовым рельефом; К) объемная PC с амплитудно-фазовой модуляцией.
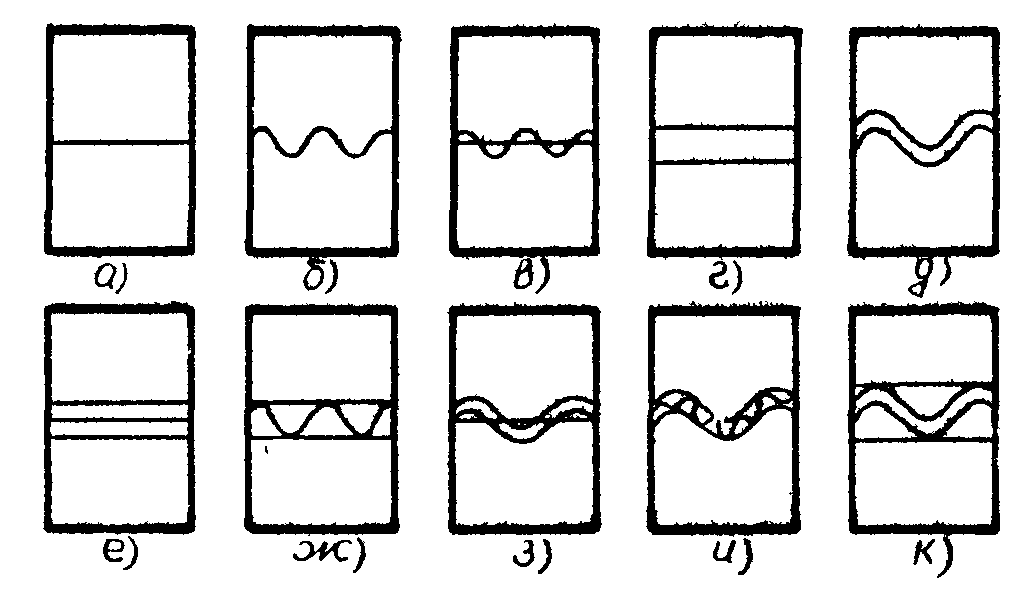
Рис.1.
В /2/ показано, что СМ можно построить для любого преобразующего устройства при условии замены голографического оператора 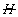 преобразующим оператором ρ. Например, можно говорить о преобразующих свойствах таких элементарных структурных блоков как слой пространства, объектив, пространственно-частотный или амплитудный фильтр, оптико-электронное преобразующее устройство и т.п. Принципиальные обозначения таких блоков должны описывать действие соответствующих преобразующих операторов. На рис.2 приведены примеры принципиальных обозначений некоторых элементарных структурных оптических преобразующих блоков, задающих только характер преобразования без учета типа входных и выходных сигналов:
преобразующим оператором ρ. Например, можно говорить о преобразующих свойствах таких элементарных структурных блоков как слой пространства, объектив, пространственно-частотный или амплитудный фильтр, оптико-электронное преобразующее устройство и т.п. Принципиальные обозначения таких блоков должны описывать действие соответствующих преобразующих операторов. На рис.2 приведены примеры принципиальных обозначений некоторых элементарных структурных оптических преобразующих блоков, задающих только характер преобразования без учета типа входных и выходных сигналов:
а) слой пространства (СП) геометрической тени, б) СП Френеля (свертка с функцией Френеля), в) СП Фраунгофера; г) СП Фурье; д) объектив, мультипликативные модулирующие свойства которого задаются аберрационной функцией зрачка /2/; е) тонкий амплитуд-
ный фильтр, ж) тонкий разовый фильтр, з) диффузный рассеивателъ.
Выделение голографических и голограммных подтипов и задание преобразующих свойств регистрирующей среды позволяет перейти к построению принципиальных оптико-голографических схем. Некоторые примеры схем даны в /1,2/. Принципиальные обозначения должны задавать тип входного сигнала, преобразующие свойства структурного блока и характер преобразования.
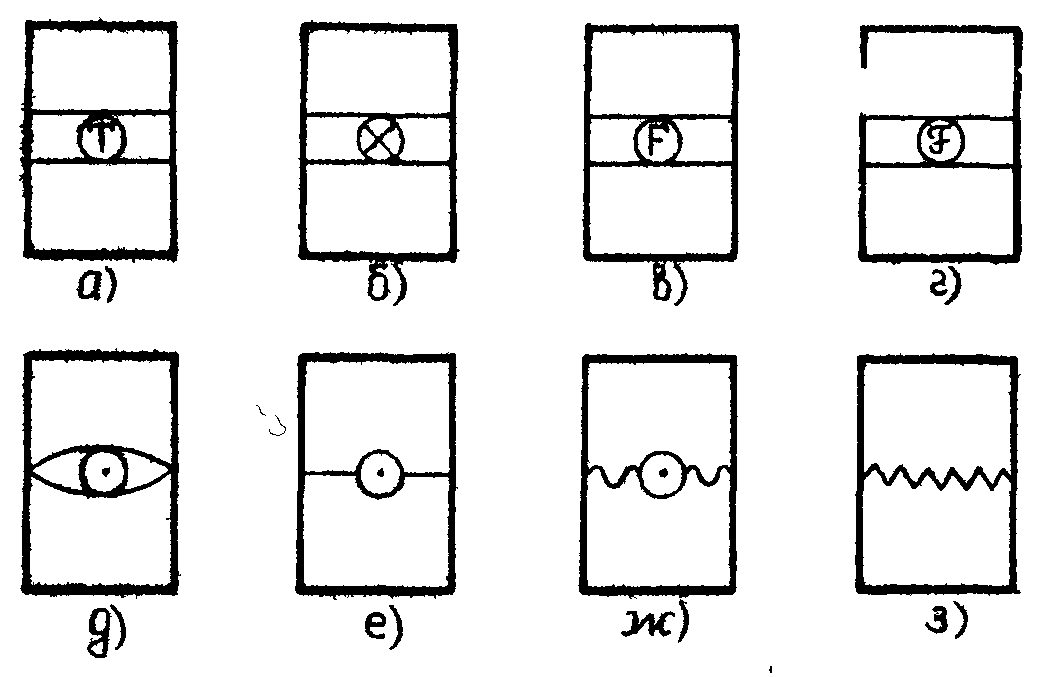
Рис.2.
На рис.3 приведена оптическая схема записи голограммы сфокусированного изображения (ГСИ) с плоской опорной волной rp в тонкой PC с фазовой модуляцией. Объектив Об формирует изображение И предмета П, которое регистрируется на голограмме Г. Принципиальная схема получения ГСИ доказана на рис.3, где 1 - композиционный оптический структурный блок (СП-Об-СП); 2 - ГСИ. Входной сигнал задается матрицей ДП, а выходной сигнал формируется в виде свертки с функцией рассеяния hоб. Результирующим расширением групповой структуры дифракционного ноля является подгруппа Hf сфокусированных образов.
На рис.4а,в даны оптические схемы записи в восстановления радужной голограммы со сферическое сходящейся опорной волной rs /12/. Предметная волна h, регистрируемая на радужной го-
лограмме Г2, формируется с помощью вспомогательной голограммы Г1, которая восстанавливает действительное изображение с помощью щелевой диафрагмы Д (рис.4а).
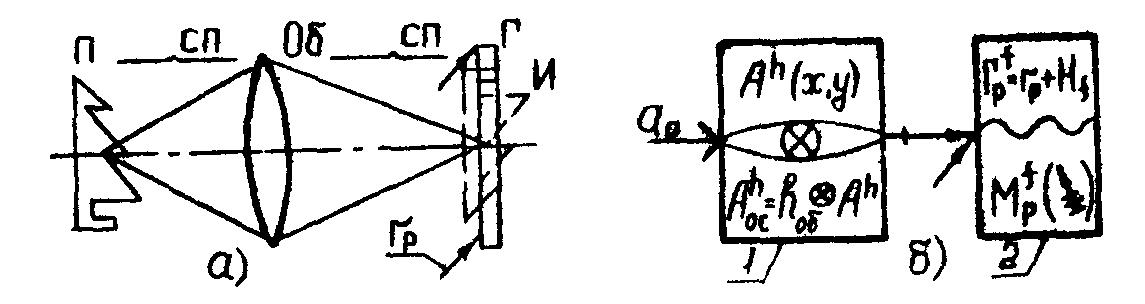
Рис.3.
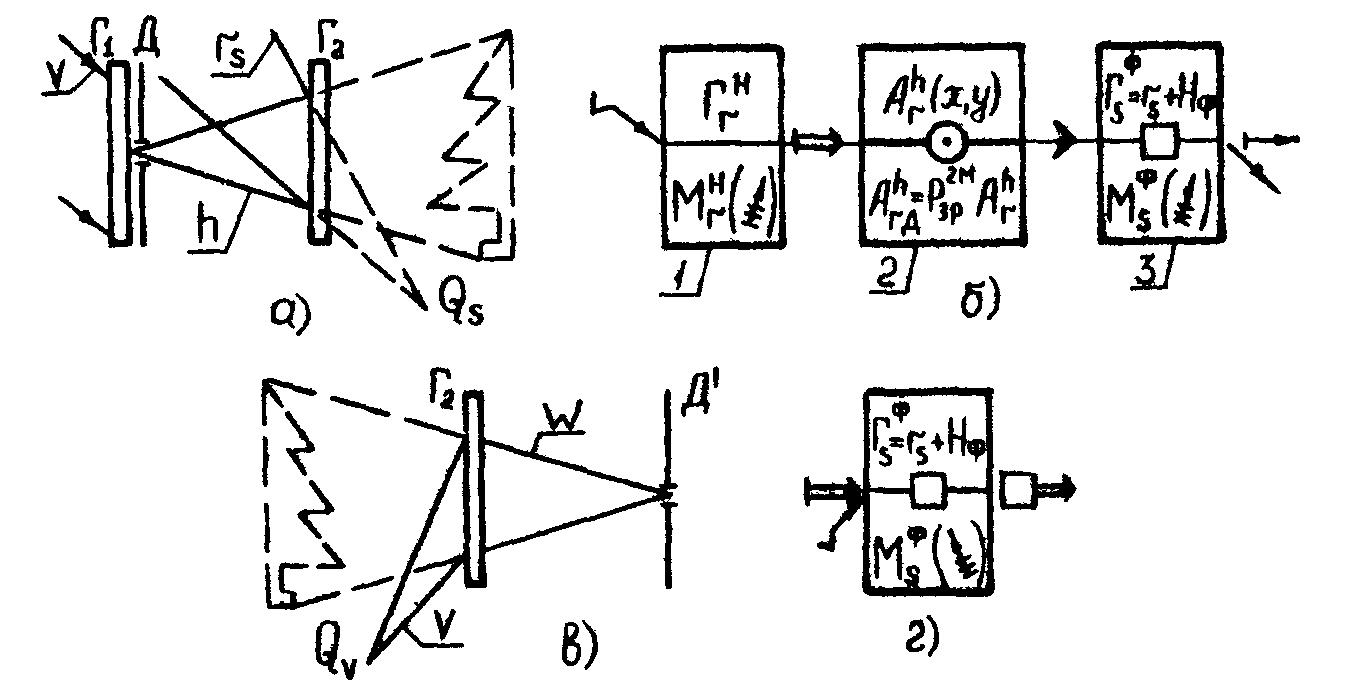
Рис.4.
Принципиальная схема записи радужной голограммы (рис.4б) состоит из трех блоков: 1 - вспомогательная голограмма Г1; 2 - диафрагма Д, действующая как мультипликативный амплитудный фильтр и определяющая функцию зрачка 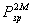 гoлoгpaммы; 3 - ра-
гoлoгpaммы; 3 - ра-
дужная голограмма Френеля, записанная на тонкой PC с амплитудной модуляцией. На рис.4г приведена принципиальная схема реконструкции радужной голограммы.
На рис.5а показана оптическая схема записи голограммы Фраунгофера с точечным опорным источником, расположенным в плоскости транспаранта Тр (квази-фурье-голограмма). Входной Тр с амплитудным пропусканием освещаемая плоской нормально падающей волной с амплитудой ар. Объектив Об, действующий как фазовый мультипликативный фильтр с пропусканием τоб, и СП Френеля осуществляют преобразование Фраунгофера входного сигнала. Точечный источник δ(υ-хр, 0) формирует опорную волну rs. Принципиальная схема (рис.5б) содержит предметную и опорную ветви и показывает, что регистрируется голограмма Фраунгофера Гsr со сферической расходящейся опорной волной. Так как опорный источник расположен в плоскости Тр, то матрица АsF принимает вид АpF, а голограмма Фраунгофера на стадии реконструкции обладает свойствами голограммы Фурье. Таким образом, квази-фурье-голограмма представляет собой Фурье-подобную голограмму Фраунгофера /2/:
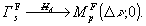
3. Объективные критерии качества и структурная модель
голографического процесса
Так как восстановленная волна используется для выполнения различных задач, то очевидно, что понятие качества во многом субъективно и изменяется в зависимости от назначения голограммы. Возможны по крайней мере, два подхода к оценке качества ГП, в которые вкладываются два на первый взгляд разных смысла. Во-первых, естественно считать, что высококачественное восстановленное голографическое изображение должно быть наиболее близко к регистрируемому волновому фронту. Иначе говоря, речь идет об оценке степени сходства голографируемого и восстановленного волновых фронтов. Во-вторых, когда восстановленное изображение
мало похоже на объект, то наилучшему качеству ГП соответствует максимальное количество информации, которое можно получить из восстановленной волны при заданном отношении сигнала к шуму. При этом и в том и в другом случае используется выработанное в СТГ понятие ТГ.
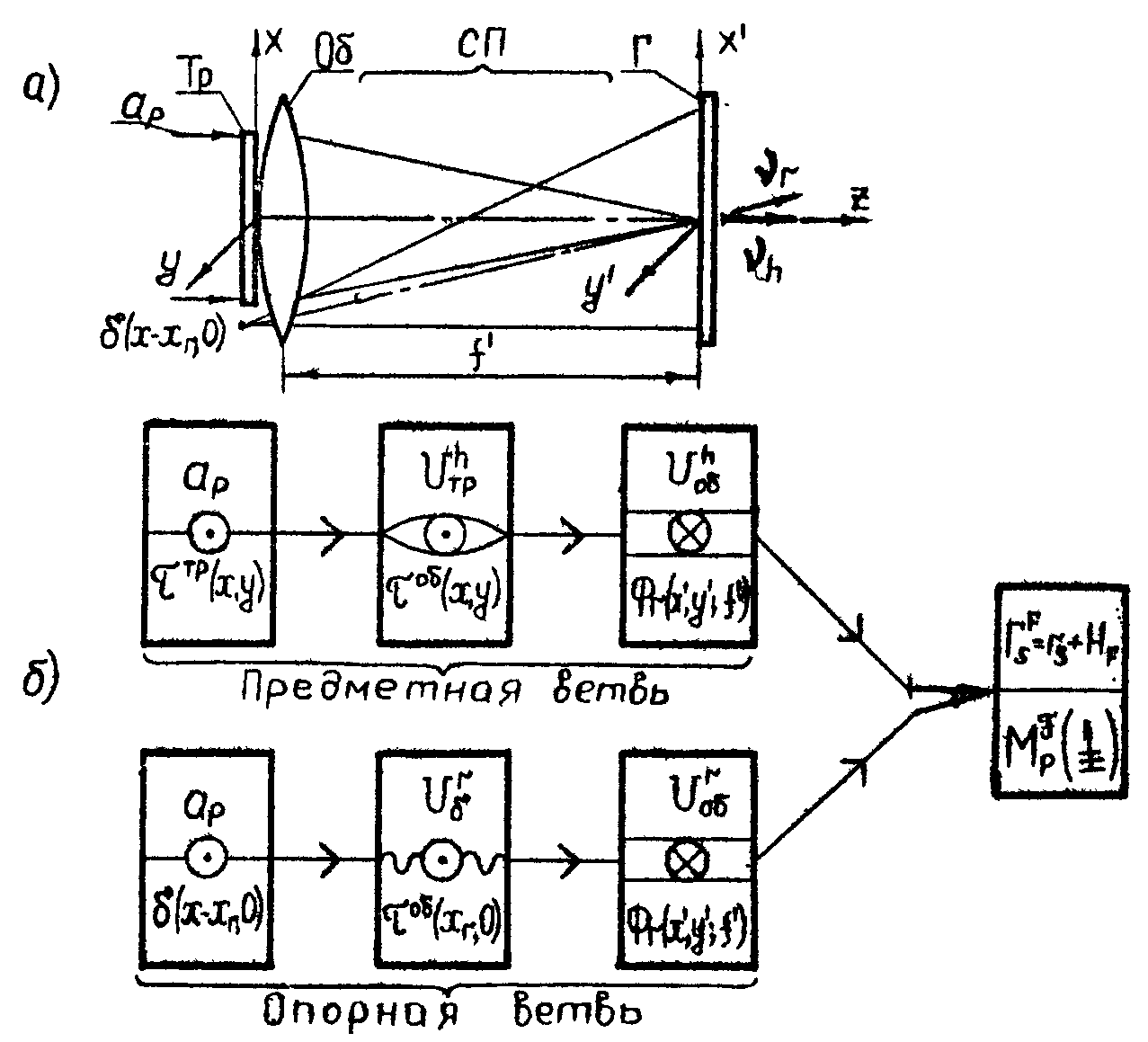
Рис.5.
3.1. Критерии качества как количественные оценки свойств
структурных преобразований
Каждый критерий качества оценивает количественно определенное свойство голографического или голограммного преобразования и связан с каким-то структурным элементом типа голограммы. При этом следует различать общие и частные критерии качества. Общие критерии качества полностью характеризуют один из основных элементов типа голограммы ГrH, 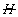 или МrH и выступают как количественные оценки преобразования, формирующего этот элемент. К частным критериям качества относятся дополнительные параметры, выделяющие какую-либо из сторон преобразования. Однако выработка любого критерия качества должна базироваться на основе СМ ОГЗ.
или МrH и выступают как количественные оценки преобразования, формирующего этот элемент. К частным критериям качества относятся дополнительные параметры, выделяющие какую-либо из сторон преобразования. Однако выработка любого критерия качества должна базироваться на основе СМ ОГЗ.
Голографический подтип ГrH характеризуется основным параметром - вектором пространственной несущей частоты 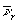 опорной волны, который определяет возможность углового разделения восстановленных ДП. Дополнительным параметром служит вектор
опорной волны, который определяет возможность углового разделения восстановленных ДП. Дополнительным параметром служит вектор 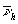 который задает расположение пространственного спектра объекта на частотной плоскости. Координата точек объекта Qh(xh,уh,zh) и опорного источника Qr(xr,yr,zr) позволяют охарактеризовать дифракционно-геометрическое преобразование поля, осуществляемое регистрирующей средой.
который задает расположение пространственного спектра объекта на частотной плоскости. Координата точек объекта Qh(xh,уh,zh) и опорного источника Qr(xr,yr,zr) позволяют охарактеризовать дифракционно-геометрическое преобразование поля, осуществляемое регистрирующей средой.
К одним из основных критериев качества ГП, которые оценивают влияние преобразующих свойств регистрирующей среды  на степень сходства исходного и восстановленного волнового фронта, можно отнести дифракционную эффективность η, коэффициент нелинейности kнл в передаче градаций яркости и отношение сигнал/шум S/N. Эти три характеристики в силу единой параметризации процесса регистрации взаимосвязаны друг с другом с помощью некоторой совокупности параметров. Соответствующая зависимость индуцируется свойствами голографического оператора
на степень сходства исходного и восстановленного волнового фронта, можно отнести дифракционную эффективность η, коэффициент нелинейности kнл в передаче градаций яркости и отношение сигнал/шум S/N. Эти три характеристики в силу единой параметризации процесса регистрации взаимосвязаны друг с другом с помощью некоторой совокупности параметров. Соответствующая зависимость индуцируется свойствами голографического оператора 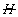 и геометрически интерпретируется в виде пространственной параметрической кривой kнл-η-S/N.
и геометрически интерпретируется в виде пространственной параметрической кривой kнл-η-S/N.
Главными характеристиками голографического изображения на стадии восстановлении являются ДП. При задании восстанавливающих свойств голограммы реконструирующим оператором R(Аrh) коэффи-
циенты с11, с12 и с21, с22 служат для оценки объемных отражательно-пропускающих свойств голограммы. Для идеальной тонкой (плоской) голограммы с11=с12=1, с21=с22=0. В случае объемной голограммы один из коэффициентов cmn=0. Экспериментальное определение зависимости cmn и c11/c12 от угла падения восстанавливающей волны в связи между ними позволит оценить нелинейные искажения, обусловленные толщиной регистрирующей среды. Появление дифрагированных волн второго и более высокого порядка описывается аддитивной диагональной матрицей, след которой равен решетке соответствующего порядка. Для оценки разрешающей способности матрица амплитудного пропускания умножается на функцию зрачка голограммы, которая определяет одно и то же предельное разрешение в каждом ДП.
3.2. Дифракционная эффективность фурье-голограмм
Понятие типа голограммы дает возможность не только сравнивать между собой различные критерии качества в зависимости от основных параметров типа и тем самым находить оптимальные параметры типа, но и корректно подходить к применению этих критериев. Рассмотрим это на примере дифракционной эффективности (ДЭ), равной отношению светового потока РW в восстановленном ДП к световому потоку РV, падающему на голограмму на стадии восстановления, так что η=PW/PV. ДЭ является интегральной энергетической характеристикой голограммы, а ее значения в разных участках голограммы зависят от интерференционной структуры. Только в случае голограммы двух плоских волн, обладающей однородной интерференционной структурой, ДЭ можно найти как не зависящее от площади голограммы Sr отношение соответствующих интенсивностей
η=IW/IV. (7)
В общем случае голографический подтип ГrH=r+Н представляет собой некоторую совокупность полей, комплексные амплитуды которых сложным образом изменяются в плоскости регистрирующей среды. После экспонирования это приводит к возникновению неоднородной интерференционной картины с различными восстанав-
ливающими свойствами в разных участках голограммы. Это требует расширения понятия ДЭ путам введения удельной ДЭ, равной ДЭ единицы площади голограммы. Эта величина называется дифракционностью, имеет размерность [M-2], обозначается греческой буквой ипсилон υ и с учетом (7) имеет вид
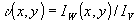 . (8)
. (8)
Тогда ДЭ голограммы любого типа теоретически может быть найдена как средняя дифракционность
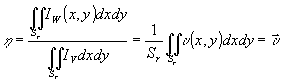 . (9)
. (9)
В частности, для голограммы двух плоских волн дифракционность совпадает с ДЭ (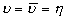 ). Таким образом, введение дифракционности позволяет устанавливать связь между разрешающей способностью и световым КПД голограммы, обусловленную ее размерами. При этом в качестве основной энергетической характеристики для теоретического сравнения восстанавливающих свойств произвольных типов голограмм должна использоваться величина средней дифракционности
). Таким образом, введение дифракционности позволяет устанавливать связь между разрешающей способностью и световым КПД голограммы, обусловленную ее размерами. При этом в качестве основной энергетической характеристики для теоретического сравнения восстанавливающих свойств произвольных типов голограмм должна использоваться величина средней дифракционности 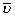 .
.
В качестве примера ограничимся анализом дифракционности фурье-голограмм. Структурный подход выделяет общее понятие фурье-голограммы 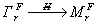 /2/. Оно является обобщением классической фурье-голограммы и отражает специфику кодирования фурье-образа как с помощью плоской rp, так и сферической rs опорной волны, что обуславливает различные значения
/2/. Оно является обобщением классической фурье-голограммы и отражает специфику кодирования фурье-образа как с помощью плоской rp, так и сферической rs опорной волны, что обуславливает различные значения 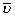 . В общем случае фурье-образ в плоскости голограммы представляет собой сумму плоских волн с амплитудами hpk, определяемыми значениями поля в точках объекта. Тогда матрицу амплитудного пропускания фурье-голограммы предметной волны
. В общем случае фурье-образ в плоскости голограммы представляет собой сумму плоских волн с амплитудами hpk, определяемыми значениями поля в точках объекта. Тогда матрицу амплитудного пропускания фурье-голограммы предметной волны 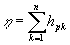 , с плоской опорной волной rp голографического типа
, с плоской опорной волной rp голографического типа
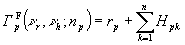 (рис.6.)
(рис.6.)
можно представить в виде
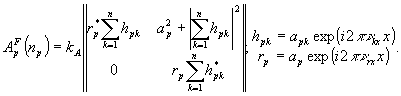 (10)
(10)
Откуда для матрицы средних дифракционностей трех ДП получим
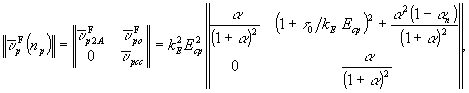 (11)
(11)
где
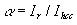 ;
; 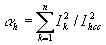 ;
; 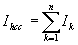 .
.
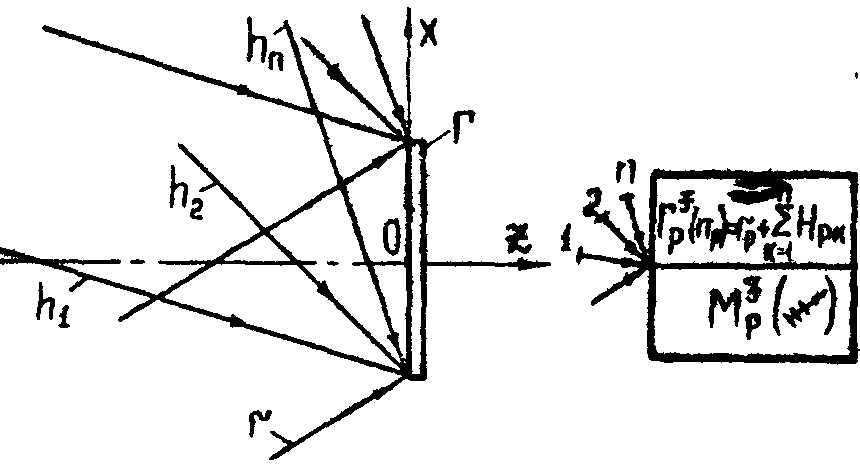
Рис.6.
Для элементарной фурье-голограммы со сферической опорной волной голографический подтип имеет вид 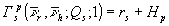 (рис.7). Если вектор
(рис.7). Если вектор 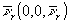 направлен вдоль оси z, то
направлен вдоль оси z, то
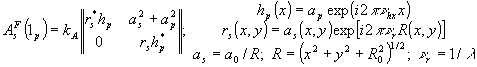 (12)
(12)
Тогда для матрицы средних дифракционностей найдем
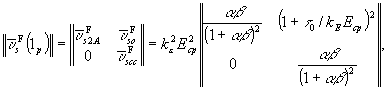 (13)
(13)
где
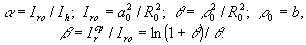 (14)
(14)
Откуда для приведенной средней дифракционности имеем:
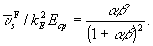 (15)
(15)
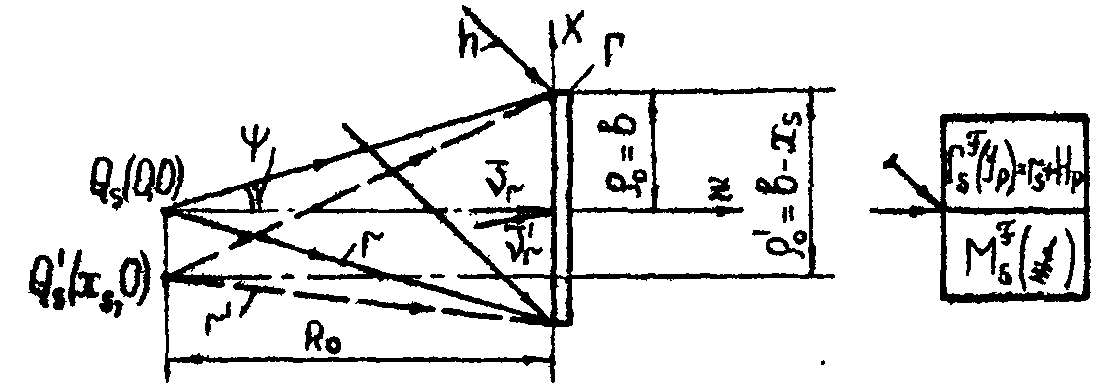
Рис.7.
Наклонное падение сферической опорной волны (рис.7), задаваемой характеристическим вектором 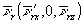 , обуславливает соответствующее выражение для коэффициента β в (16), так что
, обуславливает соответствующее выражение для коэффициента β в (16), так что
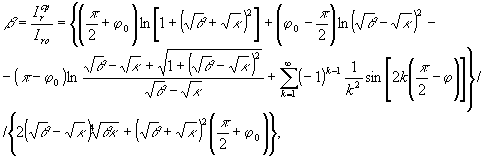 (16)
(16)
где
θ=b2/R02; κ=κs2/R02; ρ0'=2(b-xs); tgφ0=xs/ρ0'.
Зависимости средней дифракционности от параметра α приведена на рис.6 (кривые I для β по формуле (14) и кривые II для β - по (16) рассчитаны и построены Т.М.Волосатовой).
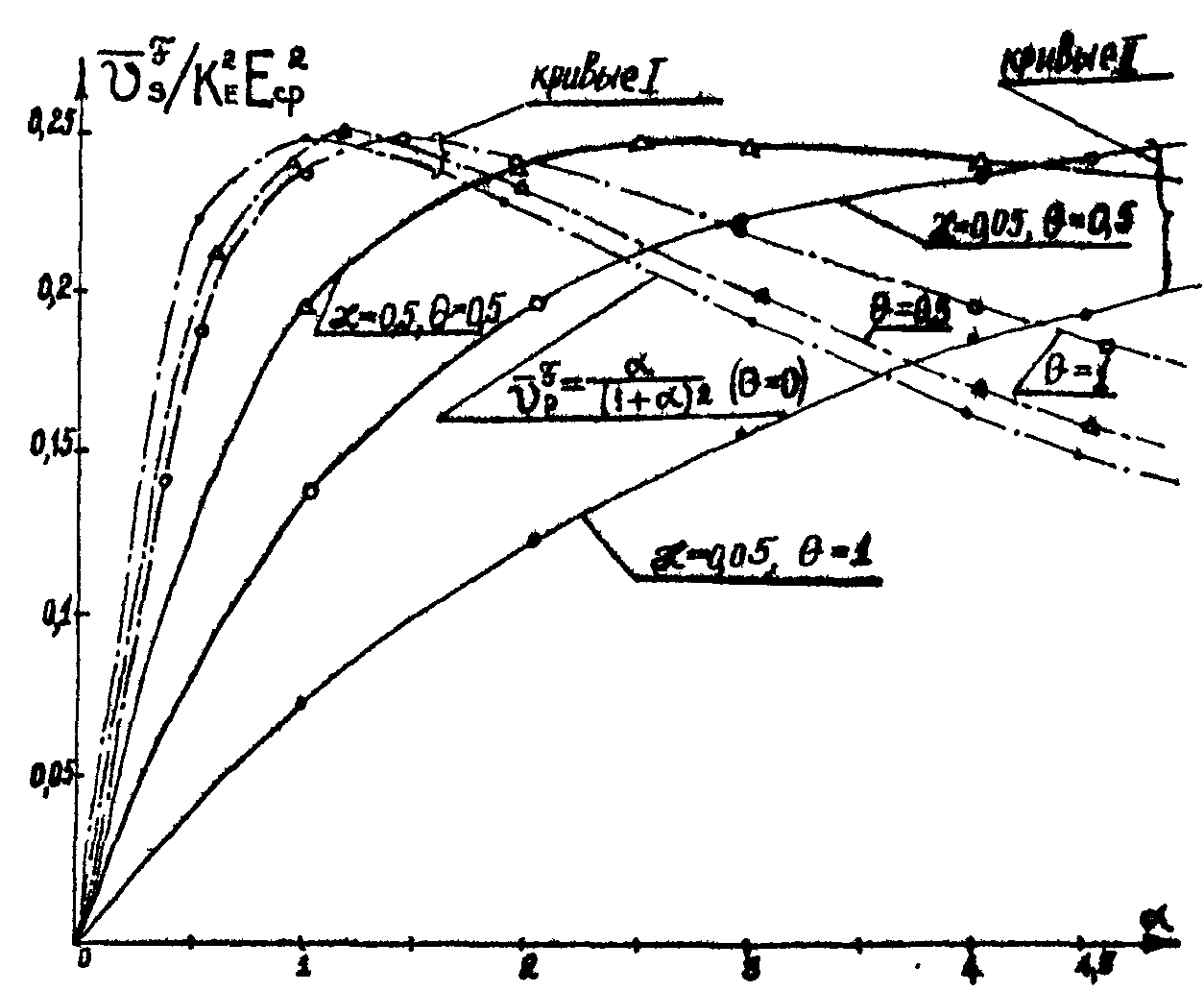
Рис.8.
Л и т е р а т у р а
1. В.Б.Немтинов. Структурная теория голографического процесса. В сб. "Оптико-электронные приборы", МВТУ, М., стр.123-138, 1979.
2. Г.М.Мосягин, В.Б.Немтинов. Преобразование сигналов в оптико-электронных приборах систем управлений летательными аппаратами, М., "Машиностроение", 1980.
3. М.С.Соскин. Динамическая голография и преобразование лазерных пучков. В сб."Фундаментальные основы оптической памяти и среды", КГУ, "Вища школа", К., стр.3-21, 1978.
4. Б.Я.Зельдович, В.И.Поповичев и др. О связи между волновыми фронтами отраженного и возбуждающего света при вынужденном рассеянии Мандельштама-Бриллюэна. Письма в ЖЭТФ, т.15, стр.160, 1972.
5. Ю.Н.Денисюк. Состояние и перспективы голографии с записью в трехмерных средах. В сб. "Оптическая голография", Л.."Наука", стр.5-23, 1979.
6. Ю.Н. Денисюк.Об отображениях оптических свойств объекта в волновом поле рассеянного им излучения, ДАН СССР, т.144, вып.6, стр.1275-1278, 1962.
7. H.Kogelnik. Coupled wave theory of thich hologram gratings The Bell System Techn. Journ., v.48, 9, 2909, 1969.
8. В.Г.Сидорович. О дифракционной эффективности трехмерных голограмм, ЖТФ, т.46, вып.6, стр.1306-1313, 1976.
9. Б.Н.Зельдович, В.В.Шкупов. Модовая теория объемных голограмм. В сб."Физические основы голографии" (Материалы Х Вс.школы по голографии), Л., стр.46-84, 1978.
10. В.И.Мандросов, И.П.Налимов, Ю.Н.Овечкис, И.У.Федчук, А.Х.Шакиров. О пропускающих и отражающих свойствах голограмм, записанных на встречных и сопутствующих пучках. ЖНИФК, т.22, стр.129-131, 1977.
11. О.Б.Серов, А.М.Смолович, Г.А.Соболев. Общность свойств голограмм, зарегистрированных на сходящихся и встречных пучках. В сб. "Оптическая голография", Л., "Наука", стр.122-128, 1979.
12. П.Г.Власов, Р.В.Рябова, С.П.Семенов. Голограммы Лейта, восстанавливаемые в белом свете. В сб."Голографические методы исследований" (Материалы Х Вс.школы по голографии), Л., стр.42-55, 1978.

