|
|
 |
 |

|
| |
УДК 535
ТЕОРИЯ ВОССТАНОВЛЕНИЯ ПОЛЕЙ ОБЪЕМНЫМИ ГОЛОГРАММАМИ
И СПЕКТРАЛЪНОУГЛОВЫЕ ИСКАЖЕНИЯ
Н.Б.Баранова, Б.Я.Зельдович, В.В.Шкунов, Т.В.Яковлева
ЧАСТЬ I
ОСНОВНЫЕ УРАВНЕНИЯ И МЕТОДИКА ИХ РЕШЕНИЯ
Модовая теория объемных голограмм сформулирована в терминах связанных пространственно-неоднородных волн. В процессе распространения опорной волны но голограмме генерируется не только структура неискаженного поля объемной волны, но и ее поперечные производные различных порядков. Для z - зависящих коэффициентов при этих структурах (где z -координата по нормали к поверхности голограммы) в рамках кодовой теории получена система связанных уравнений. В стандартном приближении кодовой теории производные структуры опускаются, и это позволяет рассчитать дифракционную эффективность и угловую, спектральную и пр. селективности объемных голограмм. Учет производных структур позволил найти спектрально-угловые искажения объемной волны в процессе восстановления для наиболее общего случая амплитудно-фазовых, просветных и отражательных объемных голограмм с высокой дифракционной эффективностью. Интенсивность этих искажений оказывается в основном пропорциональной квадрату угловой расходимости объемной волны.
По сравнению с тонкими голограммами Габора /1/ и Лейта и Упатниекса /2/ объемные голограммы (ОГ) Ю.Н.Денисюка /3/ обладают целым рядом преимуществ. Сюда относятся возможность восстановления тепловыми источниками света, обусловленная высокой спектрально-угловой селективностью, низкий уровень интрамодуляционных шумов, подавление сопряженных изображений и потенциально высокая дифракционная эффективность. В тех же пионерских работах /3/ был дан и первый вариант теории ОГ, основанный на рассмотрении борновского приближения для скалярной задачи восстановления объектного поля с относительно узким угловым спектром. По самому смыслу борновского приближения, оно не позволяет опи-
сать ОГ с высокой (порядка 1) дифракционной эффективностью. В широко известной работе Когельника /4/ для выхода за рамки борновского приближения была рассмотрена сильно упрощенная задача о дифракции волн на синусоидальной объемной решетке диэлектрической проницаемости; это соответствует случаю, когда и объектная, и опорная волны являются плоскими. Ввиду нелинейной зависимости амплитуды восстановленного поля от амплитуд индивидуальных плоских угловых компонент реального (т.е.широкоугольного) объектного поля результаты работы /4/ непосредственно не приложимы к большинству экспериментальных задач. Тем не менее, важнейшим достижением работы /4/ явилось внесение метода связанных волн (в данном случае - плоских) в теоретическую голографию.
Поле реальной объектной волны 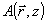 как при записи, так и при восстановлении в ОГ, обладает мелкомасштабной спекл-структурой, обусловленной интерференцией различных угловых компонент, см.рис.1. Для существенно объемных голограмм эти неоднородности спекл-структуры успевают много раз смениться на толщине голограммы L, условие этого как при записи, так и при восстановлении в ОГ, обладает мелкомасштабной спекл-структурой, обусловленной интерференцией различных угловых компонент, см.рис.1. Для существенно объемных голограмм эти неоднородности спекл-структуры успевают много раз смениться на толщине голограммы L, условие этого
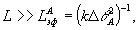 (1) (1)
собственно говоря, и является критерием объемности голограммы в нашей терминологии. Здесь k=ωn/c - волновое число, ΔθА - угловая расходимость объектной волны А. Заметим, что даже при нарушении условия (1) на толщине голограммы все еще может укладываться большое число полос от интерференции δε~AB*+A *B объектного поля А с опорным В (кросс-модуляционные возмущения); это более типично для отражательных голограмм, где период интерференции 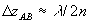 . Голограммы с . Голограммы с 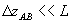 < <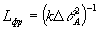 мы будем называть не объемными, а толстослойными, такие голограммы, как известно, дают довольно значительное искажение при восстановлении, см.например /5/. мы будем называть не объемными, а толстослойными, такие голограммы, как известно, дают довольно значительное искажение при восстановлении, см.например /5/.
Реальная задача распространения света при восстановлении достаточно сложна из-за наличия в ОГ быстро изменяющихся в пространстве возмущений, как интрамодуляционных, 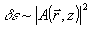 , так к кросс-модуляционных, , так к кросс-модуляционных, 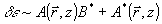 . Эксперимент, . Эксперимент,
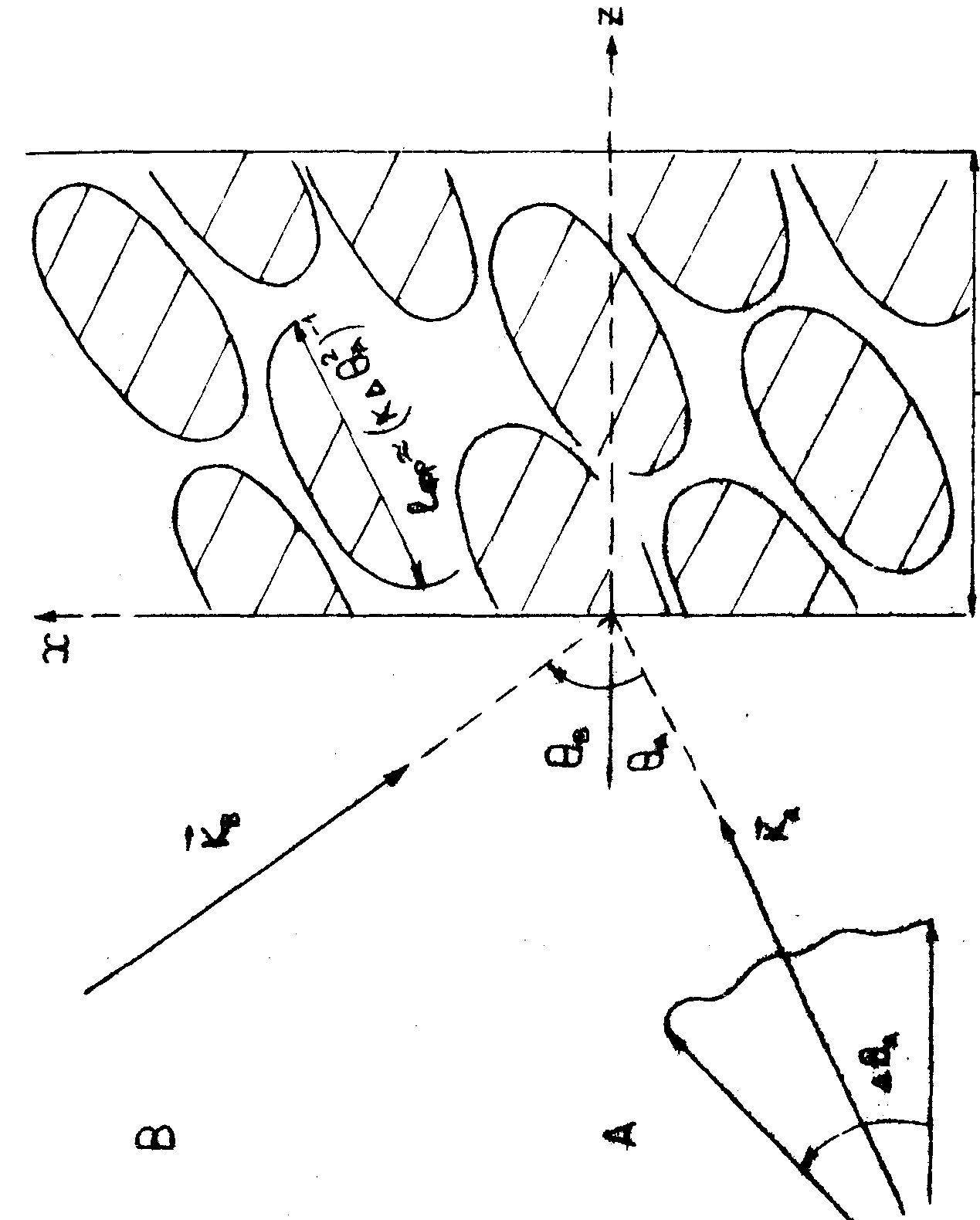
Рис.1. Картина возмущений диэлектрической проницаемости при записи просветной объемной голограммы плоской опорной волной В и спекл-неоднородной (кодированной) объемной волной 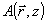 . .
однако, показывает, что с результате действия ОГ поле объекта, во крайней мере в определенных условиях, может быть восстановлено довольно точно, т.е. почти без искажений. Это наводит на мысль о том, что даже по такой среде пространотвенно-неоднородная водна a(z)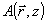 может идти без искажений (т.е. как будто по однородной среде) и вдоль по z меняется лишь ее общая амплитуда a(z) при сохранения пространственной спекл-структуры может идти без искажений (т.е. как будто по однородной среде) и вдоль по z меняется лишь ее общая амплитуда a(z) при сохранения пространственной спекл-структуры 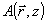 . Одновременно с этим должна меняться в амплитуда b(z) восстанавливающей опорной волны b(z) . Одновременно с этим должна меняться в амплитуда b(z) восстанавливающей опорной волны b(z)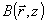 . Тем самым мы приходим к идее о паре связанных волн - a(z) . Тем самым мы приходим к идее о паре связанных волн - a(z)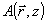 и b(z) и b(z)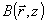 , но, вообще говоря, пространственно-неоднородных. , но, вообще говоря, пространственно-неоднородных.
Чрезвычайно важным шагом в направлении к такой картине действия ОГ явилась выдвинутая В.Г.Сидоровичем в работе /6/ мо-довая теория объемных голограмм *. В этой работе /6/ на примере параксиальной задачи о просветных фазовых голограммах было указано, что при статистически однородной по объему голограммы спекл-структуре записывающих полей существуют пространственные конфигурации 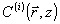 специального вида (моды голограммы), обладающие следующим свойством. Мода специального вида (моды голограммы), обладающие следующим свойством. Мода 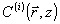 проходит через голограмму по законам дифракции в однородной среде, а эффект возмущений сводится лишь к множителю exp(iδki проходит через голограмму по законам дифракции в однородной среде, а эффект возмущений сводится лишь к множителю exp(iδkiz) , описывавшему поправку к фазовой скорости распространения. Среди найденных в /6/ мод были моды вида линейных комбинаций
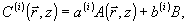 (2) (2)
которые и требовались для задачи о восстановлении объектного поля 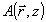 опорной волной В. На этом пути в /6/ удалось определять дифракционную эффективность параксиальной просветной фазовой ОГ как для плоской, так в для кодированной опорной волны опорной волной В. На этом пути в /6/ удалось определять дифракционную эффективность параксиальной просветной фазовой ОГ как для плоской, так в для кодированной опорной волны 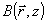 . .
В работе /8/ модоввя теория была впервые применена к задаче /9/ обращения волнового фронта при вынужденном рассеянии
света назад. В /8/ было показано, что условием существования "мод" в упомянутом выше смысле является выполнение сильного неравенства
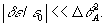 (3) (3)
Здесь |δ ε/ε0| - относительная амплитуда записанных в среде возмущений диэлектрической проницаемости.
В модовой теории /6/ поле внутри ОГ в процессе восстановления описывается суперпозицией двух (или большего чиола мод, например,
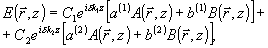 (4а)
где С 1 и С2 - амплитуда возбуждения мод, определяемые из граничных условий. Тождественное преобразование этого выражения в виду
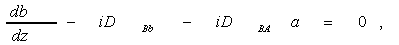 (4б)
показывает, что модовая теория во существу оперирует связанными волнами 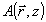 и и 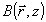 с z - зависящими коэффициентами a(z) и b(z). с z - зависящими коэффициентами a(z) и b(z).
Дальнейшее (и, с точки зрения авторов, весьма успешное) развитие модовой теории ОГ в работах /10-22/ велось как в исходных терминах "мод", так и в терминах, связанных проотранственно-неоднородных волн. На этом пути было рассмотрено большое число различных свойств ОГ, таких, как угловая и спектральная селективности, влияние усадки, поляризационные свойства и многие другие, были получены количественные выражения для величины интрамодуяяционных искажений, малость которых определяет применимость модовой теории.
Изменение условий при восстановлении ОГ по сравнению с условиями при записи (например, изменение частоты в направления
опорной волны, усадка материала и т.п.) влечет за собой не только изменение дифракционной эффективности, но и появление искажений в восстановленном поле по сравнению с исходным полем объекта. Расчет искажений из-за частотного сдвига для параксиальных просветит чисто фазовых голограмм впервые был проведен в работе /10/ в рамках модовой теории ОГ, и притом в терминах мод.
В настоящей работе методы модовой теории ОГ применены для единого рассмотрения искажений восстановленного поля, обусловленных изменением практически всех возможных условий восстановления по сравнению с условиями при записи. При этом переход к языку связанных пространственно-неоднородных волн не только повысил (по нашему мнению) наглядность изложения, но и позволил отказаться от ограничений параксиальности и фазового характера записанных возмущений, ограничений, характерных для языка "мод" /6,10,12-15/. Главный вывод из проведенного рассмотрения состоит в том, что интенсивность искажений пропорциональна квадрату параметров, характеризующих изменение условий в ОГ при восстановлении, и квадрату угловой расходимости объектной волны.
Система исходных электродинамических уравнений
Мы предположим, что в процессе записи по фоточувствительной среде толщиной L с диэлектрической проницаемостью ε0 распространяется монохроматическое поле частоты ω0 с вектором комплексной амплитуды:
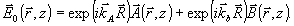 (5) (5)
Здесь 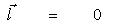 , ,  . .
В процессе обработки экспонированной голограммы обычно происходит усадка материала по координате z, нормальной к поверхности голограммы. При этом координата z' данного материального носителя информации до обработки связана с его координатой z после обработки соотношением
z'=z(1+ρ), (6)
где ρ=(L0-L)/L 0<<1 - параметр, характеризующий относительную величину усадки. Волну 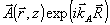 мы называем объектной, а волну мы называем объектной, а волну 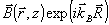 - опорной. В большинстве случаев поле объектной волны обладает развитой спекл-отруктурой из-за интерференции различных составляющих ее угловых компонент (т.е. волна А - кодированная). Опорная волна - опорной. В большинстве случаев поле объектной волны обладает развитой спекл-отруктурой из-за интерференции различных составляющих ее угловых компонент (т.е. волна А - кодированная). Опорная волна 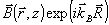 может быть как кодированной, так и плоской; в последнем случае может быть как кодированной, так и плоской; в последнем случае 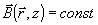 . В задачах голографической коррекции лазерных пучков плоской является именно объектная волна . В задачах голографической коррекции лазерных пучков плоской является именно объектная волна 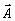 . В дальнейшем нам понадобятся величины fA и fB, которым мы приписываем значения . В дальнейшем нам понадобятся величины fA и fB, которым мы приписываем значения
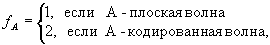 (7) (7)
аналогично для B - волны. Поле 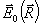 так же, как и каждая из волн так же, как и каждая из волн 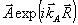 и и 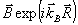 , удовлетворяет волновому уравнению , удовлетворяет волновому уравнению
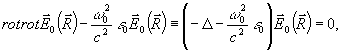 (8) (8)
при этом мы использовали, что
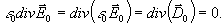
В результате экспозиции и обработки диэлектрическая проницаемость в точке голограммы с координатами 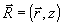 принимает значение принимает значение
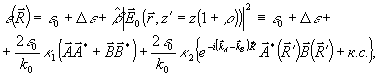 (9) (9)
где 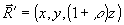 , и множитель (1+ρ) при координате z описывает эффект усадки. Здесь величина Δε υарактеризует "оптическое уплотнение" обработанной голограммы в отсутствие экспозиции. Коэффициент передачи мы считаем различным дня интрамодуляционных возмущений , и множитель (1+ρ) при координате z описывает эффект усадки. Здесь величина Δε υарактеризует "оптическое уплотнение" обработанной голограммы в отсутствие экспозиции. Коэффициент передачи мы считаем различным дня интрамодуляционных возмущений 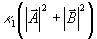 , и дня кросс-модуляцион- , и дня кросс-модуляцион-
ных слагаемых, 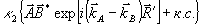 . Это позволяет описать действие частотно-контрастной характеристики материале, причем обычно |κ2|<|κ1 . Это позволяет описать действие частотно-контрастной характеристики материале, причем обычно |κ2|<|κ1| из-за наличия быстрой пространственной зависимости 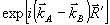 в кросс-модуляционных членах. Введение множителя 2ε0 в кросс-модуляционных членах. Введение множителя 2ε0/k 0 определяется соображениями удобства. Мы предполагаем отклик среды скалярным (о средах с нескалярной записью см. /11/) и линейным по интенсивности записывавшего поля (модовая теория ОГ с учетом нелинейности фотопроцесса сформулирована в работе /20/). В общем случае все три величины - Δε, κ1 и κ2 - комплексны, для чисто фазовых голограмм κ1 и κ2 вещественны, а для чисто амплитудных величины κ1 и κ2 чисто мнимы.
Пусть в процессе восстановления на гслограмму падает восстанавливающая опорная волна частоты ω, в общем случае отличающейся от частоты ω 0 при записи. Волновое уравнение для восстанавливающего поля 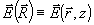 имеет вид имеет вид
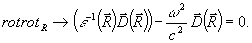 (10) (10)
Здесь мы ввели вектор индукции 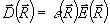 , причем с линейной точностью по возмущениям , причем с линейной точностью по возмущениям 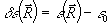 имеем имеем
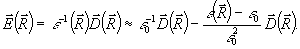 (11) (11)
Используя условие поперечности индукции 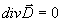 , из (10) нетрудно получить уравнение , из (10) нетрудно получить уравнение
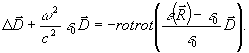 (12) (12)
При переходе от (10) к (12) мы отбросили слагаемые ~(ε-ε0) 2 и более высоких порядков малости по (ε-ε0). Разумеется, вто еще не означает, что мы используем борновское приближение. Как будет видно из дальнейшего, даже при малой величине |(ε-ε0)/ε0|<<1 параметр |ε-ε0|ωL/c может быть большим. Это связано с тем обстоятельством, что для длины волны λвак=0,5 мкм и типичных толщин голограммы L~10÷30 мкм величи-
на ωL/с=2πL/λвак составляет ~30÷100, что компенсирует малость величины |ε-ε0|. Поэтому решать приближенное уравнение (12) следует с учетом всех порядков по параметру |ε-ε0|ωL/c, но c использованием малости величины |ε-ε0|. В дальнейшем о той же точностью уравнение (12) мы будем считать применимым и к полю 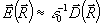 . .
В отношении граничных условий мы предположим, что в процессе восстановления на поверхность z= 0, L падает считывающая опорная волна 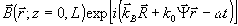 , которая по своей поперечной структуре отличается от записывавшего опорного поля множителем , которая по своей поперечной структуре отличается от записывавшего опорного поля множителем 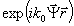 . Если ω=ω0, то этот множитель описывает изменение угла считывающей опорной волнь по сравнению с записывавшей. При |ω-ω0 . Если ω=ω0, то этот множитель описывает изменение угла считывающей опорной волнь по сравнению с записывавшей. При |ω-ω0|≠0 величина 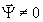 и содержит слагаемые Ψ~(ω-ω0 и содержит слагаемые Ψ~(ω-ω0) даже в отсутствие поворота опорной волны при восстановлении. Введение фактора 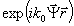 позволяет рассмотреть задачу об угловой и спектральной селективности ОГ; подробное исследование этого вопроса см. в /16/. позволяет рассмотреть задачу об угловой и спектральной селективности ОГ; подробное исследование этого вопроса см. в /16/.
Следует также специально обсудить вопрос о количестве граничных условий. Как известно, для дифференциальных уравнений 2-го порядка (оператор Лапласа в (12) необходимо задание двух граничных условий - на саму функция и на ее нормальную производную (или на поля 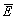 и и 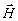 ). В задаче о падении света на границу между двумя однородными средами с проницаемостями ε1 и ε2 это позволяет определить амплитудный коеффициент френелевского отражения r~(ε1-ε2 ). В задаче о падении света на границу между двумя однородными средами с проницаемостями ε1 и ε2 это позволяет определить амплитудный коеффициент френелевского отражения r~(ε1-ε2). Везде в дальнейшем мы будем пренебрегать эффектами френелевского отражения, считая, например, голограмму погруженной в однородную иммерсную среду с проницаемостью ε0. В пренебрежении малыми поправками порядка |ε-ε0|/ε0 мы можем нe учитывать и поверхностного френелевского отражения с r~ε-ε0. В то же время объемные эффекты порядка (ε-ε0)∙ωL/с мы будем учитывать по ввзможности точно. В рамках сделанных выше приближений оказывается достаточным задать лишь одно граничное условие. Для просветиой голограммы оно имеет вид:
 (13) (13)
а для отражательной голограммы граничные условия должны быть заданы в сечениях z=0 и z=L, см.раздел 5. Ниже наиболее подробно будет рассмотрен случай плоской опорной волны, 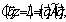 , а объектное поле , а объектное поле 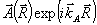 будем считать кодированным, т.е. обладающим мелкомасштабной спекл-структурой. будем считать кодированным, т.е. обладающим мелкомасштабной спекл-структурой.
Искажения в борновском приближении
Здесь на простейшем примере мы рассмотрим структуру возможных искажений, возникающих при восстановлении поля в ОГ. Пусть голограмма записана плоской опорной волной 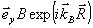 и объектной волной и объектной волной 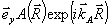 . Для определенности в этом разделе мы считаем, что центральное направление . Для определенности в этом разделе мы считаем, что центральное направление 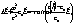 объектной волны и направление объектной волны и направление 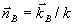 опорной волны лежат в плоскости хz, а поляризация обоих полей с нужной точностью может быть взята в виде постоянного орта опорной волны лежат в плоскости хz, а поляризация обоих полей с нужной точностью может быть взята в виде постоянного орта 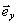 , перпендикулярного плоскости чертежа на рис.2. Будем считать, что изменение частоты, угловой сдвиг, усадка и оптическое уплотнение отсутствуют. Кроме того, пусть восстанавливающая волна также имеет у-поляризацию, , перпендикулярного плоскости чертежа на рис.2. Будем считать, что изменение частоты, угловой сдвиг, усадка и оптическое уплотнение отсутствуют. Кроме того, пусть восстанавливающая волна также имеет у-поляризацию, 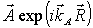 . В борновском приближении в правой части уравнения (12), . В борновском приближении в правой части уравнения (12),
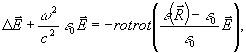 (12a) (12a)
следует учесть лишь рассеяние невозмущенной опорной волны на кросс-модуляционных решетках δε~AB*, записанных в ОГ. При этом для поля 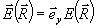 получим уравнение получим уравнение
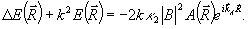 (14) (14)
Исходное поле 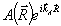 , а также решение уравнения (14) удобно представить с помощью разложения в интеграл или ряд Фурье по поперечным координатам, , а также решение уравнения (14) удобно представить с помощью разложения в интеграл или ряд Фурье по поперечным координатам, 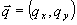 . .
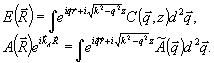 (15) (15)
Ввиду того, что поле 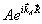 при записи удовлетворяет однородному волновому уравнению (8), фурье-амплитуды при записи удовлетворяет однородному волновому уравнению (8), фурье-амплитуды 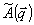 не зависят от координаты z. Подстановка (15) в (14) дает не зависят от координаты z. Подстановка (15) в (14) дает
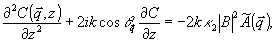 (16) (16)
где введено обозначение
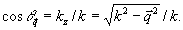 (17) (17)
Сделаем предположение (законность которого при kL<<1 оправдывается результатагяи расчета) о том, что вторую производную в (16) можно опустить. Тогда
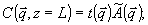 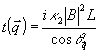 . (18) . (18)
Параметр 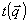 есть амплитудный коэффициент восстановления есть амплитудный коэффициент восстановления 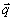 -ой компоненты углового спектра объектного поля А. Появление величины -ой компоненты углового спектра объектного поля А. Появление величины 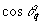 в знаменателе имеет простой смысл. Именно, в борновском приближении амплитуда восстановленной волны пропорциональна длине пути L' в среде, на протяжении которого когерентно накапливаются рассеянные кросс-решеткой волны, причем ддя данной угловой компоненты в знаменателе имеет простой смысл. Именно, в борновском приближении амплитуда восстановленной волны пропорциональна длине пути L' в среде, на протяжении которого когерентно накапливаются рассеянные кросс-решеткой волны, причем ддя данной угловой компоненты 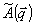 имеем L'=L/cos имеем L'=L/cos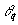 . .
Если угловая расходимость объектного поля невелика, то в самом грубом приближении функцию 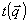 в пределах углового спектра в пределах углового спектра 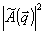 можно считать постоянной и равной можно считать постоянной и равной 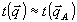 , где , где 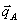 отвечает некоторому центральному направлению волны А. В этом приближении объектная волна восстанавливается без искажений, т.е. с точностью до общего множителя отвечает некоторому центральному направлению волны А. В этом приближении объектная волна восстанавливается без искажений, т.е. с точностью до общего множителя 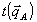 имеет ту же структуру, что и при записи. имеет ту же структуру, что и при записи.
Учет зависимости 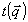 приводит к тому, что разные угловые компоненты передаются с разным весом. Восстановленное поле приводит к тому, что разные угловые компоненты передаются с разным весом. Восстановленное поле
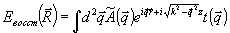 (19) (19)
мы представим в виде неискаженной объектной волны с подходящим коэффициентом, а остальной частью поля Евосст (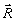 ), т.е. искажениями, мы будем называть часть, ортогональную к объектной волне. Тогда ), т.е. искажениями, мы будем называть часть, ортогональную к объектной волне. Тогда
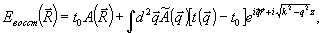 (20а)
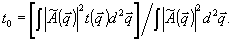 (20б)
Отношение полной интенсивности искаженной части волны к "правильной" определяет долю искажений Ф:
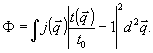 (21) (21)
Здесь мы ввели нормированное распределение интенсивности в объектной волне по 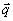 - компонентам: - компонентам:
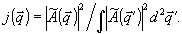
При этом 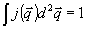 и, кроме того, и, кроме того, 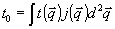 . Если угловая ширина объектного поля невелика, то величину . Если угловая ширина объектного поля невелика, то величину 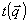 можно разложить вблизи некоторого центрального направления: можно разложить вблизи некоторого центрального направления:
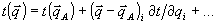
При этом 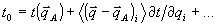 , где угловыми скобками обозначено усреднение по нормированному , где угловыми скобками обозначено усреднение по нормированному 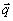 - спектру - спектру 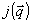 . В итоге доля искажений иа (21) с той же точностью равна . В итоге доля искажений иа (21) с той же точностью равна
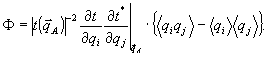 (22а)
Величина 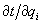 легко получается из (18): легко получается из (18):
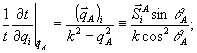

Если на голограмму из воздуха при записи падает волна А со среднеквадратичной угловой расходимостью 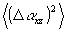 в воздухе в плоскости хz. (см. рис.2), то в воздухе в плоскости хz. (см. рис.2), то 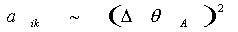 . В силу закона Снеллиуса поперечные компоненты волнового вектора не меняются при преломлении, и в результате доля искажений оказывается равной . В силу закона Снеллиуса поперечные компоненты волнового вектора не меняются при преломлении, и в результате доля искажений оказывается равной
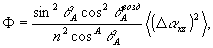 (22б)
где n - показатель преломления материала голограммы относительно воздуха. Возьмем численный пример с 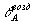 =45°, n=1,3, =45°, n=1,3, 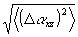 =23°=0,4 рад; при этом θA=33° и Ф=0,03, т.е. доля искажений составляет 3%. =23°=0,4 рад; при этом θA=33° и Ф=0,03, т.е. доля искажений составляет 3%.
Структура "ортогональных искажении" в (20а) может быть явно записана и в координатном пространстве:
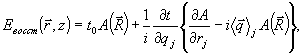
т.е. искажения состоят из производной от объектного поля 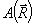 по поперечной координате х и самого поля по поперечной координате х и самого поля 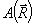 в такой линейной комбинации, которая обеспечивает ортогональность к полю в такой линейной комбинации, которая обеспечивает ортогональность к полю 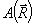 . .
Характер искажений в восстановленном поле (20) и (23) аналогичен тому, как еоли бы мы рассматривали объект через тонкую наклонную стеклянную пластину. Такая пластина вносят в пучок потери за счет френелевского отражения, причем кооэффициент пропускания зависит от угла. В результате разные части объекта, видные наблюдателю под разными углами, восстанавливаются с несколько различной амплитудой, в искажения заключаются именно в этом. Такой простой характер искажений здесь обусловлен тем, что обе величины – t0 и ¶
t/¶
qj - чисто вещественны и,
тем самым, имеют одинаковую фазу. Ниже, в разделе 7, мы получим дополнительные искажения восстановленного поля также в форме (23), но уже с произвольным соотношением фаз величин t0 и ¶
t/¶
qj.
Ясно, что при записи и (или) восстановлении волн с поляризацией в плоскости ( 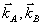 ) появятся дополнительные искажения того же порядка ( ) появятся дополнительные искажения того же порядка (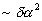 ), обусловленные вариациями ортов поляризации в пределах углового спектра. (Заметим, что для рассмотрения задачи с ), обусловленные вариациями ортов поляризации в пределах углового спектра. (Заметим, что для рассмотрения задачи с 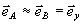 поляризационные искажения имеют меньшую интенсивность, ~(Δα)4 поляризационные искажения имеют меньшую интенсивность, ~(Δα)4).
Таким образом, в борновском приближении и при совпадении всех условий записи в восстановления искажения восстановленного в ОГ поля объекта А пропорциональны квадрату его угловой расходимости (Δ α)2, численно сравнительно невелики и имеют простую природу. Ниже, в разделе 7, мы рассмотрим искажения, обусловленные неодинаковостью условий при записи и восстановлении (спектральный сдвиг, усадка и т.п.). Эти искажения, также пропорциональные (Δα)2, в интересном случае оказываются заметно большими, чем шумы борновского приближения. По этой причине искажения, связанные с поляризацией, мы не будем конкретно рассматривать ни здесь, ни ниже, в разделе 7.
Приведем еще одну возможную интерпретацию механизма возникновения искажений восстановленного ОГ объектного поля в борновском приближении. В координатном представлении решение уравнения (14) может быть записано с помощью функции Грина уравнения Гельмгольца:
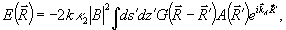 (24) (24)
где интегрирование ведется по площади голограммы ( ds') и по ее толщине (dz') и функция Грина 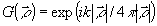 . Центральная идея объемной голографии /3/ основана на аналогии выражения (24) и выражения . Центральная идея объемной голографии /3/ основана на аналогии выражения (24) и выражения
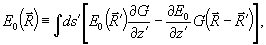 (25) (25)
для поля Е 0, подчиняющегося однородному уравнению Гельмгольца /см.21/. Для фурье-компонент поля А, характеризуемых утлом θА между волновым вектором и осью z, выражение (25) обычно приводят к приближенном форме:
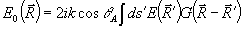 . (26) . (26)
Поскольку в принципе Гюйгенса плоскость z'=соnst может быть выбрана произвольно, то интегрирование (26) по dz' дает выражение вида (24). Таким образом, восстановленное в ОГ поле (24) с точностью до множителя 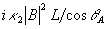 совпадает с тем полем объектной волны, которое было бы в точке совпадает с тем полем объектной волны, которое было бы в точке 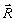 при распространении от объекта, согласно принципу Гюйгенса. Здесь фактор при распространении от объекта, согласно принципу Гюйгенса. Здесь фактор 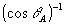 в точности соответствует такой же зависимости от угла для коэффициента в точности соответствует такой же зависимости от угла для коэффициента 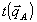 из (10). Однако, если объектная волна обладает достаточно широким угловым спектром, то переход от (25) к (26) не закончен, и в этом смысле восстановленное в ОГ поле (24) неточно воспроизводит поле (25), присутствовавшее при записи. из (10). Однако, если объектная волна обладает достаточно широким угловым спектром, то переход от (25) к (26) не закончен, и в этом смысле восстановленное в ОГ поле (24) неточно воспроизводит поле (25), присутствовавшее при записи.
Выше, в разделе 3, мы видели, что в процессе восстановления могут возникать искажения, имеющие структуру поперечных градиентов объектного поля. В этой связи поле в ОГ в процессе восстановления мы будем искать в виде суммы опорной и объектной волн и их поперечных производных различных порядков, причем коэффициенты при этих структурах меняются вдоль по толщине голограммы z. В наиболее интересном случае плоской опорной волны 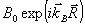 ее производные отличаются от исходной функции лишь множителем. Поэтому нам понадобятся лишь производные от поля объектной волны. В этом поле мы выделим быструю экспоненциальную зависимость, соответствующую некоторому центральному значению волнового вектора ее производные отличаются от исходной функции лишь множителем. Поэтому нам понадобятся лишь производные от поля объектной волны. В этом поле мы выделим быструю экспоненциальную зависимость, соответствующую некоторому центральному значению волнового вектора 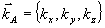 , где , где 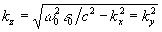 , т.e. полное поле объектной волны , т.e. полное поле объектной волны 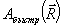 представим в виде представим в виде
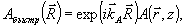
где 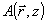 - сравнительно медленно меняющаяся амплитуда; характерный масштаб ее изменения - сравнительно медленно меняющаяся амплитуда; характерный масштаб ее изменения 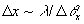 . Поле А образовано интерференцией большого числа невввиоямых угловых компонент и может рассматриваться как гауссовское (по статистике) случайное поле, которое мы будем характеризовать средними по ансамбле значениями. При этом <А>=0, и коррелятор равен . Поле А образовано интерференцией большого числа невввиоямых угловых компонент и может рассматриваться как гауссовское (по статистике) случайное поле, которое мы будем характеризовать средними по ансамбле значениями. При этом <А>=0, и коррелятор равен
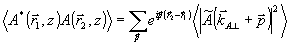 (27) (27)
(теорема Ван-Циттера-Цернике). Здесь величина 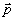 характеризует отличие характеризует отличие 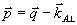 поперечной компоненты волнового вектора от его "центрального" значения поперечной компоненты волнового вектора от его "центрального" значения 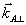 . Введем нормированное поле следующим определением . Введем нормированное поле следующим определением
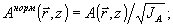 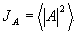 (28) (28)
Кроме того, для дальнейшего нам понадобится структура типа поперечных градиентов поля. В их определение удобно вносить множитель (- i/к) на каждую из производных, так что
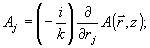 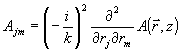 (29) (29)
и так далее. Функции Aj (j=1,2) в общем случае содержат проекцию как на поле 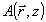 , так и друг на друга; например: , так и друг на друга; например:
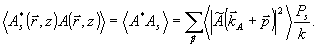 (30) (30)
Для этой величины удобно ввести специальное обозначение
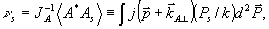 (31) (31)
где 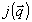 - нормированное распределение по значениям параметра - нормированное распределение по значениям параметра 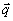 для интенсивности в объектной волне. Линейные комбинации для интенсивности в объектной волне. Линейные комбинации 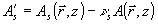 уже не содержат проекции на поле уже не содержат проекции на поле 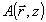 . (Заметим, что сам двумерный вектор . (Заметим, что сам двумерный вектор 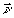 можно было бы обратить в нуль подходящим выбором центрального направления можно было бы обратить в нуль подходящим выбором центрального направления 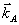 , ср.с формулой (27). Мы предпочитаем, однако, сохранять везде величины , ср.с формулой (27). Мы предпочитаем, однако, сохранять везде величины 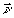 с тем, чтобы убеждаться в ковариантности получаемых выражений относительно небольших вариации конкретного выбора с тем, чтобы убеждаться в ковариантности получаемых выражений относительно небольших вариации конкретного выбора 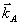 ). Тем не менее, две компоненты А'х и А'у ). Тем не менее, две компоненты А'х и А'у в общем случае не ортогональны и между собой:
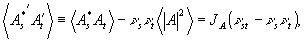 (32) (32)
где
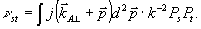 (31б)
Для ортогонализации и нормировки функций 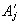 введем матрицу Nij (i, j пробегают значения х, у), введем матрицу Nij (i, j пробегают значения х, у),
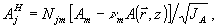 (33) (33)
такую, чтобы
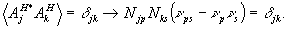 (34б)
Для случая, когда центральное направление объектной волны почти совпадает с осью z (т.е. с нормалью к поверхности голограммы), нам понадобится также учитывать и вторые производные объектного поля. Требуя ортогональности к функциям 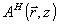 и и 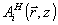 . Мы приходим к линейным комбинациям вида . Мы приходим к линейным комбинациям вида
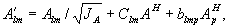 (35) (35)
где
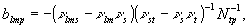 (36а)
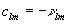 . (36б)
В силу симметрии по индексам l, m в (35) всего имеется 3 линейно-независимых функции. Их нормировку и ортогонализацию между собой мы произведем с помощью матрицы:
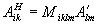 , (37а)
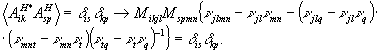 (37б)
В общем случае явное нахождение матриц 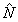 , , 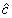 , , 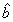 , , 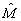 , осуществляющих приведение системы функцни к главным осям, является весьма сложной задачей. Замечательно, однако, что в окончательные результаты для интенсивности искажении (см. ниже раздел 7) входят лишь билинейные комбинации этих матриц, которые удается выразить по соотношениям (34), (36), (37б) через моменты , осуществляющих приведение системы функцни к главным осям, является весьма сложной задачей. Замечательно, однако, что в окончательные результаты для интенсивности искажении (см. ниже раздел 7) входят лишь билинейные комбинации этих матриц, которые удается выразить по соотношениям (34), (36), (37б) через моменты 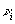 , , 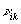 , , 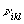 и и 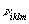 распределения интенсивности в объектной волне по волновым векторам распределения интенсивности в объектной волне по волновым векторам 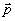 в плоскости х,у. в плоскости х,у.
ЧАСТЬ II
РАСЧЕТ ДИФРАКЦИОННОЙ ЭФФЕКТИВНОСТИ ГОЛОГРАММЫ
И ИСКАЖЕНИЙ ВОССТАНОВЛЕННОГО ПОЛЯ
Предположим, что записывающее поле состоит из опорной и объектной волн, каждая из которых характеризуется некоторым единым * ортом поляризации (в пренебрежении поляризационными исажениями):
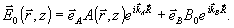 (38) (38)
Для определенности ми рассматриваем случай плоской опорной волны. Здесь 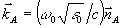 ; ; 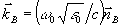 ; ; 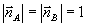 . Это поле создает в экспонированной голограмме возмущение диэлектрической проницаемости вида (9). В процессе восстановления перерассеяние из волны В в волну А и обратно естественным образом выделяет две пары ортов поляризации этих волн /16/.Одна из них соответствует так называемой s - поляризации, для которой . Это поле создает в экспонированной голограмме возмущение диэлектрической проницаемости вида (9). В процессе восстановления перерассеяние из волны В в волну А и обратно естественным образом выделяет две пары ортов поляризации этих волн /16/.Одна из них соответствует так называемой s - поляризации, для которой 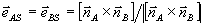 ; другая пара ортов (р - поляризация) имеет вид ; другая пара ортов (р - поляризация) имеет вид
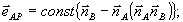 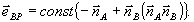
Орты р -пары лежат в плоскости векторов 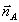 , , 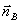 , а общий орт s - поляризации перпендикулярен этой плоскости. Мы будем считать, что в процессе восстановления подается опорная волна какого-то определенного (из двух упомянутых выше) типа поляризации; в силу линейности уравнений результат для произвольной поляризации может быть получен простой суперпозицией решений для собственных типов. Заметим, что на орты , а общий орт s - поляризации перпендикулярен этой плоскости. Мы будем считать, что в процессе восстановления подается опорная волна какого-то определенного (из двух упомянутых выше) типа поляризации; в силу линейности уравнений результат для произвольной поляризации может быть получен простой суперпозицией решений для собственных типов. Заметим, что на орты 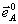 и и 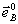 при записи никаких ограничений не накладывается. при записи никаких ограничений не накладывается.
В соответствии с идеологией модовой теории связанных пространственно-неоднородных волн поле на частоте 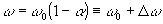
в процессе восстановления мы будем искать в виде структур, согласованных с возмущениями 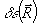 , имевшимися в обработанной голограмме, а именно, , имевшимися в обработанной голограмме, а именно,
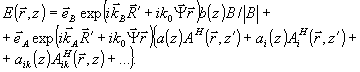 (39) (39)
Сватаемое 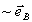 мы будем называть опорной волной при восстановлении, а члены мы будем называть опорной волной при восстановлении, а члены 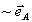 - восстанавливаемым объектным полем (вообще говоря, с искажениями). - восстанавливаемым объектным полем (вообще говоря, с искажениями).
Разложение объектного поля при восстановлении по нормированным производным возрастающих порядков от объектной волны 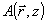 является, как будет видно из дальнейшего, разложением по степеням малого параметра является, как будет видно из дальнейшего, разложением по степеням малого параметра 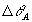 ; конкретнее ; конкретнее 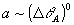 ; ; 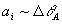 ; ; 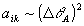 и т.д. Поэтому для не слишком малых значений "центрального угла падения" θА объектной волны в дальнейшем достаточно будет ограничиться учетом .вишь слагаемых ~aA+aiAi. В случае же параксиального падения объектной волны, т.е. при θА<ΔθА и т.д. Поэтому для не слишком малых значений "центрального угла падения" θА объектной волны в дальнейшем достаточно будет ограничиться учетом .вишь слагаемых ~aA+aiAi. В случае же параксиального падения объектной волны, т.е. при θА<ΔθА ( для описания искажений приходится учитывать также и слагаемые ~aikAik.
Подстановка поля (39) в правую часть уравнения (12) дает слагаемые различного вида. Среди них есть слагаемые, в которые быстрая экспонента очень сильно не удовлетворяет волновому уравнению, например, члены вида 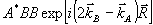 . В теории связанных волн такие члены отбрасываются с самого начала, поскольку они не возбуждают распространяющихся полей. . В теории связанных волн такие члены отбрасываются с самого начала, поскольку они не возбуждают распространяющихся полей.
Имеются слагаемые с быстрой зависимостью 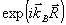 соответотвующей опорной волне. Они получаются в результате рассеяния самого опорного поля на интрамодуляционных возмущениях соответотвующей опорной волне. Они получаются в результате рассеяния самого опорного поля на интрамодуляционных возмущениях 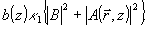 . .
В рамках модовой теории в этом выражении следует произвести замену 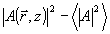 . Это означает, что опорная волна . Это означает, что опорная волна
"чувствует" среднюю по пространству засветку от объектного поля. Кроме того, в опорную волну на кросс-решетках вида 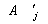 перерассеивается объектное поле: перерассеивается объектное поле: 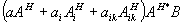 . .
Алгоритм модовой теории соответствует /6,8,10,16/ замене в этом выражении
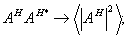 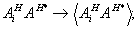 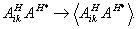 (40а)
Именно здесь проявляется удобство разложения по ортогональным функциям, поскольку 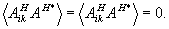 . .
Наконец, в правой части (12) возникают слагаемые с быстрой экспонентой, отвечающей объектному полю, 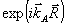 . Здесь прежде всего имеется рассеяние из опорного поля θ в объектную волну . Здесь прежде всего имеется рассеяние из опорного поля θ в объектную волну 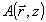 . Точнее говоря, применение оператора rot rot к выражению . Точнее говоря, применение оператора rot rot к выражению 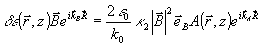 , во-первых, слагаемые , во-первых, слагаемые 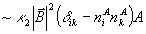 (двукратное дифференцирование экспоненты), и в результате генерируется неискаженная объектная волна (двукратное дифференцирование экспоненты), и в результате генерируется неискаженная объектная волна 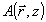 . Во-вторых, для р - поляризации будут возникать дополнительные слагаемые от однократного дифференцирования сравнительно медленной функции . Во-вторых, для р - поляризации будут возникать дополнительные слагаемые от однократного дифференцирования сравнительно медленной функции 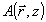 . Эти слагаемые . Эти слагаемые 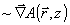 отвечают специфическим поляризационным искажениям, упоминавшимся в разделе 3 и появляющимся уже в борновском приближении. В соответствии со сказанным, там мы не будем их учитывать, имея в виду, что искажения, обусловленные усадкой, спектральным и угловым сдвигом и т.п. имеют заметно большую величину. Кроме того, имеется преломление объектной волны в присутствии однородного изменения диэлектрической проницаемости отвечают специфическим поляризационным искажениям, упоминавшимся в разделе 3 и появляющимся уже в борновском приближении. В соответствии со сказанным, там мы не будем их учитывать, имея в виду, что искажения, обусловленные усадкой, спектральным и угловым сдвигом и т.п. имеют заметно большую величину. Кроме того, имеется преломление объектной волны в присутствии однородного изменения диэлектрической проницаемости 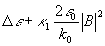 . Наконец, имеется перерассеяние объктной волны на "своей" интрамодулядионной решетке . Наконец, имеется перерассеяние объктной волны на "своей" интрамодулядионной решетке 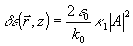 . Наиболее существенный момент модовой теории состоят в том, что эти слагаемые обрабатываются по следующему алгоритму: . Наиболее существенный момент модовой теории состоят в том, что эти слагаемые обрабатываются по следующему алгоритму:
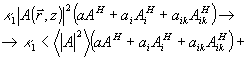 (40б)
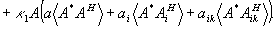
И здесь сказывается удобство работы с ортогонализованными функциями, так что это выражение переходит в
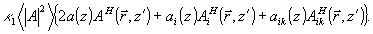 (40в)
Таким образом, неискаженная часть 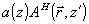 объектной волны чувствует "свою" интрарешетку с удвоенным коэффициентом. Именно эта двойка отличает медовую теорию связанных пространственно-неоднородных волн (т.е. волн со сложной спекл-структурой, кодированных) от теории Когельняка /4/ для пары плоских связанных волн. объектной волны чувствует "свою" интрарешетку с удвоенным коэффициентом. Именно эта двойка отличает медовую теорию связанных пространственно-неоднородных волн (т.е. волн со сложной спекл-структурой, кодированных) от теории Когельняка /4/ для пары плоских связанных волн.
С учетом всего сказанного мы должны подставить поле вида (39) в (12), обработать правую часть по указанному алгоритму и приравнять коэффициенты при 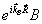 , , 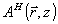 , , 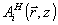 , , 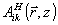 . В результате система уравнений для связанных волн приобретает вид . В результате система уравнений для связанных волн приобретает вид
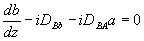 , (41а)
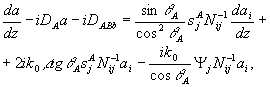 (41б)
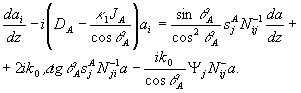 (41в)
Здесь мы считаем угол θA не слишком малым и поэтому ограничились учетом лишь слагаемых ~aA+aiAi. Кроме того, центральное направление 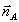 выбрано так, чтобы выбрано так, чтобы 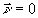 . В формулах (41) мы используем следующие обозначения (совпадающие, в основном, с введенными в /16/): . В формулах (41) мы используем следующие обозначения (совпадающие, в основном, с введенными в /16/):
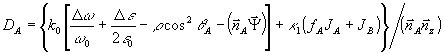 , (42а)
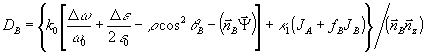 , (42б)
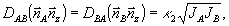 (42б)
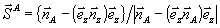 . (43) . (43)
Единичный вектор 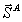 характеризует проекцию волнового вектора характеризует проекцию волнового вектора 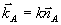 на плоскость поверхности голограммы. Кроме того, в этом разделе мы рассматриваем плоскую опорную и кодированную объектную волну, и поэтому в выражениях (42) следует, в соответствии с (7), положить fa=2, fB=1. Тем не менее, мы приводим выражения для DA и DB в виде (42 а,б) с тем, чтобы ниже в разделе 6 в пренебрежении искажениями рассмотреть также и случаи кодированной опорной волны и (или) плоской объектной волны. на плоскость поверхности голограммы. Кроме того, в этом разделе мы рассматриваем плоскую опорную и кодированную объектную волну, и поэтому в выражениях (42) следует, в соответствии с (7), положить fa=2, fB=1. Тем не менее, мы приводим выражения для DA и DB в виде (42 а,б) с тем, чтобы ниже в разделе 6 в пренебрежении искажениями рассмотреть также и случаи кодированной опорной волны и (или) плоской объектной волны.
Для параксиального падения объектной волны, θА<ΔθА, необходимо учитывать также и слагаемые ~aikAik. В этих условиях центральное значение 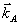 можно принять направленным точно по нормали к голограмме, θА=0; при этом небольшой реальный наклон объектного поля проявится в том, что можно принять направленным точно по нормали к голограмме, θА=0; при этом небольшой реальный наклон объектного поля проявится в том, что 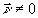 . .
В результате система уравнений дяя связанных волн принимает вид:
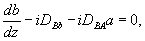 (44а)
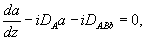 (44б)
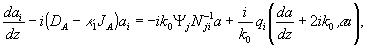 (44в)
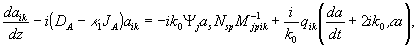 (44г)
где
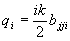 ; ; 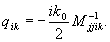 (45а)
При этом в выражениях (42а-в) нужно положить θА =0.
Системы (41) или (44) обладают рядом свойств, вытекающих из ортогональности и нормированности набора функций В, АН .
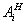 , , 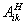 , ,
по которым производится рааяовение поля. Так, выражение для z - компоненты вектора Пойнтинта, усредненной по поперечным координатам, с точностью до членов ~ν' имеет вид:
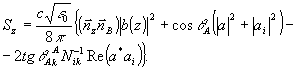 (46) (46)
Нетрудно проверить, что при вещественных ε 0, Δε, κ1 и κ2 (чисто фазовые голограммы без поглощения) из системы (41) следует точное соотношение:
dSz/dz=0, (47)
выражающее собой закон сохранения энергии. Выражение для вектора Пойнтинга с учетом слагаемых ~|aik|2 более сложно, и мы его здесь не приводам.
Граничные условия (13) в терминах амплитуд b, a, ai, aik примут следующий вид. Просветные голограммы:
b(z=0)=1, a(z=0)=ai(z=0)=aik(z=0)=0, (48a)
отражательные голограммы:
b(z=L)=1, a(z=0)=ai(z=0)=aik(z=0)=0. ( 48б)
Нулевое приближение модовой теории. Расчет дифракционной эффективности и селективностей.
Представление для. поля (39) и системы уравнений (41) или (44) основаны на разложении по степеням малого параметра ΔθА. В этой связи представляется естественным и решать эти системы методом последовательных приблинений. В нулевом приближении мы вообще пренебрегаем искажениями, т.е. слагаемыми ~аi и aik. При этом остается система уравнений для двух связанных амплитуд а(z) и b(z).
С учетом поглощения при записи коэффициенты DA, DB, DAB в этих уравнениях зависят от z, и тогда решение этой системы мояно получить лишь численно*. Подчеркнем, однако, что даже в этом случае речь идет не о численном решении исходного уравнения (12) в частных производных для полей со спекл-структурой, а лишь о решении системы двух обыкновенных дифференциальных уравнений. Это обстоятельство и состаляет основное достижение современной модовой теории связанных волн. Рассмотрение теории связанных плоских волн с учетом поглощения при записи проведено в работах /22,23/.
Мы ограничимся здесь случаем малого поглощения при записи, когда z –зависимостью величин JA, JB тем самым, коэффициентов DA, DB, DAB можно пренебречь. Тогда уравнения (41) имеют чисто экспоненциальные решения ~exp(μz) (моды, впервые введенные в работе /6/). Для просветных голограмм линейная комбинация этих решений, удовлетворяющая граничным условиям (48а), имеет вид (см./16/):
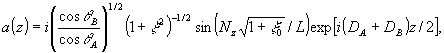 (49) (49)
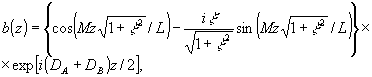
где введены обозначения
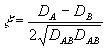 ; ; 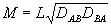 . (50) . (50)
В общем случае параметры ξ и М комплексны; они становятся вещественными лишь для чисто фазовых голограмм. Параметр М характеризует "силу голограммы", а параметр ξ - отстройку от точного выполнения условия Брэгга для перерассеяния из волны В в волну А . Дифракционную эффективность просветной ОГ ηпросв. мы определим как отношение z-компоненты вектора Умова-Пойнтинга 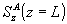 в восстановленной объектной волне на выходе к z-компоненте вектора Умова-Пойнтинга в восстановленной объектной волне на выходе к z-компоненте вектора Умова-Пойнтинга 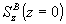 в опорной волне на входе. Тогда из (49), (50) следует /16/ в опорной волне на входе. Тогда из (49), (50) следует /16/
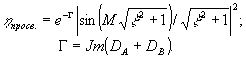 (51) (51)
Аналогично, для отражательной ОГ решение системы (41) в пренебрежении слагаемыми ~ai, и aik имеет вид:
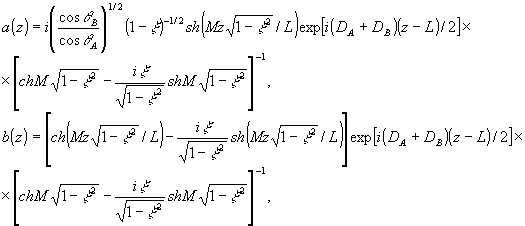 (52) (52)
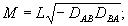 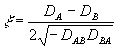 (53) (53)
и дифракционная эффективность ηотр. равна
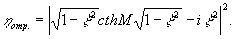 (54) (54)
Детальное исследование спектральной и угловой селективности (т.е. зависимости η от Δω, 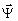 ), эффектов усадки, поляризаций и т.п. на основе выражений (49)-(54) проведено в работе /16/. Для нашего рассмотрения достаточна лишь следующие выводы, полученные в /16/. Дифракционная эффективность η~1 достигается при значениях силы голограммы |ξ|>1 и параметре отстройки |ξ|<1 уход в область |ξ|>1 приводит к довольно быстрому спаданию дифракционной эффективности. Поэтому ниже при вычислении искажений ~|aik|2, |aik|2 мы будем интересоваться лишь той областью значений величин Δε, δω/ω0 ), эффектов усадки, поляризаций и т.п. на основе выражений (49)-(54) проведено в работе /16/. Для нашего рассмотрения достаточна лишь следующие выводы, полученные в /16/. Дифракционная эффективность η~1 достигается при значениях силы голограммы |ξ|>1 и параметре отстройки |ξ|<1 уход в область |ξ|>1 приводит к довольно быстрому спаданию дифракционной эффективности. Поэтому ниже при вычислении искажений ~|aik|2, |aik|2 мы будем интересоваться лишь той областью значений величин Δε, δω/ω0, 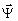 , ρ, JA, JB. Для которых дифракционная эффективность не слишком мала, т.е. |M|~1, |ξ|<1.
Расчет искажений в вос cтановленном объектном поле
Случай наклонного падения объетной волны
Дня нахождения искажений в восстанавливаемом объектом поле нужно вычислить поправки вида 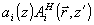 , , 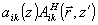 . В первом неисчезающем приближении по параметру ΔθА достаточно учесть лишь слагаемые ~aiAi. В силу ортогональности полей . В первом неисчезающем приближении по параметру ΔθА достаточно учесть лишь слагаемые ~aiAi. В силу ортогональности полей 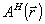 и и 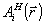 энергия, переносимая искаженной частью поля энергия, переносимая искаженной частью поля 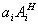 будет квадратичной по амплитуде ai; т.е. энергия искажении ~ будет квадратичной по амплитуде ai; т.е. энергия искажении ~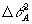 . Для нахождения ai(z) в . Для нахождения ai(z) в
первом неисчезавющем приближении достаточно в уравнении (41в) в качестве a(z) и b(z) подставить решения (49) и (52), соответствующие нулевому приближению, т.е. стандартной теории связанных неискаженных волн /16/. С учетом граничных условий ai(z=0)=0 получаем:
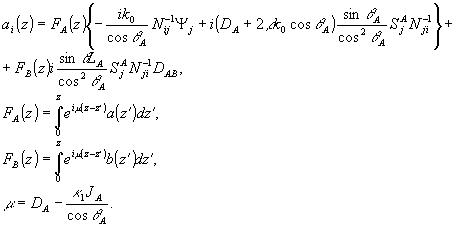 (55) (55)
Доля энергии, идущей в искажении объектной волны, составляет
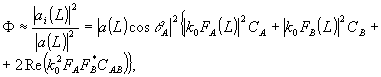 (56) (56)
Поскольку a(z) - безразмерно, FA и FB имеют размерность длины, то параметры СA, C B, СAB безразмерны:
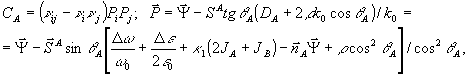 (57) (57)
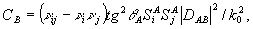 (58) (58)
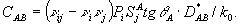 (59) (59)
Параметр μ характеризует поправку к z-компоненте волнового вектора свободно распространяющейся волны 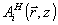 . Ее отличие от аналогичной поправки DA для волны . Ее отличие от аналогичной поправки DA для волны 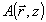 состоит в том, что последняя чувствует "свои" интрамодуляционные возмущения состоит в том, что последняя чувствует "свои" интрамодуляционные возмущения 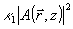 с гауссовсксй двойной, а волна, с гауссовсксй двойной, а волна, 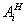 будучи ортогональной к будучи ортогональной к 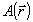 , чувствует эти возмущения просто по среднему уровню; поэтому μ-DA=-κ1 , чувствует эти возмущения просто по среднему уровню; поэтому μ-DA=-κ1J A/cosθA. Благодаря тому, что невозмущенные функции а(z) и b(z) суть линейные комбинации двух экспонент exp(μiz) , интегралы для FA(z) и FB(z) в (55) могут быть вычислены явно.
Обсудим вначале вклад каждого из слагаемых FA(L) и FB(L) в отдельности. Рассмотрим, например, слагаемое FB(L) для случая фазовых голограмм (просветных или страдательных) с малой дифракционной эффективностью. В этом случае работает борновокое приближение, и во всем объеме голограммы b(z)≈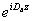 . Тогда . Тогда
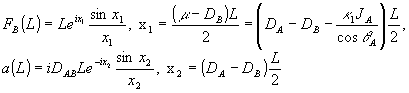 (60) (60)
Пусть , к тому же 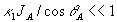 . Тогда х1≈х2 и вклад слагаемого |FB|2 в долю искажений равен . Тогда х1≈х2 и вклад слагаемого |FB|2 в долю искажений равен
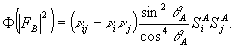 (61) (61)
Нетрудно видеть, что эта доля искажений совпадает с вычисленной ранее (22) для борновского приближения; однако здесь результат получен при произвольном несовпадении условий восстановления и записи, т.е. при Δω≠0, 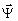 ≠0, ρ≠0, Δω≠0, θ, тем самым, при ξ≠0. Однако даже в борновском приближении максимальная дифракционная эффективность достигается при ξ=0, т.е. при DA-DB=0. В этом случае вклад слагаемого |FA|2 в долю искажений равен ≠0, ρ≠0, Δω≠0, θ, тем самым, при ξ≠0. Однако даже в борновском приближении максимальная дифракционная эффективность достигается при ξ=0, т.е. при DA-DB=0. В этом случае вклад слагаемого |FA|2 в долю искажений равен
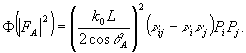 (62) (62)
Таким образом, слагаемое 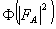 целиком обусловлено несовпадением параметров записи и восстановления ρ, целиком обусловлено несовпадением параметров записи и восстановления ρ, 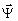 , Δω, Δε. Эти параметры для чисто фазовых голограмм можно подобрать так, чтобы они компенсировали друг друга в выражении для ξ давая ξ≈0. Такой подбор соответствует выполнению условия Брэгга для рассеяния В→А, но лишь для "центральных" волновых векторов , Δω, Δε. Эти параметры для чисто фазовых голограмм можно подобрать так, чтобы они компенсировали друг друга в выражении для ξ давая ξ≈0. Такой подбор соответствует выполнению условия Брэгга для рассеяния В→А, но лишь для "центральных" волновых векторов 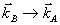 . Из-за того, что поле . Из-за того, что поле 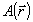 обладает протяженным угловом спектром, условие Брэгга перестает выполняться для "боковых" компонент обладает протяженным угловом спектром, условие Брэгга перестает выполняться для "боковых" компонент 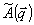 , что и приводит к искажениям рассматриваемого типа. Конкретно это обусловлено тем, что в параметр , что и приводит к искажениям рассматриваемого типа. Конкретно это обусловлено тем, что в параметр 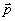 из (59) величины ρ, Δε, Δω, из (59) величины ρ, Δε, Δω, 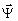 входят в другой комбинации, нежели в параметр входят в другой комбинации, нежели в параметр 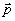 , определяющий дифракционную эффективность. , определяющий дифракционную эффективность.
На первый взгляд, искажения типа 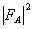 пропорциональны однородному многочлену 2-й степени по малым параметрам пропорциональны однородному многочлену 2-й степени по малым параметрам 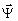 , Δω, ρ, Δε, β отличие от слагаемых ~|FB|2, которые такой малости не содержат. Однако в слагаемых |FA|2 содержится большой параметр (k0L/2)2. Так, для n = 1,3, λ = 0,5 мкм, L = 10 мкм имеем (k0L/2)≈4∙103. Из-за этого даже сравнительно умеренные значения Δω, , Δω, ρ, Δε, β отличие от слагаемых ~|FB|2, которые такой малости не содержат. Однако в слагаемых |FA|2 содержится большой параметр (k0L/2)2. Так, для n = 1,3, λ = 0,5 мкм, L = 10 мкм имеем (k0L/2)≈4∙103. Из-за этого даже сравнительно умеренные значения Δω, 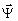 , ρ, Δε μогут приводить к весьма сильным искажениям, гораздо большим, чем искажения (58) борновского типа. Поэтому здесь и в дальнейшем искажения борновского типа, а также совпадающие с ними по порядку величины поляризационные искажения для р - поляризаций мы не будем рассматривать, и сосредоточимся лишь на искажениях, генерируемых за счет , ρ, Δε μогут приводить к весьма сильным искажениям, гораздо большим, чем искажения (58) борновского типа. Поэтому здесь и в дальнейшем искажения борновского типа, а также совпадающие с ними по порядку величины поляризационные искажения для р - поляризаций мы не будем рассматривать, и сосредоточимся лишь на искажениях, генерируемых за счет 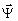 , Δω, Δε, ρ. Μы не будем также учитывать и интерференционные слагаемые , Δω, Δε, ρ. Μы не будем также учитывать и интерференционные слагаемые 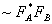 . .
Рассмотрим теперь другой предельный случай - фазовую голограмму с большой дифракционной эффективностью, для определенности отражательную. При этом, опять-таки, мы ограничимся задачей ξ=0, что обеспечивает максимальность дифракционной эффективности η=thM≈1 при М>2,5. Тогда интегрирование в (55) дает
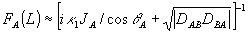 (63) (63)
Для случая, когда 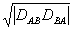 > >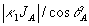 , выражение (56) для доли искажений принимает вид , выражение (56) для доли искажений принимает вид
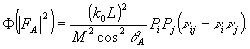 (64) (64)
Таким образом, и здесь интенсивность искажений содержит очень большой параметр (k0L)2. Нетрудно понять, что при достаточно больших искажениях, т.е. когда Ф из (56) становится сравнимым с единицей, может потребоваться учет обратного влияния возмущений 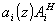 на волну a(z)А. В этом случае нужно решать полную систему связанных уравнений для a и ai (в неборновском случае - еще и для b(z)). Для частного случая параксиальной задачи θA на волну a(z)А. В этом случае нужно решать полную систему связанных уравнений для a и ai (в неборновском случае - еще и для b(z)). Для частного случая параксиальной задачи θA, θB << 1 об искажениях из-за спектрального сдвига и Δω такого рода обратное влияние было рассмотрено в работе /10/ на языке мод.
Обсудим теперь структуру восстановленного (с искажениями) поля объектной волны:
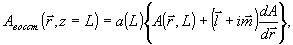 (65) (65)
где вещественные двумерные векторы li и mi в основном пропорциональны мнимой и вещественной части отношения ai(L)/a(L):
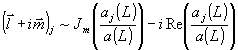 . (66) . (66)
Случай, когда отношение aj/а есть вещественный вектор, т.е. 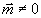 , , 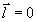 , был обсужден в разделе 3. Эти искажения соответствуют разной по модулю амплитуде восстановления разных угловых компонент и аналогичны искажениям за счет угловой зависимости коэффициента френелевского отражения при наклонном падении. , был обсужден в разделе 3. Эти искажения соответствуют разной по модулю амплитуде восстановления разных угловых компонент и аналогичны искажениям за счет угловой зависимости коэффициента френелевского отражения при наклонном падении.
В отличие от этого, случай с чисто мнимым ai/а отвечает 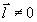 , , 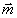 =0, и тогда c той же точностью =0, и тогда c той же точностью
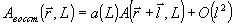 . (67) . (67)
Иначе говоря, искажения этого типа соответствуют смещению объектной волны по поперечной координате на вектор 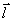 . Нетрудно проверить, что доля искажений становится порядка 1 в том . Нетрудно проверить, что доля искажений становится порядка 1 в том
случае, когда величина смещения 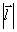 становится порядка поперечного размера становится порядка поперечного размера 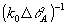 спекл-структуры поля спекл-структуры поля 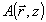 . .
Параксиальное падение объектной волны
Случай параксиального падения объектной волны требует учета слагаемых ~aikAik в дополнение к слагаемым вида аА и aiAi. Это связано с тем, что целый ряд членов в ai(z) содержит множитель sinθA, и поэтому при θA→0 они становятся сравнимыми с aik. В соответствии со сказанным в разделе 5 для параксиального падения объектной волны мы примем θA=0 , а реально имеющийся небольшой наклон центрального направления объектной волны проявится в том, что 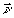 ≠0. ≠0.
Как и в случае наклонного падения, величины ai(z) и aik(z) мы найдем методом последовательных приближений, используя невозмущенные функции а(z) и b(z). Это дает
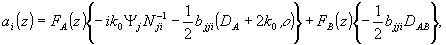 (68a) (68a)
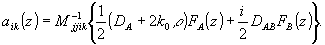 (68б)
При этом функции FA(z) и FB(z) могут быть взяты из (55) при θA=0, и в выражении для aik мы опустили слагаемые ~Ψ2. Доля энергии, содержащаяся в искажениях, может быть определена теперь как
Ф=(|ai|2+|aik|2)/|a|2. (69a)
Выпишем здесь лишь наиболее существенные слагаемые (ср.с обсуждением выше в разделе 7а):
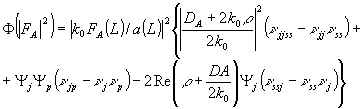 ( ( 69б)
Отметим, что в частном случае прооветных фазовых голограмет при ρ =0, 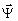 = 0, Δε=0, Δω≠0 и в пренебрежении слагаемыми κ1 = 0, Δε=0, Δω≠0 и в пренебрежении слагаемыми κ1(2J A+J B) в выражении для DA формула (69б) совпадает с выражением, впервые полученным в /10/.
Выражение (69б) показывает, что и для параксиального случая интенсивность искажений, обусловленных несовпадением условий записи и восстановления, содержит большой параметр |k0FA/a|2~(k0L)2. При этом угловой фактор составляет величину, пропорциональную (ΔθА)4 для возмущений ~(Δω/ω)2, ρ2, Δε2 и пропорциональную (ΔεA) 2 для возмущений ~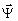 . .
Фигурирующий выше тензор νij-νiνj удобно выразить через угловые параметры объектной волны в воздухе. Пусть показатель преломления материала голограммы равен n, центральное направление объектной волны составляет угол θвозд с осью z (угол падения в воздухе). Пусть, кроме того, средний квадрат расходимости пучка в воздухе составляет <(Δαxz) 2> в плоскости падения и <(Δαy) 2> в перпендикулярном направлении (все для воздуха). Тогда из законов преломления следует
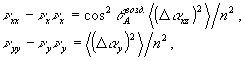 (70) (70)
при этом вектор 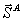 совпадает с ортом совпадает с ортом 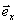 . .
Заключение
Приведем некоторые численные оценки. Рассмотрим отражательную фазовую голограмму с большой дифракционной эффективностью. Пусть М=25, η=th2M≈0,97 и θАвозд=45°, 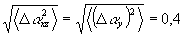 рад ≈23°. Рассмотрим влияние усадки ρ≈0,045. Пусть, как при записи, так и при восстановлении опорная волна идет точно вдоль оси z, т.е. θВ=0; в этом случае Δε=0. Κроме того, примем, что Δε=0. Δля достижения максимальной дифракционной эффективности, ε=0, мы должны взять Δω/ω=ρcosθA (при этом мы считаем величину κ1JA рад ≈23°. Рассмотрим влияние усадки ρ≈0,045. Пусть, как при записи, так и при восстановлении опорная волна идет точно вдоль оси z, т.е. θВ=0; в этом случае Δε=0. Κроме того, примем, что Δε=0. Δля достижения максимальной дифракционной эффективности, ε=0, мы должны взять Δω/ω=ρcosθA (при этом мы считаем величину κ1JA
не слишком большой и пренебрегаем ее вкладом в 4 )• Вектор Р из (57) принимает значение
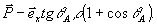
Подставляя этот вектор и (70) в (64), при λ=0,5 мкм, L=10 мкм для доли искажений получим, Ф≈50%. Это показывает, насколько велико влияние сравнительно умеренных отличий условий восстановления и записи на долю шумов.
Оценим теперь искажения при всех тех же условиях, но для параксиального случая. Мы примем 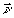 =0, νikl =0, νikl=0, νjjss= 8<Δαy2> 2n -4, νjjνss=4<(Δαy) 2> 2n -4; при этом мы считали форму углового распределения j(α) гауссовской, j(α)~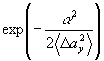 . Тогда из (69б) получим Ф≈20%. . Тогда из (69б) получим Ф≈20%.
Таким образом, в настоящей работе дан количественный анализ искажений поля при восстановлении кодированной объектной волны в объемной голограмме. Искажения обусловлены, главным образом, несовпадением условий восстановления и записи-усадкой, оптическим уплотнением, сдвигом угла и частоты опорной волны - и в общем случае достаточно велики. Найдены не только общая интенсивность искажений, но и их конкретный вид.
Общая интенсивность рассмотренных здесь искажений растет с ростом угловой ширины ΔθА объектного поля. С другой стороны, в работе /19/ были количественно определены интрамодуляционные ("змеечные") искажения волны, восстановленной в ОГ; они уменьшаются как ΔθА-2. Наличие количественных выражений для искажений обоих типов позволяет поставить задачу об оптимальном выборе угловой ширины ΔθА, минимизирующей полные искажения.
Л и т е р а т у р а
1. D.Gabor. Nature, 161, 777, 1948.
2. E.N.Leith, J.Upatnieks. JOSA, 52, 1123, 1962.
3. Ю.Н.Денисюк. ДАН СССР, 144,1275(1962).
4. H.Kogelnik. Bell.Syst.Techn.Journ., 48, 2909, 1969.
5. D.J.Cooke, L.Solymar, C.J.Sheppard. Int.J.Electron, 46, 337, 1979.
6. В.Г.Сидорович. ЖТФ, 46, 1306(1976).
7. В.В.Аристов. В.Ш.Шехтман. УФН, 104, 51, 1971.
8. В.Г.Сидорович, ЖТФ, 46, 2168, 1976; И.М.Бельдюгин, М.Г.Галушкин, Е.М.Земсков, В.И.Мандросов, Квант.электр., 3, 2467,1976.
9. Б.Я.Зельдович, В.И.Поповичев, В.В.Рагульский, Ф.С.Файзуллов. Письма в ЖЭТФ, 15, 160, 1972.
10. В.Г.Сидорович, В.В.Шкунов. Оптика и спектр., 44, 1001, 1978.
11. Ш.Д.Какичашвили. Оптика и спектр., 42, 390, 1977.
12. V.V.Shkunov, B.Ya.Zeldovich. Appl.Opt., 18, 3633, 1979.
13. Б.Я.Зельдович, В.В.Шкунов. Препринт ФИАН № 266, 1978.
14. Б.Я.Зельдович, В.В.Шкунов. Квант.электр., 6, 1533, 1979.
15. А.А.Лещев. В.Г.Сидорович. В сб."Оптическая голография", "Наука", Л., стр.42, 1978.
16. Б.Я.Зельдович, В.В.Шкунов, Т.В.Яковлева. Препринт ФИАН № 54, 1979.
17. Б.Я.Зельдович, В.В.Шкунов. Материалы Х Всесоюзной школы по голографии, т.2, стр.46-84, Ленинград, 1978.
18. В.Г.Сидорович. Материалы Х Всесоюзной школы по голографии, т.1, стр.1 61-186, Ленинград, 1978.
19. Б.Я.Зельдович, В.В.Шкунов, Т. В. Яковлева. Преприит ФИАН № 26, 1979.
20. Б.Я.Зельдович, Т.В.Яковлева. Квант.электр., 7, 519, 1980.
21. М.Борн, Э.Вольф. Основы оптики, "Наука", М., 1973.
22. Б.Я.Зельдович, В.В.Шкунов. Краткое сообщение физ.ФИАН. № 1, стр.24, 1979.
23. F.Lederer, U.Laugbein. Opt.Quant.Electron, 9, 473, 1977.
S.Horozumi. Jap.Journ .Appl.Рhуs., 47, 190, 1976.
R.Kowarschik. Opt.Acta, 23, 1039, 1976.
T.Kubota. Opt.Acta, 25, 1035, 1978.
И.К.Любавская , О.Б. Серов, А.Н.Смолович. Письма ЖТФ, 6, 38, 1980.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

