|
|
 |
 |

|
| |
МЕТОД ФАЗОВОГО СОПРЯЖЕНИЯ В УСЛОВИЯХ НЕЛИНЕЙНОЙ РЕФРАКЦИИ СВЕТОВЫХ ПУЧКОВ
М.А.Воронцов
Исследуется эффективность работы фазосопряженной адаптивной оптической системы фокусировки излучения в нелинейной неоднородной среде. Сформулирован обобщенный принцип оптической обратимости. Показано, что алгоритм фазового сопряжения приводит к оптимизации некоторого квадратичного функционала методом условного градиента. Использование алгоритма в адаптивных оптических системах при работе по объектам с неточечной структурой рассеивающей поверхности, не позволяет достичь дифракционно ограниченной фокусировки излучения.
В адаптивных оптических системах фокусировки излучения фазовый профиль посланного светового пучка формируется управляющим устройством по некоторому алгоритму. Один из наиболее распространенных методов коррекции начального фазового фронта - алгоритм фазового сопряжения - основан на предположении об оптической обратимости. Согласно этому предположению, фазовые искажения пучка при его распространении в неоднородной линейной среде аддитивно суммируются и тем самым их влияние эквивалентной действию некоторой тонкой линзы, которое можно скомпенсировать, внося в фазу излученной волны некоторое предыскажение. В качестве корректирующего фазового профиля посланной волны используется взятая с обратным знаком фаза волны, рассеянной объектом /1/. Настоящая работа посвящена исследованию метода обращения волнового фронта в условиях нерегулярной, нелинейной среды, когда нет оптической обратимости.
Основные результаты работы сводятся к следующему.
1. Сформулирован обобщенный принцип оптической обратимости, справедливый в случае распространения световых пучков в нели-
нейной неоднородной среде.
2. В линейной неоднородной среде использование в адаптивной оптической системе метода фазового сопряжения приводит к оптимизации следующего функционала:
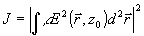 (1) (1)
методом условного градиента /2/. Здесь 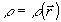 - комплексный коэффициент рассеяния излучения поверхностью объекта, расположенного в точке z=z0, E( - комплексный коэффициент рассеяния излучения поверхностью объекта, расположенного в точке z=z0, E(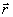 ,z) - комплексная амплитуда электрического поля посланной волны. ,z) - комплексная амплитуда электрического поля посланной волны.
3. Показано, что алгоритм обращения волнового фронта позволяет получить лишь приближенную фокусировку излучения, т.е. дифракционно-ограниченная фокусировка световых пучков на объекте недостижима даже в линейном случае.
Оптическую систему с обратной связью, предназначенную для передачи световой энергии на некоторое расстояние z0 в неоднородной нелинейной среде можно описать следующей системой уравнений для комплексных амплитуд излученной Е (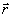 ,z) и рассеянной поверхностью объекта Ψ( ,z) и рассеянной поверхностью объекта Ψ(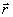 ,z) волн*/ ,z) волн*/:
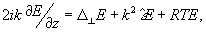 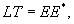 (2) (2)
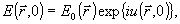 (3) (3)
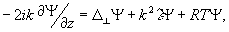 (4) (4)
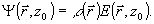 (5) (5)
Здесь K - волновое число, 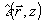 - флуктуации диэлектрической проницаемости вдоль по трассе, R - параметр нелинейности, L - некоторый дифференциальный оператор, описывающий взаимодействие световой волны со средой, - флуктуации диэлектрической проницаемости вдоль по трассе, R - параметр нелинейности, L - некоторый дифференциальный оператор, описывающий взаимодействие световой волны со средой, 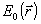 - амплитудный профиль посланной волны, - амплитудный профиль посланной волны, 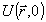 - начальный фазовый профиль, формируе- - начальный фазовый профиль, формируе-
мый оптической системой.
Умножим уравнение (2) на Ψ(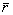 ,z), а уравнение (4) на Е( ,z), а уравнение (4) на Е(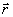 ,z) и проинтегрируем полученные выражения по ,z) и проинтегрируем полученные выражения по 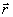 в бесконечных пределах. Далее, вычитая из первого соотношения второе, получим интегральное соотношение в бесконечных пределах. Далее, вычитая из первого соотношения второе, получим интегральное соотношение 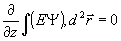 , из которого в силу (3), (5) следует , из которого в силу (3), (5) следует
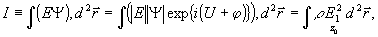 (6) (6)
где 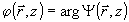 и и 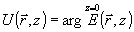 . Заметим, что подученное интегральное соотношение справедливо для нелинейной неоднородной среды, определяемой уравнениями (2), (4). . Заметим, что подученное интегральное соотношение справедливо для нелинейной неоднородной среды, определяемой уравнениями (2), (4).
Итерационный процесс последовательного обращения волнового фронта рассеянной волны Ψ(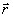 ,0) приводит к следующему алгоритму коррекции фазы: ,0) приводит к следующему алгоритму коррекции фазы:
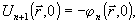 n=0,1,…, (7) n=0,1,…, (7)
через 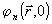 - обозначен фазовый профиль рассеянного поля, полученный при - обозначен фазовый профиль рассеянного поля, полученный при 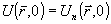 . Если алгоритм (7) сходится, то . Если алгоритм (7) сходится, то 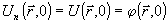 и для мнимой части (6) получим интегральное соотношение и для мнимой части (6) получим интегральное соотношение 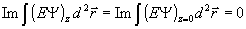 , из которого следует следующий обобщенный принцип оптической обратимости: , из которого следует следующий обобщенный принцип оптической обратимости:
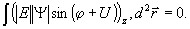 (8) (8)
Это условие содержит обычную формулировку принципа обратимости, справедливую в геометрическом приближении: 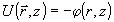 , но не эквивалентно ему. Согласно (8), в нелинейной неоднородной среде, с учетом дифракции, фазовые профили излученной и рассеянной объектом волн совпадают лишь в среднем. , но не эквивалентно ему. Согласно (8), в нелинейной неоднородной среде, с учетом дифракции, фазовые профили излученной и рассеянной объектом волн совпадают лишь в среднем.
Покажем, что в линейном случае ( R=0) итерационная процедура (7) коррекции фазы посланной волны оптимизирует критерий (1). Используя предложенную в /3/ методику оптимизации нелиней-
ных оптических систем для приращения функционала ΔJ можно записать следующее выражение:
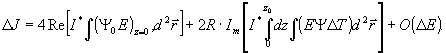 (9) (9)
Функция Ψ удовлетворяет уравнению (5), через O(ΔE) обозначены члены второго порядка малости по приращениям ΔЕ, ΔТ. Из (9) следует, что в линейной неоднородной среде по вариации начального профиля ΔЕ(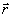 ,0) можно непосредственно судить о изменении критерия J, которое обусловлено этой вариацией. Тем самым, на основе анализа рассеянной волны в точке z=0 можно рассчитать градиент функционала 3 и воспользоваться для построения корректирующей последовательности Un( ,0) можно непосредственно судить о изменении критерия J, которое обусловлено этой вариацией. Тем самым, на основе анализа рассеянной волны в точке z=0 можно рассчитать градиент функционала 3 и воспользоваться для построения корректирующей последовательности Un(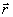 ,0) начальных фазовых профилей одним из градиентных методов /3/. Согласно методу условного градиента /3/ очередная корректирующая фаза определяется из условия max(ΔJ). Учитывая (6), легко показать, что максимум приращения ΔJ достигается при ,0) начальных фазовых профилей одним из градиентных методов /3/. Согласно методу условного градиента /3/ очередная корректирующая фаза определяется из условия max(ΔJ). Учитывая (6), легко показать, что максимум приращения ΔJ достигается при 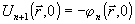 , что совпадает с алгоритмом фазового сопряжения (7). Таким образом, в линейном случае фазосопряженные оптические системы практически реализуют метод условного градиента и оптимизируют с помощью этого метода функционал J. В нелинейной среде приращение ΔJ в явной форме не выражается через приращение начального профиля и оптимизация обращением волнового фронта первого слагаемого в (9) не означает еще оптимизацию самого функционала ΔJ, что неизбежно приводит к снижению эффективности фазосопряженной коррекции в нелинейной среде. , что совпадает с алгоритмом фазового сопряжения (7). Таким образом, в линейном случае фазосопряженные оптические системы практически реализуют метод условного градиента и оптимизируют с помощью этого метода функционал J. В нелинейной среде приращение ΔJ в явной форме не выражается через приращение начального профиля и оптимизация обращением волнового фронта первого слагаемого в (9) не означает еще оптимизацию самого функционала ΔJ, что неизбежно приводит к снижению эффективности фазосопряженной коррекции в нелинейной среде.
Остановимся более подробно на физическом смысле функционала J. При наличии на объекте неразрешаемого пучком зеркального пятна площади S коэффициент рассеяния равен некоторой постоянной С≤1 внутри S и 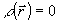 пятна. В этом случае максимальное значение J реализуется в том случае, когда фаза пучка в пределах S является плоской (среда предполагается однородной). Это соответствует приближенной фокусировке излучения (фокусировка в перетяжку). пятна. В этом случае максимальное значение J реализуется в том случае, когда фаза пучка в пределах S является плоской (среда предполагается однородной). Это соответствует приближенной фокусировке излучения (фокусировка в перетяжку).
Таким образом, при использовании алгоритма фазового сопряжения недостижим дифракционно ограниченный размер сфокусирован-
ного пятна даже в линейной однородной среде.
Если поверхность объекта имеет несколько блестящих точек, то 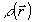 является многоэкстремальной функцией, что может привести к распределению энергии по максимумам является многоэкстремальной функцией, что может привести к распределению энергии по максимумам 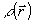 . В этом случае J не отражает качество процесса фокусировки и его оптимизация обращением волнового фронта не означает фокусировку излучения. . В этом случае J не отражает качество процесса фокусировки и его оптимизация обращением волнового фронта не означает фокусировку излучения.
Л и т е р а т у р а
1. Дж.У.Харди, ТИИЭР, 66, №6, 31, 1978.
2. Ф.П.Васильев. Лекции по методам решения экстремальных задач, М., изд.МГУ, 1974.
3. М.А.Воронцов. I Всесоюзная конференция "Проблемы управления параметрами лазерного излучения", тезисы докладов, ч. II, 157, Ташкент, 1978.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

