|
|
 |
 |

|
| |
КОГЕРЕНТНОСТЬ СУПЕРПОЗИЦИОННЫХ СОСТОЯНИИ АТОМОВ
ПРИ ФОРМИРОВАНИИ ТРАНЗИЕНТ-РЕШЕТОК
Е.И.Штырков
Обсуждаются особенности нового переходного квантового оптического явления: формирования пространственных индуцированных транзиент-решеток путем интерференции атомных суперпозипионных состояний.
1. Введение
Методы создания динамических светоиндуцированных решеток, формируемых в веществе при помещении его в место пересечения когерентных пучков света, вызывает все больший интерес из-за его перспективных свойств. Решетки используются для записи и восстановления волновых фронтов света /1/, измерения различных характеристик веществ (времен релаксации возбужденных энергетических состояний атомов, например, в рубине /2,3/ или в CdSxSe1-x /4/ вероятностей сверхбыстрых переходов /5/, коэффициентов амбиполярной диффузии неравновесных носителей, например, в кремнии /6/ и т.д.), для генерации звуковых волн /7/ в лазерах с распределенной обратной связью /8/ и т.п. (см.,например, обзор /9/).
Общим для всех предыдущих работ, изучающих динамические светоиндуцировсооше решетки, является то, что пучки когерентного света, формирующие решетку, действуют на среду одновременно, интерферируют и тем самым пространственно модулируют характеристики среды. Однако недавно /10/ была показана возможность создавать пространственные решетки в резонансной среде даже в случае, когда пучки света накачки не могут непосредственно интерферировать друг с другом, если они имеют импульсный характер и подаются на среду в разное время. Необходимым условием возбужде-
ния среды пучками света, разделенными во времени интервалом τ для этого является
δt<τ<T 2, (1)
где dt, Т2 - длительность импульсов накачки и время поперечной релаксации атомного перехода. Последнее, как известно, определяет скорость релаксации неравновесной поляризации среда и, следовательно, необратимую потерю фазовой "памяти" среды. При таким условии (1) во время действия второго импульса света накачки с волновым вектором 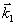 , направленным под некоторым углом к волновому вектору первого импульса , направленным под некоторым углом к волновому вектору первого импульса 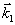 , как разность населенности, так и неравновесная поляризация на резонансно возбуждаемом энергетическом переходе пространственно модулируются в диде решеток /10/, с пространственным периодом , как разность населенности, так и неравновесная поляризация на резонансно возбуждаемом энергетическом переходе пространственно модулируются в диде решеток /10/, с пространственным периодом 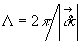 , где , где 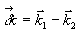 - вектор решетки. Эта решетка формируется вследствие интерференции атомных суперпозиционных состояний и только в том случае, когда к моменту прихода второго импульса еще не произошла существенная потеря фазовой "памяти" в системе, вызванная необратимыми процессами релаксации. Различные процессы релаксаций, которые определяют однородный характер уширения резонансного перехода, сбивают фазу колебаний отдельных частиц и поэтому нарушают когерентность колебаний в системе атомов. Другими словами, все процессы релаксации, разрушающие макроскопическую неравновесную поляризацию среды, определяют длительность фазовой памяти атомной системы. В случае длинной фазовой памяти индуцированные решетки, формируемые при условии (1), имеют глубину пространственной модуляции, пропорциональную ехр(-τ/Т2 - вектор решетки. Эта решетка формируется вследствие интерференции атомных суперпозиционных состояний и только в том случае, когда к моменту прихода второго импульса еще не произошла существенная потеря фазовой "памяти" в системе, вызванная необратимыми процессами релаксации. Различные процессы релаксаций, которые определяют однородный характер уширения резонансного перехода, сбивают фазу колебаний отдельных частиц и поэтому нарушают когерентность колебаний в системе атомов. Другими словами, все процессы релаксации, разрушающие макроскопическую неравновесную поляризацию среды, определяют длительность фазовой памяти атомной системы. В случае длинной фазовой памяти индуцированные решетки, формируемые при условии (1), имеют глубину пространственной модуляции, пропорциональную ехр(-τ/Т2). Это позволяет по величине дифракционной эффективности решетки непосредственно измерять время поперечной релаксации, а следовательно, ширину однородного уширения перехода, даже в случае его маскировки неоднородным уширением. Для пояснения этого обратимся к рис.1, где представлен случай атомной системы, в которой неоднородное уширение перехода преобладает (кривая 1). В этой системе произвольная группа атомов с частотой уширена однород-
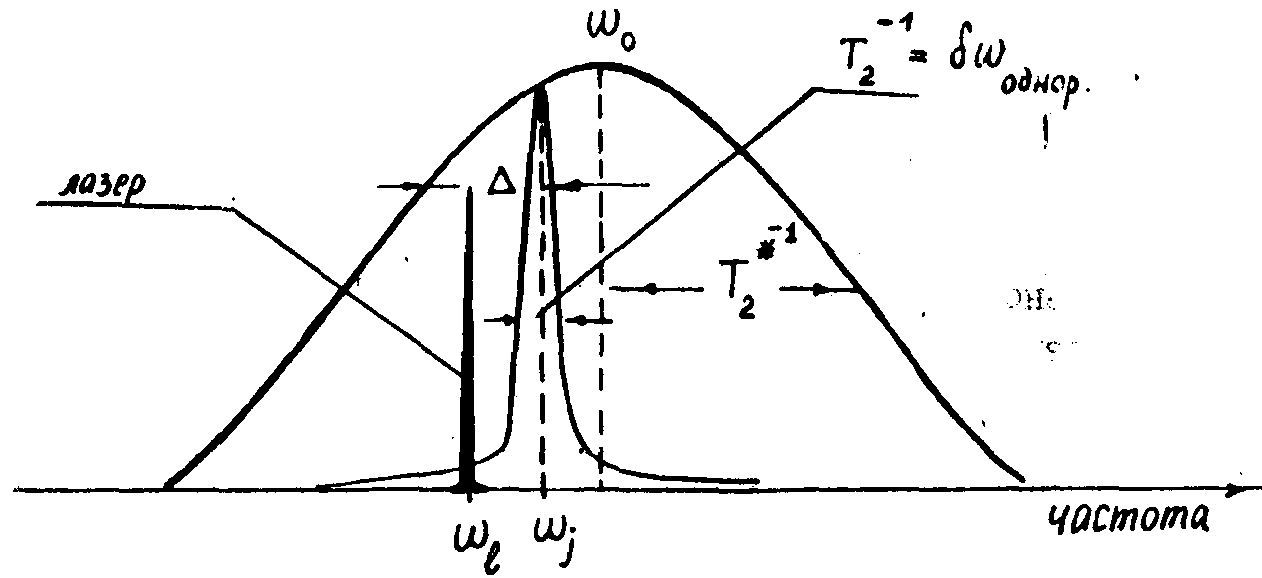
Рис.1. Спектральные линии поглощения и накачки.
ным образом (кривая 2). Ширина спектра однородного уширения равна 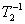 , т.е. для выполнения условия (1) необходимо либо выбирать необходимую систему с как можно более узкой линией однородного уширения (например, разреженные газы), либо подготавливать систему определенным образом (например, охлаждать кристалл до низких температур). Создание пространственной решетки при условии (1) является одним из ряда переходных оптических квантовых явлений типа фотон-эха, самоиндуцированной прозрачности, оптической нутации (так называемые транзиент-эффекты) и поэтому открывает новые возможности для изучения фундаментальных вопросов взаимодействия света с атомами. Явление формирования пространственной транзиент-решетки при условии (1) было вскоре экспериментально обнаружено /11/ в рубине на переходе , т.е. для выполнения условия (1) необходимо либо выбирать необходимую систему с как можно более узкой линией однородного уширения (например, разреженные газы), либо подготавливать систему определенным образом (например, охлаждать кристалл до низких температур). Создание пространственной решетки при условии (1) является одним из ряда переходных оптических квантовых явлений типа фотон-эха, самоиндуцированной прозрачности, оптической нутации (так называемые транзиент-эффекты) и поэтому открывает новые возможности для изучения фундаментальных вопросов взаимодействия света с атомами. Явление формирования пространственной транзиент-решетки при условии (1) было вскоре экспериментально обнаружено /11/ в рубине на переходе
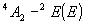
при низких температурах (2°К), достаточных для удлинения времени фазовой "памяти" до сотен наносекунд. Рассмотрим более подробно условия формирования индуцированных транзиент-решеток в общем случае, когда имеется произвольная частотная расстройка волны накачки от точного резонанса (случай точного резонанса рассмотрен в /10/). На рис.1 изображен такой случай. Поле накачки имеет форму последовательных импульсов линейно-
поляризованного монохроматического света :
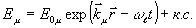 , (2) , (2)
где к.с. - комплексно-сопряженная величина, 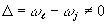 . Среда представляет собой двухуровневую невырожденную систему атомов с энергетическим расщеплением ħωj, где j - индекс характеризует группу атомов, соответствующую определенной изохромате неоднородно уширенного спектра поглощения. Рассмотрение системы в виде двухуровневых атомов вполне обосновано для оптических переходов. В настоящее время для изучения динамики двухуровневых атомов плодотворно применяют оптические уравнения типа Блоха для средних значений компонент энергетического спина . Среда представляет собой двухуровневую невырожденную систему атомов с энергетическим расщеплением ħωj, где j - индекс характеризует группу атомов, соответствующую определенной изохромате неоднородно уширенного спектра поглощения. Рассмотрение системы в виде двухуровневых атомов вполне обосновано для оптических переходов. В настоящее время для изучения динамики двухуровневых атомов плодотворно применяют оптические уравнения типа Блоха для средних значений компонент энергетического спина 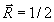 /12/, поскольку через эти компоненты можно выразить как разность населенности энергетических уровней атомного перехода, так и поляризацию среды. Уравнение движения для среднего значения энергетического спина имеет вид (см., например, /13/) /12/, поскольку через эти компоненты можно выразить как разность населенности энергетических уровней атомного перехода, так и поляризацию среды. Уравнение движения для среднего значения энергетического спина имеет вид (см., например, /13/)
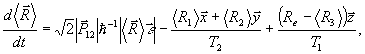 (3) (3)
где 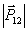 - модуль матричного элемента дипольного момента перехода; ħ = 1,06∙10-34 дж∙с; - модуль матричного элемента дипольного момента перехода; ħ = 1,06∙10-34 дж∙с; 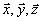 - орты по осям координат; - орты по осям координат; 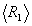 , , 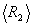 - средние значения поперечных компонент энергетического спина (предполагается, что свет направлен по ocи OZ); - средние значения поперечных компонент энергетического спина (предполагается, что свет направлен по ocи OZ); 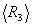 - среднее значение продольной компоненты энергетического спина, равновесное значение которой Rl до начала возбуждения для оптических переходов может быть положено N0j (j - концентрация частиц в Т1-й группе атомов); T1 - время продольной релаксации. Вектор ε связан с линейнополяризованными оптическими полями (2), предварительно разложенными на циркулярнополяризованные компоненты в форме - среднее значение продольной компоненты энергетического спина, равновесное значение которой Rl до начала возбуждения для оптических переходов может быть положено N0j (j - концентрация частиц в Т1-й группе атомов); T1 - время продольной релаксации. Вектор ε связан с линейнополяризованными оптическими полями (2), предварительно разложенными на циркулярнополяризованные компоненты в форме
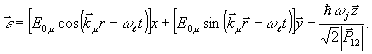 (4) (4)
Хорошо известно, что поперечные и продольные компоненты рчлаксируют с разными скоростями ( T2 - определяет потерю фазовой памяти в системе, T1 - связано с энергетическим балансом и определяет стремление системы к термодинамическому равновесию. Когда система возбуждается несколькими последовательными импульсами, поведение компонент энергетического спина в любой момент времени может быть определено поэтапным рещением уравнения (3) методом, хорошо разработанным в теории ядерного магнитного резонанса /14/. После этого неравновесная поляризация среды 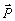 и разность населенности уровней рабочего перехода могут быть определены из и разность населенности уровней рабочего перехода могут быть определены из
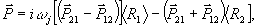 (5) (5)
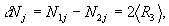 (6) (6)
где 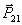 , , 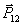 - матричные элементы электрического дипольного момента; N1j, N2j - концентрации тастиц на нижнем и верхнем уровнях во время переходного процесса. При этом N1j+N2j=N0j, N0j - концентрация частиц. Эти выражения могут быть использованы для определения как формы спектрального коэффициента поглощения (а следовательно, отклика системы на действие пробного лазерного импульса с произвольной частотой ω, которая попадает в полосу поглощения перехода), так и когерентных откликов системы типа фотон-эха и индукции. В случае произвольного характера уширения перехода коэффициент поглощения κ(ω) может быть записан в виде - матричные элементы электрического дипольного момента; N1j, N2j - концентрации тастиц на нижнем и верхнем уровнях во время переходного процесса. При этом N1j+N2j=N0j, N0j - концентрация частиц. Эти выражения могут быть использованы для определения как формы спектрального коэффициента поглощения (а следовательно, отклика системы на действие пробного лазерного импульса с произвольной частотой ω, которая попадает в полосу поглощения перехода), так и когерентных откликов системы типа фотон-эха и индукции. В случае произвольного характера уширения перехода коэффициент поглощения κ(ω) может быть записан в виде
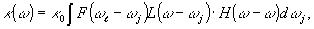 (7) (7)
где 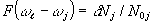 , а , а 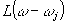 и и 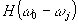
соответственно, нормированные на единицу функции формы линии однородного и неоднородного уширения, ω0 - центральная частота неоднородно уширенной линии. Как будет видно из дальнейшего, функция F(ωl-ωj) имеет сложную зависимость от расстройки резонанса. Поэтому выражение (7) может быть значительно упрощено
лишь в двух предельных случаях.
1 . Неоднородное уширение пренебрежимо мало по сравнению с однородным (Т2< <Т2*), где Т2* - обратная величина полуширины спектра неоднородного уширения.
Из выражения в этом случае (при ωj~ω0) спектральный коэффициент относительного поглощения (7) имеет вид:
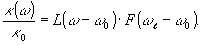 (8) (8)
Здесь функция F(ωl-ω0) не зависит от частоты ω. Она является коэффициентом, величина которого определяется расстройкой частоты возбуждающего поля от резонансной частоты перехода.
2. Обратный случай (Т 2>> Т2*) приводит к зависимости
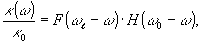 (9) (9)
где функция Г( ωl-ω) характеризует спектральную форму провала "выжигания" на гауссовой линии поглощения H(ω0- ω). Этот случай будет представлять для нас большой практический интерес, так как он соответствует длинным временам фазовой памяти атомной системы. Перейдем непосредственно к нахождению конкретной формы коэффициента поглощения изучаемого перехода после воздействия на систему двумя импульсами когерентного света.
2. Переходный коэффициент поглощения при наличии
расстройки от резонанса ( Δ≠0)
Предположим, что поле накачки имеет вид:
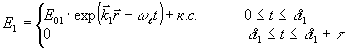
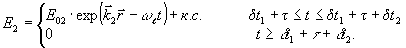
Аналитические решения для функции F(Δ) трудно получить из выражений (2а), (3), (4), (6) в общем виде. Однако, прибли-
женные аналитические решения могут быть получены, если предположить, что волны накачки являются сильными полями. Это предположение практически хорошо оправдано при условии Gμ>>1, где Gμ=(ΩμТ2) 2 - параметр насыщения; Ωμ=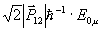 - резонансная частота Раби; μ = 1,2. При этом предположении поэтапное решение уравнения (3) с учетом (4) и (6) для интервала δt1+τ≤t≤δt1+τ+δt2 т.е. во время действия второго импульса приводит к - резонансная частота Раби; μ = 1,2. При этом предположении поэтапное решение уравнения (3) с учетом (4) и (6) для интервала δt1+τ≤t≤δt1+τ+δt2 т.е. во время действия второго импульса приводит к
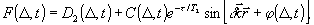 (10) (10)
где F(Δ,t) имеет вид пространственной решетки с периодом 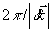 , , 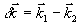 . Амплитуда и фаза этой решетки непрерывно изменяются во времени нелинейным образом. Глубина пространственной модуляции зависит от степени потери фазовой памяти системой к моменту прихода второго импульса (δt1+τ). Коэффициенты в выражении (10) имеют следующий вид: . Амплитуда и фаза этой решетки непрерывно изменяются во времени нелинейным образом. Глубина пространственной модуляции зависит от степени потери фазовой памяти системой к моменту прихода второго импульса (δt1+τ). Коэффициенты в выражении (10) имеют следующий вид:
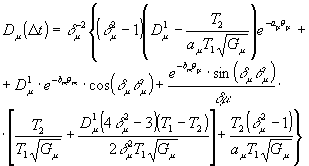
где 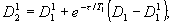
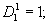 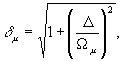 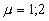
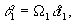 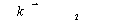
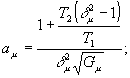
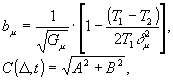
(11б)
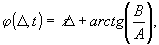
(11с)
где
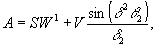
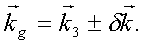
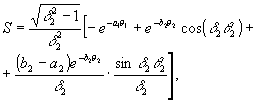
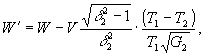
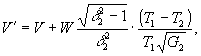
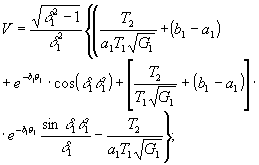
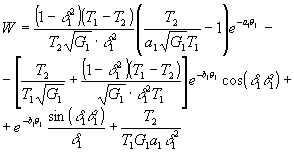
Общие выражения, полученные без каких-либо ограничений, кроме условия для параметра насыщения Gμ>1, довольно громоздки. Поэтому анализ динамики поведения параметров решетки в общем виде затруднен. Можно получить более простые выражения для параметров решетки, если пренебречь релаксацией поперечных компонент во время действия импульсов, а также продольной релаксацией в промежутке между ними. Вследствие того. что δt≈0 такое упрощение справедливо (с точностью до 5%). В таком случае, полагая, что во время действия импульсов δtμ<<T2 и τ<<T1 мы имеем:
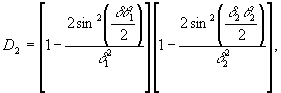 (12a) (12a)
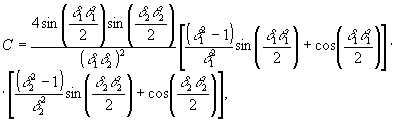 (12 (12
б)
где 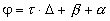 (12c) (12c)
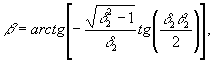
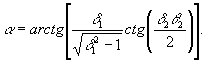
Рассмотрим нестационарное поглощение перехода, которое в соответствии с выражением (7) определяется поведением функции F(Δ,t).
1 . Однородное уширение (Т2<< Т2*, ωj~ω0). В соответствии с (8) относительное поглощение на изучаемом переходе имеет вид:
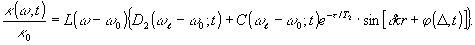 (13) (13)
Как видно из этого выражения, характер поведения решетки не зависит от ω. Поэтому пробные лучи любой частоты и будут взаимодействовать с этой решеткой одинаковым образом. В случае τ>>Т2 решетка вообще не будет формироваться (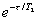 →0). В случае точного резонанса Δ=0 (ωl →0). В случае точного резонанса Δ=0 (ωl= ω0, δμ=1) из выражений (10) и (11) при пренебрежении членами второго порядка малости можно получить:
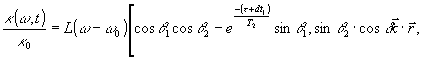 (14) (14)
что совпадает с полученным в / 10/ результатом. Однако случай большого однородного уширения не очень интересен, так как времена фазовой "памяти" при этом малы, а следовательно,выполнение условия (1) затруднено. Практически это означает, что времена задержки должны быть минимальны (τ→0). В этом случае оба импульса возбуждения могут действовать на атомную систему одновременно, т.е. мы приходим к известному случаю обычных динамических индуцированных решеток /4/.
2. Более интересен случай преобладания неоднородного характера уширения (рис.1). Этот случай реализуется в газах при низких давлениях, а в твердых телах только при низкой температуре (например, рубин при 4°К). Поглощение в этом случае определяется выражениями (9) и (10) и в случае гауссового характера неоднородного уширения будет иметь вид:
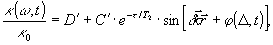 (15) (15)
где 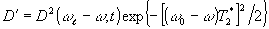
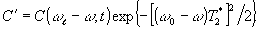
Отсюда следует, что на спектральной кривой неоднородного уширения появляются дыры "выжигания", глубина которых также периодически модулирована по пространству. Распространяясь в такой среде, пробный луч с частотой ω и волновым вектором 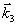 будет дифрагировать на решетке (15) в направлениях будет дифрагировать на решетке (15) в направлениях 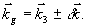 . При этом его распространение в прямом направлении . При этом его распространение в прямом направлении  будет зависеть от величины D' в данный момент времени, а интенсивность дифрагированных пучков будет определяться параметром С'. будет зависеть от величины D' в данный момент времени, а интенсивность дифрагированных пучков будет определяться параметром С'.
Для получения общего представления о характере пространственно частотно временных изменений, происходящих в среде во время действия второго импульса, мы провели численный анализ для 4A 2- 2E перехода в разбавленном рубине (T2*=10-10 C, Т2=10 -7С при 4°К; Т1=3∙10 -3C, |  |= 4,28∙10 -21 ед. CGSE).
При таком расчете мы рассматривали один частный случай, когда первый импульс возбуждения переводит систему атомов в максимум суперпозиционного состояния ( Ω1=1,5∙10 8 С-1, δt1= 10 нc, θ=π/2), а второй импульс при той же длительности (10 нc) имеет амплитуду напряженности поля в 6 раз больше по сравнению с первым импульсом (Ω2=10 9С-1). При таком выборе за время действия второго импульса его импульсная площадь может изменяться от нуля до 3π. На рис.2 приведены спектральные формы кривых D'(Δ) при различных условиях возбуждения. В отличие от накачки одним импульсом (см.,например, /16/) при двухимпульсном возбуждении "дыры" выжигания имеют более сложную частотную структуру (например, при θ2=2 π провал состоит из 3-х пиков поглощения, а при θ2=π из 2-х пиков усиления). В течение действия второго импульса накачки поглощение для прямопроходящей
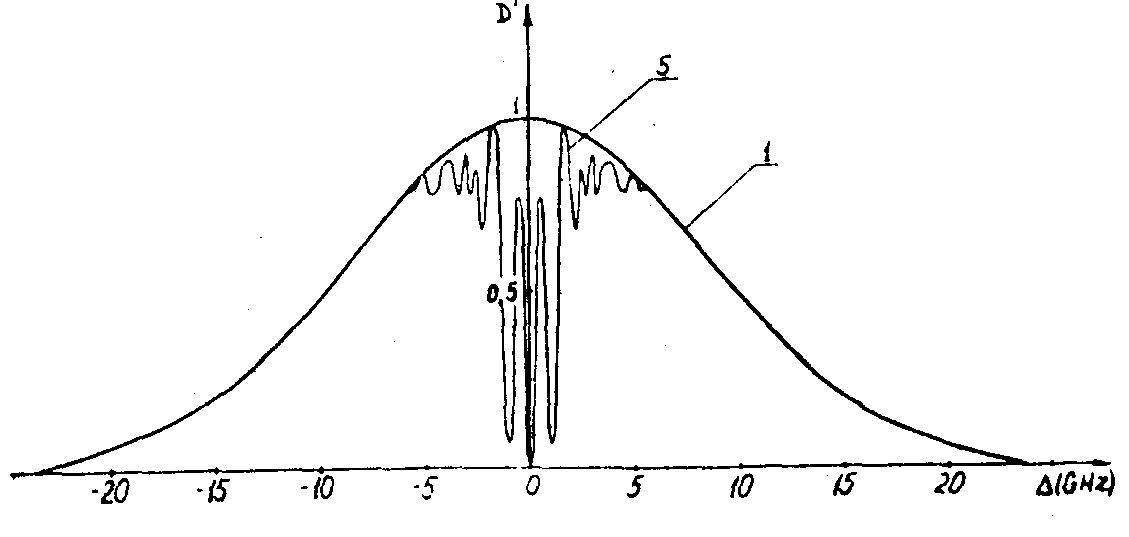
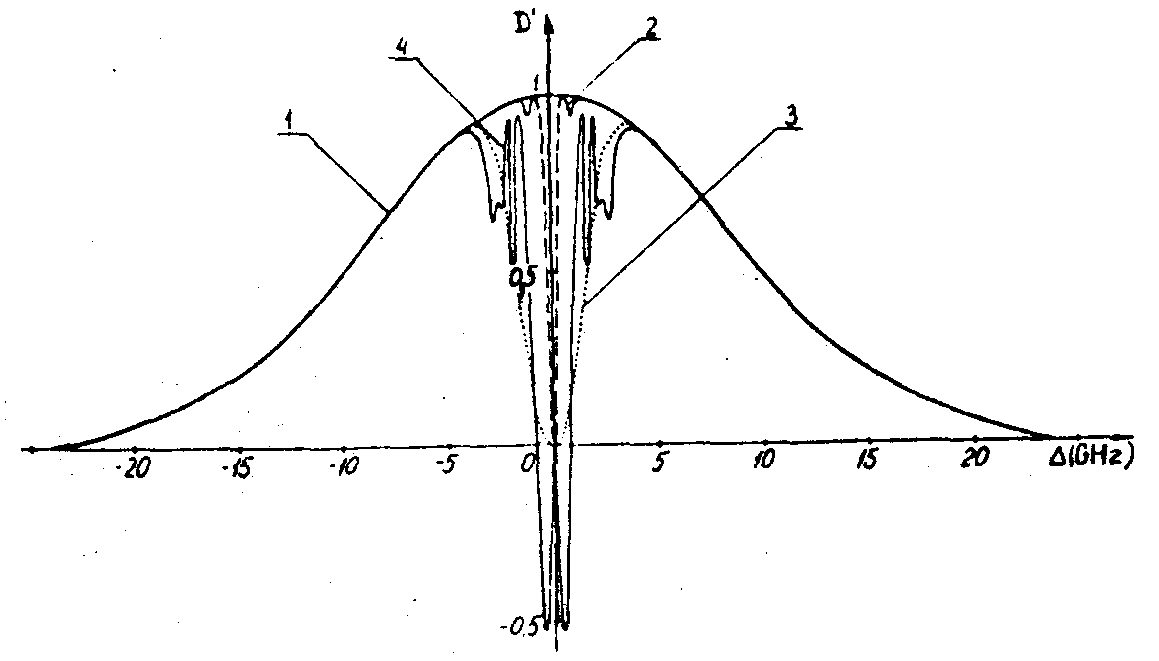
Рис.2. Спектральный коэффициент поглощения D'(ω)
при центральном возбуждении перехода ( ω0=ωl) и θ1= π/2:
1 - Гауссова форма линии; 2 - θ2=0;
3 - θ2=π/2; 4 - θ2=π; 5 – θ2=2π.
волны (вектор 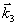 ) периодически изменяется во времени с периодом, зависящим от расстройки T=2π/δμ (рис.3). Что касается волн, дифрагированных в направлениях ) периодически изменяется во времени с периодом, зависящим от расстройки T=2π/δμ (рис.3). Что касается волн, дифрагированных в направлениях 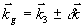 , то их интенсивность зависит от глубины пространственной модуляции решетки, т.е. от С', поведение которой приведено на рис.4. Наиболее , то их интенсивность зависит от глубины пространственной модуляции решетки, т.е. от С', поведение которой приведено на рис.4. Наиболее
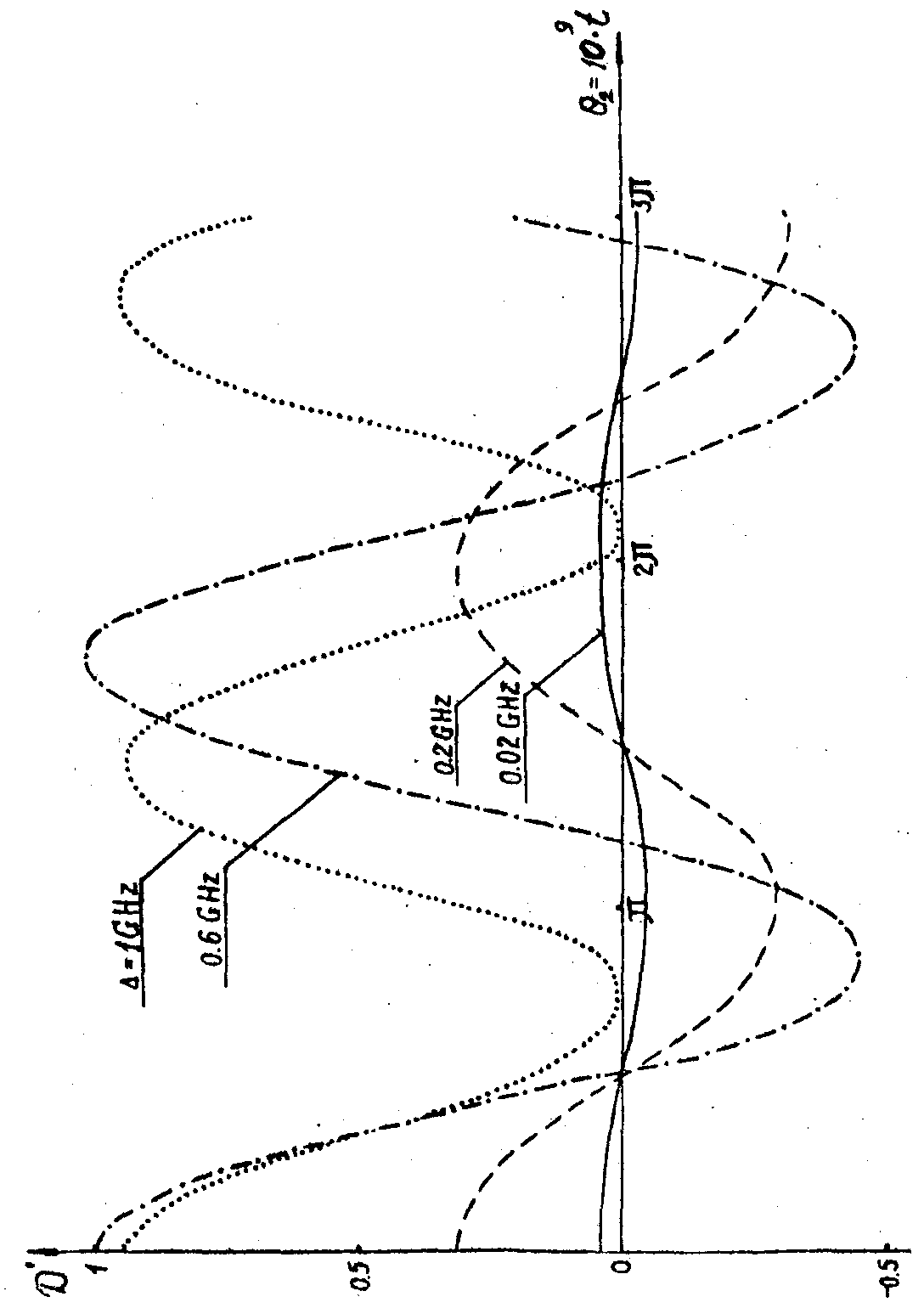
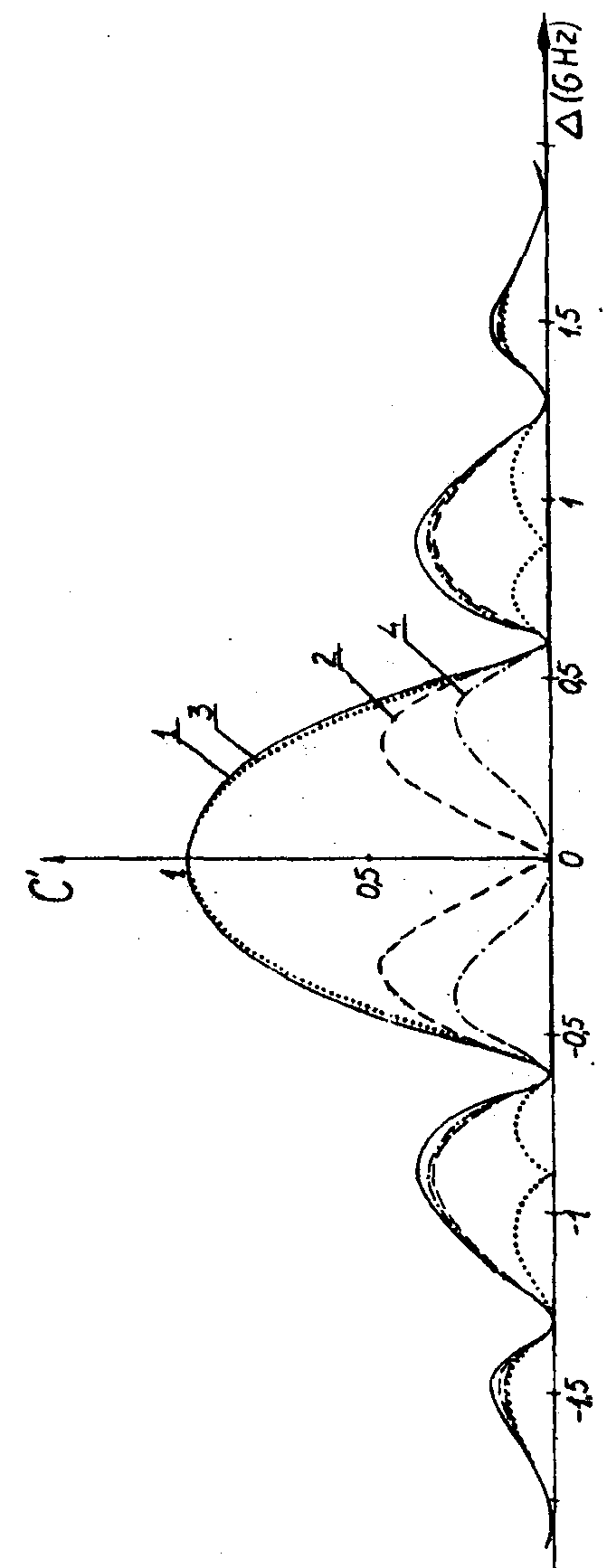
глубокая модуляция может быть достигнута при точном резонансе. На атомах, собственные частоты которых отстоят от резонанса более, чем на 2´
109 гц, решетка практически не образуется. Следует еще раз отметить, что имеются группы атомов, которые вообще не участвуют в процессе образования решеток (в любой момент времени С=0). Поэтому пробный луч с частотой ω, соответствующей таким расстройкам, проходит через среду без отклонения. Не только амплитуда, но и сдвиг решеток в пространстве зависит от величины расстройки. Как видно из (12с), сдвиг решеток по фазе определяется двумя причинами: расфазировкой колебаний атомов во время действия импульсов (β+α) и в промежутке между импульсами (Δτ), которая играет определяющую роль (в случае δtμ<<τ). Зависимость набега фазы от расстройки представлена на рис.5 (для θ1=θ2=π/2).
В течение действия второго импульса амплитуда решеток изменяется во времени с периодом, зависящим от величины расстройки (Т=2 π/δμ). Следовательно, решетки периодически формируются и исчезают (рис.5). Синхронно с этим изменяется фаза решеток, которая определяет положение их в пространстве. Изменение фазы во времени означает, что во время действия второго импульса решетки, формируемые при Δ=Ø, äвижутся в пространстве. При этом скорость их движения изменяется во времени нелинейно.
При точном резонансе фазы не зависят от времени. В начальный момент времени (t=δt1+τ) φ=-90° и, как следует из (12), решетка косинусоидальна и неподвижна. Таким образом,частицы, находящиеся в резонансе с полем, участвуют в формировании неподвижной в пространстве решетки, амплитуда которой пульсирует во времени вплоть до того момента, пока не будет снято возбуждение (t≥δt1+τ+δt2). В то же время отстоящие от резонанса частицы участвуют в образовании бегущих пространственных решеток с изменяющейся во времени амплитудой, которые также прекращают свое движение при t=δt1+τ+δt2. Как следует из выражения (12с), φ(Δ)=-φ(-Δ). Это означает, что различные группы атомов, расположенные по обе стороны от частоты возбуждения, участвуют в образовании решеток, движущихся навстречу друг другу.
В момент окончания второго импульса все движущиеся решетки
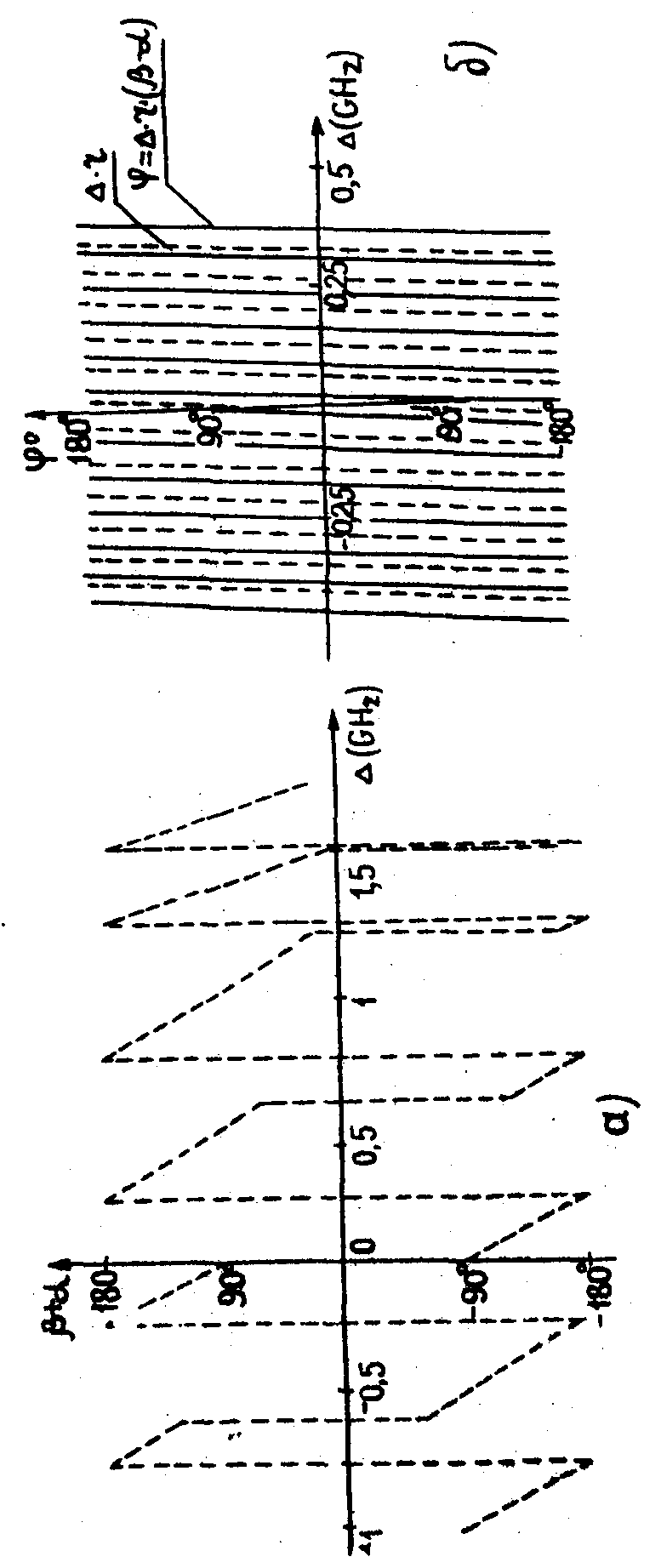
останавливаются и в среде фиксируется "замороженная" сложная интерференционная картина. Она соответствует спектрально-пространственным изменениям коэффициента поглощения среды и медленно распадается со скоростью продольной релаксации. На рис.6 показано пространственное изменение коэффициента поглощения для Δ=0; 0,5∙109 гц при различных условиях возбуждения. Например, в случае точного резонанса сдвиг решетки в пространстве на π/2 происходит при θ2= π и соответствует смене областей усиления и поглощения.
3. Взаимодействие света с решетками
а) Дифракция пробной волны
Подготовленная таким образом среда является пространственным модулятором света для любой слабой пробной волны, частота которой лежит в контуре поглощения среды. Поэтому, как и в обычном случае индуцированных решеток /4/, здесь будет иметь место дифракция пробной волны на решётке. В случае κ0l<<1, где l - толщина образца, амплитуда пробной волны на выходе из среды будет иметь вид /17/:
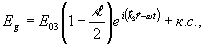 (16) (16)
где E03 - амплитуда пробной волны на входе в среду. Отсюда, совместно с выражением (15), видно, что пробный луч после прохождения через среду разбивается на три волны.
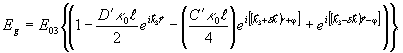 (17) (17)
Первый член дает изменение амплитуды прямопроходящей волны (в направлении 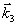 ), а второй соответствует обоим дифрагированным пучкам в направлениях ), а второй соответствует обоим дифрагированным пучкам в направлениях 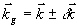 . В случае преобладания неоднородного уширения каждого из дифрагированных пучков для амплитудной дифракционной эффективности будем иметь выражение: . В случае преобладания неоднородного уширения каждого из дифрагированных пучков для амплитудной дифракционной эффективности будем иметь выражение:
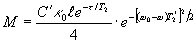 (18) (18)
Рис.6. Временное поведение амплитуд и фаз решеток:
а - C'(Δ,t); α – φ(Δ,t) при θ2=π/2.
Например, ддя розового рубина с концентрацией Gr3+ 0,05 ат.% κ=0,4 см-1. При l=0,1 см, τ=5∙10-8 c., Т2=10 -7 с., ω0=ωl, Δ=2∙107 гц, θ1= θ2= π/2 коэффициент С'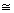 1, а значение М=0,6%. Это значение может быть существенно повышено увеличением концентрации активных центров. 1, а значение М=0,6%. Это значение может быть существенно повышено увеличением концентрации активных центров.
в) Самодифракция
Во время действия второго импульса накачки, как и в обычных динамических решетках,следует ожидать явления самодифракции /4/ этого луча в направлениях 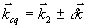 т.е. т.е. 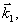 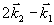 . Если в (13) положить ω=ωl, мы имеем случай точного резонанса. Это значит, что самодифракция второго импульса происходит на неподвижной косинусоидальной решетке с амплитудной эффективностью, пульсирующей во времени, . Если в (13) положить ω=ωl, мы имеем случай точного резонанса. Это значит, что самодифракция второго импульса происходит на неподвижной косинусоидальной решетке с амплитудной эффективностью, пульсирующей во времени,
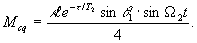 (19) (19)
Отсюда следует, что, измеряя амплитуду и частоту Ω2 сигнала самодифракции при различных задержках τ, можно непосредственно замерять как время поперечной релаксации, так и частоту Раби. Первое позволяет определить ширину однородного уширения, скрытого неоднородным уширением, а второе дает значение дипольного момента для данного перехода.
с) Поляризация
Кроме сигналов оамодифракции, которые являются результатом пространственной модуляции волнового фронта второго пучка света после прохождения среды, рассмотрим электромагнитные поля, возникающие вследствие переизлучения всеми группами атомов, которые входят в спектр "дыры" выжигания F(Δ). Эти поля могут давать ощутимый вклад в самодифракцию только в случае, когда переизлучение носит когерентный характер. Поэтому рассмотрим только ту часть когерентной наведенной поляризации среды, которая является аналогом вынужденной индукции Блоха. Неравновесная поляризация среды в первом приближении достаточно хорошо описывается выражением (5) и качественный характер ее поведения может быть
рассмотрен для частного простого случая, когда неоднородное уширение отсутствует. В этом случае отклик вынужденной индукции во время действия второго импульса накачки будет иметь качественный вид (см.вторую ссылку в /10/):
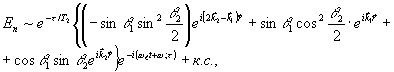 (20) (20)
т.е. состоит из трех волн, из которых две первые распространяются в тех же направлениях, что и волны самодифракции. Характерно, что в отличие от волн самодифракции амплитуды волн вынужденной индукции во времени изменяются неодинаково, их сумма сохраняется постоянной и это говорит о перекачке энергии из одной волны в другую. В случае наличия неоднородного уширения суммарное поле, определяемое макроскопической поляризацией, следует получать путем интегрирования выражения (20) по частотам ωj, предварительно заменив θμ на обобщенную импульсную "площадь" δμθμ(μ=1; 2). Результат интерференции полей в этом случае будет отличен от нуля только при незначительном разбросе начальных фаз δωjτ, т.е. при δωjτ<<π/2. В противном случае (δωjτ~π/2) результат интегрирования равен нулю, а, следовательно, решетка макроскопической поляризации отсутствует и остаются только волны самодифракции.
д) Восстановление волновых фронтов света
До сих пор мы рассматривали взаимодействие плоских волн. В случае, когда волны накачки имеют сложный волновой фронт, несущий фазовую информацию о каком-либо объекте, то формируемая решетка будет являться динамической голограммой. Эта сторона вопроса подробно была рассмотрена в /10/. Информация об объекте будет сохраняться в решетке в течение времени продольной релаксации, т.е. пока система атомов полностью не перейдет в состояние термодинамического равновесия. В течение всего этого времени эта информация может быть восстановлена, либо в дифрагированной
на решетке части любой пробной плоской волны, либо в волнах самодифракции, либо в когерентных откликах системы (индукции и фотон-эха). В конкретном случае, когда волновой фронт первого по времени пучка имеет сложный характер (объектная волна), а второй пучок является плоской волной (референтная волна) при дифракции плоской пробной волны в направлении 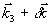 будет распространяться прямая водна, т.е. ее волновой фронт совпадает с фронтом объектной волны, а в направлении будет распространяться прямая водна, т.е. ее волновой фронт совпадает с фронтом объектной волны, а в направлении 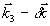 восстановится обращенная волна (волновой фронт комплексно сопряжен фронту объектной волны). Поскольку при таком порядке подачи волн накачки второй пучок имеет плоский фронт, поле самодифракции будет иметь такой же характер волновых фронтов ( восстановится обращенная волна (волновой фронт комплексно сопряжен фронту объектной волны). Поскольку при таком порядке подачи волн накачки второй пучок имеет плоский фронт, поле самодифракции будет иметь такой же характер волновых фронтов (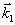 - прямая, - прямая, 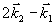 - обращенная волны). То же самое относится к вынужденной индукции в этих направлениях. Ранее говорилось о перекачке энергии при индукции. Действительно, при θ1=π/2 последний член в выражении (20) обращается в нуль вне зависимости от θ2. Поэтому при изменении θ2=Ω2(t-τ-δt1 - обращенная волны). То же самое относится к вынужденной индукции в этих направлениях. Ранее говорилось о перекачке энергии при индукции. Действительно, при θ1=π/2 последний член в выражении (20) обращается в нуль вне зависимости от θ2. Поэтому при изменении θ2=Ω2(t-τ-δt1) во времени энергия попеременно перекачивается из прямой волны вынужденной индукции в обращенную и обратно. Например, при θ1= θ2=π/2 эти волны имеют одинаковую интенсивность. В этом режиме решетка населенности, как следует из рис.8 для Δ=0, имеет максимальную глубину пространственной модуляции и состоит из периодически чередующихся областей поглощения и усиления. Дальнейшее увеличение θ2 приводит к росту интенсивности обращенной волны и к соответственному падению для прямой волны. При θ2=π вся энергия вынужденной индукции сосредоточена в обращенной волне. Интересно, что в это время решетка населенности в резонансе полностью исчезает (см.выражение (14)). Дальнейшее увеличение θ2 сопровождается появлением решетки, а также прямой волны в направлении 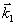 . Как видно из рис.6 (при Δ=0), инверсные и поглощающие участки решетки при этом меняются местами. Далее процесс периодически повторяется. . Как видно из рис.6 (при Δ=0), инверсные и поглощающие участки решетки при этом меняются местами. Далее процесс периодически повторяется.
Возможность восстановления сложных волновых фронтов в сигналах фотон-эха, впервые показанная в работах /18/, также, по-видимому, базируется на явлении формирования индуцированных транзиент-№ решеток. Рассмотрим конкретный случай, когда при условии (1) объектная волна подается раньше опорной и имеет волновой
фронт произвольной формы:
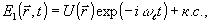 (21) (21)
где 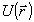 - фазор объектной волны, который содержит полную информацию об объекте. При этом предполагаем, что преобладает неоднородный характер уширения перехода (рис.1). В этом случае когерентный отклик системы на возбуждение двумя импульсами на интервале t>δt1+τ+δt2 (т.е. когда установилась система неподвижных в пространстве решеток) при δtμ<<τ будет иметь вид /18/: - фазор объектной волны, который содержит полную информацию об объекте. При этом предполагаем, что преобладает неоднородный характер уширения перехода (рис.1). В этом случае когерентный отклик системы на возбуждение двумя импульсами на интервале t>δt1+τ+δt2 (т.е. когда установилась система неподвижных в пространстве решеток) при δtμ<<τ будет иметь вид /18/:
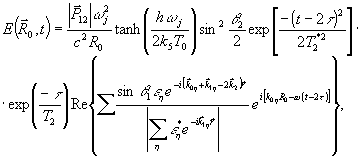 (22) (22)
где 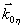 есть волновой вектор η-ой компоненты этого поля, a εη и есть волновой вектор η-ой компоненты этого поля, a εη и 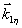 определяют пространственный фурье-спектр объектной волны, определяют пространственный фурье-спектр объектной волны,
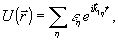 (23) (23)
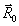
- радиус-вектор точки наблюдения. Поле 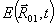 найдено для дальней зоны найдено для дальней зоны 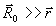 , где , где 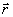 - радиус-вектор произвольной точки излучающего объема. Импульсные площади накачки имеют вид: - радиус-вектор произвольной точки излучающего объема. Импульсные площади накачки имеют вид:
 (24) (24)
Из выражения (22) следует, что поле когерентного отклика 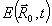 отлично от нуля только вблизи t=2τ и каждая компонента фурье-спектра пространственных частот этой волны подчиняется условию отлично от нуля только вблизи t=2τ и каждая компонента фурье-спектра пространственных частот этой волны подчиняется условию 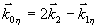 . При учете этого условия после интегрирования по индексу " ", т.е. по всему объему образца можно получить . При учете этого условия после интегрирования по индексу " ", т.е. по всему объему образца можно получить
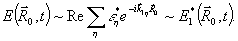 (25) (25)
Следовательно, этот сигнал, называемый первичное фотон-эхо, содержит псевдоскопическое изображение объекта. Если изменить порядок подачи импульсов накачки, то волновой фронт первичного фотон-эха уже не будет содержать информацию об объекте в явном виде. Условие фазового синхронизма особенно важно для правильного восстановления волновых фронтов, так как векторы 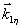 могут иметь различные углы по отношению могут иметь различные углы по отношению 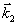 и поэтому не все компоненты могут быть восстановлены в сигнале первичного фотон-эха. Это связано с тем, что первичное эхо наблюдается только при малых углах между возбуждающими импульсами. Это ограничение может быть устранено в случае стимулированного фотон-эха. Стимулированное фотон-эхо - это когерентный отклик системы атомов, который возникает, если образец облучить еще одним импульсом света (см. рис.7). Этот отклик возникает спустя время τ после подачи третьего импульса (τse=τ31+τ), где τ=τ21-δt1). Положение импульсов на рис.8 соответствует случаю коротких импульсов δtμ<<τ. Как показано в /18/, точное восстановление волнового фронта можно осуществить в отклике стимулированного эха, если объектная волна действует позже опорной (теперь уже и поэтому не все компоненты могут быть восстановлены в сигнале первичного фотон-эха. Это связано с тем, что первичное эхо наблюдается только при малых углах между возбуждающими импульсами. Это ограничение может быть устранено в случае стимулированного фотон-эха. Стимулированное фотон-эхо - это когерентный отклик системы атомов, который возникает, если образец облучить еще одним импульсом света (см. рис.7). Этот отклик возникает спустя время τ после подачи третьего импульса (τse=τ31+τ), где τ=τ21-δt1). Положение импульсов на рис.8 соответствует случаю коротких импульсов δtμ<<τ. Как показано в /18/, точное восстановление волнового фронта можно осуществить в отклике стимулированного эха, если объектная волна действует позже опорной (теперь уже 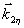 является пространственной компонентой фурье-спектра). При этом условие фазового синхронизма имеет вид: является пространственной компонентой фурье-спектра). При этом условие фазового синхронизма имеет вид: 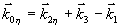 . Это условие иллюстрируется на рис.9 для случая, когда вое три вектора ( . Это условие иллюстрируется на рис.9 для случая, когда вое три вектора (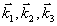 ) лежат в одной плоскости. По условию синхронизма может существовать только такой вектор, конец которого лежит на окружности с центром O1 и радиусом ) лежат в одной плоскости. По условию синхронизма может существовать только такой вектор, конец которого лежит на окружности с центром O1 и радиусом  и только в пределах дуги, пересекающей заштрихованную область (отрезок OO' равен и только в пределах дуги, пересекающей заштрихованную область (отрезок OO' равен 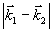 , т.е. зависит от угла между векторами , т.е. зависит от угла между векторами 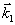 и и 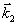 ). Ширина этой области определяется, размером дыры "выжигания" на линии поглощения перехода ( ). Ширина этой области определяется, размером дыры "выжигания" на линии поглощения перехода (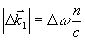 , где Δω - ширина дыры, n - коэффициент преломления). Вектор , где Δω - ширина дыры, n - коэффициент преломления). Вектор 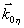 может девать в угловой области, ограниченной векторами может девать в угловой области, ограниченной векторами 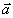 и и 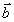 , т.е. восстанавливающий пучок ( , т.е. восстанавливающий пучок (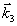 ) должен находиться только в области между векторами ) должен находиться только в области между векторами 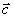 и и 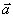 . В частности, если . В частности, если 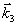 на- на-
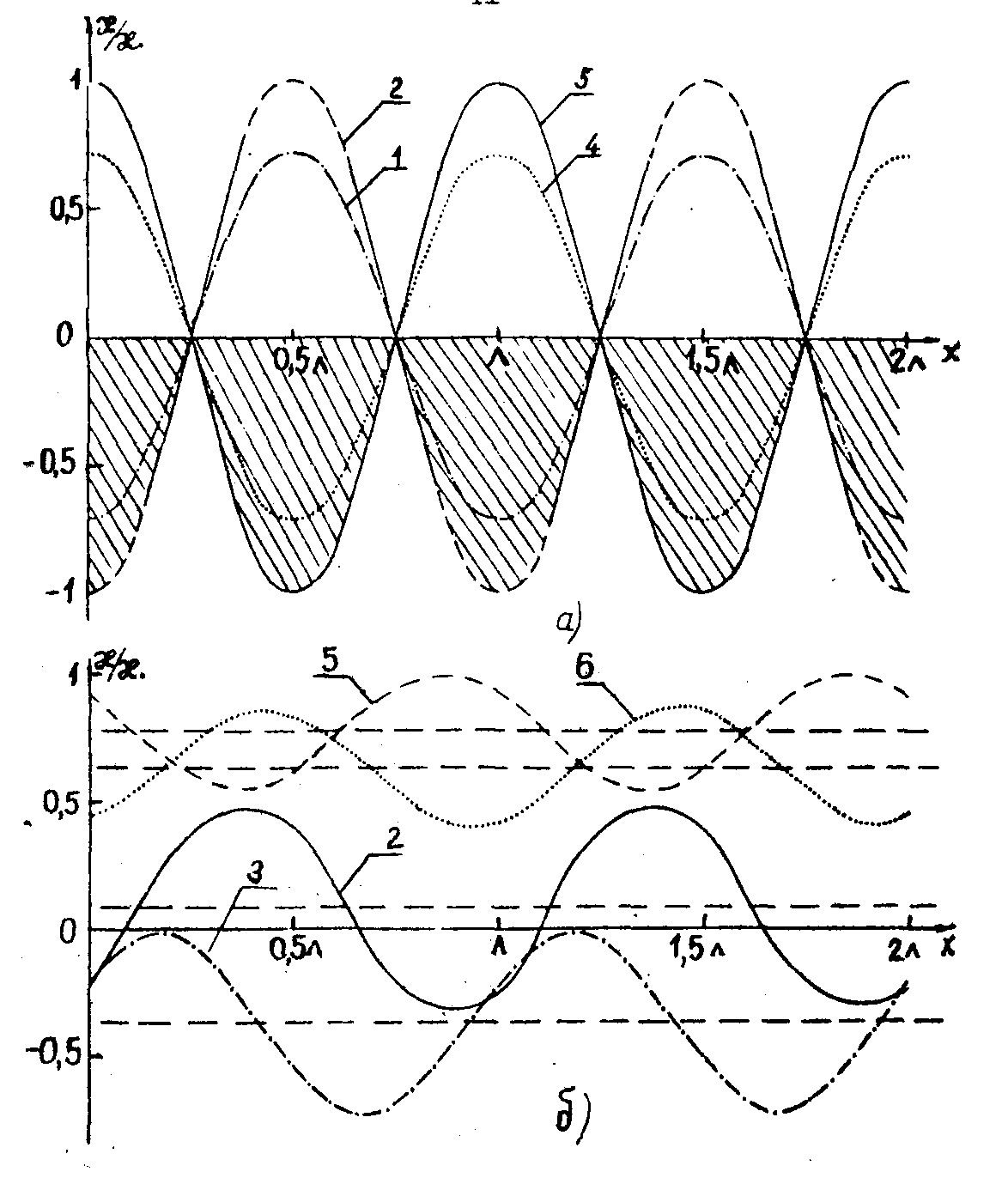
Рис.7. Пространственное распределение относительного
поглощения
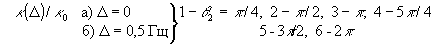
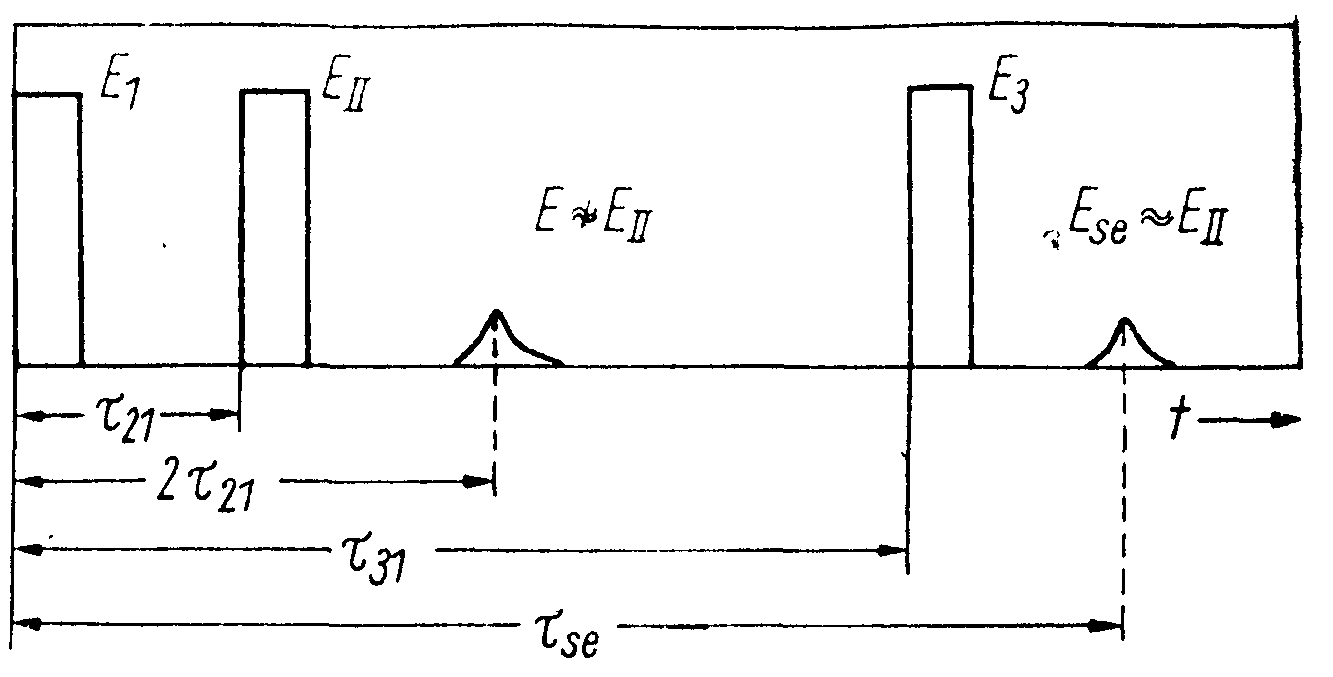
Рис.8. Возбуждение системы атомов тремя когерентными импульсами света.
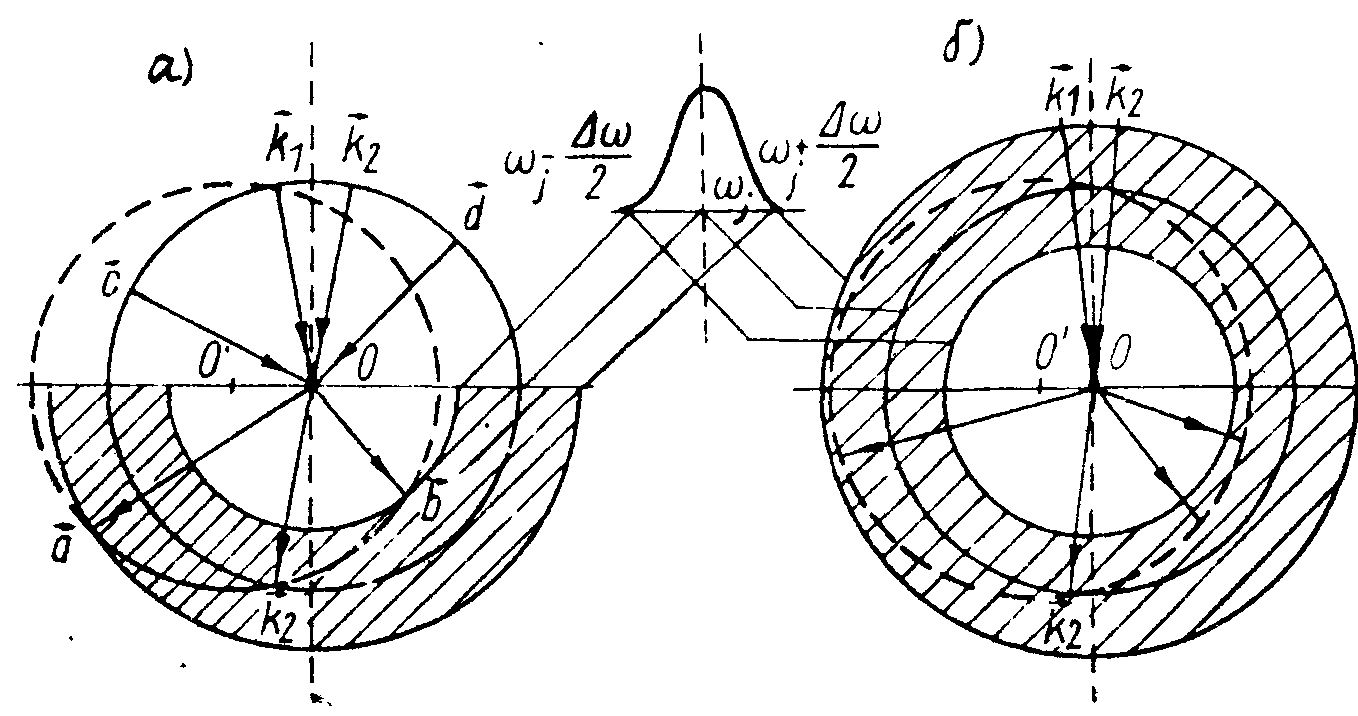
Рис.9. Условия фазового синхронизма.
править вдоль 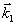 , стимулированное эхо будет наблюдаться в направлении , стимулированное эхо будет наблюдаться в направлении 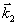 и будет соответствовать центру дыры "выжигания", т.е. и будет соответствовать центру дыры "выжигания", т.е. 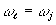 . При малых углах между . При малых углах между 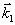 и и 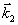 это ограничение устраняется (рис.9б), т.к. уже вся окружность попадает в заштрихованную область. Это значит, что восстанавливающий луч может иметь любой направление. При смене порядка подачи волн накачки условие будет иметь вид: это ограничение устраняется (рис.9б), т.к. уже вся окружность попадает в заштрихованную область. Это значит, что восстанавливающий луч может иметь любой направление. При смене порядка подачи волн накачки условие будет иметь вид: 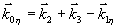 , и при , и при 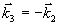 стимулированное эхо имеет полное обращение волнового фронта. стимулированное эхо имеет полное обращение волнового фронта.
4. Э к с п е р и м е н т
Современное развитие лазерной техники позволяет без труда при эксперименте выполнить условие (1), когда, находясь в когерентном состоянии суперпозиции базисных векторов, система атомов может запоминать фазовые характеристики внешних возбуждающих оптических полей. Это особенно ярко проявляется в возможности получения интерферограммы в среде даже в случае, когда оптические импульсы накачки не могут непосредственно интерферировать друг с двугом, например, подаются на среду в разное время. В работе /11/ на примере рубина показана экспериментально возможность создания индуцированной решетки при условии (1). Выбор рубина в качестве объекта обусловлен тем, что при этом условии на переходе 4А2=2Е рубина успешно наблюдались различные переходные резонансные явления (например, фотон-эхо /13,19/), накопленный опыт по которым мог значительно облегчить поиск правильных рабочих режимов, необходимых для создания индуцированных решеток. На рис.10 приведена схема экспериментальной установки, которая принципиально мало отличалась от известных экспериментальных установок по наблюдению фотон-эхо в рубине. В нашем случае самое существенное отличие заключается в способе подачи третьего импульса, который одновременно используется в качестве пробного луча для получения сигналов дифракции на индуцированной решетке, а также для индуцирования сигнала стимулированного фотон-эха спустя время τ после подачи этого импульса. Третий импульс в нашем эксперименте формируется просто отражением второго импульсного пучка, прошедшего через образец, от плоского зеркала. При такой схеме луч III распространяется в одном из брег-
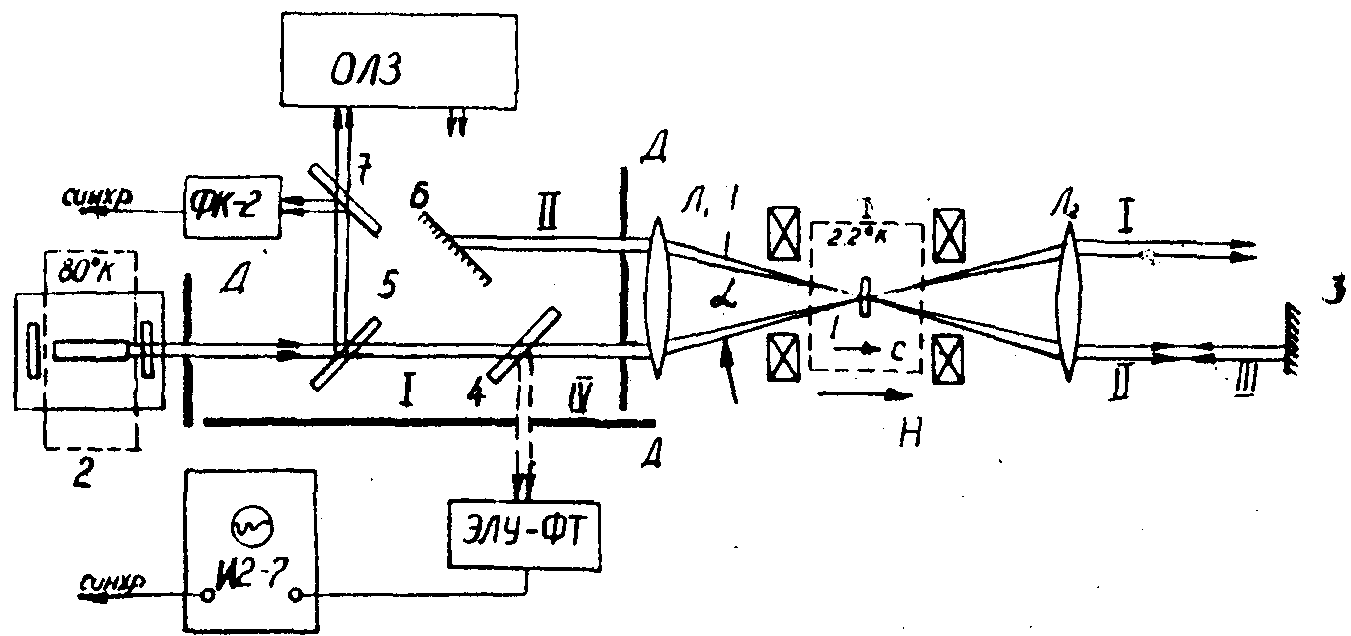
Рис.10. Экспериментальная установка:
1 - образец; 2 - лазер накачки;
4, 5, 7 - светоделители; 3, 6 - зеркала;
ОЛЗ - оптическая линия задержки.
говском направлении. Поэтому, как для дифракции, так и для стимулированного фотон-эха будет точно выполняться условие фазового синхронизма вне зависимости от угла между лучами I и II. Такая схема имеет большие преимущества, так как позволяет использовать толстые образцы, а следовательно, повысить сигнал дифракции (см.выражение(18)). Условие синхронизма одинаково как для дифракции (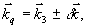 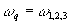 ), так и для стимулированного фотон-эха ( ), так и для стимулированного фотон-эха (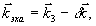 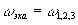 ). Поэтому при такой схеме ( ). Поэтому при такой схеме (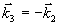 ) из этих условий следует ) из этих условий следует 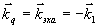 (оба сигнала будут распространяться в направлении IV в после отклонения этого луча IV при помощи полупрозрачного зеркала 4 сигнал может быть эерегистрирован фотоприемником). Подчеркнем, что в этом направлении, кроме этого сигнала, не распространяются ни один из рабочих пучков I, II, III. Это существенно повышало отношение сигнал/шум и позволило в нашем эксперименте обходиться без каких-либо оптических затворов, а ограничиться лишь применением (оба сигнала будут распространяться в направлении IV в после отклонения этого луча IV при помощи полупрозрачного зеркала 4 сигнал может быть эерегистрирован фотоприемником). Подчеркнем, что в этом направлении, кроме этого сигнала, не распространяются ни один из рабочих пучков I, II, III. Это существенно повышало отношение сигнал/шум и позволило в нашем эксперименте обходиться без каких-либо оптических затворов, а ограничиться лишь применением
различных экранов с диафрагмами Д . Оптическая линия задержки ОЛЗ, предназначенная для формирования луча II, с целью предотвращения расходимости этого пучка собрана по конфокальной схеме с базой 4 м. Используемый образец I вырезан перпендикулярно оптической оси 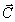 из рубина с концентрацией Cr3+ 0,05 ат.% в виде пластинки толщиной 1,5 мм. Для облегчения выполнения условия (1) образец охлаждается в оптическом криостате до 2,2°К. Это приводит к увеличению времени поперечной релаксации Т2 в рубине не менее, чем до 10-7 с, что позволяет использовать для накачки моноимпульсный рубиновый лазер 2 с длительностью излучения 10 нc и мощностью 1 Мвт. Необходимость охлаждения активного стержня лазера до 80°К вызвана нарушающим условие резонанса смещением линии поглощения перехода 4А2 из рубина с концентрацией Cr3+ 0,05 ат.% в виде пластинки толщиной 1,5 мм. Для облегчения выполнения условия (1) образец охлаждается в оптическом криостате до 2,2°К. Это приводит к увеличению времени поперечной релаксации Т2 в рубине не менее, чем до 10-7 с, что позволяет использовать для накачки моноимпульсный рубиновый лазер 2 с длительностью излучения 10 нc и мощностью 1 Мвт. Необходимость охлаждения активного стержня лазера до 80°К вызвана нарушающим условие резонанса смещением линии поглощения перехода 4А2 - 2Е(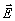 ) рубинового образца 1 при охлаждении его до 2,2°К. Как было показано при исследовании фотон-эха в рубине /19/ при таком режиме охлаждения лазера имеет место резонанс для лазерной линии 6933,97 Å (переход 4A2(Ms=±1/2) при 77°К) и линии поглощения образца 6934 Å (4A2(Ms=±3/2)-2Е( ) рубинового образца 1 при охлаждении его до 2,2°К. Как было показано при исследовании фотон-эха в рубине /19/ при таком режиме охлаждения лазера имеет место резонанс для лазерной линии 6933,97 Å (переход 4A2(Ms=±1/2) при 77°К) и линии поглощения образца 6934 Å (4A2(Ms=±3/2)-2Е(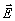 ) при 2,2°К). Все пучки в нашем эксперименте поляризованы перпендикулярно плоскости рис.1, а для создания слабого продольного магнитного поля ( ) при 2,2°К). Все пучки в нашем эксперименте поляризованы перпендикулярно плоскости рис.1, а для создания слабого продольного магнитного поля ( , 0÷250 ãс) используются катушки Гельмгольца. На рис.11 представлены осциллограммы сигналов, соответствующих возбуждающим импульсам I и II (верхний ряд) и когерентным откликам системы (два нижних ряда) в направлении IV. Первый импульс на нижних осциллограммах соответствует дифракции III луча в образце, а второй появляется через время τ, равное интервалу между I и II импульсами, и представляет собой стимулированное фотон-эхо. Мы тщательно проверили, что оба эти импульса не являются следствием каких-либо отражений пучков I, II, III от различных деталей установки. Наиболее убедительным доказательством является то, что оба сигнала не наблюдаются в случае перекрытия хотя бы одного из рабочих пучков I, II, III. Нарушение условия резонанса, например, нагреванием рабочего стержня лазера на несколько градусов, также приводит к исчезновению сигналов дифракции и фотон-эха. Сигналы дифракции и эха возрастают, когда магнитное поле приложено вдоль оси кристалла , 0÷250 ãс) используются катушки Гельмгольца. На рис.11 представлены осциллограммы сигналов, соответствующих возбуждающим импульсам I и II (верхний ряд) и когерентным откликам системы (два нижних ряда) в направлении IV. Первый импульс на нижних осциллограммах соответствует дифракции III луча в образце, а второй появляется через время τ, равное интервалу между I и II импульсами, и представляет собой стимулированное фотон-эхо. Мы тщательно проверили, что оба эти импульса не являются следствием каких-либо отражений пучков I, II, III от различных деталей установки. Наиболее убедительным доказательством является то, что оба сигнала не наблюдаются в случае перекрытия хотя бы одного из рабочих пучков I, II, III. Нарушение условия резонанса, например, нагреванием рабочего стержня лазера на несколько градусов, также приводит к исчезновению сигналов дифракции и фотон-эха. Сигналы дифракции и эха возрастают, когда магнитное поле приложено вдоль оси кристалла  . Расстройка поля от этого направления влияет различным образом на дифракцию и на эхо. Например, смотри осциллограммы . Расстройка поля от этого направления влияет различным образом на дифракцию и на эхо. Например, смотри осциллограммы
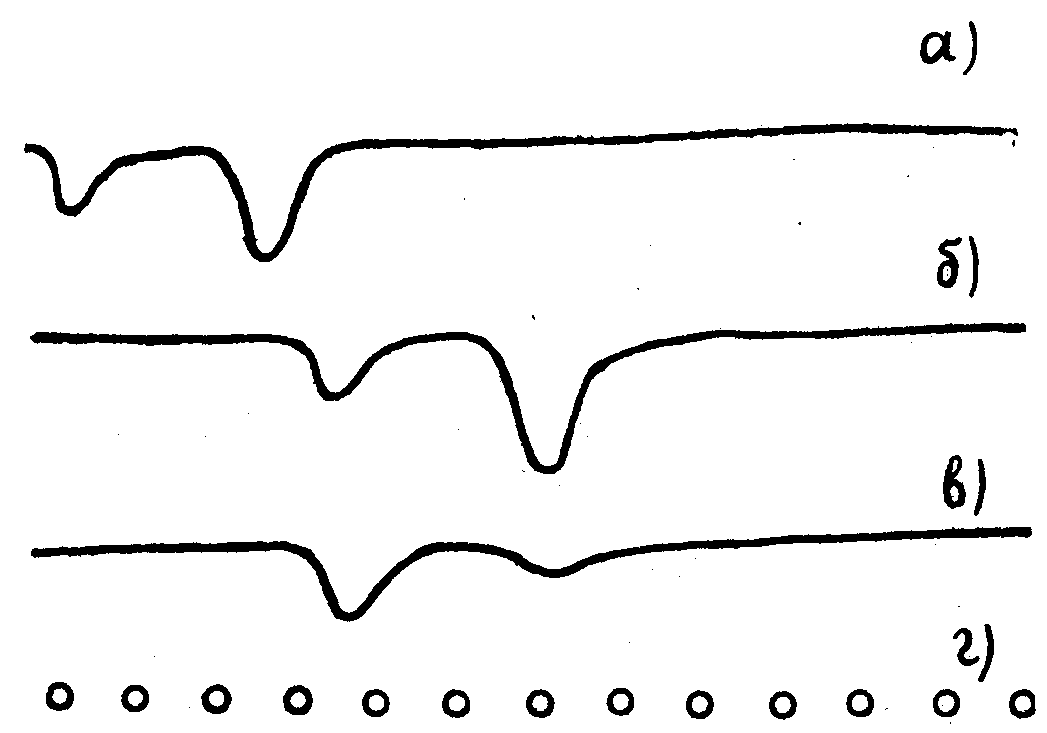
Рис.11. Осциллограммы сигналов, наблюдаемых при возбуждении рубина: τ=50 нc.
(рис.11), полученные при различных углах между полем и осью кристалла. Следует подчеркнуть еще одно обстоятельство. Волны дифракции и фотон-эха имеют обращенные фронты. Это особенно ясно видно из того, что после прохождения через линзу Л1 пучок IV остается параллельным, т.е. имеет плоский волновой фронт.
6. З а к л ю ч е н и е
Таким образом, возбуждая при определенных условиях атомную систему импульсными когерентными полями, разнесенными как в пространстве, так и во времени, можно в среде индуцировать периодические пространственные решетки. Такие решетки формируются вследствие интерференции суперпозиционных состояний только в случае, когда атомная система обладает достаточно долгой памятью
о фазе возбуждающих полей. Амплитуда и скорость движения решетки определяется расстройкой частоты поля накачки от резонанса и зависит от потери когерентности в системе из-за необратимых процессов релаксации. Изучая рассеяние света на таких решетках, можно измерять характеристики переходов (времена поперечной и продольной релаксации, величину дипольных моментов).
Л и т е р а т у р а
1. H.Gerritsen, J.Appl.Phys.Lett., 10, 239, 1967;
14, 159, 1969.
2. H.Boersch, H.Eichler, Z.angew.Phys., 22, 378, 1967.
3. O.Hill, Appl.Opt., 10, 1695, 1971.
4. Е.И.Штырков. Письма ЖЭТФ, 12, 3, 134, 1970.
5. A.Siegman, Appl.Phys.Lett., 30, 1, 21, 1977.
6. J.Woerdman, Opt.Comm., 2, 212, 1970.
7. H.Eichler, G.Salje, H.Stahl, J.Appl.Phys., 44, 5383, 1973.
8. H.Kogelnik, С.Shank, Appl.Phys.Lett., 18, 152, 1971.
9. H.Eichler, Opt.Acta, 24, 6, 631, 1977.
10. Е.И.Штырков. Оптика и спектроскопия, 45, 603, 1978.
Голографические методы исследований. Материалы Х Всесоюзное школы по голографии, Л., ЛИЯФ, 119-130, 1978.
11. Е.И.Штырков, В.С.Лобков, Н.Г.Ярмухаметов. Письма ЖЭТФ, 27, 12, 685, 1978.
12. H.Dicke, Phys.Rev., 93, 99, 1954.
13. I.Abella, Т.Kurnit, S.Hartmann, Phys.Rev., 141, 1, 391, 1966.
14. H.Torrey, Phys.Rev., 76, 1059, 1949.
15. В.Файн. Фотоны и нелинейные среды, т.1, Москва, 1972.
16. Л.Аллен, Дж.Эберли. Оптический резонанс и двухуровневые атомы, "Мир", М., 1978.
17. Е.И.Штырков. Динамическая голография в резонансных средах, № 1145-74, деп.ВИНИТИ, 1974.
18. Е.И.Штырков, В.В.Самарцев. В сб. "Электромагнитное сверхизлучение, Татполиграф, Казань, стр.418, 1975. Оптика и
спектроскопия, 40, 392, 1976; Phys.St.Sol.(a), 45,
647, 1978.
19. N.Kurnit, I.Abella, S.Hartmann, Phys.Rev.Lett., 13, 567, 1964.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

