|
|
 |
 |

|
| |
ОБ УСЛОВИЯХ МАЛОСТИ ШУМОВ ТРЕХМЕРНЫХ ГОЛОГРАММ
В.Г.Сидорович
На основе развитого метода классификации плоских волн поляризации, наводимых светом в объеме трехмерной безопорной амплитудно-фазовой голограммы, по признаку величины рассогласования их фазовых скоростей со световой получена оценка собственных шумов такой голограммы (т.е. шумов, не связанных с дефектами регистрирующей среды). Эта оценка позволила сформулировать условия, налагаемые на параметры регистрирующей среды и записывающего излучения, при выполнении которых собственные шумы безопорной трехмерной голограммы пренебрежимо малы по интенсивности по сравнению с восстановленной волной.
Данные условия необходимо учитывать при разработке устройств для преобразования когерентных световых пучков. Выводы работы находятся в соответствии с имеющимися экспериментальными данными.
Многими авторами отмечалось преимущество трехмерных голограмм по сравнению с плоскими, заключающееся в потенциально более низком уровне их шумов /1-6/. в основе указанного преимущества лежат следующие причины. Восстановление зарегистрированной волны осуществляется, в случае трехмерной голограммы , за счет рассеяния распространяющихся в ней плоских компонентов восстанавливающей волны из пространственных гармониках диэлектрической проницаемости, в записи которых эти компоненты участвовали. Указанные гармоники удовлетворяют по отношению к компонентам восстанавливающей волны условию Брэгга, т.е. эффект рассеяния накапливается по мере распространения волны в голограмме. С другой стороны, искажающие восстановленную волну световые волны порождаются рассеянием компонентов восстанавливающей волны на пространственных гармониках диэлектрической проницаемости голограммы, в записи которых они не
- 162 -
участвовали, а также на неоднородностях регистрирующей среды. При этом волны, рассеянные различными слоями голограммы, вообще говоря, не синфазны, т.е. складываются по интенсивности а не по амплитуде. Если толщина слоя голограммы, дающего заметный вклад в восстановленную волну, существенно превышает толщину слоя, в пределах которого синфазны искажающие волны, то искажения восстановленной волны незначительны. Выводу критериев, обеспечивающих выполнение указанного условия, посвящена данная работа. В основе проведенного рассмотрения лежит метод классификации плоских волн поляризации, наводимых в голограмме восстанавливающей световой волной, по признаку величины рассогласования их фазовых скоростей со скоростью света /7/. Исследование зависимости относительного числа плоских волн поляризации, распространяющихся в трехмерной голограмме , от величины рассогласования их фазовых скоростей со световой, позволило найти параметры эксперимента, от которых зависит уровень шумов голограммы, и сформулировать практические рекомендации по снижению этого уровня. Анализ проведен применительно к однородной регистрирующей среде и лилейной зависимости комплексной, диэлектрической проницаемости голограммы от локальной экспозиции. Если указанная зависимость является нелинейной, то пространственный спектр голограммы, вообще говоря. обогащается значительным числом дополнительных компонентов /8/. Однако и в атом случае остаются в силе развитый метод классификации плоских компонентов волны поляризации а формулы, определяющие величины фазовых скоростей этих волн через взаимные ориентации соответствующих пространственных гармоник диэлектрической проницаемости и рассеивающихся на них плоских световых волн.
1. Выведем дифференциальные уравнения, которым подчиняются амплитуды плоских компонентов светового излучения, распространяющегося в объеме амплитудно-фазовой голограммы.
Предположим, что светочувствительная среда, в которой записывается голограмма, занимает пространство, ограниченное двумя параллельными плоскостями. Расположим ортогональные координатные оси оХ и oY в одной из этих плоскостей, ось оZ направим по нормали к ним в глубину среды. Допустим, что волновые векторы k0,......,kN монохроматических плоских световых волн, распространяющихся
- 163 -
в среде при записи, наклонены на незначительные угля q
0 ,..., q
N по отношению к oZ (волны с векторами kj при j = 0 ,..., К принадлежат к объектному пучку, а при j=K+1,..., N - к опорному). Это допущение, наряду с предположением о том, что все плоские компоненты записывающего и восстанавливающего излучения поляризованы в одной плоскости, позволяет не учитывать векторный характер электромагнитного поля.
Обозначим Е амплитуду электрического поля излучения, записывающего голограмму. В пренебрежении отражением и преломлением на границах среды справедливо соотношение
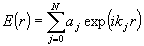 (1) (1)
где a j - комплексные амплитуды плоских компонентов записывающего излучения;
kj = (kjx, kjy, kjz); r = (x,y,z); ℓ ³
Z ³
0
Предположим , что после соответствующей обработки светочувствительная среда изменяет свою комплексную диэлектрическую проницаемость на малую по модулю величину D
e
(r), пропорциональную локальной плотности энергии света при записи:
D
e
(r) = c
e
0|
E(r)|
2 (2)
где e
0 - диэлектрическая проницаемость регистрирующей среды; Jm e
0 =0; c
=Rеc
+iJmc
- комплексный коэффициент пропорциональности.
Подстановка (1) в (2) дает выражение для распределения диэлектрической проницаемости в объеме голограммы
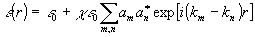 (3) (3)
где |D
e
|
<< e
0; ℓ ³
Z ³
0. Соотношение (3) показывает, что в рассматриваемом случае голограмма представляет собой суперпозиций конечного числа объемных дифракционных решеток, характеризующихся пространственными распределениями комплексной диэлектрической
- 164 -
проницаемости вида
e
mn(r) = 2c
e
0|am||
an|
Cos[(km – kn)r + j
mn] (4)
где j
mn = Аrga m – Аrga n.
Пусть плоские компоненты падающего на голограмму светового пучка совпадают по направлениям распространения с какими-либо плоскими составляющими опорного и объектного пучков, а комплексные амплитуда bS (S=0,...,N) этих компонентов произвольны. Электрическое поле освещающего пучка на поверхности голограммы при этом описывается выражением
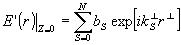 (5) (5)
где 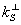 и и 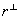 - проекции kS и rS на XoY . Это электрическое поле наводит в объеме голограммы волновое поле поляризации, которое изменяет комплексные амплитуды плоских компонентов освещающего пучка и создает новые плоские световые волну. Так как амплитуды aS, bS плоских световых волн, падающих на поверхность среды при записи и считывании голограммы, не зависят от х и y, то амплитуды плоских компонентов световой волны, распространяющейся в голограмме, могут зависеть только от Z. Кроме того, сдвиг по фазе между всякой плоской световой волной, распространяющейся в объеме голограммы, и возбуждающей ее или взаимодействующей с ней водной поляризации одинаков во всех точках любой плоскости ℓ³
Z ³
0. Поэтому одинаковы проекции на поверхность голограммы фазовых скоростей плоских волн поляризации и связанных с ними световых волн. Отсюда следует, что волновые векторы k’j, k'pqn плоских световых волн, связанных с волной поляризации, наведенной - проекции kS и rS на XoY . Это электрическое поле наводит в объеме голограммы волновое поле поляризации, которое изменяет комплексные амплитуды плоских компонентов освещающего пучка и создает новые плоские световые волну. Так как амплитуды aS, bS плоских световых волн, падающих на поверхность среды при записи и считывании голограммы, не зависят от х и y, то амплитуды плоских компонентов световой волны, распространяющейся в голограмме, могут зависеть только от Z. Кроме того, сдвиг по фазе между всякой плоской световой волной, распространяющейся в объеме голограммы, и возбуждающей ее или взаимодействующей с ней водной поляризации одинаков во всех точках любой плоскости ℓ³
Z ³
0. Поэтому одинаковы проекции на поверхность голограммы фазовых скоростей плоских волн поляризации и связанных с ними световых волн. Отсюда следует, что волновые векторы k’j, k'pqn плоских световых волн, связанных с волной поляризации, наведенной
|
[k’j]XoY = [kj]XoY
[k’pqn]XoY = [kpqn]XoY |
(6) |
- 165 -
где kpqn = kp – kq + kn; p,q,n,j = 0, l ,....., N.
Для нахождения проекций k’j и k’pq,n на оZ необходимо решить волновое уравнение, которому удовлетворяет амплитуда E’(r) электрического поля света, распространяющегося в голограмме
D
E' + k'e
(r)E' = 0 (7)
В соответствии с (6) решение этого уравнения будем искать в виде
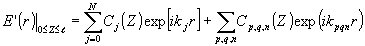 (8) (8)
где функции Cj(Z), Сpqn(Z ) характеризуют изменения по Z интенсивностей и фаз соответствующих плоских световых воля. Так как по предположению |D
e
| << e
0, то функции Cj(Z) и Сpqn(Z ) меняются по Z существенно медленнее, чем стоящие при них в (8) экспоненциальные множители. Это позволяет использовать приближение медленно меняющихся амплитуд.
Первый член в правой части (8) описывает световую волну, содержащую те же плоские компонента, что излучение, распределение плотности энергии которого зарегистрировано в объеме голограммы. Для слагаемых второго члена также могут выполняться условия [kpqn]XoY = [kj]XoY при некоторых р, q, n, j, но, вообще говоря, он описывает "шумовые" световые волны с тангенциальными составляющими волновых векторов, отличными от [kj]XoY (j = 0, 1,…., N). В соответствии с (5) на поверхности голограммы амплитуды световых волн с волновыми векторами [k’]XoY¹
[kj]XoY, j = 0, l,....., N, равны нулю. Возникновение этих волн при Z > 0 связано с рассеянием в голограмме падающих на нее плоских волн. Световые волан, которые возникают в результате рассеяния голограммой волн, соответствующих второму слагаемому в формуле (8), в рамках этой формулы не учитывается. Такая аппроксимация, вообще говоря, применима лишь вблизи поверхности голограммы,
- 166 -
где Cpqn(Z) еще мало отличаются от нуля. Условия применимости приближенной формулы (8) для описания светового поля во всем объеме голограммы выведены в п.2.
Обозначим
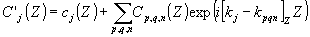 (9) (9)
где суммирование производится по всем р , q, n, для которых [kpqn]XoY = [kj]XoY (j=0,1,...,N), и перепишем (8) в виде
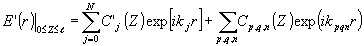 (8) (8)
где второму слагаемому теперь соответствуют только "шумовые" волны. Подстановка (10) в (7) дает после поочередного умножения на еxp[ikjr] и exp[ikpqnr]' и интегрирования по плоскости ХоY систему линейных дифференциальных уравнений для медленно меняющихся амплитуд C’j(Z) и Сℓ¦
g(Z):
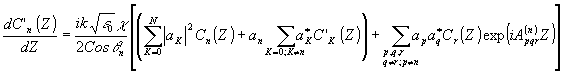 (11а) (11а)
где q
n = Ð
(kn,оZ); суммирование по р, q, r производится для тех индексов, которые удовлетворяют условию:
[kn]XoY = [kr + (kp – kq)]XoY; A(n)pqr = [(kr – kn) – (kq – kp)]Z
- 167 -
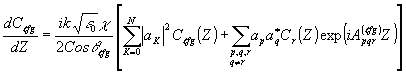 (11 (11
б)
где q
ℓ¦
g = Ð
(k ℓ¦
g,oZ) суммирование по р, q, r производится для индексов, удовлетворяющих условий
[kℓ¦
g]XoY = [kr + (kp – kq)]XoY; A(ℓ¦
g)pqr = [(kr – kℓ¦
g) – (kq – kp)]oZ
Величины A(n)pqr и A(ℓ¦
g)pqr в уравнениях (11а,б) являются проекциями на оZ векторов рассогласования фазовых скоростей плоских световых волн с индексами n и, соответственно, (ℓ,¦
,g) и волны поляризации, наведенной плоским компонентом распространяющегося в голограмме излучения с индексом r в решетке e
pq, созданной интерференцией компонентов записывающего излучения с индексами р и q. Отличие A(n)pqr (A(ℓ¦
g)pqr) от нуля сигнализирует о невыполнении условия Брэгга при рассеянии волны с индексом r в направлении волны с индексом n ((ℓ,¦
,g)) на решетке e
pq.
3. Введем обозначения:
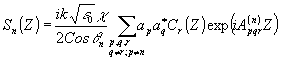 (12a) (12a)
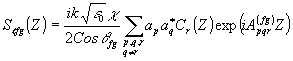 (12 (12
б)
Если экспоненциальные множители при слагаемых Sn(Z) и Sℓfg(Z) быстро осциллирует в пределах толщины голограммы, то их вкладом в С’n(Z) и Cℓfg(Z) можно пренебрегать по сравнению с вкладом других слагаемых в правой, части (11). Исследуем условия, при которых реализуется такой режим преобразования световых волн
- 168 -
в трехмерной голограмме. Из (11а) следует, что указанные условия обеспечивают малость отклонений оператора преобразования световых волн голограммой 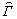 от exp[DÂZ] (где от exp[DÂZ] (где
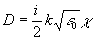 ; ; 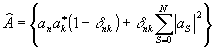
d
nk - символ Кронекера). Так как именно действие оператора на вектор амплитуд плоских компонентов опорной волна b = (0,a ,…., 0, ak+1,…., aN) приводят к его трансформации в вектор амплитуд объектной волны /9/, то малость отклонений 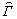 от exp[DÂZ] означает незначительность искажений углового спектра восстановленной волну. С другой стороны, пренебрежение слагаемыми Sℓfg(Z) в уравнениях (11б) эквивалентно пренебрежению "шумовыми" плоскими волнами, обогащающими спектр восстановленной волны плоскими компонентами, отсутствовавшими в зарегистрированном излучении. Оценим вклад Sn(Z) и Sℓfg(Z) в изменения амплитуд распространяющихся в голограмме плоских световых волн в частном случае, когда голограмма безопорная /6,2/. Этот случай представляет значительный самостоятельный интерес (6, 7, 11), а развитая методика исследования применима и к другим схемам трехмерных голограмм. от exp[DÂZ] означает незначительность искажений углового спектра восстановленной волну. С другой стороны, пренебрежение слагаемыми Sℓfg(Z) в уравнениях (11б) эквивалентно пренебрежению "шумовыми" плоскими волнами, обогащающими спектр восстановленной волны плоскими компонентами, отсутствовавшими в зарегистрированном излучении. Оценим вклад Sn(Z) и Sℓfg(Z) в изменения амплитуд распространяющихся в голограмме плоских световых волн в частном случае, когда голограмма безопорная /6,2/. Этот случай представляет значительный самостоятельный интерес (6, 7, 11), а развитая методика исследования применима и к другим схемам трехмерных голограмм.
Предположим, что на безопорную амплитудно-фазовую трехмерную голограмму падает световая волна с соотношением амплитуд плоских компонентов, соответствующим некоторой моде этой голограммы, например, моде с вектором амплитуд плоских составляющих, равным a /6/. Представим вектор амплитуд плоских компонентов волны, распространяющейся при этом в поверхностном слое голограммы, в пределах углового спектра зарегистрированного излучения в виде
C(Z) = a + 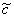 (Z) (Z) (13а)
где
|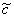 (z)| << |
a|
(13 (z)| << |
a|
(13 б)
|
aj|
»
a
(i = 0, 1,.…., N); фазы aj - независимые случайные величина, равномерно распределенные на отрезке [0,2p
],
- 169 -
Подстановка (13а) в ( 11a) дает с учетом (13б)
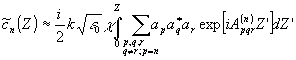
(14а)
где n = 0, 1,...,N; суммирование проводится по индексам р, q, r, удовлетворяющим условиям [kn]XоY = [k r + (k p – k q)] XoY.
Умножим уравнения (11б) на 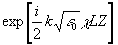 и введем обозначения и введем обозначения 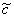 ℓ¦
g(Z)»
Cℓ¦
g(Z) ℓ¦
g(Z)»
Cℓ¦
g(Z)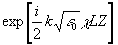 . .
Переходя к одномерной нумерации амплитуд "шумовых" волн и учитывая, что на поверхности голограммы их амплитуды равны нулю, получим

(14б)
где n = N+1, N+2 ,..., Р; суммирование по р, q, r проводится для индексов, удовлетворяющих условиям:
[kn]XoY = [kr + (kp – kq)]XoY
Наша цель состоит в том, чтобы установить, при каких параметрах эксперимента осцилляции функций е xp[iA(n)pqrZ] в (14а,б) обеспечивают подавление "шумовых" и искажающих амплитуды углового спектра преобразованной волны плоских волн. Представим (14а,б) в виде
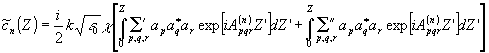 (15) (15)
- 170 -
где å
’ включает в себя суммирование по тройкам индексов (р,q,r), для которых |
A(n)pqr|
Z £
p
; å
” -║- |
A(n)pqr|
Z > p
; n = 0, 1,...., Р.
При вычислении интегралов под знаком å
’ будем пользоваться неравенством 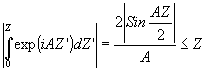 . .
Интегралы под знаком å
” будем оценивать сверху о помощью неравенства 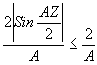 . Это позволит получить с помощью теоремы о дисперсии суммы независимых случайных величин оценку сверху для . Это позволит получить с помощью теоремы о дисперсии суммы независимых случайных величин оценку сверху для 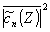 : :
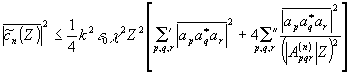 (16) (16)
где черта сверху означает усреднение по ансамблю реализации аргументов а j.
Введем обозначения: G(n) - множество троек индексов (с, d, е), удовлетворяющих условию |
[kn - kc])XoY| = |[kd - ke]XoY|
; S(n)(k)- число троек индексов (с, d, е) Î
G(n), которым соответствуют |
A(n)cde|
Z £
K; S(n)(K + D
K) - число троек индексов (с, d, е) Î
G(n) , для которых Kp
£
|
A(n)cde|
Z £
(K + D
K)p
. С помощью этих обозначений можно преобразовать (16)
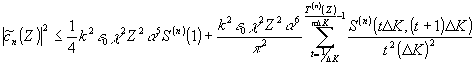 (17a) (17a)
- 171 -
где
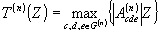 (17) (17)
Найдем оценку сверху S(K) для S(n)(K), справедливую при любом n = 0, 1,...,N. Будем измерять расстояния между точками пространственно-частотной плоскости и углы между соответствующими волновыми векторами. Предположим, что пространственный спектр регистрированного излучения заключен в пределах круга с радиусом ky
/2. Рассмотрим точку n пространственного спектра излучения, распространяющегося в голограмме, соответствующую некоторой точке спектра зарегистрированного излучения. Вклад искажающих волн в амплитуду волны, соответствующей точке n, вообще говоря, зависит от расположения этой точки относительно краев пространственного спектра зарегистрированного излучения. Чтобы не принимать в расчет эту зависимость, будем выбирать точки с пространственного спектра падающей на голограмму волны из круга Фn с цангам в n и радиусом ky
. При этом наряду со всеми рассеивающимися в направлении kn плоскими волнами, лежащими в пределах углового спектра зарегистрированного излучения, мы переберем ряд дополнительных волн. Поэтому полученная в результате оценка S(n)(K) будет существенно завышена.
Зафиксировав некоторую точку с , отстоящую от n на kq
(q
£
y
), построим квадрат Qnc с центром в n и со стороной, параллельной отрезку nс и равной по длине 2ky
(см. рис.1). Выберем некоторую точку частотной плоскости ℓ, лежащую в квадрате Qnc, и точки d’, d", удовлетворяющие условиям;
|[kn – kc]XoY| = |
[kd’ - ke]X оY
|[kn - kc]XoY|
= [kd” - ke]XoY
При этом, т.к. Ð
(kn,kc) = q
, и наклон волновых векторов
- 172 -
плоских компонентов зарегистрированного излучения друг к другу невелик, то Ð
(kd',ke) »
Ð
(kd",ke) »
q
.
Повернем векторы kd' и ke (kd" и ke) вокруг оси, параллельной их разности и проходящей через центр сфера Эвальды, так, чтобы плоскости, содержащей повернутые векторы, принадлежали kc и kn. Обозначим через kd’ и k’e (k'd" и k'e) повернутые
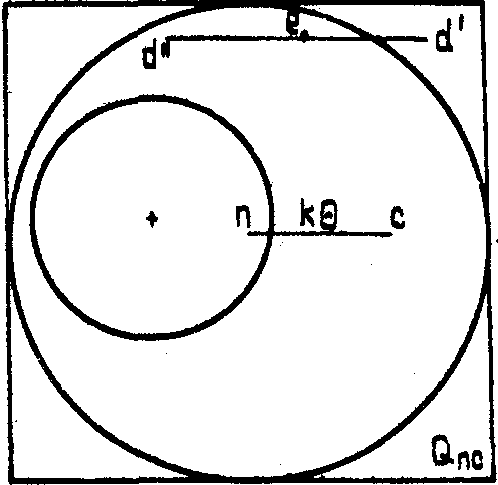
Рис.1. Пространственный спектр распространяющейся в голограмме световой волны, продолженный на вспомогательный квадрат.
векторы.
При зафиксированных n и с легко найти долю точек ее e Î
Qnc. Для которых выполняется, по крайней мере, одно из условий: *)
*) Так как общее число точек е в квадрате Qnc примерно в 6 раз больше числа точек исходного пространственного
- 173 -
|
A(n)cd ”e|
£
p
K/Z (18а)
|
A(n)ced’|
£
p
K/Z (18б)
где (с, d", е), (c, е, d’) Î
G(n). Эта доля определяется относительной длиной частей отрезка [-y
,y
], в которых при выполнении (18а) или (18б) могут быть заключены значения углов Ð
(kn,k’e). Для того, чтобы оценить указанную относительную длину, обозначим x
= Ð
(kn,k’e) и выразим A(n)cd ”e и A(n)ced‘ через x
и q
. В сипу малости расходимости зарегистрированного излучения справедливы следующие аппроксимации:
A(n)cd ”e = [(kc + kd “ – ke) – kn]oZ »
|
k”|
- k (19а)
A(n)ced’ = [(kc + ke – kd’) – kn]oZ »
|
k’|
- k (19б)
где k" = kc + kd " - ke; k’ = kc + ke – kd’.
спектра зарегистрированного излучения, то за эту легкость приходится расплачиваться существенна; дополнительным завышением оценки S(n)(K).
- 174 -
Один из вариантов взаимного расположения векторов, фигурирующих в (19), показан на рис.2.
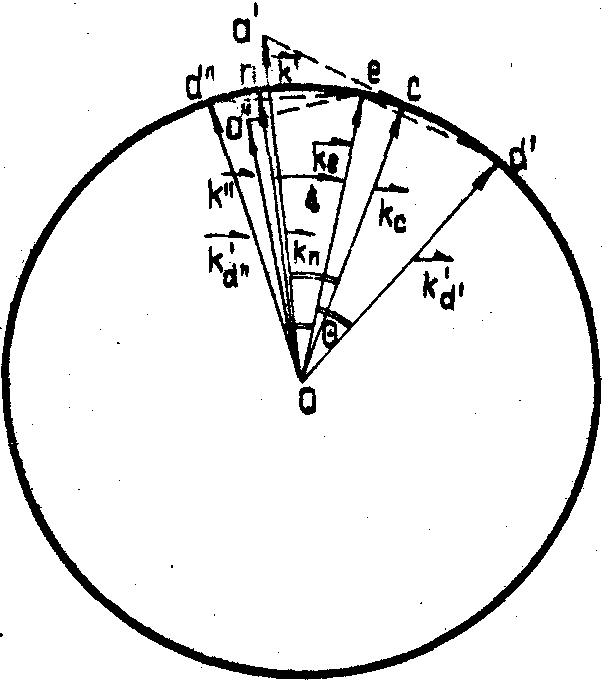
Рис.2. Векторная диаграмма, поясняющая процесс образования "шумовых" и искажающих восстановленную волну плоских волн в объеме голограммы.
Легко доказать, что 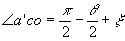 ; ; 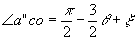 . Поэтому, рассматривая треугольники a'co и а"со, получим: . Поэтому, рассматривая треугольники a'co и а"со, получим:
|
k’|
2 = k2 + k2q
2 – 2k2q
Cos(Ð
a’co) = k2(1 + 2q
x
) (20a)
- 175 -
|
k”|
2 = k2 + k2q
2 – 2k2q
Cos(Ð
a”co) = k2[1 - 2q
(q
- x
)] (20a)
где k = 2p
/l
- волновое число записывающего излучения в регистрирующей среде (радиус сферы Эвальда).
Соотношения (20) останутся справедливыми при любом взаимном расположении векторов kс, kd и ke, если углы, отсчитываемые от kn по часовой стрелке, считать положительными, а против - отрицательными. Вид формул (20) не зависит также от того, с какой стороны плоскости, содержащей рассматриваемые векторы, располагается наблюдатель, т.к. в эти формулы величины x
и q
входят лишь в виде двойных произведений, и при переходе с одной стороны плоскости на другую знаки x
и q
одновременно меняются на противоположные.
Из (20) следует:
|
k'| »
k(1 + q
x
) (21а)
|k"| »
k[1 - q
(q
- x
)] (21б)
Сопоставляя (19) и (21), находим:
A(n)cd ”e »
-kq
(q
- x
) (22a)
A(n)ced’ »
kq
x
(22 б)
- 176 -
Соотношения (22) позволяют установить, что, если q
Î
[0,y
] и x
Î
[-y
,y
], то
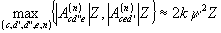 (23) (23)
Этот максимум достигается при q
= y
и x
= -y
, когда
A(n)cd ”e »
-2ky
2
Из (23) следует, что в формуле (17б)
T(n)(Z) £
T(Z) = 2ky
2Z
Соотношения (22) показывают, что условие |A(n)ced’| £
p
k/Z выполняется при
-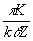 £
x
£ £
x
£
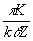 (24а)
а условие |A(n)ced ”| £
p
k/Z - при значениях x
заключенных в пределах
q
- 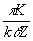 £
x
£
q
+ £
x
£
q
+ 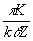 (24б))
Отрезки, задаваемые соотношениями (24), вообще говоря, выходят за рамки отрезка [-y
,y
]. Поэтому суммарная длина e
частей отрезка [-y
,y
], для которых выполняется, по крайней мере одно из условий:
|A(n)ced’| £
p
k/Z; |A(n)ced”| £
p
k/Z
характеризуется не длинами отрезков, задаваемых (24), а длинами их пересечений с [-y
,y
]. С целью упрощения расчетов мы будем
- 177 -
пренебрегать выходом x
, определяемых (24), из [-y
,y
] завышая тем самым оценку суммарной длины e
. Полученная таким способом верхняя оценка относительной суммарной длины частей отрезка [-y
,y
], для которых выполняется одно из условий (18а,б), имеет вид:
e
/2y
£
s
k(q
) £
2p
K/kq
y
Z (25)
С помощью (25) можно найти число точек е квадрата Qnc для которых выполняется, по крайней мере, одно из двух условий (18а,б):
tk(q
) £
GNs
k(q
) (26)
где GN - общее число точек е, лежащих в квадрате Qnc (предполагаем, что исходный пространственный спектр записывающего излучения продолжен на весь квадрат Qnc с сохранением первоначальной плотности точек).
Отрезки, задаваемые условиями (24), вообще говоря, пересекаются. Для точек е, лежащих в области пересечения отрезков; выполняются оба неравенства (18а,б), поэтому число пар (е, d') (e, d"), для которых справедливо хотя бы одно из условий (18а,б), равно удвоенному числу точек е, принадлежащих этой области. Мы, однако, уже учли дважды каждую из таких точек, когда в качестве верхней оценки суммарной длины частей отрезка [-y
,y
], в которых выполняется, по крайней мере, одно из условий (18а,б), взяли полную сумму дайн отрезков, определяемых (20а,б). Поэтому общее число пар (е, d), для которых выполняется (18а) иди (18б), можно оценить сверху числом GNs
k(q
).
Число г(q
)dq
точек с из крута радиуса y
, которым соответствуют волновые векторы, образующие с волновым вектором, соответствующим точке n, углы, лежащие в пределах [q
,q
+ dq
] определяются формулой
- 178 -
r(q
)dq
= 4N·2p
q
dq
/p
y
2 (27)
где 4N/p
y
2 - плотность точек с в круге.
Оценим сверху с помощью (25) - (27) число троен индексов (c,e,d) (с Î
Фn; e Î
Q nc; (c,e,d) Î
G n), которым соответствуют волны поляризации, дающие вклад в световую волну с амплитудой Cn(z) (n = 0, 1 ,...,N) с рассогласованием, меньшим p
K/Z:
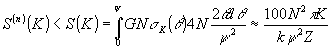 (28) (28)
При p
К = Т(Z) формула (28) сводится к оценке
S (Т) = 200N2
Так как число троек индексов (с ,d,е) Î
G(n) не превышает N2, то из (29) следует, что оценка (28) сильно завышена (по меньшей мере в 200 раз).
Найдем теперь аналогичны/ способом верхнюю оценку для S(n)(К,К+D
К), справедливую при любом n = 0, 1,...N. Из (22) следует, что условие
Kp
£
|
A(n)ced’| £
(K + D
K)p
выполняется при
- 179 -
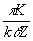 £
x
£ £
x
£
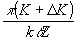
(29а)
и
-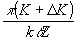 £
x
£
- £
x
£
-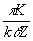 (29б)
а условие Kp
£
|
A(n)ced “| £
(K + D
K)p
- при, значениях , заключенных в пределах
q
+ 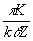 £
x
£
q
+ £
x
£
q
+ 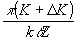 (29в)
и
q
- 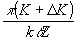 £
x
£
q
- £
x
£
q
- 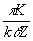 (29г)
Получим с помощью (29) верхнюю оценку s
K,K+D
K относительной суммарной длины частей отрезка [-y
,y
], для которых выполняется одно из условий:
Kp
£
|
A(n)ced‘| £
(K + D
K)p
(30а)
Kp
£
|
A(n)ced “| £
(K + D
K)p
(30 б)
- 180 -
Для этого сложим длины отрезков, задаваемых (29), и поделим результат на 2y
:
s
K,K+D
K(q
) = 2p
D
K/ky
q
Z (31)
Формула (31) позволяет оценить сверху число пар (е, d'), (e, d"), для которых справедливо одно из условий (30) при e Î
Qnc.
tK,K+D
K(q
) = GNs
K,K+D
K (32)
Оценим теперь сверху число троек индексов (c ,е,d)
(с Î
Фn, е Î
Qnс ; (c,e,d) Î
G(n))
которым соответствуют волна поляризации с модулями рассогласования фазовых скоростей относительно световой, лежащими в пределах [Кp
/Z,(К+D
K)p
/Z],
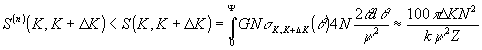 (33) (33)
Подстановка (28) и (33) в (I7a) дает при стремлении D
К
- 181 -
к нулю
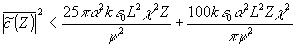 (34) (34)
Из (34) следует верхняя оценка вклада в |Сn(z) |
2 членов вида Sn(Z), неучтенных в /5,6,9/
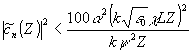 (35) (35)
Эта оценка справедлива в для суммарной интенсивности искажающих волн, порождаемых плоской волной с индексом n при ее рассеянии на решетках с волновыми векторами ke-kd " и kd’-ke. Действительно, фазовая скорость волны поляризация, наводимой световой волной с индексом с в одной из таких решеток и дающей вклад в амплитуду волны с индексом n равна фазовой скорости той волны поляризации, наводимой световой волной с индексом n, которая дает вклад в амплитуду световой волны с индексом с. То есть, как и следовало ожидать, взаимодействие между любыми двумя плоскими компонентами распространяющейся в голограмме световой волны является симметричным. Так как, к тому же, интенсивности этих компонентов по предположению примерно одинакова, то сумма вкладов всех плоских световых волн в интенсивность рассматриваемой равна сумме вкладов данной волны в интенсивности остальных.
Анализ рассуждений, использованных при выводе (35), показывает, что эта оценка остается справедливой, когда на безопорную голограмму падает не мода с вектором амплитуд а = (а 0, а1,. ..., аN), а любая другая ее мода (см. /6/). Если же падающая на голограмму световая волна состоит из нескольких мод, то в силу принципа суперпозиции искажающие волны, порождающие плоскими компонентами различных мод, складываются по амплитуде. Предположим, что голограмма является чисто фазовой и ее считывание
- 182 -
производится частью записывающей волны с числом плоских компонентов, близким к N/2 (это соответствует максимальной дифракционной эффективности голограммы, см. /5/). Тогда, в соответствии с (35), суммарная интенсивность плоских "шумовых" и искажающих объектную волну световых волн оценивается сверху неравенством
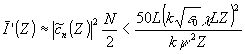 (36) (36)
В пределах приграничного слоя голограммы, в которой' поле восстанавливающей волны можно считать заданным, нарастание интенсивности восстановленной волны с росток Z определяется соотношением
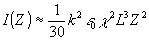 (37) (37)
Формулы (36) и (37) позволяют найти условие подавления искажающих волн в слое голограммы, имеющем малую дифракционную эффективность:
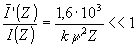 (38) (38)
Наличие множителя 1,6 10 3 в правой части (38) связано с тем, что на всех этапах вывода (38) соответствующие оценки завышались в несколько раз.
Формула (37), а следовательно оценка (38), справедливы при выполнении неравенства k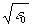 c
LZ << 3. c
LZ << 3.
Подстановка Z »
0,3/k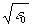 c
L c
L
- 183 -
в (38) дает следующее условие подавления фоновых волн в приграничное слое голограммы
y
2/D
e
' >> 5·103 (39)
где D
e
’ = e
0c
L. При выполнении (39) рассуждения, приведшие к (38), справедливы применительно к тонкому слою голограммы, следующему за приграничным, и т.д. Таким образом, если толщина голограммы ℓ удовлетворяет условию
k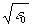 c
Lℓ << 3 c
Lℓ << 3
то для подавления световых волн, не несущих полезную информацию, достаточно выполнения неравенства:
ky
2ℓ >> 1 (40)
Если же k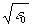 c
Lℓ ³
3, то подавление паразитных волн по сравнению с восстановленной обеспечивается условием (39). c
Lℓ ³
3, то подавление паразитных волн по сравнению с восстановленной обеспечивается условием (39).
В случае амплитудных голограмм в (35) следует заменить c
на |c
|. При освещении такой голограммы пучком, состоящим из плоских компонентов, приращение интенсивности "шумовых" и искажающих волн в слое толщины Z определяется формулой
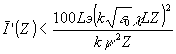 (41) (41)
аналогичной (36), где L’ = N'a
2, N’ ³
N. Приращение интенсивности зарегистрированной волны оценивается при этом выражением (см. /6/):
I(Z) »
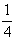 (k (k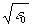 |
c
|
LZ)2L (42) |
c
|
LZ)2L (42)
- 184 -
При N’ »
N условие подавления в тонком слое голограммы световых волн, не несущих полезной информации, имеет вид:
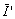 (Z)/I(Z) = 400/(ky
2Z) << 1 (43) (Z)/I(Z) = 400/(ky
2Z) << 1 (43)
Отсюда следуют .условия малости собственных шумов амплитудной трехмерной голограммы, аналогичные (39) и (40):
y
2/D
e
' >> 8·102 (44)
ky
2ℓ >> 4·102 (45)
где D
e
' = e
0|c
|L.
4. Из проведенного рассмотрения следует, что при выполнении (39), (40), (44), (45) паразитные волны нарастают в объеме безопорной трехмерной фазовой (амплитудной) голограммы с ростом Z гораздо медленнее восстановленных волн, и поэтому уравнения (11) с отброшенными членами Sn(Z) адекватно описывают исход экспериментов. Как отмечалось при выводе (38), требования к параметрам эксперимента, налагаемые условиями (39), (40), (44) и (45), являются существенно завышенными. Действительно, вытекающий из усеченных уравнений (11) эффект воспроизведения структуры пространственно неоднородной накачки при вынужденном рассеянии (см. /11,6,7/), наблюдается уже при
y
2/D
e
' ³
4,5, ky
2ℓ »
100 ([11])
Следовательно, ценность соотношений (39), (40), (44) и (45) состоят не в количественной оценке значений y
2 и D
e
', обеспечивающих подавление фоновых волн на выходе голограммы, а в установлении факта, что именно параметры æ=y
2/D
e
' и
- 185 -
m
= ky
2ℓ оказывают решающее влияние на величину' интенсивности этих, мешающих воспроизведении зарегистрированного излучения, волн. Этот результат согласуется с экспериментальными данными, приведенными в /11/. Действительно, тогда как при æ ³
4,5 m
»
100 паразитные волны существенно превышают по интенсивности восстановленную волну.
Полученные в данной работе соотношения (39), (40), (44) и (45) в случае, когда угловой спектр записывающего излучения является равномерным по интенсивности и может быть охарактеризован параметром угловой расходимости, позволяют сформулировать рекомендации по снижений шумов трехмерных голограмм. Эта рекомендация состоит в целесообразности увеличения параметров æ и m
.
Пользуясь развития в работе методом классификации волн поляризации, возбуждаемых распространяющимися в голограмме световыми волнами, и формулами (18) - (34), аналогичные рекомендации можно сформулировать для случая,.когда при записи голограмм использована выделенная по яркости опорная волна, и для других схем записи.
Автор благодарен Ю.Н.Денисюку за поддержку данной работы, Д.И.Стаселько - за ценные обсуждения.
Литература
1. Upatnieks J., Leonard С., Effiency and image contrast of dielectric holograms, Journ.Opt. Soc, Amer., v60, N3., p.297-305, 1970.
2. В.В.Аристов, В.Ш.Шехтман. Свойства трехмерных голограмм, УФН, г.104, № 1, с.51-76, 1971.
3. Forshaw M.R.B., Volume holograms: a survey, Opt, Laser Technol., . v6, N1 , р. 28-33, 1974.
4. Guither R., Kusch S., Schonnagel H., Spolaczy R., Wernicke J. Associativity In volume holography, Opt, Communs., v20., p.56-58, 1977.
5.. В.Г.Сидорович. 0 дифракционной эффективности трехмерных фазовых голограмм, ЖТФ, т.46, № 6, с. 1306-1312, 1976.
6. В.Г.Сидоррвич. Теория преобразования световых полей амплитудными трехмерными голограммами, зарегистрированными в усаливающих средах, Оптика в спектроскопия, т.42, № 4, с.693-699, 1977.
- 186 -
7. В.Г.Сидорович. К теории "бриллюэновского зеркала", ЖTФ, т.46, № 10, с.2168-2174, 1976.
8. Guther R., Kusch S., Ein beitrag zum intermodulationsrauschen in der volumenholographie, Experimentelle Technik der Physik, N2, p.119-141, 1974.
9. В.Г.Сидорович. Расчет дифракционной эффективности трехмерных фазовых голограмм. Оптика и спектроскопия, т.41, № 4, с.507-510, 1976.
10. Heerden Van P.J., The theory of Information storage in Solid state, Appl.Opt., v.2, p.393-400, 1963.
11. Б.Я.Зельдович, В.И.Поповичев, В.В.Рагульский, Ф.С.Файзуллов. О связи между волновыми фронтами отраженного и возбуждающего света при вынужденном рассеянии Мандельштама-Бриллюэна, Письма в ЖЭТФ, т.15, № 3, с.160-164, 1972.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

