ИНФОРМАЦИОННЫЕ СВОЙСТВА ЛИНЕЙНЫХ ОПТИЧЕСКИХ СИСТЕМ, ФОРМИРУЮЩИХ ИЗОБРАЖЕНИЕ

В.Н.Курашов

Методом разложения случайного волнового поля, формирующего ансамбль изображений, в ряд с некоррелированными коэффициентами получен рад информационных характеристик линейной оптической системы. Строго определено понятие числа эффективно возбуждаемых степеней свободы изображения для произвольной пространственной когерентности поля. Приведены количественные результаты для апертур, состоящих из системы точечных элементов.

Формирование изображения в произвольной оптической системе представляет собой информационный процесс, в котором входные и выходные сигналы описываются функциями пространственных координат, заданными на конечной апертуре. Естественно поэтому применение критериев теории информации для оценки качества изображающих систем, строгого определения таких ее характеристик, как разрешающая сила, информационная эффективность, уровень шума и т.п. Первые pаботы в этом направлении, выполненные Торальдо-ди-Франсия /1,2/ помогла осознать тот факт, что дифракционный предел разрешения, установленный Релеем и считавшийся абсолютным теоретическим пределом точности оптического изображения, на самом деле является лишь техническим и может быть превзойден в идеальной оптической системе.

Единственное, что действительно ограничивает пропускную способность - это шум, как и в любом информационном канале. С другой стороны, приобретает строгий физический смысл понятие степени свободы изображения /3/, т.е. такого его элемента, линейно независимая суперпозиция которых обеспечивает произвольно малое различие между изображением

- 167 -

и оригиналом. Произведение полосы пространственных частот оптической системы W на площадь выходной апертуры S, называемая числом Шеннона, служит грубой оценкой необходимого количества этих элементов. Качественный характер подобной оценки, основанной на теореме отсчетов Котельникова, подчеркивается двумя обстоятельствами: во-первых, из предложения о финитности частотного изображения следует, что распределение поля на апертуре - аналитическая функция, которая может быть определена во всем пространстве, если известна в конечной его области /4,5/; во-вторых, корреляции в ансамбле изображаемых объектов приводят к появлении статистических связей между отдельными отсчетами, так что последние нельзя считать линейно не зависимыми. Строгий математический анализ этой проблемы для детерминированных сигналов /3,6-9/ показал, что понятие степени свободы поля в линейной оптической системе является вполне корректным, а ограничение из числа - оправданным в практическом смысле. С помощью такого подхода были рассмотрены проблемы восстановления изображения /10/ определена разрешающая сила оптического устройства в присутствии аддитивных шумов /11/, установлена связь оптических критерием качества с теорией информации /12/. Вместе с тем, оказалось, что детерминистический подход не достаточен для полного описания информационных характеристик системы, формирующей изображение. В частности, до сих пор остается спорным вопрос о соотношении пропускных способностей при когерентном и некогерентном освещении объекта. Впервые эта задача рассматривалась в paботе /3/. Анализируя свойства кольцевой апертуры, автор сделал вывод, что для когерентного поля число степеней свободы практически совпадает с числом Шеннона одномерной щели той же длины, тогда как при некогерентном освещении физическую площадь апертуры следует заменить площадью ее автокорреляционной функции, т.е. фактически площадью всего диска,ограниченного щелью. В заметке Вальтера /13/ этот результат опровергался из соображений нормировки корреляционной функции выходного сигнала. Наконец, в работе /14/ эта проблема рассматривалась для апертуры, состояуей из точечных элементов. Полученные результаты фактически согласуются с /3/, что, по мнению авторов, заходит подтверждение в известном парадоксе креста Милса /15/. Именно, кольцевая или крестообразная апертура, состоявшая

- 168 -

из N - элементов, позволяет наблюдать в изображении ~ N² разрешимых точек. При некогерентном облучении это соответствует N² независимым отсчетам, тогда как для когерентного поля взаимные корреляции снижают это число до N. Не касаясь деталей доказательства, можно заметить, что оно противоречит принципу аддитивности информации. Действительно, прибавление единственного дополнительного отсчета при увеличении числа элементов апертуры на единицу должно сопровождаться пропорциональным, а не квадратичным возрастанием количества информации.

Трудности решения подобных проблем в рамках теории линейных преобразований детерминированных сигналов связаны как раз с обобщением понятия степени свободы изображения на стохастические поля. Строгий подход должен основываться на последовательном применении теоретико-информационных методов, определяющих любой информационный процесс как преобразование случайного сигнала. Оказывается, что это позволяет установить эффективные количественные критерии качества оптических изображающих систем, в том числе и представление об эффективных степенях свободы изображения.

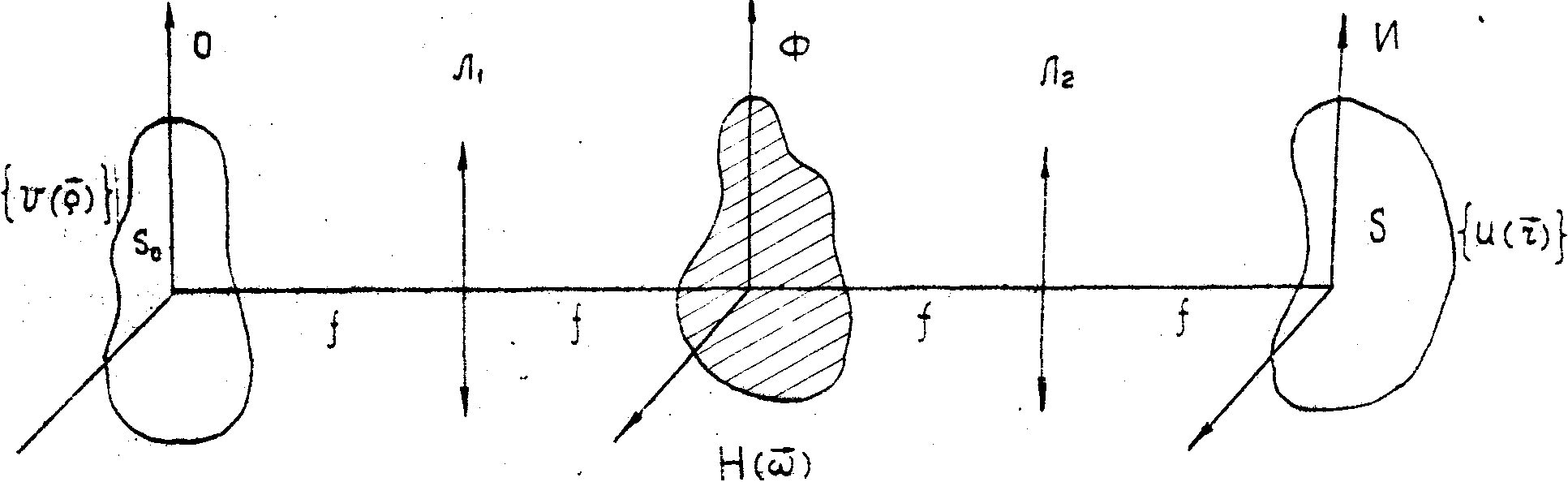
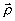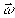Рассмотрим оптическую систему, представленную на рис.1а. В объектной плоскости 0 задано поле v(), ограниченное апертурой S₀ и являющееся реализацией некоторого двумерного случайного процесса. В плоскости Фурье Ф линзой Л₁ формируется спектр пространственных частот, преобразуемых транспарантом с комплексным пропусканием H(). Изображение u(), восстанавливаемое линзой Л₂, формируется на апертуре S выходкой плоскости U. Эквивалентная схема такого оптического канала доказана на рис.1б. Ключи К₁ и К₂ выполняют операцию двумерного стробирования, т.е. ограничения случайных функций v(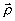) и u() конечными апертурами. Оператор 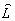определяет линейное преобразование поля в системе с импульсным откликом (функцией рассеяния точки h(,):

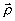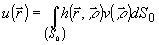(1)

- 169 -

а)

б)

Рис.1. Оптическая система формирования изображения и ее эквивалентная хема.

- 170 -

Наконец, как во входной, так и в выходной плоскостях возможно появление аддитивных шумов n₁(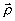) и n₂(). Основная информационная характеристика канала - взаимная информация между сигналами v(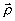) и u():

I(u,v) = H(u) - H(u | v) (2)

где Н (u) - энтропия ансамбля изображений, Н(u | v) - его условная энтропия для фиксированной реализации объектного поля. Как обычно (см.напр. /16/), для определения этих величин удобно использовать ортогональное разложение случайных сигналов, т.е. представление их в виде

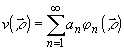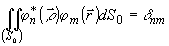; (3)

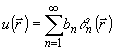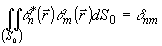; (4)

где j _n(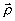) Î L₂(S₀) и q _n() Î L₂(S). При этом все интересующие нас величины описываются совместными распределениями вероятностей коэффициентов разложения p({a_n}¥ ₁;{b_n}¥ ₁). В частности,

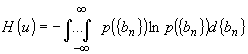(5)

и аналогично для Н(u | v). Любая реализация u() представляется теперь счетным множеством коэффициентов {b_n}¥ ₁, каждый из которых определяет относительную величину вклада соответствующей "модовой" функции q _n() р общую энергию изображения.

- 171 -

О классе функций, в котором любая из них может быть определена N-числами, говорят, что он имеет N степеней свободы. (Это верно, строго говоря, для множества действительных чисел. Хотя коэффициенты ортогональных разложений (3) и (4) - комплексны, мы в дальнейшем для простоты будем сохранять такую терминологию, понимая под степенью свободы комплексную амплитуду разложения). Поскольку множество q _n() не ограничено, пространство представления изображений - бесконечномерно, а, следовательно, число степеней свободы в общем случае не ограничено. Однако, всегда можно найти приближенную проекцию случайного процесса u() на конечномерный базис L₂(S). Если ошибка такой аппроксимации не превышает e , имеет смысл, очевидно, говорить о степенях свободы, эффективно участвующих в формировании изображения при заданном уровне ошибки. Естественно, что при этом подразумевается оптимальность выбранного базиса, т.е. отсутствие статистических связей между различными элементами разложения. Таким образом, будем считать, что изображение содержит Nd эффективных степеней свободы, если

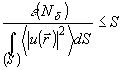(6)

где d - заданный уровень среднеквадратичной ошибки Nd -мерной аппроксимации разложения случайного процесса u() в ряд с некоррелированными коэффициентами:

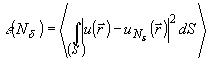(7)

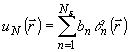(8)

- 172 -

<b^*_nb_n> = l _{nd nm} (9)

Для гауссовых случайных полей последнее утверждение эквивалентно условию статистической независимости b_n, так что

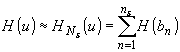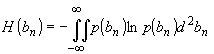; (10)

Интегрирование в (10) проводится по всей комплексной плоскости , на которой определены значения амплитуды модовой функции b_n.

Покажем, прежде всего, что такое ортогональное разложение существует. Используя соотношение полноты

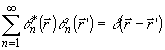; (11)

получим из равенства (9), умножая его на q _m() и суммируя по m:

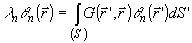(12)

где

G(',) = G^*(,') = <u^*(')u()> (13)

- автокорреляционная функция поля на выходе канала. Таким образом, ряд с некоррелированными коэффициентами для случайного процесса может быть получен при использовании собственных функций интегрального оператора с ядром (13). Это утверждение составляет содержание теоремы Карунена-Лоэва /17/. Из свойств корреляционной функции следует, что этот оператор - самосопряженный

- 173 -

неотрицательно-определенный оператор типа Гильберта-Шмидта, для которого справедливы следующие утверждения /18,19/:

1) собственные значения l _n образуют счетную, квадратично-суммируемую последовательность действительных неотрицательных чисел. Каждое l _n имеет конечную кратность вырождения, так что все собственные функции q _n() могут быть ортонормированы,

2) базис {q _n()} оптимален в смысле аппроксимации (8), т.е. среднеквадратичная ошибка e (Nd ) минимальна на нем, причем

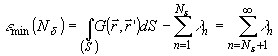(14)

где все l _n расположены в невозрастающем порядке. Равенство (14) позволяет не только оценить величину ошибки конечномерного представления изображения u(), но и выигрыш от учета дополнительных степеней свободы.

Аналогичное разложение возможно, очевидно, и для ансамбля объектов v(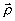), однако все коэффициенты b_n оказываются в этом случае статистически связанными с a_m. Действительно, определяя отклик

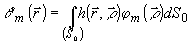(15)

найдем из (1), (3) и (4):

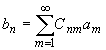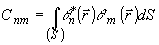; (16)

Матрица C_nm, вообще говоря, недиагоналъна, т.к. q '_m() не есть функция множества {q _m}. Отсюда

<a^*_mb_n> = C_nm ¹ d _nmC_nm (17)

- 174 -

и условная энтропия не представима в виде (10).

Можно попытаться использовать другой подход, требуя, чтобы функции отклика q '_m() на базисные входные сигналы j '_m(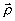) образовывали полную ортогональную на L₂(S) систему. Естественно назвать такие функции модовыми функциями канала. Тогда, повторяя рассуждения, использованные при выводе (12), найдем, что функции j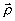 '_n() и q '_n() удовлетворяют аналогичному уравнению, но, соответственно, для ядер

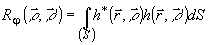(18)

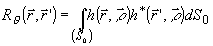(19)

и одинаковых собственных значений l '_n. Функции Rq и Rj , как нетрудно убедиться, обладают теми же свойствами, что и G(,'), так что все утверждения, сделанные выше относительно решения уравнения (12), остаются справедливыми и здесь. Разложение по функциям j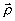 '_n() и q '_n() позволяет описать оптическую изображающую систему последовательностью линейных одномерных каналов со статистически связанными входами и выходами. Действительно , в этом случае C_nm=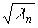d _nm, так что процесс образования изображения формально сводится к параллельной обработке множества коэффициентов {a_n} в простом перемножающем устройстве:

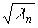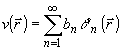b_n =a_n; (20)

Можно показать также, что обратное преобразование - "восстановление" изображения - определяется линейной операцией с импульсным откликом

- 175 -

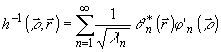(21)

Фильтр (21) эквивалентен параллельной обработке коэффициентов b_n аналогичной (20):

a_n = b_n / 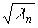; 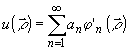(22)

которая однозначно определяет входной сигнал в отсутствии, шума. Эквивалентная схема формирования изображения и его восстановления показана на рис.2. Очевидно, однако, что такая процедура представления оптической системы в виде совокупности параллельных одномерных каналов, хотя и отличается особой простотой, неоптимальна, поскольку

<a^*_na_m> ¹ a _{nd nm}; <b^*_nb_m> ¹ b _{nd nm}; (23)

и, следовательно, множество коэффициентов {b_n} информационно избыточно. Исключение составляет ансамбль объектов, образующих белый гауссов шум, для которого <a^*_na_m> = d _nm при любом ортогональном разложении. Отметим, что в этом случае представление выходного сигнала (20) совпадает с (4), поскольку

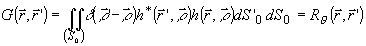(24)

Таким образом, модовые функции оптической системы q '_n() совдадают в этом случае м базисными степенями свобода изображения q _n().

- 176 -

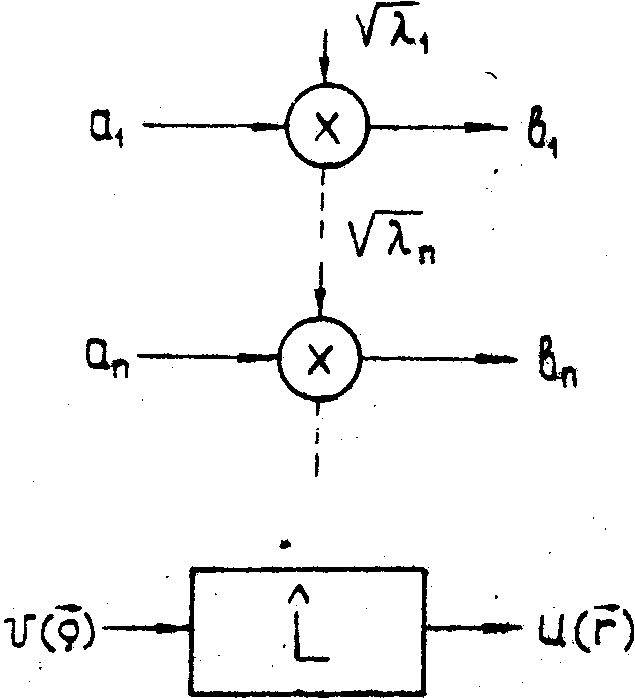
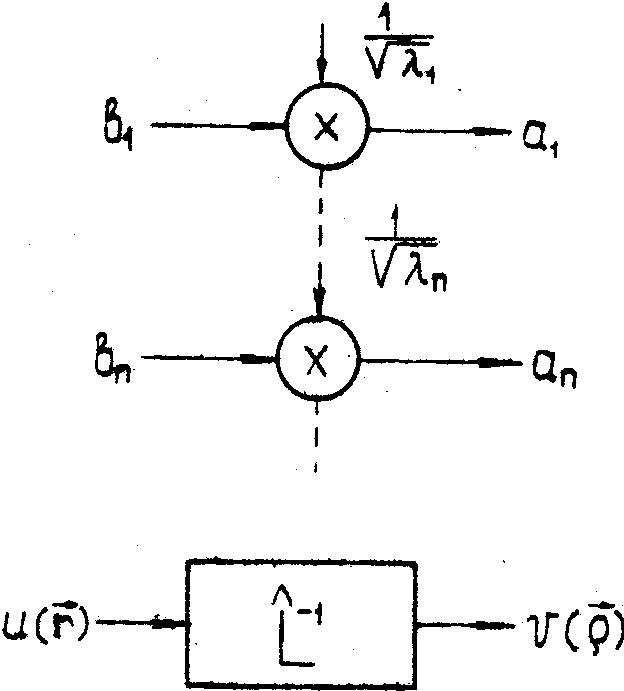
Рис.2. Эквивалентное представление формирования и восстановления изображения совокупностью одномерных каналов.

- 177 -

Заметим, что соотношение (24) есть просто аналог теоремы Ван-Циттерта-Цернике для обобщенного линейного оптического канала. Статистическая независимость одномерных каналов (20) и (22) позволяет легко определить как информационные характеристики изображения на выходе оптической системы, так и ее эффективность. Ввиду этого, при описании фильтрации частично когерентных полей используют так называемый метод приведения небелого гауссова шума к белому /16/ с помощью введения эквивалентного фильтра, образующего случайный процесс с заданной спектральной плотностью. Мы в дальнейшем будем предполагать, что такая операция выполнена, т.е. входной ансамбль объектов пространственно некогерентен.

Приведенный выше общий анализ позволяет выделить два фактора, определяющие информационную эффективность линейной оптической системы : первый из них - это число степеней свободы изображения, т.е. количество модовых функций, участвующих в его обработке; второй - уровень шума в каждом из совокупности эквивалентных одномерных каналов. Мы рассмотрим сейчас роль первого фактора, т.е. определим число степеней свободы в формируемом изображении при различной степени когерентности поля на выходе канала или, что равнозначно, при различной полосе пропускания эквивалентного формирующего фильтра. аддитивными шумами будем пренебрегать, считая систему идеальной. Для простоты анализа будет использоваться модель апертуры, состоящей из N точечных элементов, аналогичную рассмотренной в /9,14,20,21/. Представим функцию пропускания системы в виде

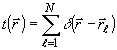(25)

так что поле u() на апертуре

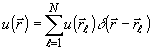(26)

- 178 -

Чтобы избежать определенных трудностей, возникающих при использовании ядер, содержащих обобщенные функции, будем считать, что u() пропускается через линейный фильтр, импульсный отклик которого g(,') отличен от нуля в малой окрестности точки - '= 0, где u() существенно не изменяется. Учитывая сглаживающее воздействие фильтра, запишем

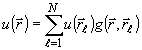(27)

так что

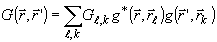(28)

где G_ℓ,k = <u^*(_ℓ)u(_k)> - элементы корреляционной матрицы излучения на апертуре. Ядро (28) вырождено и, следовательно, уравнение (12) легко решается сведением к линейной алгебраической системе. Обозначая

(29)

найдем из (12):

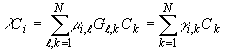(30)

где

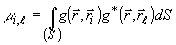(31)

- 179 -

а матрица 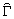= {g _ik} есть произведение матриц 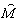= {m _ik} и G = {G_ik}. Собственные значения l определяются из секулярного уравнения

det [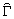 - l ·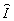] = 0 (32)

где 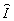- единичная матрица. Поскольку матрица 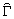неотрицательно определена, l _n образуют последовательность действительных неотрицательных чисел, каждому из которых соответствует базисная функция

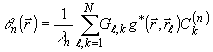(33)

где С⁽ⁿ⁾_k - решение уравнения (30) для l = l _n. Этот вывод справедлив для произвольной геометрии. Таким образом, система N точечных элементов формирует изображение, состоящее из базисных функций, независимо от геометрии апертуры и корреляционных свойств поля u(). Однако в энергетическом смысле не все они одинаково значимы, так что, вообще говоря, Nd £ N. Максимальное число эффективно возбуждаемых степеней свободы соответствует некогерентному ансамблю u(). Действительно, пусть перекрытие функций g(,_ℓ) незначительно, так что m _iℓ » d _iℓ и g _iℓ = G_iℓ. Тогда, полагая G_iℓ = J_{0d iℓ}, найдем из (32),что собственное значение l = J₀ оказывается N-кратно вырожденным, так что все степени свободы одинаково эффективны и Nd » N. Наоборот, для когерентного излучения G_iℓ = J₀ и, как нетрудно убедиться, l ₁ = NJ₀, l ₂ = l ₃ = … = l _N = 0. Вся энергия излучения в этом случае сосредоточена практически в одной модовой функции. Физически это означает, что в когерентном ансамбле для полной идентификации изображения достаточно определения одной комплексной амплитуды C₁. В промежуточном случае частично когерентного поля Nd зависит, очевидно, как от площади когерентности, так и от геометрия апертуры.

- 180 -

Рассмотрим, например, формирование изображения линейной апертурой, состоящей из точечных элементов, расположенных на одинаковом расстоянии друг от друга вдоль оси æ. Пусть, кроме того, поле u() экспоненциально коррелировано, т.е.

С(х,х') = J₀·ехр[-| x – x'| /x₀] (34)

где х₀ - радиус когерентности. Элементы корреляционной матрицы имеют вид:

G_ℓ,k = J₀·g| ^{ℓ - k|} ; g = ехр(-d₀/x₀) (35)

где d₀ - расстояние между соседними элементами. Для решения уравнения (32) заметим, что линейное преобразование переменных в системе (30) позволяет свести матрицу 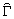- l ·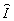 к якобиевой с отличными от нуля элементами:

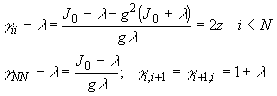(36)

Рассматривая далее det(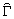 - l ·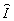) = D_N(z) как функцию параметра z, нетрудно убедиться, что

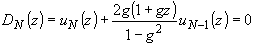(37)

- 181 -

где u_n(z) - полином Чебышова второго рода;

u(Cosæ) = Sin(N + 1)æ / Sinæ; Z = Cosæ (38)

N неиквивалентных корней уравнения (34) æ_n(n = 0,1 …, N-1) лежат в интервалах (n+1')p £ Næ_ℓ £ np , и каждому из них соответствует собственное значение

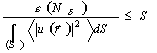(39)

причем l _max = l ₀ » J₀(1+g)/(1-g), l _min = l _N-1 » J₀(1-g)/(1+g). Для опенки эффективного числа степеней свободы положим N >> 1, так что суммирование в (14) можно заменить интегрированием по æ. Тогда нетрудно показать, что

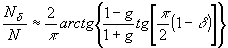(40)

Зависимости Nd от корреляционного параметра а. для нескольких значений g приведены на рис.3, который дает представление о числе степеней свободы,эффективно участвующих в формировании изображения.

В заключение остановимся кратко на влиянии геометрического фактора на величину Nd . Можно полагать, что увеличение средней корреляции поля для всех пар элементов (i,k) сопровождается уменьшением Nd . Это означает, что при фиксированном радиусе когерентности x₀ число степеней свободу оказывается тем меньше, чем компактнее расположены элементы на апертуре. Так, например, для кольцевой апертуры оно меньше, чем для линейной той же длины.

- 182 -

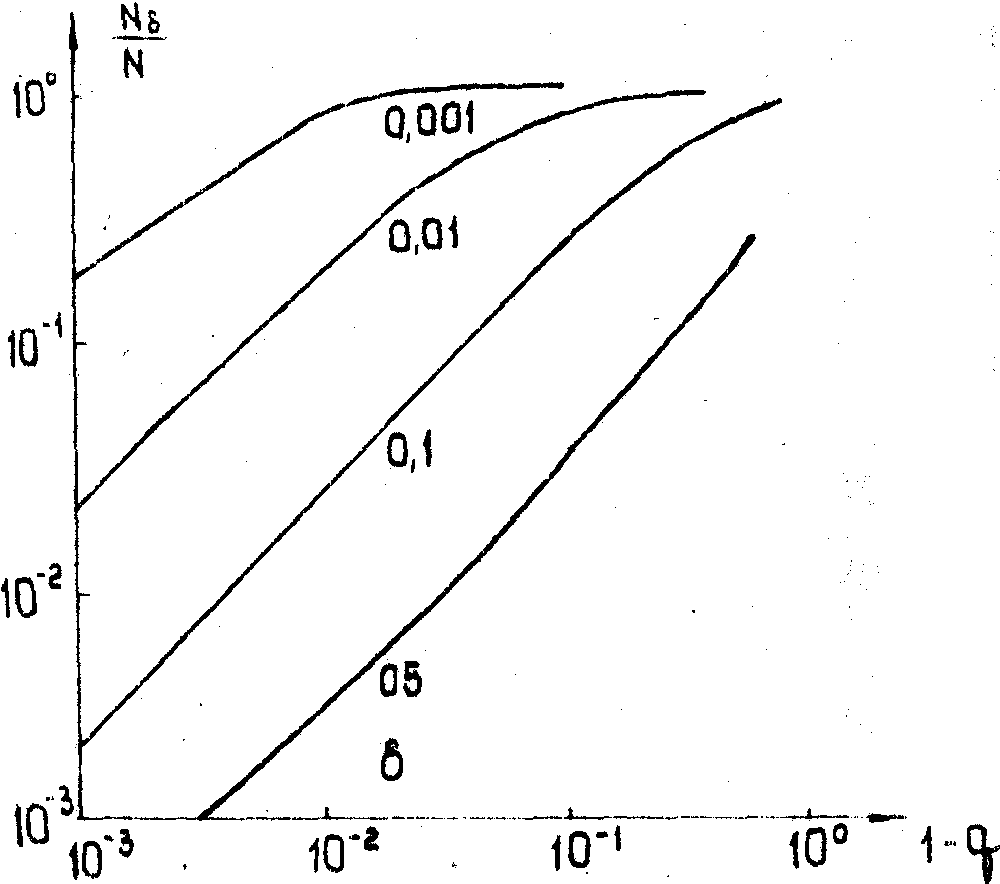
Рис.3. Эффективное число степеней свободы в изображении, формируемом точечной апертурой.

- 183 -

Упомянутый выше парадокс креста Миллас /15/ на первый взгляд противоречит атому выводу. Так, например, для кольцевого интерферометра Уайльда с апертурой из 96 элементов было получено изображение, состоящее из ~ 3000 разрешимых точек /22/. Однако, на самом деле, противоречие здесь отсутствует. Дело в том, что определение числа разрешаемых элементов (в смысле критерия Релея) и числа степеней свободы изображения не эквивалентны, поскольку отдельные точки могут быть оптически разрешимыми, но статистически связанными между собой. Иными словами, в информационном смысле эти критерии имеют существенно различное значение, и только второй из них отражает пропускную способность оптической системы.

Литература

1. G.Toraldo di Francia, Nuovo Cimenta , Suppl, 9, 426, 1952.

2. G.Toraldo di Francia, Opt.Soc.Amer., 45, 497, 1955.

3. G.Toraldo di Francia, Opt.Soc,Amer., 59, 799, 1969,

4. H.Woltez, Progress in Optics, ed E.Wolf, 1, 157, North -Holland Publ, Co, Amsterdam, 1961.

5. Я.И.Хурчин, В.П.Яковлев.. Методы теорий целых функций в радиофизике, теория связи и оптике, Физматгиз, М., 1962.

6. A.Walther, J.Opt.Soc.Amer., 57, 639, 1967.

7. B.Trieden Ray, Optica Acta 16, 795, 1969.

8. F.Gori, G.Guattari, Opt. Communs, 7, 163, 1973.

9. F.Gori, G.Guattari, J.Opt.Sоc.Amer., 64, 453, 1974.

10. G.Buck, J.Gustincle, IEEE Trans., AP-15, 376, 1967.

11. C.Rushforth, R.Harris, J.Opt.Soc.Amer., 58, 535, 1968.

12. N.Bershad, J.Opt.Soc.Amer., 59, 157, 1969.

13. A.Walther, J.Qpt.Soc.Amer., 60, 141, 1970.

14. F.Gori, G.Guattari, J.Opt.Soc.Amеr., 61, 36, 1971.

- 184 -

15. B.Mills, A.Little, Australian, Phys, 6, 272, 1953.

16. Р.Галлагер. Теория информации и надежная связь, Сов. радио, М.,1974.

17. М.Лоэв. Теория вероятностей, ИЛ, М., 1962.

18. В.Лавенпорт, В.Рут. Введение в теорию случайных сигналов и шумов, ИЛ, М., I960.

19. Л.Френкс, Теория сигналов. Сов. радио, М., 1974.

20. М.Борн, Э.Вольф. Основы оптики. Наука, М., 1970.

21. F.Gori, G.Guattari, Optica Acta, 22, 93, 1975,

22. J.Wild. Ргaс.Ray.Soc., А286, 499, 1965.