КВАНТОВЫЕ
ЭФФЕКТЫ В ЛИНЕЙНЫХ ОПТИЧЕСКИХ КАНАЛАХ
В.Н.Курашов
Развит
формализм квантового описания информационных свойств линейных
пространственных оптических систем. Предложен метод кодового
разложения оператора положительно-частотной части напряженности
электрического поля в плоскости изображения в ряд с некоррелированными
операторами-амплитудами. Метод иллюстрируется вычислением
предельной Информационной емкости квантового ансамбля экспоненциально-коррелированных
полей на одномерной апертуре для детектора в виде идеального
счетчика фотонов.
Использование
разложения Карунена-Лоэна для анализа линейных оптических систем /1/ дает строгое
теоретико-информационное описание процесса формирования и обработки изображения,
позволяет ввести удобные критерии пропускной способности и разрешающей силы
оптического устройства. Вместе с тем, такой подход является существенно классическим,
поскольку он определяет пространственную обработку информации в когерентном
оптическом канале как преобразование случайного волнового поля 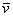 (
( ).
Квантовые эффекты в системах подобного типа, влияние которых неоднократно обсуждалось
(см., напр., /2-5/), изучались в основном лишь для одномерных временных каналов,
либо на феноменологических моделях изображения с независимыми отсчетами, образуемыми
некогерентно излучающими участками объекта /6/. Ниже мы рассмотрим квантовое
обобщение представлений о степенях свободы изображения для поля произвольной
когерентности, позволяющее более строго определить основные оптические характеристики
изображающей системы с учетом кванговомеханических закономерностей.
).
Квантовые эффекты в системах подобного типа, влияние которых неоднократно обсуждалось
(см., напр., /2-5/), изучались в основном лишь для одномерных временных каналов,
либо на феноменологических моделях изображения с независимыми отсчетами, образуемыми
некогерентно излучающими участками объекта /6/. Ниже мы рассмотрим квантовое
обобщение представлений о степенях свободы изображения для поля произвольной
когерентности, позволяющее более строго определить основные оптические характеристики
изображающей системы с учетом кванговомеханических закономерностей.
Напомним
вначале наиболее существенные положения квантовой теории
оптической когерентности и детектирования фотонов, развитые
-
153 -
в работах
Глаубера /7/ и Сударшана /8/. Если рассмотреть взаимодействие электромагнитного
поля с атомной системой в области ħw >> 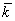 Т
можно убедиться, что переходы с излучением и 'поглощением энергии играют различную
роль. Грубо говоря, вклад в наблюдаемые величины обусловлен лишь той часть”
взаимодействия, которая связана с переходами атома из основного состояния в
возбужденное. Амплитуда вероятности перехода системы поле + детектор имеет вид:
Т
можно убедиться, что переходы с излучением и 'поглощением энергии играют различную
роль. Грубо говоря, вклад в наблюдаемые величины обусловлен лишь той часть”
взаимодействия, которая связана с переходами атома из основного состояния в
возбужденное. Амплитуда вероятности перехода системы поле + детектор имеет вид:
A(a,¦
® b,g) ~ <b,¦
| 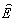
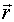 |
ag> = <¦ |
|
ag> = <¦ |
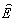 |
g><b|
|
g><b| 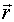 |
a> (1)
|
a> (1)
Здесь
индекса (a,b) относятся к состояния детектора, (¦ ,g)
- поля излучения,
Hi
= -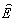
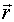 - энергия взаимодействия в дипольном приближении,
- энергия взаимодействия в дипольном приближении,
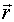 - оператор дипольного момента;
- оператор дипольного момента;
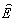 - напряженность электрического поля.
- напряженность электрического поля.
Поскольку
дипольный момент атома осциллирует во времени как
exp[i(Wb
– Wa)t/ħ]
где Wab
— анергия соответствующих уровней, очевидно, что петлевой вклад в А дают лишь
те компоненты 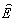 , которые
имеют временную зависимость:
, которые
имеют временную зависимость:
exp(-iw
t); w »
Eb - Ea ³ 0
Следовательно,
можно разделить оператор напряженности электрического поля
на положительно- и отрицательно-частотные части
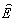 (
( ,t)
=
,t)
= 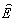 (+)(
(+)( ,t)
+
,t)
+ 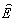 (-)(
(-)( ,t) (2)
,t) (2)
и
считать, что
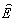 (+)(
(+)( ,t)
~ exp(-iw t)
,t)
~ exp(-iw t)
-
154 -
ответственна
за наблюдаемые взаимодействия детектора с полем. В интерференционных
экспериментах это приводит к необходимости рассматривать
корреляции вида:
GN( ,t;
,t; ',t')
= <
',t')
= <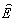 (-)(
(-)( ,t)
,t)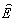 (+)(
(+)( ',t')> (3)
',t')> (3)
где функции
GN носят название нормально упорядоченных, поскольку они содержат
произведения операторов рождения и уничтожения фотонов в нормальном порядке.
Усреднение в (3) подразумевает необходимость учета статистических флуктуации
в квантовомехеническом ансамбле полей, описываемом матрицей плотности 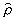 .
Выбор конкретного представления для
.
Выбор конкретного представления для 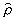 зависит от круга решаемых задач. В оптической теории наиболее удобным оказался
подход, основанный на так называемых когерентных состояниях, для которых
зависит от круга решаемых задач. В оптической теории наиболее удобным оказался
подход, основанный на так называемых когерентных состояниях, для которых
GN( ,t;
,t; ',t')
',t')
факторизуется:
GN( ,t;
,t; ',t')
= e *(
',t')
= e *( ,t)e
(
,t)e
( ',t') (4)
',t') (4)
Не останавливаясь
подробно на свойствах таких состояний, изложение которых можно найти в /7-8/,
отметим лишь, что они являются собственными функциями 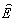 (+)(
(+)( ,t):
,t):
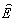 (+)(
(+)( ,t)
| e
> = e (
,t)
| e
> = e ( ,t)
| e
> (5)
,t)
| e
> (5)
образуют
полную неортогональиую систему и в физическом отношении
англогичны классическим волновым пакетам с фиксированной
амплитудой и фазой. Хотя применение неортогональных функций
кажется на первый взгляд достаточно неудобным, оно сильно
упрощает расчету благодаря специальной конструкция измеряемых
в квантовой оптике величин. Действительно, для всех нормально
упорядоченных операторов
-
155 -
полевые
переменные при усреднении на таких состояниях могут быть
просто заменены своими собственными значениями. Используя
когерентное представление матрицы плотности, мы можем поэтому
свести вычисление средних к простому интегрированию на комплексной
плоскости.
Как и в
классической теории нам, далее, удобно перейти от непрерывных переменных 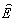 (+)(
(+)( ,t)
к дискретному набору операторов. Обычно это достигается для свободного электромагнитного
поля введением определенных граничных условий. Аналогичный метод используется
и для описания процедуры квантовомеханических измерений полевых переменных.
Если предположить, что детектор удавливает энергию излучения, поступающую в
некоторую полость с абсолютно проводящими стенками, а затем производит необходимые
измерения, можно разложить
,t)
к дискретному набору операторов. Обычно это достигается для свободного электромагнитного
поля введением определенных граничных условий. Аналогичный метод используется
и для описания процедуры квантовомеханических измерений полевых переменных.
Если предположить, что детектор удавливает энергию излучения, поступающую в
некоторую полость с абсолютно проводящими стенками, а затем производит необходимые
измерения, можно разложить 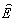 (+)(
(+)( ,t)
по кодовым функциям этой полости, удовлетворяющим уравнению Гельмгольца и граничным
условиям, определяемым геометрией детектора. Более реалистичной, однако, кажется
модель, соответствующая заданию поля на апертуре детектора. В этом случае для
определения собственных решений уравнения дифракции рассматриваются плоские
граничные условия. Мы в дальнейшем используем именно этот подход и представим
,t)
по кодовым функциям этой полости, удовлетворяющим уравнению Гельмгольца и граничным
условиям, определяемым геометрией детектора. Более реалистичной, однако, кажется
модель, соответствующая заданию поля на апертуре детектора. В этом случае для
определения собственных решений уравнения дифракции рассматриваются плоские
граничные условия. Мы в дальнейшем используем именно этот подход и представим
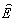 (+)(
(+)( ,t)
в виде:
,t)
в виде:
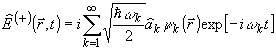 (6)
(6)
где 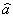 k
- оператор уничтожения фотонов k-того полевого осциллятора; y k(
k
- оператор уничтожения фотонов k-того полевого осциллятора; y k( )
- собственные функции уравнения Гельмгольца, определяемые граничными условиями
на конечной апертуре S и образующие на ней полную ортонормированную систему.
В дальнейшем ограничимся скалярным монохроматическим приближением, полагая
)
- собственные функции уравнения Гельмгольца, определяемые граничными условиями
на конечной апертуре S и образующие на ней полную ортонормированную систему.
В дальнейшем ограничимся скалярным монохроматическим приближением, полагая
w
k
= w = const
что
позволяет опустить временную зависимость в (6) и рассматривать
лишь пространственные преобразования сигнала.
Нетрудно
показать, что состояние | e > может быть
-
156 -
определено
для оператора (6) следующим образом. Пусть
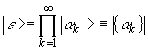 (7)
(7)
где
ak
| a
k
> = a k
| a
k
> (8)
Тогда
прямая подстановка (7) в (5) показывает, что последнее обращается
в тождество для собственного значения
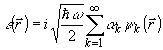 (9)
(9)
Полнота
системы функций | e > позволяет найти когерентное
представление для матрица плотности любого поля, заданного
на S. Мы, однако, ограничимся лишь так называемыми квазиклассическими
поляки, для которых р имеет диагональный вид:
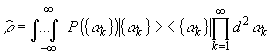 (10)
(10)
Нетрудно
убедиться, что Р({a k}) нормирована
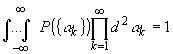 (11)
(11)
но,
в противоположность классической плотности вероятности,
не удовлетворяет условию неотрицательности. Вместе с тем,
для всех ансамблей, имеющих классические аналоги, Р ({a
k}) ³ 0, и в этом случае мы можем последовательно
интерпретировать
-
157 -
Р({a
k}) как совместную плотность вероятности множества
комплексных амплитуд осцилляторов {a k}.
В частности, если
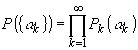 (12)
(12)
то
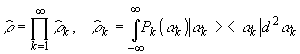 (13)
(13)
и
возбуждаемые моду статистически независимы. Как и для классической
системы такие типы колебаний определяют степени свободы
изображения. Задавая полный набор наблюдаемых {N(k)},
каждая из которых действует в пространстве волновых функций
соответствующего осциллятора, получим систему независимых
измерений в бесконечном множестве параллельных одномерных
каналов. В информационном смысле, однако, этот измерительный
процесс не полностью аналогичен соответствующей классической
модели. Действительно, рассмотрим среднее количество информации
Ik(D ,Q), содержащейся в измерений d
(k) о сигнале g(k) в k-том одномерном
канале (ниже для простоты индекс к будем опускать):
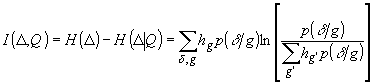 (14)
(14)
где
Н(D ) - энтропия измерения на выходе;
Н(D
| Q) - условная энтропия при фиксированном состоянии
на входе;
hg
- априорная вероятность "сигнала" g;
p(d
| g) - вероятность измерения d при фиксированном
g.
Особенности
квантовой теории проявляются как раз в определении
-
158 -
p(d
| g). В идеальной классической системе без щупов вход и выход связаны однозначно,
тогда как квантовомеханические измерения и в этом случае дают лишь статистическую
связь g и d . Используем модель процесса регистрации, согласно которой
приемное устройство, выполняя идеальное квантовое измерение N, дает оценку сигнала
g, соответствующую математическому ожиданию некоторого проекционного оператора
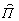 [g],
[g],
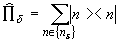 (15)
(15)
где | n
> - собственная функция N, соответствующая собственному значению n, а суммирование
распространено на область значений {nd }, каждая точка которой определяет
решение d . В дальнейшем для простоты полагается 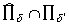 если d ¹ d ' и
если d ¹ d ' и 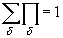 .
Для состояния полевого осциллятора, задаваемого матрицей плотности
.
Для состояния полевого осциллятора, задаваемого матрицей плотности 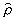 ,
найдем тогда
,
найдем тогда
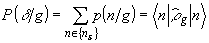 (16)
(16)
Вычисления
завершаются определением r g по заданному
состоянию не входе канала Для линейного квантовомеханического
фильтра можно положить /10/:
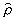 g
= Т(s g) (17)
g
= Т(s g) (17)
где Т -
оператор, действующий в пространстве матриц плотности, .на который наложен ряд
условий, вытекающих из положительной определенности и нормировки 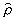 g.
Если
g.
Если 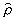 g и
g и 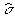 g
допускают диагональное представление по когерентным состояниям вида
g
допускают диагональное представление по когерентным состояниям вида
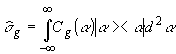 (18)
(18)
-
159 -
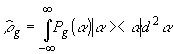 (19)
(19)
нетрудно
показать, что (17) эквивалентно интегральному преобразованию
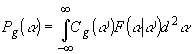 (20)
(20)
где
F(a | a ') - весовая функция, определяемая
прохождением сигнала через канал:
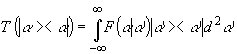 (21)
(21)
В
свою очередь, переходные вероятности р(n | g) выражаются
через F(a | a '):
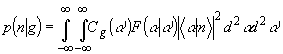 (22)
(22)
В
частности, если регистрирующий прибор есть идеальный квантовый
счетчик, то есть N - оператор числа фотонов, то
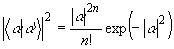 (23)
(23)
Для
определения F(a | a ') необходимо рассматривать
конкретную модель канала. Пусть, например, Т - тождественное
преобразование (измерение производится над входным сигналом
непосредственно). Тогда
T
º 1; F(a |
a
') = d (2)(a
- a ') (24)
-
160 -
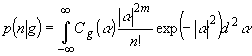 (25)
(25)
Определение
условных вероятностей р(n | g) для заданного способа
измерения я решающего правила (выбор областей {ns})
полностью характеризует информационную эффективность квантово-механического
канала, формирующего изображения. В частности, полная энтропия
выходного сигнала для измерений {N(k)}
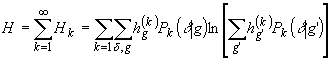 (26)
(26)
а
полное количество информации в изображении
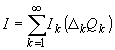 (27)
(27)
Величины
I и Н служат хорошими оценками качества изображающей систему
при заданном способе измерения. Было бы, конечно, желательно
максимизировать их, варьируя метод регистрации, однако,
обычно эта задача очень сложна и решается лишь для простейших
случаев. Рассматривая, например, бинарный одномерный канал
(черно-белое изображение), можно подучить оптимальные рещавдие
правила, сводящиеся к пороговым условиям для n(k).
В большинстве
случаев, однако, модовое разложение (6) не означает автоматически статистическую
независимость полевых осцилляторов (12), так что оптический канал не сводится
непосредственно к совокупности одномерных, и применение приведенных ваше соотношений
оказывается невозможным. Ввиду этого попутаемся найти такое преобразование операторов-амплитуд
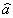 k, которое обеспечивало
он их взаимную некоррелированность. Другими словами, положим
k, которое обеспечивало
он их взаимную некоррелированность. Другими словами, положим
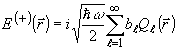 (28)
(28)
-
161 -
где операторы
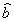 ℓ и
ℓ и 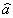 k
связаны преобразованием:
k
связаны преобразованием:
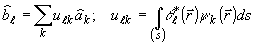 (29)
(29)
и
удовлетворяют соотношениям
<b+ℓbℓ’>
= Sp(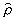 b+ℓbℓ’)
= l ℓd
ℓℓ’ (30)
b+ℓbℓ’)
= l ℓd
ℓℓ’ (30)
Из полноты
и ортонормированности систем базисных функций {q ℓ} и
{y k} следует унитарность преобразования (29), 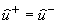 ',
так что оператору
',
так что оператору 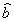 ℓ
сохраняют свойства операторов уничтожения фотонов в полевом осцилляторе ℓ,
пространственная модовая функция которого не является более нормальным решением
уравнения Гельмгольца для выбранных граничных условий. Однако, благодаря (30),
такие осцилляторы некоррелированы в первом порядке и неудобства перехода к сложным
пространственным функциям q ℓ(
ℓ
сохраняют свойства операторов уничтожения фотонов в полевом осцилляторе ℓ,
пространственная модовая функция которого не является более нормальным решением
уравнения Гельмгольца для выбранных граничных условий. Однако, благодаря (30),
такие осцилляторы некоррелированы в первом порядке и неудобства перехода к сложным
пространственным функциям q ℓ(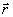 )
вполне компенсируются преимуществами при расчете информационных характеристик.
Используя, далее, соотношение
)
вполне компенсируются преимуществами при расчете информационных характеристик.
Используя, далее, соотношение
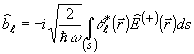 (31)
(31)
и полноту
системы {q ℓ(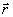 )},
найдем из (30) уравнение
)},
найдем из (30) уравнение
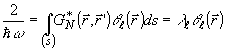 (32)
(32)
которое
отличается от соответствующего классического лишь несущественной
нормировкой собственных значений и заменой корреляционной
функции комплексных амплитуд нормально упорядоченной корреляционной
-
162 -
функцией.
Это второе отличие физически более интересно и требует специального анализа.
Здесь мы заметим лишь, что для квазиклассических полей GN(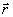 ,
,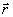 ’)
формально совпадает с обычным определением корреляционной функции, поскольку
’)
формально совпадает с обычным определением корреляционной функции, поскольку
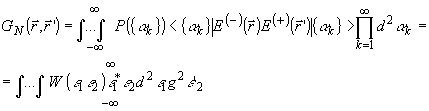 (33)
(33)
где e
i º e (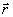 i);
i = 1,2, a W(e 1e 2) - двумерное распределение комплексной
амплитуды поля /7/:
i);
i = 1,2, a W(e 1e 2) - двумерное распределение комплексной
амплитуды поля /7/:
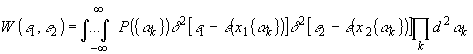 (34)
(34)
Как и в
классическом случае, ядро GN(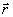 ,
,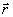 ’)
определяет самосопряженный неотрицательно-определенный оператор типа Гильберта-Шмидта,
так что все основные свойства решений (32), приведенные в /1/ сохраняются. Замечая,
что b+ℓbk=Nℓ - оператор
числа фотонов в ℓ-том полевом осцилляторе, видим, таким образом, что l
ℓ представляет собой среднюю заселенность соответствующей моды,
а полная энергия ноля
’)
определяет самосопряженный неотрицательно-определенный оператор типа Гильберта-Шмидта,
так что все основные свойства решений (32), приведенные в /1/ сохраняются. Замечая,
что b+ℓbk=Nℓ - оператор
числа фотонов в ℓ-том полевом осцилляторе, видим, таким образом, что l
ℓ представляет собой среднюю заселенность соответствующей моды,
а полная энергия ноля
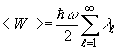 (35)
(35)
Пусть,
например, корреляционная функция поля представлена в виде
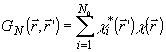 (36)
(36)
-
163 -
Тогда
интегральное уравнение (32) вырождено в имеет N0,
отличный от нуля собственных значений, а, следовательно,
в ансамбле изображений возбуждается конечное число мод.
Справедливо и обратное утверждение: если изображение имеет
конечное число степеней свободы, его корреляционная функция
представима в виде (36), поскольку в общем случае
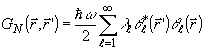 (37)
(37)
Заметим,
что рассмотренный ансамбль полностью эквивалентен исследованному
в /1/ для апертуры, состоящей из точечных элементов.
Не
представляет труда получить теперь и обычные информационные
опенки качества оптической изображающей системы с учетом
квантовых поправок. Так, например, число эффективных степеней
свободы в изображении определяется по относительному уровню
ошибки и l ℓ аналогично формуле (6)
из /1/. Используя (26) и (27), можем найти и более детальные
характеристики системы. В качестве примера определим энтропию
квантового ансамбля изображений на одномерной апертуре для
экспоненциально коррелированного Гауссового источника. Пусть
оценка принятого сигнала производится по измеренному значению
чисел заполнения в каждом одномерном канале, т.е. d
k º nk, Тогда (26) преобразуется
к виду
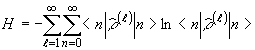 (38)
(38)
где
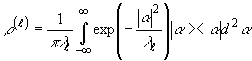 (39)
(39)
Непосредственное
вычисление (38) приводит к
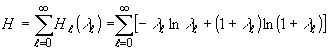 (40)
(40)
-
164 -
Находя
решение уравнения (32) для
GN(х,х’)
= I0ехр(-| x - x'| /x0) (41)
где
I0 - средняя интенсивность излучения, получим
/11/:
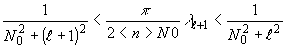 (42)
(42)
где
N0 = S/p x0 - число Шеннона для
апертуры S и ширины пространственных частот
W
= 1/x0; <n> = 2I0S/ħw
Учитывая,
что обычно N0 >> 1, аппроксимируем l
ℓ+1 правой частью неравенства (42) и заменим
суммирование в (40) соответствующим интегрированием. В результате
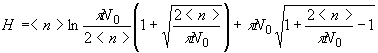 (43)
(43)
Из
(43) можно получить классическое <n>/N0
>> 1 и квантовое <n>/N0 <<
1 приближение для H. Можно показать, что квантовый пространственный
канал имеет ограниченную информационную эффективность даже
при отсутствии шума.
Таким
образом, изложенный метод позволяет провести полный квантово-механический
анализ линейной оптической системы, формирующей изображение.
-
165 -
Литература
1.
В.Н.Курашов. Материалы Х Всесоюзной школы по голографии,
Л., 1978.
2.
Б.А.Гришанин. Материалы VII Всесоюзной школы по голография,
Л.., стр.118, 1975.
3.
С, Helstrom, :Progress in Optics”, ed. E.Wolf, v. 10, North-Holland
Pub. Company, Amsterdam - London, p. 290, 1972.
4.
В.Н.Курашов. Материалы VIII Всесоюзной школы по голографии,
Л., стр.130, 1976.
5.
И.А.Дерюгин, В.Н.Курашов. "Проблемы голографии", межвузовский
сборник научных трудов, вып.4, М., стр.41, 1974.
6.
В.В.Митюгов. Физические основы теории информации, "Сов.
Радио", М., 1976.
7.
Р.Глаубер. Оптическая когерентность и статистика фотонов,
в кн. "Квантовая оптика и квантовая радиофизика", "Мир",
М., стр.88, 1966.
8.
Дж.Клаудер, Э.Сударшан. Основы квантовой оптики, "Мир",
М., 1970.
9.
R.X.Stratonovich, J. Of Statistics, 1, 67 (1973),
10.
В.Л.Белавкин. Доклады VII Всесоюзной конференции по теории
кодирования и передачи информации, ч.1. Москва-Вильнюс,
стр.23, 1978.
11.
J. Chalr, Proc, JEE, pt III, 97, 88 (1950).

