|
|
 |
 |

|
| |
ДИНАМИЧЕСКИЕ ГОЛОГРАММЫ НА СУПЕРПОЗИЦИОННЫХ СОСТОЯНИЯХ АТОМОВ
Е.И.Штырков
Рассматривается возможность формирования динамических голограмм в резонансной среде на когерентных суперпозиционных состояниях атомов. Обсуждаются особенности записи и восстановления волновых фронтов света на таких голограммах при возбуждении среды импульсными объектным и опорным поляки, подаваемыми на среду неодновременно.
I. ИНТЕРФЕРЕНЦИЯ АТОМНЫХ СОСТОЯНИЙ
Метод динамической голографии, как известно /1-7/, основан на взаимодействии когерентного излучения с веществами, характеристики которых могут обратным образом изменяться под действием световых волн и, в свою очередь, влиять на эти волны. Особенно интересно использовать в качестве регистрирующей среды вещества, которые имеют энергетические переходы, резонансные частоте воздействующего поля. В условиях резонанса все взаимодействия происходят более эффективно, и многие нелинейные и параметрические явления могут наблюдаться при довольно умеренных напряженностях воздействующих полей. Чтобы записать динамическую голограмму в резонансной среде, необходимо подать на нее одновременно объектную и опорную волны с частотой, близкой частоте энергетического перехода. При этом в пучностях интерференционной картины активные центры перейдут в верхнее энергетическое состояние и информация о волновом фронте объектной волны будет сохраняться в течение эффективного времени жизни этого состояния (в случае пренебрежения диффузией возбужденных частиц). Эта информация может быть восстановлена как путем пропускания через голограмму плоской считывающей волны /1,2/, так и при самодифракции
- 119 –
опорной волны /2-5/. Рассмотрим, однако, более интересный случай, когда используются когерентные свойства самой атомной системы. Известно, что после начала когерентного возбуждения атомной системы прежде, чем атомы окажутся в одном из основных состояний, имеет место переходный процесс. В это время система атомов переходит в состояние, являющееся когерентной суперпозицией начального (нижний уровень) и конечного (верхний уровень) состояний. В этом случае частицы проводят лишь часть времени в каждом из этих состояний и динамика сложного движения их такова, что система приобретает неравновесную когерентную электрическую поляризацию. Когерентность системы сохраняется в течение времени релаксации неравновесной поляризации среды (время фазовой памяти системы). В это время система атомов находится в когерентном суперпозиционном состоянии:
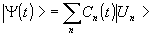 (1) (1)
где | Un > - векторы собственных состоянии с энергиями Wn, Cn(t)=Cnexp[-iWnt/L] - полученные из решения уравнения Шредингера комплексные коэффициенты, представляющие собой гармонические колебания с фазой, частотой и амплитудой. Эти колебания определяют характер поведения во время различных свойств возбужденной атомной системы. Рассмотрим, например, математическое ожидание какой-либо интересующей нас физической величины, определяемой неким оператором 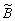 . .
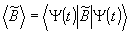 (2) (2)
что после использования /1/ приводит к
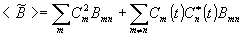 (3) (3)
Здесь Bmn = <Un|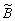 |Um> - матричные элементы оператора |Um> - матричные элементы оператора 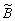 . Среднее значение физической величины < . Среднее значение физической величины <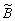 >, измеряемое на опыте, может быть получено после усреднения /3/ по статистическому >, измеряемое на опыте, может быть получено после усреднения /3/ по статистическому
- 120 -
ансамблю из независимых атомов, т.е. путем операции
<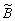 > = Sp( > = Sp(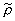 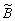 ) (4) ) (4)
где 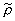 - матрица плотности для ансамбля атомов, элементы которой равны: - матрица плотности для ансамбля атомов, элементы которой равны:
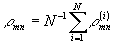 ; ; 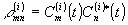
Итак, если система атомов приготовлена когерентным образом, т.е. недиагональные элементы матрицы плотности r
mn отличны от нуля (фактор когерентности gmn = r
mn(t)/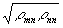 нe равен нулю /8/, то второй, член в /3/ не исчезает после усреднения /4/ и его величина зависит от соотношения фаз и амплитуд вероятностей Сm нe равен нулю /8/, то второй, член в /3/ не исчезает после усреднения /4/ и его величина зависит от соотношения фаз и амплитуд вероятностей Сm(t), Сn(t). Этот член является выражением интерференции атомных состояний, в значительной мере может влиять на величину изучаемой характеристики атомной системы и существует в течение времени фазовой памяти системы, т.е. времени когерентности между основными состояниями |
Un> и |Um>. В это время в системе атомов могут иметь место различные переходные квантовые эффекты, такие как пересечения атомных уровней, квантовые биения /9,10/, фотон-эхо /11,12/, самоиндуцированная прозрачность /13/ и другие явления /14/. Все эти явления могут быть положены в основу для записи динамических голограмм в резонансной среде в условиях переходного процесса. Этот вывод следует из универсальности голографического подхода, основанного на интерференции когерентных волн независимо от их природы. Следствием этого является то обстоятельство, что возбуждающие атомную систему импульсные объектное и опорное поля могут воздействовать на среду неодновременно. Тем не менее, информация о волновых фронтах этих полей будет сохраняться системой в течение переходного процесса и голограмма будет формироваться в результате интерференции атомных состояний /15/. Продемонстрируем это на конкретном примере, определив пространственное распределение коэффициента поглощения среды после воздействия на нее объектным и опорным импульсными полями.
- 121 -
II. УРАВНЕНИЕ ГОЛОГРАММЫ
Допустим, что используемая среда представляет собой двухуровневую невырожденную систему атомов, условия возбуждения которой представлены на рис.1 .
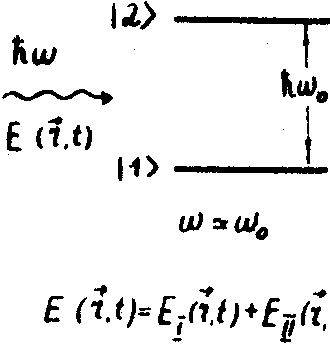 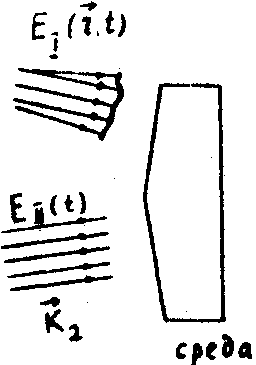 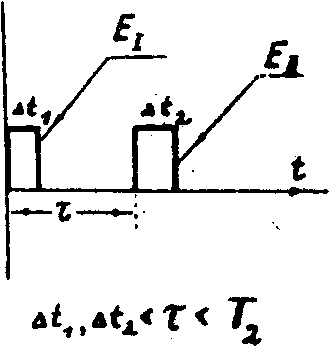
Рис.1. Пространственно-временные условия резонансного возбуждения атомной системы, а)по частоте , б)по пространству, в) по времени. (Т2 - время релаксации неравновесной поляризации).
Для простоты объектную (Е I) и опорную (ЕII) волны выберем, соответственно, в виде квазиплоскости (фазовое возмущение волнового фронта j
1( 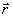 ) - мало, где 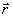 - радиус вектор) и плоской линейнополяризованной волн: - радиус вектор) и плоской линейнополяризованной волн:
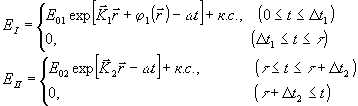
Здесь 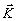 1, 1, 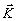 2 - волновые векторы, а к.с. - комплексносопряженное 2 - волновые векторы, а к.с. - комплексносопряженное
- 122 -
выражение. Теперь характеристики среды, возбужденной таким образом, можно найти из /4/, предварительно определив соответствующий оператор интересующего нас параметра и решив квантовомеханическое уравнение движения для матрицы плотности системы (см., например /8/). Однако, можно пойти более простым путем, если выразить интересующие нас характеристики через компоненты средних значений оператора энергетического спина 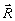 = 1/2 /16,17/ и найти эти компоненты из решений дифференциальных уравнений типа уравнений Блоха, взятых, например, из работы /12/, = 1/2 /16,17/ и найти эти компоненты из решений дифференциальных уравнений типа уравнений Блоха, взятых, например, из работы /12/,
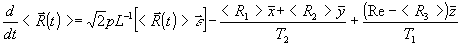 (6) (6)
Здесь р - модуль дипольного момента перехода <21 «
1; ħ = 1,05·10-34 дж.с.; 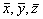 - орты по осям координат; <R1>, <R2> - средние значения поперечных компонент энергетического спина (предполагается, что свет направлен по оси OZ; <R3> - продольная компонента, равновесное значение которой Re; T2, T1 - соответственно, времена поперечной и продольной релаксации. Вектор, - орты по осям координат; <R1>, <R2> - средние значения поперечных компонент энергетического спина (предполагается, что свет направлен по оси OZ; <R3> - продольная компонента, равновесное значение которой Re; T2, T1 - соответственно, времена поперечной и продольной релаксации. Вектор, 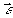 связан с возбуждающей циркулярнополяризованной волной в виде /12/ связан с возбуждающей циркулярнополяризованной волной в виде /12/
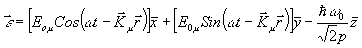
m
- индекс импульса.
Характерно , что поперечные и продольные компонента энергетического спина релаксируют с разными скоростями. Время поперечной релаксации Т2 характеризует потерю когерентности в системе (это время выше было определено как время релаксации неравновесной поляризации среда), a Т1 - связано с энергетическим балансом и определяет стремление системы к термодинамическому равновесию. В большинстве случаев время поперечной релаксации меньше времени продольной релаксации и в зависимости от условий может принимать значения 10-6 ¸
10-12 с. Компоненты энергетического спина определяют как поляризацию среды Р, так и разность населенности D
N(t) для нижнего (N1) и верхнего (N2) уровней в виде (см., например, /8|)
- 123 -
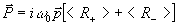 (7) (7)
D
N(t) = N1 – N2 = 2<R3> (8)
где <R±
> = <R1> ± i<R2>, N1 + N2 = N0 - концентрация активных центров. Населенность уровней и поляризаций среды при любой последовательности возбуждения ее импульсными полями можно найти из /7/ и /8/, если воспользоваться значениями <R±
> и <R3>, полученными в работе /18/ из решения уравнения /6/ методом преобразования Лапласа при переходе во вращающуюся систему координат. Эти решения для случая D
t << t
< Т2, Т (приближение коротких импульсов), w
»
w
0 (точный резонанс), а также E0m
>> ħ/pT2 (случай сильного поля) имеют довольно простой вид:
а)во время действия импульса с амплитудой поля
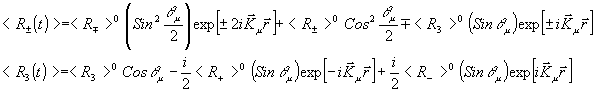 (9) (9)
б) при снятии возбуждения
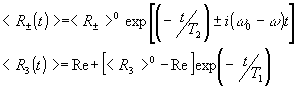 (10) (10)
- 124 -
Здесь q
m
= 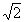 pħ-1E0m
D
t0m
- так называемая импульсная площадь, которая имеет размерность угла. Физически q
m
характеризует угол поворота диполъного момента под действием приложенного поля. В этих выражениях индекс "о" обозначает начальные значения величин. Используя /9/ и /10/, поэтапно можно рассчитать все компоненты при любой комбинации возбуждающих прямоугольных импульсов. Необходимо только при переходе к следующему временному этапу в качестве начальных условий брать конечные решения предыдущего этапа. До начала возбуждения система находится в состоянии термодинамического равновесия и только продольная компонента энергетического спина отлична от нуля, т.е. для t = 0 имеет место <R±
>0 = 0, <R3>0 = Re (для оптических переходов можно считать, что при равновесии верхний уровень не заселен, т.е. D
N = 2Re = N0. В нашем конкретном примере (рис.1) необходимо поля EI и EII разложить на циркулярно поляризованные компоненты и поэтапно использовать /9/ и /10/. Тогда с учетом /8/ путем простых, но довольно громоздких выкладок можно получать для разности населенностей в момент времени после воздействия вторым импульсом (t > t
+ D
t2) выражение вида pħ-1E0m
D
t0m
- так называемая импульсная площадь, которая имеет размерность угла. Физически q
m
характеризует угол поворота диполъного момента под действием приложенного поля. В этих выражениях индекс "о" обозначает начальные значения величин. Используя /9/ и /10/, поэтапно можно рассчитать все компоненты при любой комбинации возбуждающих прямоугольных импульсов. Необходимо только при переходе к следующему временному этапу в качестве начальных условий брать конечные решения предыдущего этапа. До начала возбуждения система находится в состоянии термодинамического равновесия и только продольная компонента энергетического спина отлична от нуля, т.е. для t = 0 имеет место <R±
>0 = 0, <R3>0 = Re (для оптических переходов можно считать, что при равновесии верхний уровень не заселен, т.е. D
N = 2Re = N0. В нашем конкретном примере (рис.1) необходимо поля EI и EII разложить на циркулярно поляризованные компоненты и поэтапно использовать /9/ и /10/. Тогда с учетом /8/ путем простых, но довольно громоздких выкладок можно получать для разности населенностей в момент времени после воздействия вторым импульсом (t > t
+ D
t2) выражение вида
D
N(t) = N0[1 + (A – 1)exp{-(t - t
)/T1} (11)
где A = Cosq
1Cosq
2 - (Sinq
1Sinq
2)exp[-t
/T2]СоsФ(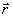 ), Ф( ), Ф(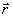 ) = D ) = D
 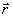 + j
1( + j
1(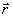 ) + w
0t
, D ) + w
0t
, D
 =( =( 1 - 1 -  2) -вектор решетки. Из этого выражения прежде всего следует, что в резонансной среде при возбуждении ее двумя импульсными полями, которые не могут интерферировать друг с другом непосредственно (D
t << t
), тем не менее, формируется локализованная в пространстве решетка (интерферограмма) с шагом L
=2p
/|
D 2) -вектор решетки. Из этого выражения прежде всего следует, что в резонансной среде при возбуждении ее двумя импульсными полями, которые не могут интерферировать друг с другом непосредственно (D
t << t
), тем не менее, формируется локализованная в пространстве решетка (интерферограмма) с шагом L
=2p
/|
D
 |
. Эта интерферограмма содержит фазовую информацию об объектной волне и имеет обычный для такого случая (слабовозмущенного волнового фронта) вид голограммы. Эта голограмма распадается со временем продольной релаксации. Влияние поперечной релаксации сказывается на глубине пространственной модуляции формируемой решетки. Естественно, чем быстрее будет подана опорная волна (t
<< T2) после воздействия объектного поля, тем меньше будет потеря когерентности у системы к моменту подачи этой |
. Эта интерферограмма содержит фазовую информацию об объектной волне и имеет обычный для такого случая (слабовозмущенного волнового фронта) вид голограммы. Эта голограмма распадается со временем продольной релаксации. Влияние поперечной релаксации сказывается на глубине пространственной модуляции формируемой решетки. Естественно, чем быстрее будет подана опорная волна (t
<< T2) после воздействия объектного поля, тем меньше будет потеря когерентности у системы к моменту подачи этой
- 125 -
волны, а значит, больше глубина модуляции решетки (exp[-t
/T2] »
1). Кроме того, глубина пространственной модуляции голограммы периодическим образом зависит от импульсной площади возбуждающих полей. В зависимости от степени возбуждения D
N может принимать либо положительное (N1 > N2 - поглощение), либо отрицательное значения (N1 < N2 - усиление). Для простоты положим, что характеристики обоих импульсов одинаковы (E01 = Е02 = E 0, D
t 1 = D
t 2 = D
t, q
1 = q
2 = q
, j
1( 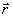 ) = 0). Тогда непосредственно после подачи второго импульса (t - t
<< Т1) коэффициент поглощения на частоте w
0 будет иметь вид:
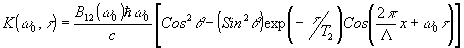 (12) (12)
где В 12( w
0)- спектральный коэффициент Эйнштейна, С - скорость света, вектор решетки направлен по оси ОХ. На рис. 2 приведены примеры влияния параметров возбуждения на характер коэффициента поглощения решетки.
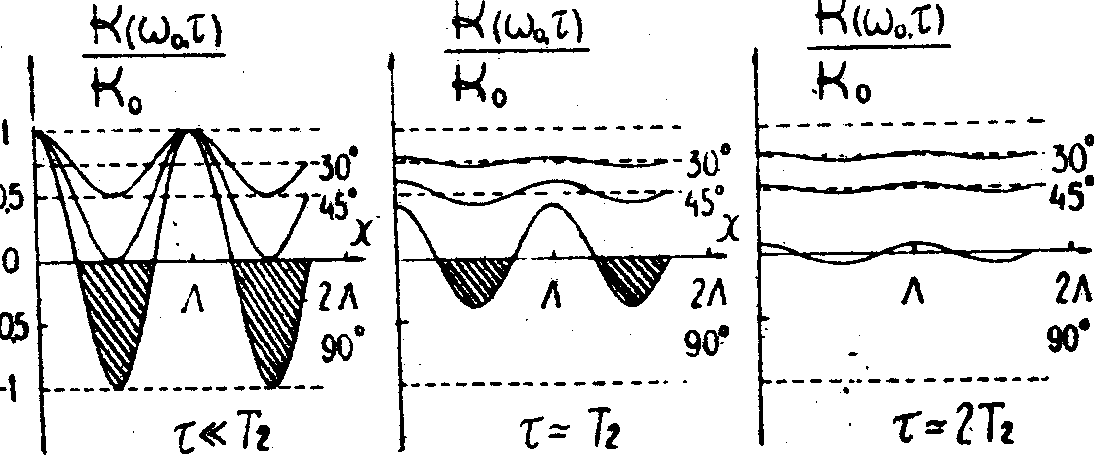
Рис.2. Коэффициент поглощения светоиндуцированных решеток.
При увеличении импульсной площади до 45° Глубина модуляции решетки достигает 100%. При этом коэффициент поглощения положителен. При q
> 45° в решетке появляются инверсные области (заштриховано на рис.2) с отрицательным поглощением. Как видно из выражения /12/, контраст инверсной решетки максимален при q
= mp
/2 (m = 1, 2, 3 ...). До сих пор мы полагали, что частицы не имеют разброса
- 126 -
по резонансным частотам w
0, т.е. рассматривали поведение лишь одной изохроматы из спектра частот. Однако, в реальных системах практически всегда имеет место такой разброс из-за неоднородного уширения перехода (d
w
0 ¹
0 ). Поэтому, при большом разбросе d
w
0 набег фазы w
0t
в выражении /12/ может привести к различным смещениям решеток, соответствующих разным иэохроматам, и к полному пространственному размытий локализованной решетки. Если смещение полос интерферограммы не превышает L
/10, то, как это обычно принимают, решетку можно считать локализованной. В нашем случае это приводит к условию
d
w
0t
> p
/S (13)
Обычно даже в случае сильного неоднородного уширения перехода монохроматическая волна аффективно взаимодействует лишь с изохроматами, расположенными вблизи частоты возбуждения в пределах, примерно d
w
0 = 2(Т2) -1, что обусловливает выжигание провалов /19/ на кривой неоднородного уширения перехода. С учетом этого условия /13/ может быть записано в виде
t
/T2 < 0,3 (14)
Это условие может быть использовано в качестве критерия для получения практически четкой интерферограммы.
III . ВОССТАНОВЛЕНИЕ ВОЛНОВЫХ ФРОНТОВ СВЕТА
После возбуждения через время, соизмеримое с Т 2, система атомов из когерентного суперпозиционного состояния переходит в смешанное. Несмотря на то, что когерентность системы разрушается. характер пространственного распределения возбужденных атомов /11/ сохраняется до окончания перехода системы в термодинамическое равновесие. Поэтому информацию об объектной волне ЕI /5/ можно восстановить обычным образом, подав слабую плоскую считывающую волну с частотой w
0 и волновым вектором  3 в любой момент времени t
< t < Т1 3 в любой момент времени t
< t < Т1. Тогда при дифракции этой волны в направлении ( 3 + D 3 + D
 ), как обычно, распространяется прямая, волна (волновой фронт совпадает с фронтом объектной волны EI), а в направлении ( ), как обычно, распространяется прямая, волна (волновой фронт совпадает с фронтом объектной волны EI), а в направлении ( 3 - D 3 - D
 ) )
- 127 -
распространяется обращенная волна (комплексносопряженный волновой фронт).
Однако, нас интересуют когерентные свойства самой системы атомов на стадии переходного процесса (t
< Т2). Поэтому, целесообразно подробнее остановиться на этой стадии, когда информация об объектной волне может выявляться в процессе самовоздействия волн, например, при самодифракции опорной волны. Как и в обычном случае, записи динамических голограмм, когда волны, формирующие решетку, сами на ней не дифрагируют /3/, в данном случае опорная волна при прохождении через среду с пространственно-модулированным поглощением /12/ должна испытывать самодифракцию. Во время воздействия второго импульса параметр q
2 изменяется линейно во времени, глубина пространственной модуляции голограммы /11/ также изменяется, и это вызывает изменение условий самодифракции опорного пучка. Качественную картину можно изучить, если искать результирующее поле когерентного отклика системы в этот момент времени в волновой зоне (на расстоянии R0 >> l
) в дипольном приближении
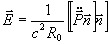 (15) (15)
где 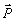 - поляризация среды, - поляризация среды, 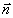 - единичный вектор в направлении наблюдения. Поскольку поляризация среды определяется поведением поперечных компонент энергетического спина /7/, для поля, излучаемого системой, можно записать (см./7/): - единичный вектор в направлении наблюдения. Поскольку поляризация среды определяется поведением поперечных компонент энергетического спина /7/, для поля, излучаемого системой, можно записать (см./7/):
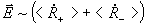 (16) (16)
Поэтапное использование выражений /9/ и /10/, а также для интервала времени t
<t<r+D
t2 приводит к
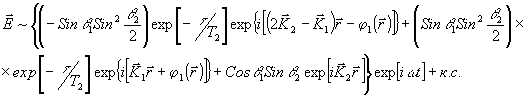 (17) (17)
- 128 -
Как видно из этою выражения, во время прохождения опорной волны через среду, она разбивается на три компоненты: прямую волну (волновой вектор  1), обращенную волну (вектор 2 1), обращенную волну (вектор 2 2 - 2 -  1) и плоскую волну (вектор 1) и плоскую волну (вектор  2). Рассмотрим случай, когда импульсная площадь первого импульса равна 90°. При таком режиме накачки Cosq
1 = 0 и последний член в /17/ обращается в нуль независимо от параметров второго импульса. Поскольку во время второго импульса q
2 линейно изменяется, то, как следует из /17/, происходит периодическая во времени перекачка энергии из прямой волны в обращенную и обратно. Например, при q
2 = p
/2 эти волны имеют одинаковую интенсивность. Решетка в это время инверсна и имеет максимальную глубину (см. рис.2). При дальнейшем увеличении q
2 интенсивность обращенной волны растет, а интенсивность прямой падает и при q
2 2). Рассмотрим случай, когда импульсная площадь первого импульса равна 90°. При таком режиме накачки Cosq
1 = 0 и последний член в /17/ обращается в нуль независимо от параметров второго импульса. Поскольку во время второго импульса q
2 линейно изменяется, то, как следует из /17/, происходит периодическая во времени перекачка энергии из прямой волны в обращенную и обратно. Например, при q
2 = p
/2 эти волны имеют одинаковую интенсивность. Решетка в это время инверсна и имеет максимальную глубину (см. рис.2). При дальнейшем увеличении q
2 интенсивность обращенной волны растет, а интенсивность прямой падает и при q
2 = p
система излучает только обращенную волну в направлении (2 2 - 2 -  1). Как следует из /11/, решетка в это время исчезает. Дальнейшее увеличение q
2 снова приводит к формированию решетки и появлению приямой волны ( 1). Как следует из /11/, решетка в это время исчезает. Дальнейшее увеличение q
2 снова приводит к формированию решетки и появлению приямой волны ( 1). Однако, необходимо заметить, что при этом инверсные и поглощающие области решетки поменялись местами, т.е. решетка скачком сдвигается на половину своего шага (L
/2). Таким образом, динамика взаимодействия света со средой такова, что процесс периодически повторяется. Рассмотрим еще одно интересное явление, наблюдаемое на стадии переходного процесса, которое может быть использовано для восстановления волновых фронтов. Известно, что при пропускании через неоднородно уширенную резонансную систему атомов двух оптических импульсов, разделенных интервалом t
< Т2, эта система излучает когерентный отклик в направлении (2 1). Однако, необходимо заметить, что при этом инверсные и поглощающие области решетки поменялись местами, т.е. решетка скачком сдвигается на половину своего шага (L
/2). Таким образом, динамика взаимодействия света со средой такова, что процесс периодически повторяется. Рассмотрим еще одно интересное явление, наблюдаемое на стадии переходного процесса, которое может быть использовано для восстановления волновых фронтов. Известно, что при пропускании через неоднородно уширенную резонансную систему атомов двух оптических импульсов, разделенных интервалом t
< Т2, эта система излучает когерентный отклик в направлении (2 2 - 2 -  1) в момент времени 2r /11,12/. Это так называемое первичное фотон-эхо. В работе /21/ было показано, что, если импульс света имеет сложный волновой фронт (объектная волна), а второй импульс - плоская волна, то первичное фотон-эхо является обращенной волной, т.е. содержит псевдоскопическое изображение объекта. Условие фазового синхронизма 1) в момент времени 2r /11,12/. Это так называемое первичное фотон-эхо. В работе /21/ было показано, что, если импульс света имеет сложный волновой фронт (объектная волна), а второй импульс - плоская волна, то первичное фотон-эхо является обращенной волной, т.е. содержит псевдоскопическое изображение объекта. Условие фазового синхронизма  эхо = 2 эхо = 2 2 - 2 -  1 и w
эхо »
w
не позволяет получать сигналы первичного эха при больших углах между опорной и объектной волнами. Поэтому при произвольной форме фронта объектной волны компоненты ее пространственного Фурье- спектра, которые составляют большой угол с опорным пучком, могут не восстанавливаться. Это может привести к искажению информации в отклике системы. Такое 1 и w
эхо »
w
не позволяет получать сигналы первичного эха при больших углах между опорной и объектной волнами. Поэтому при произвольной форме фронта объектной волны компоненты ее пространственного Фурье- спектра, которые составляют большой угол с опорным пучком, могут не восстанавливаться. Это может привести к искажению информации в отклике системы. Такое
- 129 -
ограничение по углу может быть снято для случая стимулированного фотон-эха. Стимулированное эхо - это когерентный отклик этой же системы, который возникает при подаче третьего импульса ( 3) света в момент времени t
< t < T2. Импульс эха формируется через время t
после третьего импульса в направлении 3) света в момент времени t
< t < T2. Импульс эха формируется через время t
после третьего импульса в направлении
 3- 3- 1+ 1+ 2. 2.
В работе /22/ показано, что, если опорная волна подается раньше объектной, а третий импульс является плоской волной, то волновой фронт стимулированного эха совпадает с волновым фронтом объектной волны. Условие фазового синхронизма для h
- компоненты пространственного Фурье - спектра стимулированного эха имеет вид:  эh
= эh
=  2h
+ 2h
+  3 - 3 -  1, w
эхо @
w
. Отсюда видно, при подаче считывающего луча в направлении опорного пучка ( 1, w
эхо @
w
. Отсюда видно, при подаче считывающего луча в направлении опорного пучка ( 3 = 3 =  1) условие синхронизма точно выполняется ( 1) условие синхронизма точно выполняется ( эh
= эh
=  2h
; w
эхо = w
). Это означает, что волновой фронт любой произвольной формы может быть восстановлен в отклике стимулированного эха без искажений. 2h
; w
эхо = w
). Это означает, что волновой фронт любой произвольной формы может быть восстановлен в отклике стимулированного эха без искажений.
Таким образом, когерентные суперпозиционные состояния атомных систем могут быть использованы для записи динамических голографических решеток. Исследование вопросов взаимодействия света с эти -ми решетками позволит расширить круг наших представлений, не только с точки зрения формирования, преобразования и восстановления волновых полей, но и при изучении фундаментальных аспектов когерентного взаимодействия света с веществом, исследования различных характеристик атомных систем и т.п.
Литература
1 .H.Gerritsen. J.Appl.Phys.Let., 10, 239, 1967, 14, 5, 159, 1969.
2. H.Eichler, B.Kluzovski. Z. Angew.Phys., 27, 4, 1969; 28, 306, 1970.
3. Е.Штырков. Письма в ЖЭТФ, 12, 3, 134, 1970.
4. J.Woerdman. Opt. Comm., 2, 1212, 1970.
5. В.Комиссаров. Письма в ЖЭТФ, 14, 64, 1971.
6. Б.Степанов, Е.Ивакин, А.Рубанов. ДАН СССР, 196, 3, 567, 1971.
7. А.Борщ, М.Бродин, В.Овчар, С.Одулов, М.Соскин. Письма в ЖЭТФ, 18, 11, 679, 1973.
8. В.Файн. Фотоны и нелинейные среды, 1, М., 1972.
9. Е.Александров. УФН, 107, 4, 595, 1972.
- 130 -
10. В.Показаньев, Г.Скроцкий. УФН, 107, 4, 623, 1972.
11. У.Копвиллем, В.Нагибаров. Физика металлов и металловедение, 15, 313, 1963.
12. I.Abella, K.Kurnit, S.Hartmann. Phys. Rev., 141, 1, 391, 1966.
13. S.McCall, E.Hahn. Phys.Rev.Lett., 18, 908, 1967.
14. H.Walther. Laser spectroscopy of atoms and molecules (Topics in Appl.Phys. v2, 1976), 2, 1-124, 1976. Springer-Verlag Berlin Heidelberg New York, 1976.
15. Е.Штырков. Оптика я спектроскопия, 1978.
16. R.Dicke. Phya. Rev., 93, 99, 1954.
17. R.Feinman, F.Vernon, R.Hellworth. J.Appl.Phys., 28, 49, 1957.
18. В.Самарцев, А.Шагидуллин. В кн. Электромагнитное сверхизлучение, 10-62, Казань, 1975.
19. W.Lanib. Phya.Rev., 134A, 1429, 1964.
20. Л.Ландау, Е.Лифшиц. Теория поля, ОГИЗ, 1946.
21. Е.Штырков, В.Самардев. В кн. Электромагнитное сверхизлучение, 398-426, Казань, 1975; Опт. и спектроскопия, 40, 392, 1976.
22. В.Самарцев, Е.Штырков. ФТТ, 19, 3140, 1976.
E.Shtyrkov, V.Samartsev. Phys.Stat.Sol. (a), 45, 1978.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

