|
|
 |
 |

|
| |
ОПТИЧЕСКИЕ ВОЛОКОННЫЕ ЛИНИИ ПЕРЕДАЧИ ИНФОРМАЦИИ
М.П.Петров, Е.А.Кузин
Рассматриваются физические основы работы оптического волокла. Кратко обсуждаются характерные особенности распространения света по оптическому волокну. Рассматриваются причины уширения и ослабления светового импульса при прохождении по оптическому волокну. Приведены основные результаты, достигнутые в технологии изготовления оптического волокна. Рассматривается возможность использования оптического волокна в качестве дисперсионной линии задержки для сжатия Ч.М. оптических импульсов.
Большое внимание, которое привлекает создание волоконно-оптических линий связи (ВОЛС), обусловлено рядом преимуществ волоконных линий по сравнению о кабельными. Прежде всего, это большая полоса пропускания (порядка 4 Ггц/км для волокон типа сельфок и в перспективе более 10 Ггц/км для одномодовых волокон) малое затухание сигнала (~ 10 дб/км - в пропыленном варианте и 0,5¸
1дб/км - для экспериментальных образцов), высокая помехозащищённость (поскольку электрические сигналы не создают помех в волокне), отсутствие излучения из волокна, малые веса волоконных кабелей, потенциально низкая стоимость. Все это обеспечивает большие практические возможности BOЛС в технике.
Одно из важнейших применений они находят в системах телефонной связи, где ВОЛС имеет несомненно лучшие параметры. Например, с помощью кабеля L - 1 фирмы Bell можно передать 1800 телефонных каналов на расстояние до 12,8 км, с помощью кабеля L -5 можно передавать 90000 каналов, но на расстояние всего 1,6 км. В то же время по ВОЛС можно передавать несколько сотен тысяч телефонных каналов на расстояние 15 ¸
40 км.
Принципиальная схема ВОЛС состоит из трех основных элементов (рис.1): источник света, оптического волокна и приемника света.
- 90 -

Рис.1. Принципиальная схема волоконно-оптической линии связи.
В качестве источника на схеме показан светодиод. Мощность его излучения пропорциональна протекающему току. При прохождении по светодиоду серии импульсов тока он вырабатывает точно такую же серию световых импульсов. Эти импульсы распространяются по волокну и попадают на фотодиод, который, в свою очередь, опять превращает выходное световые импульсы в электрические. Выходные электрические импульсы обрабатываются обычными радиотехническими методами.
Мы рассмотрим вопросы, касающиеся распространения света по оптическому волокну. В силу ограниченности места затронуты будут только самые основные проблема. Для более подробного изучения можно рекомендовать ряд обзоров и монографий, появившихся в последнее время /1 – 4/ .
- 91 -
В простейшем случае оптическое волокно представляет собой двухслойный стержень, состоящий из жилы с коэффициентом преломления n1, и оболочки с коэффициентом n2. При n1 > n2 свет, распространяющийся по сердцевине, может претерпевать полное внутреннее отражение на границе сердцевина-оболочка, если угол падения луча j
больше критического,
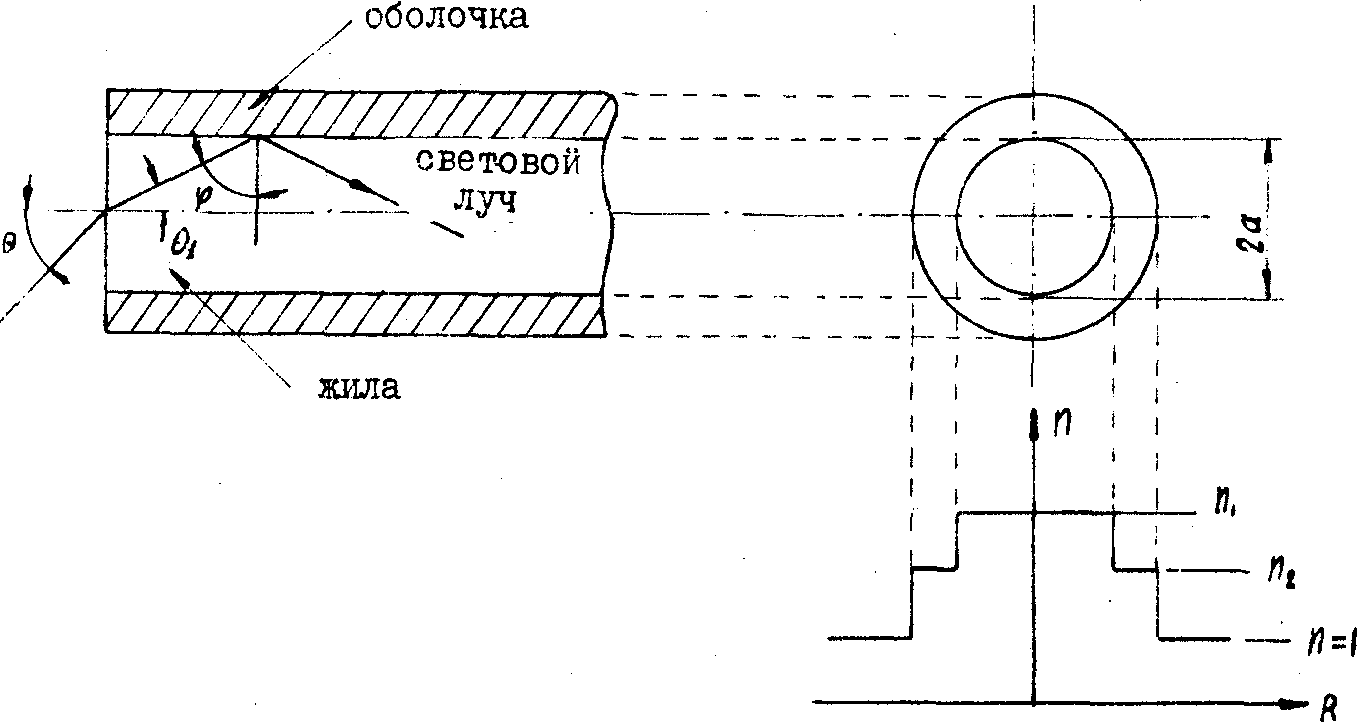
Рис.2. Распространение света по волокну со ступенчатым профилем коэффициента преломления.
Критический угол определяется формулой:
Sinj
min = n2/n1 (1)
В традиционном смысле определяется апертура оптического волокна
A = Sinq
max = 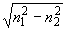 (2) (2)
Простейшие геометрические рассуждения показывают, что длина пути луча в волокне зависит от угла падения луча и определяется формулой:
P(q
1) = L/Cosq
(3)
- 92 -
где Р(q
1) - длина пути луча, L - длина оптического волокна.
Кроме рассмотренных меридиональных лучей, то есть лучей, которые проходят через ось волокна, могут существовать также косые лучи, не пересекающие ось волокна и распространяющиеся в волокне по ломаным винтовым линиям. Наличии косых лучей приводит к некоторому увеличению апертуры оптического волокна.
Геометрическая оптика достаточно хорошо описывает распространение света по волокну , если диаметр жилы значительно больше длины волны света. Когда диаметр жилы становится соразмерным с длиной волны, тогда необходимо переходить к волновому описанию распространения света по оптическому волокну.
Решение волновод задачи подробно изложено в известной книге Маркузе /2/. Мы ограничимся здесь обсуждением основных результатов. При решении задачи считают, что радиус оболочки равен бесконечности. Решение должно удовлетворять двум условиям. Во-первых, оно не должно расходиться в центре волокна, при R = 0 и, во-вторых, должно быстро убывать вне жилы при R ®
¥
. Второе условие означает, что мы рассматриваем только такие решения, которые описывают поля, сосредоточенные в жиле и примыкающих к ней областях.
Свет в оптическом волноводе распространяется в виде конечной суммы волноводных код. Каждая мода характеризуется распределением световой энергии и распространяется по волноводу со своей фазовой скоростью. Выберем цилиндрическую систему координат R,q
,Z так, чтобы ось волокна совпадала с Z. Зависимость от времени и от Z дается выражением ехр{i(b
z-w
t)}, где w
- круговая частота, b
- постоянная распространения.
Благодаря цилиндрической симметрии все компоненты поля могут быть выражены как функции Е Z и НZ, которые удовлетворяют волновому уравнению в цилиндрических координатах и для жилы имеют вид:
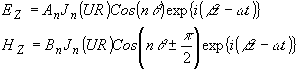 (4) (4)
- 93 -
Выражение для поля в оболочке получают путем замены постоянных An и Вn на Сn и Dn, а функции Бесселея Jn(UR). Ha модифицированную функцию Ханкеля первого рода Кn(WR). Поле оболочки может быть описано только этой функцией, так как она является единственной цилиндрической функцией, которая быстро стремится к нулю по мере увеличения R.
U и W определяются следующим образом:
U2 = K21 - b
2; W2 = b
2 - K22 (5)
где К 1 - волновое число света в жиле, К2 - волновое число в оболочке .
Поперечные компоненты поля могут быть выражены как функции EZ и НZ следующими уравнениями:
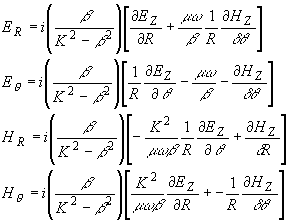 (6) (6)
Постоянная распространения b
определяется, характеристическим уравнением
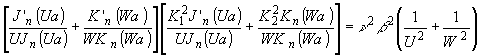 (7) (7)
- 94 -
где a - радиус жилы волокна и может принимать дискретный набор значений из интервала K22 £
b
2 £
К21.
Важным параметром моды является частота отсечки. Если частота световой волны меньше, чем частота отсечки моды, то такая мода не может распространяться по волокну. Существует одна мода, обозначаемая НЕ 11, для которой отсечка не существует. Это обстоятельство имеет чрезвычайно большое значение и позволяет создавать одномодовые оптические волокна. Условие одномодовости выглядит следующим образом:
2p
a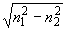 /l
< 2,405 (8) /l
< 2,405 (8)
Пусть l
= 1,0 мкм, n1-n2 = 10-3, такой порядок разности коэффициентов преломления жилы и оболочки типичен для волокон. В этом случае для одномодового режима необходимо, чтобы радиус жилы был меньше 7 микрон. Изготовить волокна с такой жилой достаточно просто.
В настоящее время рассматриваются, в основном, либо одномодовые волокна, либо волокна с очень большим числом мод, которые допускает геометрическое рассмотрение. Причем последние рассматриваются значительно чаще. Поэтому вернемся к геометрической оптике и рассмотрим уширение импульса при прохождении его по оптическому волокну.
В оптических волокнах уширение импульса обусловлено тремя причинами:
1. дисперсия материала, из которого изготовлено оптическое волокно.
2. Внутримодовая дисперсия. Которая отражает тот факт, что фазовая и групповая скорости волны, распространяющиеся в каждой моде, зависят от частоты света.
3. Межмодовая дисперсия, которая отражает тот факт, что групповые и фазовые скорости различных мод одного и того же волновода, различны.
В настоящее время для большинства волокон преобладающий вклад в уширение импульса дает межмодовая дисперсия. Рассмотрим оптическое волокно, на вход которого подается очень узкий импульс
- 95 -
света (рис.3)
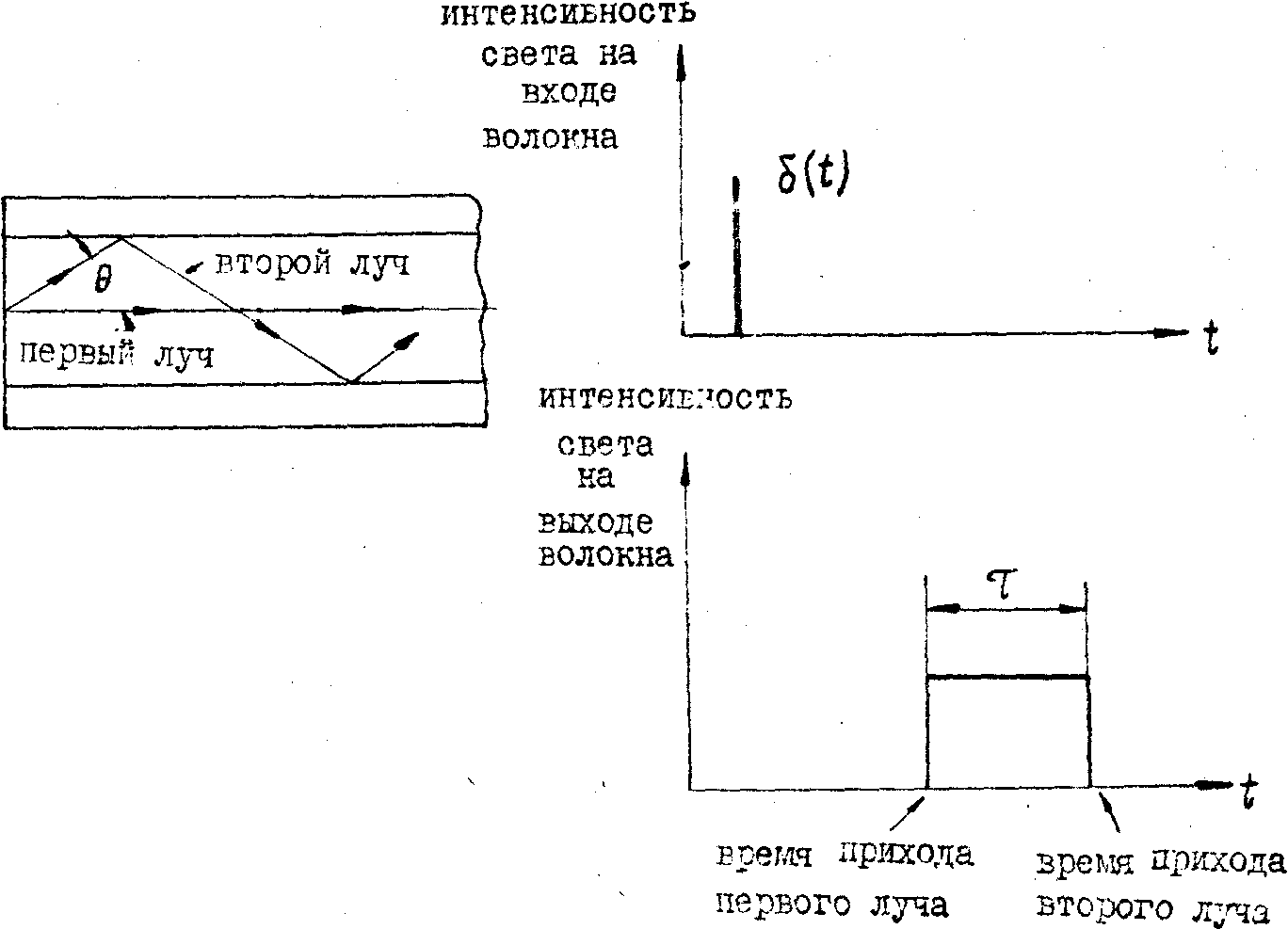
Рис.3. Уширение оптического импульса при прохождении по оптическому волокну.
Предположим, что этот импульс распространяется по волокну по всевозможным путям. Длина пути луча зависит от угла q
, под которым он распространяется по волокну. В соответствии с этим световые импульсы, распространяющиеся по волокну различными путями, достигнут выходного торца в различное время. В результате, вместо узкого входного импульса, на выходе будет более широкий импульс. Его длительность равна разнице во временя прихода самого быстрого и самого медленного импульса. Простейший подсчет с помощью формулы (3) показывает:
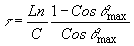 (9) (9)
- 96 -
где t
- ширина импульса на выходе волокна, L - длина волокна. Если D
n = n1-n2 малая величина, тогда угол q
max тоже мал и в первом приближении можно написать:
t
= L· А2/2cn 1 (10)
Обычно волокна имеют апертуру около 0,2, это дает уширение импульса порядка 50 нсек/км. При такой дисперсии максимально возможная полоса пропускания линии длиной 1 км равна 20 мгц.
Для уменьшения дисперсии были разработаны волокна с плавным изменением коэффициента преломления сердцевины,так называемые градиентные волокна (рис.4).
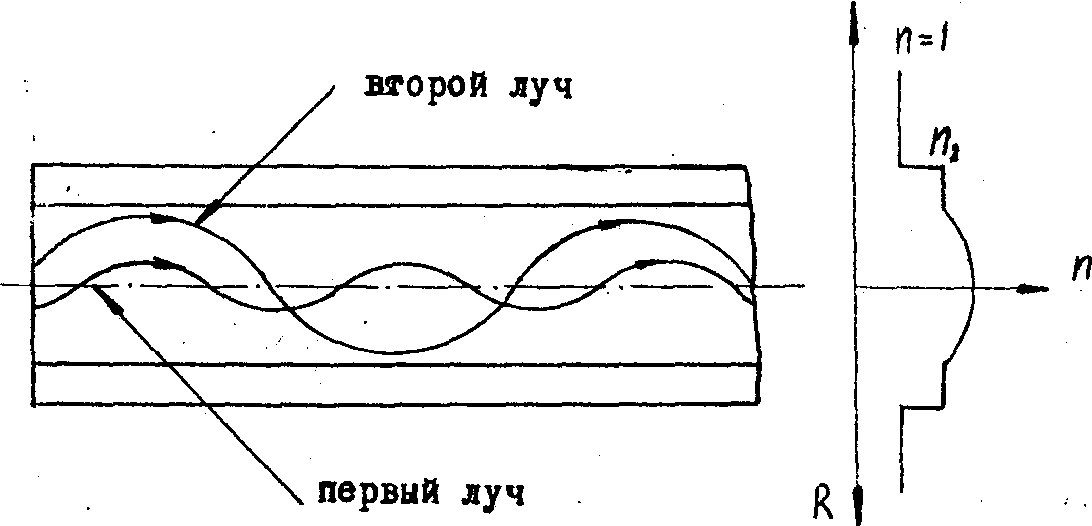
Рис.4. Распространение света по градиентному волокну.
Физический смысл их работы можно понять, рассмотрев два луча. Один луч движется все время вблизи центра волокна, второй же совершает около оси волокна колебания с большой амплитудой. Очевидно, что геометрические пути этих: лучей различны, однако, второй луч значительную часть времени проводит в среде с меньшим коэффициентом преломления. Это приводит к выравниванию оптических путей и уменьшению дисперсии. Расчет импульсного отклика волокна при произвольном профиле коэффициента преломления может быть проведен только численно. Однако, имеется важный в практическом отношении и допускающий точное решение класс профилей - так называемые a
- профили:
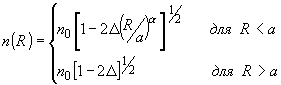 (11) (11)
- 97 -
a
- параметр, который может изменяться от 1 до ¥
.
Уширение импульсов в таком волокне было теоретически вычислено в работе. Оказалось, что в первом приближении по D
ширина импульса равна нулю при a
= 2, и вклад в уширение импульса дает только слагаемое второго порядка малости по D
. Таким образом, квадратичный профиль позволяет очень сильно уменьшить дисперсию волокна. Для других значений D
слагаемые первого порядка по a
не равны нулю и дисперсия значительно больше (напомним, что D
»
0,01) и определяется формулой
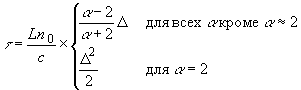 (12) (12)
В этой же работе было показано, что минимальное уширение будет происходить при a
опт = 2 - 2D
, что дает ширину выходного импульса
t
= Ln0D
2 /8с (13)
Рассмотрим, например, волокно, у которого D
= 0,01. При a
=2 дисперсия будет равна 0,15 нсек/км. При a
= 2 - 2D
дисперсия составит всего 0,04 нсек/км.
Второй вклад в уширение импульса дет дисперсия материала , из которого изготавливается волокно. Уширение за счет этого фактора зависит от ширины спектра источника света. Для светодиода с полосой излучения 300 и оно составляет по порядку величины 1 нсек/км. Для полупроводникового лазера с полосой 30 Å, ñоответственно, 0,1 нсек/км.
В настоящее время имеются сообщения об изготовлении градиентного волокна с очень малой дисперсией /6,7/ в этих работах описывается изготовление и исследование волокна с дисперсией 0,26 нсек/км.
Такая величина была достигнута при a
= 1,8 и разности коэффициентов преломления между центром жилы и оболочкой, равной 0,0067. Для сравнения можно сказать, что волокно со ступенчатым
- 98 -
профилем коэффициента преломления имело бы дисперсию около 20 нсек/км, что примерно в 75 раз больше.
Наименьшей дисперсией обладают одномодовые волокна ,поскольку в них совершенно отсутствует межмодовая дисперсия. Вопрос о дисперсии в таких волокнах детально исследовался в работе Глота /3/. Его расчеты показывают, что основной вклад в уширение импульса дает дисперсия материала. Это перестает быть верным для волокон из кварцевого стекла на длинах волн порядка 1,4 мкм. В этой области дисперсия кварцевого стекла близка к нулю и становится сравнимой с внутримодовой дисперсией /8/.
Другой важнейшей характеристикой оптического волокна, наряду с дисперсией, является величина затухания света в волокне. Существует несколько причин, приводящих к затуханию света. Основные из них следующие:
1. поглощение света за счет примесей ионов;
Основную роль здесь играют ионы металлов переходной группы и ионы гидроксильной группы ОН¾
;
2. рассеяние за счет несовершенства границы оболочка-жила.
Соотношение между потерями за счет различных факторов изменялась по мере совершенствования технологии изготовления волокна. Первые волокна имели затухание порядка 1000 дб/км и основной причиной было наличие примесей. За последние годы удалось получить волокна из чрезвычайно чистого стекла. В таких волокнах основной причиной затухания света является рэлеевское рассеяние. Характерной особенностью его является быстрое уменьшение с увеличением длины волны, обратно пропорционально 4й степени l
. В настоящее время наименьшие потери 0,47 дб/км, получены на длине волны 1.3 мкм /8/.
Уменьшение затухания и уменьшение дисперсии являлись основными направлениями в развитии волоконной оптики в последнее десятилетие. Успех этих работ позволил говорить о создании реальных , экономически эффективных волоконно-оптических линий связи.
Однако, помимо использования в обычных волоконно-оптических линиях связи, оптическое волокно может найти применение и в других устройствах. Например, оно может быть использовано в качестве дисперсионной линии задержки для сжатия частотно-модулированных (ЧМ) оптических импульсов. Эффект сжатия ЧМ сигналов хорошо
- 99 -
известен в радиотехнике /9/. Он заключается в том, что, если на вход дисперсионной линии задержки подается ЧМ сигнал в виде импульса длительностью t
с, то на выходе возникает короткий импульс длительностью t
b = t
c/Kсж, где Ксж - коэффициент сжатия характеризует степень уменьшения длительности входного импульса. Сжатие может в значительной степени уменьшить влияние помех, которые поступают на вход дисперсионной линии задержки вместе с полезным сигналом, поскольку при сжатии амплитуда сигнала увеличивается по порядку величины в Ксж раз, амплитуда же помех остается неизменной. Тем самым достигается значительное увеличение соотношения сигнал/шум.
Пусть на вход одномодового волокна подается ЧМ сигнал вида
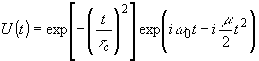 (14) (14)
t
с - постоянная определяющая ширину импульса, m
= ¶
w
/¶
t - скорость изменения угловой частоты.
Определим параметры оптического волокна, которые необходимы для сжатия сигнала вида (14). Для того, чтобы найти сигнал на выходе волокна, необходимо перемножить спектры входного сигнала и частотную характеристику оптического волокна, и затем взять обратное Фурье-преобразование.
Частотную характеристику волокна возьмем в виде
g(w
) = exp[-ib
(w
)z] (15)
где z - длина волокна, b
- постоянная распространения. Это означает, что мы пренебрегаем зависимостью затухания в оптическом волокне от длины волны в берем в расчет только задержку по фазе.
Спектр входного сигнала равен
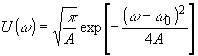 (16) (16)
где 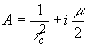 . .
Таким образом, сигнал на выходе волокна длиной z будет иметь
- 100 -
вид:
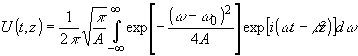 (17) (17)
В формулу входит b
(w
). Вид этой функции может быть весьма сложным. Однако, оптические ЧМ импульсы имеют обычно небольшой по сравнению с w
0 спектр. Поэтому можно разложить b
(w
) в ряд, сохранив только три первых члена:
b
(w
) = b
0 + b
1(w
- w
0) + b
2(w
- w
0)2 (18)
После этого интеграл (17) вычисляется, и мы можем легко получить все интересующие нас результаты. Основные из них следующие.
1. Максимальный коэффициент сжатия, который может быть получен при оптимальном выборе всех параметров.
Ксж = t
с/t
b = t
2c·m
/2 (19)
2. Для получения максимального коэффициента сжатия необходимо иметь волокно длиной
Z опт = 1/2b
2m
= t
2с/4b
2Ксж (20)
Обе формулы получены при условии, что
D
w
·t
с >> 1 (21)
где D
w
- девиация частоты входного сигнала.
Таким образом, волокно как дисперсионную линию задержки, характеризует, например, b
2. Остановимся на этом вопросе и дадим некоторые численные оценки. Как уже упоминалось, дисперсия в одномодовом волокне определяется двумя факторами: дисперсией материала и внутримодовой дисперсии моды НЕ11, причем преобладающий вклад вносит дисперсия материала. В этом случае выражение для коэффициента b
2, млеет вид:
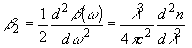 (22) (22)
- 101 -
Данные о значении величины d2n/dl
2 имеются в литературе. Для кварцевого стекла, например, они приведены в обзоре /3/. Воспользовавшись ими, получим, что для кварцевого стекла на длине полны l
= 0,63 мкм, b
2 = 3·10-26 сек2/м.
Рассмотрим сжатие ЧМ оптических импульсов с параметрами, характерными для устройств сжатия, имеющихся в настоящее время /10/. Пусть t
с = 10-10 сек, Ксж=30. Тогда, согласно формуле (20), потребуется волокно длиной 3 км. Волокно такой длины можно наметить на небольшую катушку,тогда как в упоминавшейся работе /10/ сжатие осуществлялось с помощью двух дифракционных решеток, разнесенных на 29 метров.
В заключение кратко рассмотрим методы получения ЧМ оптических импульсов. В настоящее время в устройствах сжатия оптических импульсов используются, в основном, два способа. Один основан на использовании нелинейных эффектов при прохождении импульса мощностью несколько сотен мегаватт через вещество, в котором скорость распространения света сильно зависит от интенсивности света, например, через С S2 /10/.
Второй способ основан на использовании электрооптических кристаллов. Несмотря на то, что этот способ является весьма удобным и эффективным, в литературе отсутствует анализ возможностей таких модуляторов. Мы приведем оценку максимально возможного коэффициента сжатия, который могут обеспечить электрооптические модуляторы. Принцип работы их заключается в следующем. Свет, проходящий через кристалл, у которого показатель преломления изменяется под действием приложенного внешнего электрического поля Е, претерпевает изменение фазы
D
j
= D
j
0 + 2p
D
nx/l
(23)
здесь х - длина оптического пути в кристалле, D
n = a
·Е. Будем считать, что поле приложено вдоль оси Х и изменяется во времени по закону
E = a0t2 (24)
В этом случае с учетом (23) получим:
- 102 -
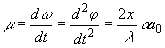 (25) (25)
Учтем, что изменение Е может производиться в пределах, ограниченных пробивным значением Епр. Это накладывает ограничение на максимальную длительность импульса t
с. При этом максимальный коэффициент сжатия будет равняться
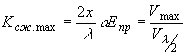 (26) (26)
где Vmax = Епр·х - максимально возможное напряжение на кристалле, 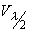 - полуволновое напряжение, напряжение при приложении которого к кристаллу наблюдается сдвиг фазы световой волны на p
. - полуволновое напряжение, напряжение при приложении которого к кристаллу наблюдается сдвиг фазы световой волны на p
.
Таким образом, предельный коэффициент сжатия зависит только от размеров и электрооптических свойств кристалла. Например, для LiNBО3 полуволновое напряжение равно 2000 В, а напряжение пробоя 100 кВ/см, что позволяет на кристаллах размером 1 см получить Ксж = 50.
Литература
1. "Fundamentals of Optical Fiber Communications", edited by Michael K.Barnoski, Academic Press, New York, 1973
2. Д.Маркузе. "Оптические волноводы", М., 1974.
3. С.Миллер и др. "Исследование световодных систем связи", ТИИЭР, 61, 46-104, 1973.
4. A.V.Snyder, "Leaky-Ray Theory of Optical Waveguides of Circular Crss Section", Appl.Phys. v.4, p.273-298. (1974).
5. D.Gloges, E.A.I.Marcatili, "Multimode Theory of Graded Core Fibers", BSTJ, v.52, p.1563-15. (1973).
6. W.G.French, G.W.Tasker, I.R.Simpson, "Graded index fiber Wave Guides with Borosilicate Composition; Fabrication Techniques", Appl.Opt., v.15, p.1803-1307, (1976).
- 103 -
7. L.G.Cohen, "Pulse Transmission Measurements for Determining Hear Optimal Profile Gradings In Multimode Borosilicate Optical Fibers", Appl.Opt., v.15, p.1808-1814. (1976).
8. Tansuya Kimura, Kazuhiro Daikoku, "Proposal on Optical Fibre Transmission Systems In a Low-loss 1,0-1,4 Wavelength Region", Opt. & Quant.Electron., v.9, p.33-42 (1977).
9. Я.Д.Ширман. "Разрешение и сжатие сигналов", М., 1974.
10. R.H.Lehmberg & J.M.McMahon, "Compression of 100-psec Laser Pulses", Aрр1. Opt., v.28, p.204-206. (1976).
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

