ПРИМЕНЕНИЕ ГОЛОГРАФИЧЕСКОЙ И СПЕКЛ-ИНТЕРФЕРОМЕТРИИ ДЛЯ ОПРЕДЕЛЕНИЯ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ЭЛЕМЕНТОВ КОНСТРУКЦИЙ, ДЕФЕКТОСКОПИИ И ДЕФЕКТОМЕТРИИ

А.А.Рассоха

Аннотация

Приводятся общие результаты исследования напряженно-деформированного состояния, дефектоскопии и дефектометрии элементов конструкций с помощью голографической и спекл-интерферометрии. Обсуждаются особенности методов, совмещающих голографическую и спекл-интерферометрию.

Определение напряжённо-деформированного состояния (НДС) элементов конструкций сложной конфигурации расчётными методами часто бывает затруднительно и вынуждает использовать расчётные модели, не вполне адекватные исследуемому элементу. Решающее слово в таких случаях принадлежит эксперименту.

Большинство практически важных задач сводится к оценке гладкого "фона" подя напряжений и более точному определению напряжений в областях их концентраций. Применение голографической и спекл-интерферометрии позволяет получать значения перемещений произвольных точек элемента конструкции, однако Для определения поля напряжений вблизи концентраторов использование результатов эксперимента целесообразно совмещать с расчётными методами.

Запишем дифференциальное уравнение теории упругости в виде /1/

- 97 -

Divh(F,x) + r _æb = 0 (1)

с граничными условиями в перемещениях:

x_æ(х) = ¦ (х) (2)

и усилиях.

T_æ(x)n_æ = j (x), x Î ¶ _æ(B) (3)

где:

В - исследуемое тело; æ - его отсчетная конфигурация, х_æ - поле перемещений, n_æ - орт нормали к границе, ¶ _æ - граница области c , Т_æ - тензор напряжений, r c - плотность, b - распределенная массовая нагрузка, F = Ñ c _æ - градиент перемещений, h- оператор физического закона, j ,¦ - заданные функции, x - координаты материальной точки в отсчетной конфигурации тела В.

Пусть выполнены условия единственности, и задача (1) - (3) имеет решение:

х_æ(x) = x (x), х Î æ(B) (4)

Тогда

x_æ(х) = x (х), х Î ¶ w , w Ì æ(B) (5)

и, в силу (1),

Divh(F,x) + r _æb = 0, x Î w (6)

решение задачи (6) с граничными условиями (5) совпадает с решением задачи (1) - (3), если оно единственно.

Таким образом, взяв в качестве w область вблизи концентратора и экспериментально определив граничные условия в перемещениях на ¶ w , можно найти поле напряжений вблизи концентратора решением задачи (6) на области w . Поскольку в действительности определяются перемещения не на всем контуре ¶ w , а в дискретном множестве точек, то густоту этих точек

- 98 -

целесообразно выбирать так, чтобы погрешность аппроксимации граничных условий по контуру была величиной того же порядка, что и погрешность эксперимента.

Аналитическое решение задачи (6) возможно лишь в немного — численных специальных случаях. Для реальных элементов конструкций необходимо использовать численные методы.

В случае, когда границы области w являются координатными линиями в некоторой системе координат с ортогональным базисом, наиболее эффективным методом решения является метод конечных разностей' /2/. Уравнение (6) аппроксимируется разностной схемой:

L_h(c u ) + r u bu = 0 (7)

где L_h - разностный оператор, u - индекс узловой точки;

c u =c _æ(xu ), r u = r _æ(xu ), bu = b(xu )

Граничные условия (5) преобразуются к виду:

c u = x (хu ), хu Î ¶ w (8)

Задача (7) имеет единственное решение в подавляющем большинстве практически важных случаев; кроме того, погрешность решения, вызванная неточностью задания граничных условий (8.) затухает на удалении от ¶ w , если существует норма в пространстве решений, такая, что /3/

║D c u ║ £ C║D x u ║ (9)

где D c u - возмущение решения, D x u - возмущение граничных условии. С - константа, не зависящая от D x u .

Численное решение на произвольной области w можно получить методом конечного элемента. Соотношение (9) хорошо выполняется при этом для многих типов элементов.

Воспользуемся тем, что уравнение (6) представляет собой условие стационарности функционала /4/

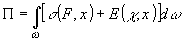(10)

где скаляры s и Е удовлетворяют выражениям;

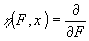r _æs (F,x) (11)

- 99 -

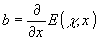(12)

Введением конечноэлементной аппроксимации поля перемещений определим функционал П как функцию перемещений внутренних узлов области w при заданных перемещениях граничных узлов и нейдем минимум П из условий:

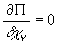
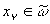(13)

где 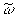- внутренность области w .

Следует отметить, что совмещение экспериментальных и рас -четных методов исследования НДС элементов конструкций позволяет повысить достоверность получаемых результатов по сравнению с обоими этими видами исследования: с одной стороны, вследствие прямого использования экспериментальных данных улучшается адекватность расчета реальному элементу конструкции, с другой - использование теоретической расчетной модели уменьшает влияние ошибок эксперимента, вызванных случайными дефектами образца и погрешностью измерений, в частности, позволяет объективно решить проблему сглаживания экспериментальных точек.

Для рассмотрения возможных вариантов решения обратных задач с применением спекл-интерферометрического исследования НДС твердых тел запишем выражение (1) в координатной форме:

Aa _mKb c ^k_{æ,a ,b} + r _æb_m = -q_m (14)

где

Aa _mKb º 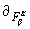h a _m (15)

q_m = 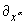h a _m (16)

c ^k_{æ,a ,b} - вторая ковариантная производная. В частности, в прямоугольных декартовых координатах

c ^k_{æ,a ,b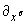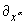} = c ^K_m(xd ,t) (17)

- 100 -

Поскольку для однородных, на макроуровне, тел q_m =0 ,то решение прямой задачи в случае однородного тела удовлетворяет условию

A(F,x) + r _æ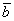 =0 (18)

откуда видно, что наличие неоднородности равносильно приложению дополнительной нагрузки q_m в области изменения тензора упругости. Для линейно-упругого материала

q_m = (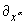Aa b _mk)F^kb (19)

в частности, для изотропного линейно-упругого материала в случае плоского напряженного состояния

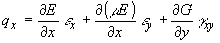(20)

где 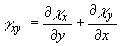- угловая деформация, или, считая коэффициент Пуассона m постоянным (что характерно для геометрических неоднородностей),

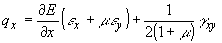(21)

или в напряжениях:

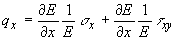(22)

Считая, что ось x совпадает с направлением градиента Е, найдем, что возмущающее влияние неоднородности максимально, когда она совпадает с первой главной осью тензора напряжений:

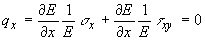
если s _x = 0; следовательно, приложение нагрузки в направлении линейного дефекта не дает возможность обнаружить его по измене -шло напряженно-деформированного состояния.

Подстановкой экспериментально найденных значений перемещений в (14) можно получить решение для поля физического закона Аa b _mk(x), однако такой метод чувствителен к ошибкам эксперимента и не вполне устойчив вычислительно.

- 101 -

Для количественной оценки параметров дефекта более целесообразным является подход, основанный на применении метода конечного элемента и минимизации невязки экспериментальных данных и теоретического решения. В качестве примера рассмотрим задачу дефектометрии плоского образца, имеющего местное утоньшение.

Предположим, что дефект локализован методами дефектоскопии. Нанесем конечноэлементную сетку на область возмущения решения. Пусть из эксперимента известны перемещения узловых точек. Считая толщину постоянной в пределах группы соседних элементов, запишем уравнения равновесия их узлов:

c^Id + t^IId = R (23)

где c^I - суммарная матрица жесткости элементов, не входящих в группу;

c^II - суммарная матрица жесткости элементов.входящих в группу, при их единичной толщине,

t^II - толщина этих элементов;

d - перемещения узлов.

ВЬбрав в качестве невязки квадрат нормы вектора невязок правых частей, из условия ее минимума получим толщину внутренних элементов:

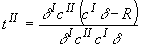(24)

Последовательным итерационным повторением этих вычислений найдем распределение толщин во всей области дефекта. Выражения в числителе и знаменателе формулы (24) неотрицательны вследствие неотрицательной определение ста матриц жесткости; знаменатель, однако, может быть близок к нулю, если деформации внутренних элементов малы, что необходимо учитывать при выборе разбивки области.

Эффективность сочетания голографической и спекл-интерферометрии с методом конечного элемента, реализованным нами в комплексе программ для ЭВМ типа ЕС подтвердилась при подробном исследовании напряженно-деформированного состояния лопатки и диска турбины авиационного двигателя, поршня двигателя

- 102 -

внутреннего сгорания, соединения элементов из углепластика, а также при дефектоскопии элементов конструкций из композиционных материалов.

Схемы экспериментов собирались на базе установки СИН и ОКГ, ЛГ-38. Голограммы двойной экспозиции получали по схемам с наклонным и встречным опорным пучком. Перемещения и поворот исследуемой области как абсолютно-твердого тела относительно фотопластинки, существенно снижающие точность измерения деформаций, устранялись закреплением регистрирующей фотопластинки на исследуемой части объекта /5/. При получении голограмм двойной экспозиции с наклонным опорным пучком смещения и поворот исследуемой области относительно фотопластинки как целого устранялись соответствующими смещениями и поворотом фотопластинки в своей плоскости между двумя экспозициями после нагружения объекта. Величина смещений исследуемой области как целого определялась по показаниям микрометрических индикаторов, установленных в плоскости объекта.

Интерференционные картины, полученные с голограмм двойной экспозиции, использовались для качественного исследования возникающих полей деформаций и концентрации напряжений. Количественная расшифровка голограмм двойной экспозиции, полученных по схемам с наклонным и встречным опорным пучком, осуществлялась с помощью спекл-интерферометрии. Для получения спекл-интерферограмм с голограмм двойной экспозиции применялись схемы, предложенные в наших работах /5,6/.

Литература

1. К.Трусделл. Первоначальный курс рациональной механики сплошных сред, стр.592, М., "Мир", 1975.

2. А.Л.Квитка, П.П.Ворошко, С.Д.Бобрицкая. Напряженно-деформированное состояние тел вращения, стр.208, Киев,"Наукова думка", 1977.

3. O.K.Годунов, В.С.Рябенький. Резонансные схемы, стр.439, М.. "Наука",1977.

4. Дж.Оден. Конечные элементы в нелинейной механике сплошных сред. стр.464, М., "Мир", 1976.

- 103 -

5. А.А.Капустин, С.0.Мажура, А.А.Рассоха. Сб. "Новые физические методы неразрушающего контроля качества продукции", стр.11-18, М., МДНТП, 1977.

6. К.Г.Гусев, А.А.Капустин, А. А. Рассоха. Материалы IX Всесоюзной школы по голографии, стр.267-286, Л., ЛИЯФ, 1977.