|
|
 |
 |

|
| |
ИНВАРИАНТНОСТЬ К МАСШТАБУ И ПОВОРОТУ ВХОДНОГО СИГНАЛА В ГОЛОГРАФИЧЕСКИХ УСТРОЙСТВАХ РАСПОЗНАВАНИЯ
А.Л.Ауслендер, Г.Г.Левин
В статье рассмотрены алгоритмы обработки изображений в системах распознавания, при которых реализуется инвариантность корреляционной функции к масштабу и повороту входного сигнала. Рассмотрены также оптико-электронные схемы, реализующие эти алгоритмы.
Одним из основных факторов, сдергивающих широкое распространение когерентно-оптических систем распознавания и идентификации изображений, является неинвариантность решающей функции к изменениям (гомотетии) масштаба и поворота (движения) входного сигнала (см., например, /1/ ).
Преобразования движения и гомотетии образуют четырехпараметрическую группу афинных преобразований Н 4, которая описывается выражением:
x' = a
(xCosq
- ySinq
) + x
; y' = a
(xSinq
+ yCosq
)+ h
(1)
где a
- параметр гомотетии;
q
- угол поворота;
x
, h
- параметры трансляция (смещения).
Зависимость корреляционной функции от a
и q
следует из свойств Фурье-преобразования. Действительно:
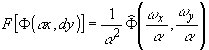 ; F[ ; F[
Ф(x',y')] = 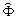 (w
'x,w
'y) (w
'x,w
'y)
- 71 -
w
'x = w
xCosq
- w
ySinq
; w
'y = w
xSinq
+ w
yCosq
здесь Ф и  - изображение и его Фурье-образ, соответственно. - изображение и его Фурье-образ, соответственно.
Известен целый ряд способов и оптико-электронных схем, которые в той или иной степени позволяют решать эту задачу.
К первой группе способов обеспечения инвариантности можно отнести методы мультипликации изображений (либо фильтров) в пространстве или во времени.
Типичным примером схемной реализации метода мультипликация во времени является схема Вьено /2/, в которой голографический фильтр устанавливается в обойму револьверной головки и вращается с помощью электродвигателя. Корреляционная функция формируется на мишени телевизионной камеры, причем время полного оборота фильтра согласовано со временем накопления заряда на мишени трубки. Основным недостатком этого способа является малое быстродействие и наличие вибраций системы.
При мультипликации анализируемого изображения в пространстве в /3/ недостатком является необходимость наличия большого числа каналов, используемых для записи эталонов с различной ориентацией и масштабом, что сужает класс анализируемых изображений.
В работе /4/ рассмотрена схема мультипликации входного изображения, основанная на применения оптических систем о обратной связью (см.рис.1).
Луч лазера 1 расширяется коллиматором 2, 3 и освещает изображение, которое, фокусируясь объективом 4 через светоделительный клин 5, вводится в замкнутую оптическую систему, состоящую из объективов 6, 7 и плоских зеркал 8, 9, между которыми помещается система поворота изображения 10 (призма, система зеркал). Часть светового потока отражается от светоделителя 5 и возвращается в замкнутую систему, а прошедший через светоделитель световой поток фокусируется объективом в плоскости голографического фильтра. Объектив 11 формирует корреляционное поле в плоскости считывания. Если в замкнутой части системы произвести изменение масштаба (например, при использовании разнофокусных объективов 6,
- 72 -
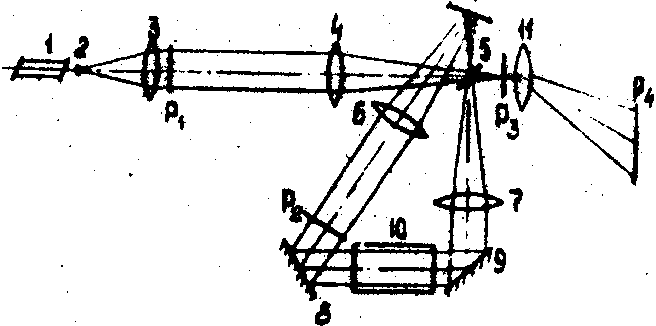
Рис.1 . Схема для выполнения афинных преобразование изображения
1 - лазер; 2, 3 - коллиматор, Р1 - анализируемое изображение, 4 - объектив; 5 - светоделительный клин; 6, 7 - объективы; 8, 9 - плоские зеркала; 10 - система поворота изображения; 11 - объектив; P2 - фурьер-плоскость; Р3 - выходная плоское.
7) или разварить изображение зеркалами 8, 9, то (формулируется последовательность равномасштабных изображений или последовательность разноориентированных изображений.
В работ показано, что, используя серийные оптические элементы (зеркала, светоделители, линзы), можно получить мультипликацию на 50 каналов.
Ко второй обширной группе способов обеспечения инвариантности система распознавания можно отвеете различные виды разверток рецепторного поля.
- 73 -
Для получения изображения инвариантного к масштабу и повороту достаточно съем информации осуществлять с помощью радиально-круговой развертки. Причем ее начало выбирается в центра тяжести изображения. На рис.2 /5/ приведено изображение 3-х квадратов (а) и характеристические контуры функции (ХКФ) (б), подученные в результате радиально-круговой развертки. Из рис.2 видно, что поворот изображения приводит к смещению ХКФ по оси i, а масштаб в смещению по оси X.
 
а) б)
Рис.2. Радиально-круговое сканирование изображения.
Инвариантность к перемещениям (вращение и трансляция) может быть достигнута при помощи случайного скопирования изображения. В /6/ показано, что' если дана функция Ф(х,у), где х = x(t), y = у(t) - стационарные в стациоварносвяванные случайные процессы с равномерным распределением, и вектор с составляющими х и у обладает равномерным распределением, то вероятностные характеристики Ф(t) не зависят от вращения в параллельного переноса функции Ф(х,у).
Из этого положения следует, что подобное квазислучайное сканирование -позволяет преобразовать входное изображение таким образом, что его автокорреляционная функция не зависит от движения в поде экрана.
Эффективным способом достижения инвариантности распознавания
- 74 -
при изменения масштаба входного изображения является варьирование скорости развертки рецепторного поля, с последующим анализом решающей функции.
Способы, используйте различные законы развертки, находят широкое применение в когерентных оптико-электронных системах распознавания образов. Это объясняется тем, что ввод в подобные система распознавания осуществляется через различные пространственные модуляторы света /1/. При этом сигнал либо непосредственно преобразуется из электрического в световое (электронно-лучевой модулятор света - ЭЛМС), либо при помощи сканирующего устройства из некогерентного в когерентный.
В /7/ описана схема оптико-электронного многоканального корреляторе, использующего для инвариантности к масштабу переменную скорость развертки изображения.
Способы, использующие различные законы развертки рецепторного поля, не уменьшают полноту описания входных изображений. Однако, можно указать на целый ряд преобразований исходного изображения, которые позволяют определить инварианты к гомотетии и повороту. Одной из наиболее развитых моделей распознавания изображений, является модель, использующая моменты инварианты .
Двумерными моментами (р +q)-го порядка от функции Ф(х,у) описывается выражение - mpq:
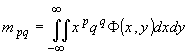 , p,q = 0, 1, 2 ... (2) , p,q = 0, 1, 2 ... (2)
Положим параметры трансляции в выражении (1) равными 0. Тогда преобразование гомотетии можно записать в виде:
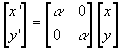 (3) (3)
Из (3) по теореме Ху [8] следует: m'pq = a
p+q+2mpq.
- 75 -
Отсюда нетрудно получить инвариант гомотетии:
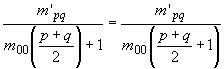 , p+q = 2, 3, … (4) , p+q = 2, 3, … (4)
Поворот изображения ва угол может быть представлен в виде:
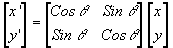 (5) (5)
Подставив в (5) выражения для моментов второго порядка, после ряда упрощений, можно получить следующую связь моментов повернутого изображения с исходным:
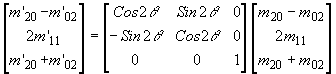 (6) (6)
Из уравнения (6) нетрудно получить инварианты вращения:
m'20 + m'02 = m20 + m02; (m'20 – m'02)2 + 4(m'11)2 = (m20 – m02)2 + 4m11
Соотношения (4) и (7) могут быть непосредственно использованы для опознания изображений независимо от масштаба в ориентация.
Нетрудно заметить, что моменты являются коэффициентами рада Тейлора Фурье-образа анализируемого изображения.
Принципиальная схема, реализующая распознавание с использованием моментных инвариантов, изображена на рис.3. Транспарант с изображением освещается когерентный излучением, мультиплицируется, и в задней фокальной плоскости линзы Л формируется набор
-76-
спектров. В эту же плоскость помещается набор амплитудно-фазовых масок, которые позволяют вычислить моменты Фурье -образа, инвариантного к сдвигу изображения. Линзовый растр фокусирует свет после матрицы масок в матрицу фотоприемников, после которое значения моментов поступают в блок зачисления моментных инвариантов. Для сравнения с моментными инвариантами эталонных изображений используется когерентный оптический многоканальный коррелятор.
Моделирование на ЭВМ такого оптико-электронного коррелятора показало, что использование только моментов второго порядка не дает высококачественных результатов при числе градации в моменте ~ 10. Необходимо либо существенно повышать число градаций, либо увеличивать число инвариантов.
Дня построения инвариантов гомотетии и вращения могут бить использованы и другие представления изобретения. В частности, для определения инвариантов используется радиальное и секторное преобразование изображения, которое описывается выражениями:
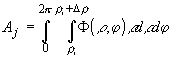 ; ; 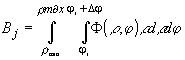 (8) (8)
Нетрудно показать /9/, что набор чисел А и В образуют достаточно полное описание изображения и инвариантен к его масштабу в повороту.
Некоторой модификацией этого метода может служить метод построения обобщенных признаков, описанный /10/. Например, в качестве инвариантов к повороту в /10/ предлагается использовать разложение Ф(х,у) в ряд по функциям Бесселя:
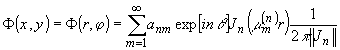 (9) (9)
где J n - функция Бесселя n20 порядка, m
(n)m – m – u' корень Т ║Jn║ - норма.
- 77 -
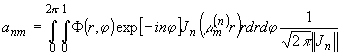
Для повернутого на угол q
изображения:
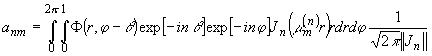
Нетрудно заметить, что
anm(q
= anm(0)exp[-inq
]
т.е. модули коэффициентов ряда (9) инвариантны к повороту изображения.
Оптические схема, реализующие радиальное и секторное преобразования изображений, в принципе, схожи со схемой на рис.3 и подробно описаны в целом ряде работ /11,12/.
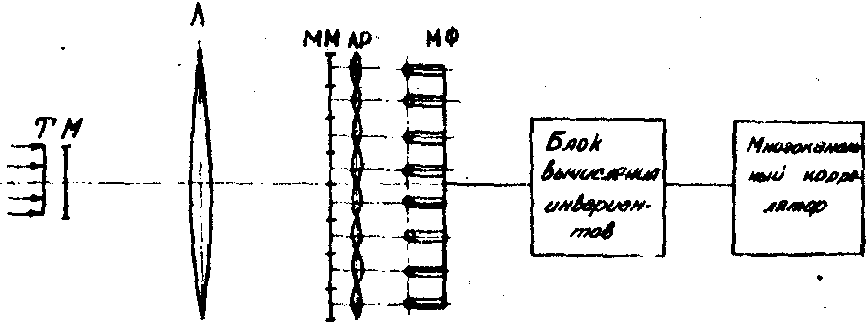
Рис.3. Принципиальная схема, реализующая распознавание с использованием моментных инвариантов.
Одним из способов реализация голографических инвариантных корреляторов является построение оптико-электронных систем,
- 78 -
осуществляющих новые типы преобразований. Рассмотрим наиболее интересное преобразование Меллина, определяемое выражением:
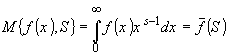 ; S = s
+ it
(10) ; S = s
+ it
(10)
Из (10) легко получить свойство этого преобразования:
M{¦
(ax),S} = a-SM{¦
(x),S}; a > 0 (11)
Это свойство показывает, что образы Меллина функций, отличающихся масштабом, различаются лишь наличием степенной функция.
Преобразование Меллина для обработки изображений впервые было использовано в системах цифровой фильтрации /13/.
Используя данные работы /13/, нетрудно показать, что, если изображение Ф(r,q
) повернуто на угол q
0 и изменено по масштабу на a
, то последовательное применение преобразования Меллина (по r) и Фурье (по q
) дает возможность получить инвариантный MrFq
- образ. Действительно:
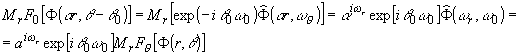
т.е. |
MrFq
[Ф(a
r,q
-q
0)]|
= a
|
MrFq
[Фr,q
)]
В работе /13/ показана возможность реализации преобразования Меллина в Фурье-процессоре. Действительно, нетрудно показать, что, произведя в выражении (11) замену переменных х = ехрx
, получим при S= -i2p
u
- 79 -
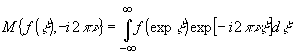
Таким образом, преобразование Меллина функции ¦
(х) можно легко получить, вычислив преобразование Фурье от функция ¦
(еxpx
).
В работе /1/ предложена следующая схема построения пространственно-масштабных (ПМ) инвариантных корреляционных оптико-электронных систем. Пусть Ф1 - эталонная функция, а Ф2 - анализируемая функция, тогда алгоритм построения разбивается на 4 этапа (изготовление фильтра (Ф1) и преобразование входной функция (Ф2) рассматриваются одновременно).
1. Формируются модули |
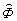 1|
и | 1|
и |
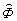 2|
. Этим достигается инвариантность к сдвигу. 2|
. Этим достигается инвариантность к сдвигу.
2. Проводится переход к полярным координатам |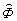 1(r,q
)|, | 1(r,q
)|, |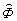 2(r,q
)|. Этим достигается инвариантность к повороту. 2(r,q
)|. Этим достигается инвариантность к повороту.
3. Масштаб по r преобразуется По логарифмическому закону:
|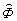 1 1 (еxpr,q
)|, |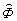 2(ехрr,q
)| 2(ехрr,q
)|
4. Осуществляется преобразование Фурье от функция |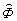 1(ехрr,q
)|, | 1(ехрr,q
)|, |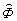 2(ехрг,q
)|
, что эквивалентно преобразованию Меллина от | 2(ехрг,q
)|
, что эквивалентно преобразованию Меллина от |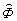 1(г,q
)|, | 1(г,q
)|, |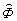 2(r,q
)|
. В результате получается ПМ - инвариантное преобразование. 2(r,q
)|
. В результате получается ПМ - инвариантное преобразование.
Этапы 1 и 4 выполняются линзами. Этапы 2 и. 3 могут, быть выполнены либо с помощью масок, синтезированных на ЭВМ /14/, либо специализированными оптико-электронными преобразователями, что приводят к существенным трудностям оря построении подобных систем.
В конце можно отметить еще один метод, использующий предопознавание информационных фрагментов изображения, который позволяет анализировать изображения с более сложными преобразованиями. На ЭВМ эти методы широко используются. Достаточно назвать структурнолингвистический метод /15/, непрерывно-групповой /16/ и т.д. Однако их реализация в оптико-электронном процессоре достаточно
- 80 -
сложна и в настоящее время неизвестна публикации с описанием подобных систем.
Л и т е р а ту р а
1. Д.Кейсесент, ТИИЭР, т.65, № 1, стр.92-100, 1973.
2. Ж-Ш Вьено и др. "Оптическая голография. Развитие и применение", "Мир", М., 1973.
3. Г.И.Василенко. "Голографическое распознавание образов", "Сов.радио", М., 1977.
4. Е.С.Нежевенко, Б.И.Спектор. "Автометрия", № 6, стр.14-18, 1976.
5. В.И.Васильев, В.Е.Реуцкий. "Автоматика", № 2. стр.27-32, 1967.
6. В.И.Васильев. "Распознающие системы", "Наукова думка", Киев, 1969.
7. А.Л.Ауслендер в др. 'Топографические методы и аппаратура, применяемая в физических исследованиях", науч. тр. ВНИИФТРИ, М., 1976.
8. M.K.Hu, IRE Trans., IT-8, N 2, р. 123-130, 1962.
9. G.G.Ledakis, G.L.Stanley, Proc. of the IEEE, v 58, p.192-216, 1970.
10. В.М.Линкин. В сб. "Читающие устройства", ВИНИТИ, 1965.
11. А.Н.Титов и др.. В сб. "Проблемы голографии", вып.2, М., стр.190-195, 1973.
12. K.Tanaka, Pattern Recognition, N 4, р.251-262, 1972.
13. Г.Роббинс, Т.Хуанг. ТИИЭР, т.60, № 7, p.251-262, 1972.
14. O.Bryngdahl, JOSA, v.64, N 8, р.1092-1099, 1974.
15. Р.Нарасимахан. В сб. "Автоматический анализ сложных изображений". "Мир", М., стр.50-64, 1969.
16. В.С.Файн. "Опознавание изображений", "Наука", М., 1970.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

