МОДОВАЯ
ТЕОРИЯ ОБЪЕМНЫХ ГОЛОГРАММ, ч.ч. I и II
Б.Я.Зельдович,
В.В.Шкунов
Излагаются
основные представления модовой теории объемных голограмм.
Развита
модовая теория объемных голограмм, учитывающая векторный
характер электромагнитного поля. Собственные моды в задаче
со скалярной регистрирующей средой оказываются двукратно
вырожденными по поляризации восстанавливающего воля. На
основе этой теории найдены законы преобразования волн с
произвольным пространственно-неоднородным состоянием поляризации
объемными голограммами. Подробно рассмотрены два случая
записи: 1) опорная волна имеет широкий угловой спектр, и
2) оперная волна состоит из двух плоских волн с ортогональными
поляризациями. В обоих случаях определены величины "поляризационных
шумов" и дифракционной эффективности. Полученные выражения
для каждой конкретной задачи позволяют оптимизировать процессы
записи и восстановления. В частности, найдены условия на
опорные волны, для которых возможно полное восстановление
записывающего поля со всей его поляризационной структурой.
I.
ЗАПИСЬ ГОЛОГРАММЫ И СТРУКТУРА МОД С УЧЕТОМ СОСТОЯНИЯ ПОЛЯРИЗАЦИИ
Введение
В
последние годы значительно повысился интерес к объемным
голограммам. Это было обусловлено созданием новых светочувствительных
-
47 -
материалов,
которые позволили реализовать основные преимущества, даваемые
схемой записи в толстослойных (т.е. объёмных) голограммах.
В числе таких преимуществ - возможность получения дифракционной
эффективности порядка единицы, а также возможность подавления
части шумов при использовании опорной волны с широки угловым
спектром. Теория восстановления световых полей такими голограммами
строилась обычно в 1-м Борковском приближении рассеяния,
см. /1/. Однако такое приближение заведомо не позволяет
описать действие голограммы с высокой (~ 1) дифракционной
эффективностью. В этой связи в последние годы в работах
/2,3/, и особенно /4/, была сформулирована теория, которую
можно назвать "модовой" теорией распространения волн в объёме
голограммы. Аналогичные представления были независимо сформулированы
в работах /5-10/ в связи с другой задачей - объяснением
явления обращения волнового фронта света при его вынужденном
рассеянии назад /5/.
Согласно
этим представлениям, в объёме среды с пространственно-неоднородным
показателем преломления или поглощения (усиления). наведенным
"записывающим" полем (или полем "накачки" в задачах вынужденного
рассеяния), существуют определённые типы пространственно-неоднородных
волн, которые могут быть названы "модами". В рамках этой
теории преобразование светового поля при прохождении через
голограмму может быть описано в терминах разложения восстанавливающей
волны по системе "мод" с последующим распространением каждой
из этих мод со своей (вообще говоря, комплексной) фазовой
скоростью. На этом пути оказалось возможным вычисление дифракционной
эффективности объёмных голограмм /2-4/ а также перенесение
результатов теории обращения волнового фронта /9/ на задачу
о спектральной селективности просветных объёмных голограмм
/11,12/. В недавней работе /13/ было рассмотрено влияние
пространственной неоднородности состояния поляризации на
процесс обращения волнового фронта при вынужденном рассеянии.
С другой стороны, вопросы записи и восстановления состояния
поляризации в голографии обсуждаются уже довольно давно
/14-17/; однако соответствующая теория до сих пор строилась
либо для плоских голограмм, либо, в Борновском приближении,
для
-
48 -
голограмм
со специальными анизотропными регистрирующими средами.
В
настоящей работе, состоящей из двух частей, сформулирована
подовая теория записи и преобразования пространственно-неоднородного
состояния поляризации световых волн объёмными просветными
голограммами. Отметим, что в отличие от скалярной задачи
(т.е. задачи с пространственно-неоднородной поляризацией}
здесь перенесение теории явления обращения волнового фронта
/13/ на проблемы голографии оказывается более сложным и
приводит к качественно отличной структуре системы мод.
Интерес
к вопросу о записи и восстановлении полей с учётом состояния
поляризации связан ещё и с тем, что даже при записи голограмм
при помощи поляризованной опорной волны само поле объекта
является, как правило, частично-поляризованным.
2.
Общие уравнения модовой теории
Задачу
о распространении записывающего и восстанавливающего полей
в объёме голограммы будем решать в приближении параболического
уравнения, справедливого для волн, идущих вблизи центрального
направления Z; последнее будет считаться перпендикулярным
поверхностям голограммы. В этом приближении монохроматическое
световое поле может быть представлено в виде
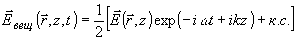 (1)
(1)
где двумерный
вектор  имеет компоненты
имеет компоненты
 = (х, у). В этом параксиальном
приближении комплексный вектор
= (х, у). В этом параксиальном
приближении комплексный вектор 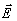 (
( ,z)
также имеет только поперечные компоненты
,z)
также имеет только поперечные компоненты 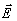 (Ex,Ey).
Записывающее поле
(Ex,Ey).
Записывающее поле 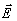 °
(
°
( ,z) распространяется в
однородной среде, и поэтому параболическое уравнение для него имеет вид:
,z) распространяется в
однородной среде, и поэтому параболическое уравнение для него имеет вид:
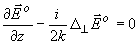 (2)
(2)
где 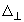 = ¶ 2/¶ x2 + ¶ 2/¶ y2.
В отличие от этого поле
= ¶ 2/¶ x2 + ¶ 2/¶ y2.
В отличие от этого поле 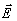 (
( ,z)
в процессе восстановления распространяется в среде, диэлектрическая проницаемость
которой промодулирована следующим образом:
,z)
в процессе восстановления распространяется в среде, диэлектрическая проницаемость
которой промодулирована следующим образом:
-
49 -
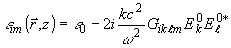 (3)
(3)
Выбор обозначения
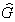 обусловлен аналогией с
работой /13/. Наиболее интересный случай оптически-изотропных регистрирующих
сред соответствует тензору
обусловлен аналогией с
работой /13/. Наиболее интересный случай оптически-изотропных регистрирующих
сред соответствует тензору 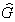 вида
вида
Gikℓm
= -æd kℓd
im (4)
Случаю æ
= ±i|æ| отвечают чисто фазовые голограммы, а наличие положительной действительности
части æ (Reæ > 0) соответствует поглощению голограммы, пропорциональному
локальной засветке. Именно этот скалярный случай подробно исследован ниже в
разделах 3¸ 5. Тем не менее, общие уравнения модовой теории в этом разделе
сформулированы для случая произвольного тензора Gikℓm. Параболическое
уравнение для восстанавливающего поля 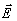 (
( ,z),
направляемого в просветной голограмме также в сторону положительных Z, имеет
вид:
,z),
направляемого в просветной голограмме также в сторону положительных Z, имеет
вид:
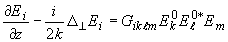 (5)
(5)
Для обсуждения
решений уравнений (2) и (5) удобно разложить поля 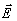 °
(
°
( ,z) и
,z) и 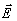 (
( ,z)
в двумерный ряд Фурье по поперечным координатам:
,z)
в двумерный ряд Фурье по поперечным координатам:
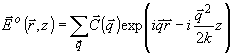 (6)
(6)
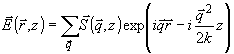 (7)
(7)
При этом
мы учли, что амплитуды  (
(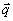 )
в силу уравнения (2) уже не зависят от Z. Следуя /4-13/, мы будем называть "модами"
голограммы такие (вообще говоря, приближенные) решения уравнения (5), для которых
выполняется соотношение:
)
в силу уравнения (2) уже не зависят от Z. Следуя /4-13/, мы будем называть "модами"
голограммы такие (вообще говоря, приближенные) решения уравнения (5), для которых
выполняется соотношение:
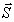 (
(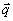 ,z)
= exp(m z)
,z)
= exp(m z) 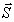 (
(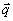 ) (8)
) (8)
Иначе говоря,будем
называть "модой" такое решение 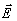 (
( ,z)
,z)
-
50 -
уравнения
(5), в котором изменение поперечной структуры как функции поперечной координаты
Z описывается решением невозмущённого волнового уравнения (2) с пространственно-однородной
диэлектрической проницаемостью e 0, а весь сложный эффект перерассеяния
на неоднородностях d e ( )
(правая часть уравнения (5)) проявляется лишь в виде простого экспоненциального
множителя ехр(m z). При этом Jmm отвечает вкладу в фазовую
скорость моды, а 2Rem - коэффициенту затухания (по интенсивности). Подстановка
выражения (6-8) в (5) и расщепление правой части (5) на ряд отдельных слагаемых
дает:
)
(правая часть уравнения (5)) проявляется лишь в виде простого экспоненциального
множителя ехр(m z). При этом Jmm отвечает вкладу в фазовую
скорость моды, а 2Rem - коэффициенту затухания (по интенсивности). Подстановка
выражения (6-8) в (5) и расщепление правой части (5) на ряд отдельных слагаемых
дает:
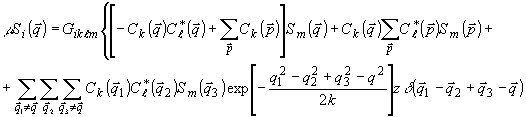 (9)
(9)
Здесь d
(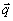 ) есть двумерный дискретный
символ Кронекера, d (
) есть двумерный дискретный
символ Кронекера, d (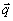 = 0) = 1, d (
= 0) = 1, d (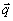 ¹
0)=1. Строго говоря, соотношение (9) не может быть точным, поскольку в правой
части (9) имеются слагаемые, явно зависящие от Z, а в левой части их нет. Однако
можно показать, что при выполнении определённых условий именно эти Z-зависящие
слагаемые в правой части (9) можно опустить (см. обсуждение аналогичного вопроса
в /6-8/ для задачи об обращении волнового фронта при вынужденном рассеянии).
Будучи переформулированным для задачи голографии одно из основных условий справедливости
такого приближения (и, вместе с ним, всей модовой теории) имеет вид:
¹
0)=1. Строго говоря, соотношение (9) не может быть точным, поскольку в правой
части (9) имеются слагаемые, явно зависящие от Z, а в левой части их нет. Однако
можно показать, что при выполнении определённых условий именно эти Z-зависящие
слагаемые в правой части (9) можно опустить (см. обсуждение аналогичного вопроса
в /6-8/ для задачи об обращении волнового фронта при вынужденном рассеянии).
Будучи переформулированным для задачи голографии одно из основных условий справедливости
такого приближения (и, вместе с ним, всей модовой теории) имеет вид:
kq
2 ³ | æ | iE° |
2 (10а)
где
q - угловая ширина записывающего излучения. Кроме того,
записывающая среда должна быть действительно объёмной, т.е.
её толщина L должна превышать длину, соответствующую угловой
расходимости пучка:
-
51 -
L
³ (kq 2)-1 (10б)
Другое
весьма существенное предположение, делаемое при отбрасывании Z-зависящих слагаемых
в (9), состоит в том, что интенсивность записывающего поля | 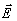 °
(
°
( )2 в среднем
(т.е. в пренебрежении отдельными интерференционными максимумами и минимумами)
постоянна по всему поперечному сечению голограммы.
)2 в среднем
(т.е. в пренебрежении отдельными интерференционными максимумами и минимумами)
постоянна по всему поперечному сечению голограммы.
Утверждение
о возможности отбросить осциллирующие вдоль по Z слагаемые в (9) можно сформулировать
ещё и в следующих терминах. Интерференция некоторых заданных Фурье-компонент
записывающего поля С (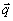 1)
и С(
1)
и С(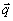 2) создаёт
в объеме голограммы периодическую решётку возмущения диэлектрической проницаемости:
2) создаёт
в объеме голограммы периодическую решётку возмущения диэлектрической проницаемости:
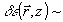 æ
æ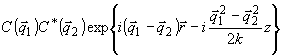 (11)
(11)
Формула
(9) описывает рассеяние восстанавливающей волны на всевозможных
решётках вида (11), причём отбрасывание Z-зависящих слагаемых
в (9) соответствует учёту только таких процессов рассеяния,
для которых точно выполнено известное условие Брэгга.
Возможность
отбросить небрэгговские слагаемые связана с их осцилляциями по Z. Кроне того,
пренебрежимо малым является вклад даже тех слагаемых в трёхкратной сумме в (9),
для которых осцилляции по Z относительно медленны (т.е. для которых (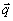 12
-
12
- 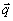 22
+
22
+ 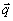 32
-
32
- 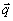 2) L/2k £
1, где L - толщина голограммы). В самом деле, в силу предположения о статистической
однородности засветки в координатном пространстве комплексные амплитуды различных
фурье-компонент С(
2) L/2k £
1, где L - толщина голограммы). В самом деле, в силу предположения о статистической
однородности засветки в координатном пространстве комплексные амплитуды различных
фурье-компонент С(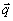 ) оказываются
независимыми. Поэтому рассеяние восстанавливающих волн на всех "чужих" решётках
(трёхкратная сумма С(
) оказываются
независимыми. Поэтому рассеяние восстанавливающих волн на всех "чужих" решётках
(трёхкратная сумма С(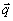 ) даёт
в среднем нуль в результате интерференции, а относительная величина отклонений
от среднего мала (см. /8/) при выполнении условий (10а). Приведённые выше рассуждения
в равной мере относятся и к сильно осциллирующим (небрэгговским) слагаемым.
) даёт
в среднем нуль в результате интерференции, а относительная величина отклонений
от среднего мала (см. /8/) при выполнении условий (10а). Приведённые выше рассуждения
в равной мере относятся и к сильно осциллирующим (небрэгговским) слагаемым.
В
таком "модовом" приближении (т.е. без Z-зависящих слагаемых)
уравнение (9) можно записать в виде:
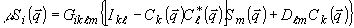 (12)
(12)
-
52 -
где
введены обозначения:
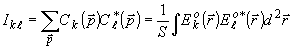 (13а)
(13а)
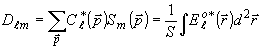 (13б)
(13б)
Эрмитова
матрица Ikℓ имеет смысл поляризованной матрицы записывающего
поля 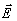 ° (
° ( ,z),
усреднённой по поперечному сечению голограммы. При этом сумма диагональных членов
J = Sр
,z),
усреднённой по поперечному сечению голограммы. При этом сумма диагональных членов
J = Sр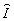 характеризует
среднюю интенсивность |
характеризует
среднюю интенсивность |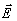 °
| 2, а структура матрицы может быть охарактеризована ещё нормированным
вектором Стокса
°
| 2, а структура матрицы может быть охарактеризована ещё нормированным
вектором Стокса  = (x
1,x 2,x 3) так, что
= (x
1,x 2,x 3) так, что
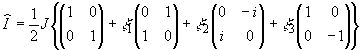 (14)
(14)
(см., например
/18/). Матрица  имеет смысл
скалярного произведения компонент поля записывающей волны и искомой моды голограммы.
Для конкретного случая "скалярной" записывающей среды (формула (4)) уравнение
(12) принимает вид:
имеет смысл
скалярного произведения компонент поля записывающей волны и искомой моды голограммы.
Для конкретного случая "скалярной" записывающей среды (формула (4)) уравнение
(12) принимает вид:
æ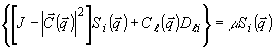 (15)
(15)
С учётом
(13б) уравнения (15) имеют вид системы уравнений для задачи на собственные значения
и собственные функции 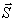 (
(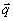 )
(моды). Из (15) следует:
)
(моды). Из (15) следует:
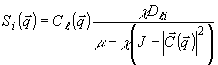 (16)
(16)
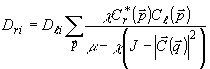 (17)
(17)
Для голографии
характерна следующая постановка задачи. Записывающее поле 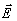 °
(
°
( ) предполагается состоящим
из двух слагаемых, первое из которых
) предполагается состоящим
из двух слагаемых, первое из которых 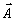 (
( ,z)
- соответствует волне, идущей от объекта, а второе
,z)
- соответствует волне, идущей от объекта, а второе 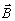 (
( ,z)
- так называемой опорной (или "референтной") волне. Соответственно, и
,z)
- так называемой опорной (или "референтной") волне. Соответственно, и  (
(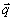 )
разбивается на
)
разбивается на
 (
(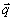 )
=
)
= 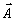 (
(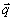 )
+
)
+ 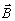 (
(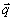 ) (18)
) (18)
-
53 -
Для объектной
волны 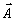 (
(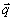 )
типичной является ситуация, когда её угловой спектр |
)
типичной является ситуация, когда её угловой спектр | 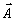 (
(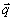 )|2
не содержит дискретных выбросов при каких-либо индивидуальных значениях
)|2
не содержит дискретных выбросов при каких-либо индивидуальных значениях 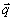 ,
так что |
,
так что |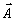 (
(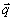 )|2
<<
)|2
<<  для каждого
для каждого 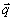 .
Что же касается углового спектра опорной волны |
.
Что же касается углового спектра опорной волны |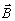 (
(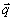 )|2,
то здесь наибольший интерес представляют два предельных случая, соответствующих
двум различным способам записи. В первом из них опорная волна также не имеет
дискретных выбросов в угловом спектре, т.е. |
)|2,
то здесь наибольший интерес представляют два предельных случая, соответствующих
двум различным способам записи. В первом из них опорная волна также не имеет
дискретных выбросов в угловом спектре, т.е. | 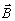 (
(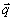 )|
2 <<
)|
2 <<  для
каждого
для
каждого 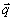 . В другой предельном
случае опорная волна состоит из двух плоских волн различных поляризаций. Наличие
именно двух плоских волн необходимо /14/ для записи информации о состоянии поляризации.
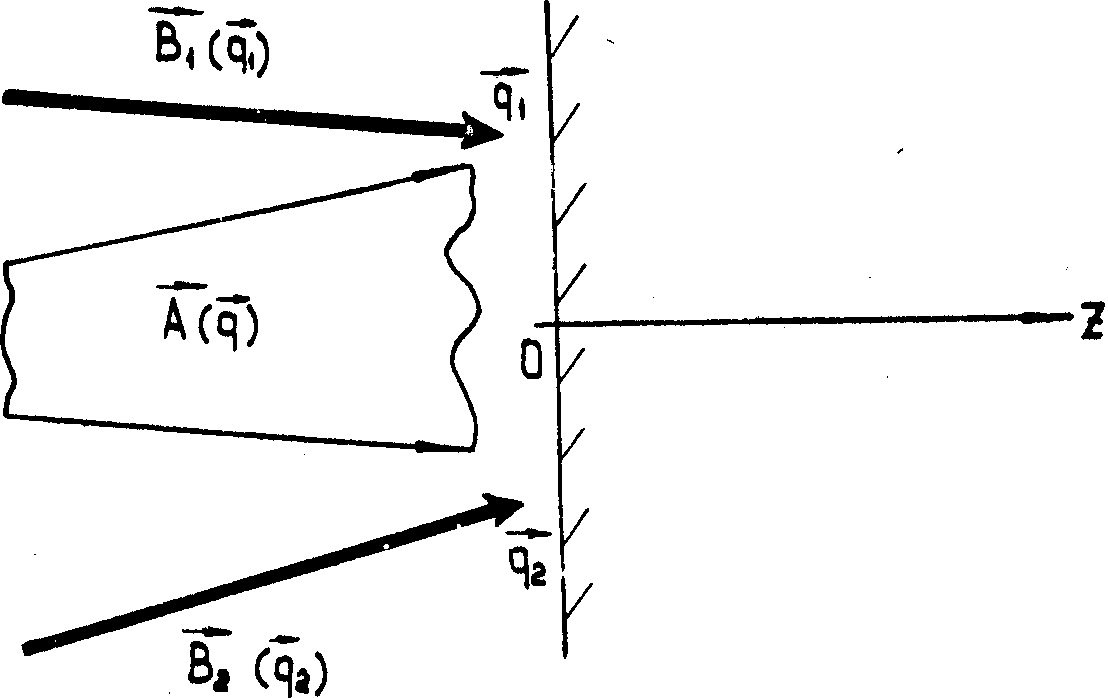
Условно два обсуждаемых способа записи изображены, соответственно, на рисунках
1а и 1б. Решению системы (16), (17) для указанных выше двух различных способов
записи посвящены, соответственно, разделы 3 и 4.
. В другой предельном
случае опорная волна состоит из двух плоских волн различных поляризаций. Наличие
именно двух плоских волн необходимо /14/ для записи информации о состоянии поляризации.
Условно два обсуждаемых способа записи изображены, соответственно, на рисунках
1а и 1б. Решению системы (16), (17) для указанных выше двух различных способов
записи посвящены, соответственно, разделы 3 и 4.
Отметин
здесь ещё одно важное свойство записывающего поля 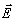 °
=
°
=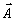 +
+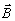 .
В некотором удалённом от голограммы сечении z = const поля
.
В некотором удалённом от голограммы сечении z = const поля 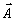 (
( ,z)
и
,z)
и 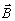 (
( ,z)
локализованы в различных участках
,z)
локализованы в различных участках  - плоскости, т.е. не перекрываются, вследствие чего можно записать равенство
- плоскости, т.е. не перекрываются, вследствие чего можно записать равенство
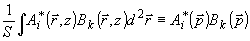 (19)
(19)
при любых
i, k. С другой стороны, как известно, скалярное произведение, т.е. интеграл
перекрытия вида (19) остаётся инвариантным в процессе распространения в силу
уравнения (2). Поэтому эти поля остаются ортогональными и в объёме записывающей
среды для любой пары компонент i, k. При атом сами компоненты полей 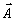 и
и 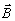 могут перекрываться как
в пространстве, так и в пространстве углов
могут перекрываться как
в пространстве, так и в пространстве углов  =
= /k,
но полный 'интеграл перекрытия (19) равен нулю. Это свойство справедливо как
для опорной волны с широким угловым спектром, так и для опорного поля, состоящего
из двух плоских волн.
/k,
но полный 'интеграл перекрытия (19) равен нулю. Это свойство справедливо как
для опорной волны с широким угловым спектром, так и для опорного поля, состоящего
из двух плоских волн.
-
54 -
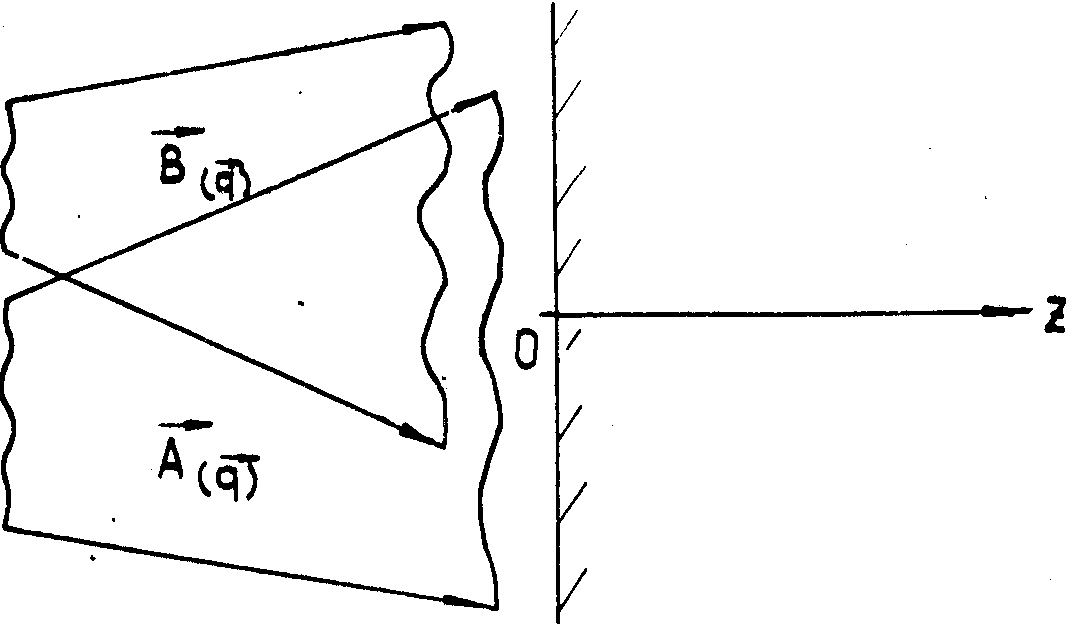
а)
Рис.1. Схема
записи голограммы опорным полем В( )
с широким угловым спектром.
)
с широким угловым спектром.
-
55 -
б)
Рис.1. Схема
записи голограммы опорным полем вида двух плоских волн ортогональных поляризаций
 1B1(
1B1( 1)+
1)+ 2B2(
2B2( 2).
В обоих случаях А(
2).
В обоих случаях А( ) - поле
объекта.
) - поле
объекта.
-
56 -
3.
Основные представления модовой теории. Моды при использовании
опорной волны с широким угловым спектром
Рассмотрим
запись голограммы опорной волны с широким угловым спектром. При этом выполняется
неравенство |  (
( )|
2 << J для любого
)|
2 << J для любого  .
Отметим, что объектная волна
.
Отметим, что объектная волна 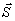 (
(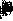 )
могла бы иметь дискретные выбросы, однако мы потребуем, чтобы их интенсивность
удовлетворяла неравенству |
)
могла бы иметь дискретные выбросы, однако мы потребуем, чтобы их интенсивность
удовлетворяла неравенству |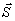 (
(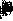 )|
2 << J, .В этом случае (т.е. при |
)|
2 << J, .В этом случае (т.е. при |  (
( )|
2 << J) уравнения (16), (17) заметно упрощаются:
)|
2 << J) уравнения (16), (17) заметно упрощаются:
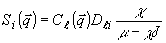 (20a)
(20a)
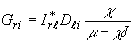 (20б)
(20б)
Наполним
свойства решения этой системы в скалярной модовой теории /4-13/. Для этого достаточно
считать матрицы 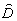 и
и 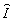 просто числами и опустить поляризационный индекс у Si и Cj.
При этом собственные функции системы (20) разбиваются на два класса. В первый
класс попадает все множество функций Е'(
просто числами и опустить поляризационный индекс у Si и Cj.
При этом собственные функции системы (20) разбиваются на два класса. В первый
класс попадает все множество функций Е'( ),
ортогональных к записывающему полю Е° (
),
ортогональных к записывающему полю Е° ( ),
и для всех таких полей собственное значение постоянной распространения и будет
одним и тем же:
),
и для всех таких полей собственное значение постоянной распространения и будет
одним и тем же:
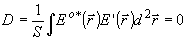 , m
= -æJ (21)
, m
= -æJ (21)
Другой
класс состоит из единственной функции, тождественно совпадающей
в данном случае с записывающим полем:
E"( )
= E° (
)
= E° ( ), m
= -2æJ (22)
), m
= -2æJ (22)
-
57 -
Поясним
смысл собственных значений m из (21), (22), следуя представлениям, развитым
в /8-11,13/ для задачи обращения волнового фронта. Из уравнений (3) и (8) при
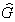 из (4) можно получить,
что для заданной собственной функции Е(
из (4) можно получить,
что для заданной собственной функции Е( )
значение m равно
)
значение m равно
m = -æ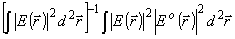 (23)
(23)
Записывающее
поле предполагается у нас состоящим из большого числа плоских волн, а предположение
о пространственной однородности засветки голограммы соответствует статистической
независимости амплитуд и фаз этих плоских волн. В силу известной центральной
предельной теоремы теории вероятностей (см., например /19/) при этом поле Е°
( ) по своей статистике является
гауссовской случайной функцией. Поля Е'(
) по своей статистике является
гауссовской случайной функцией. Поля Е'( )
из класса ортогональных к Е°(
)
из класса ортогональных к Е°( )
являются в среднем статистически независимыми от Е°(
)
являются в среднем статистически независимыми от Е°( ),
а поэтому под знаком интеграла перекрытия в (23) величины |E'(
),
а поэтому под знаком интеграла перекрытия в (23) величины |E'( )|
2 и | Е° (
)|
2 и | Е° ( )|
2 можно усреднять независимо. С учетом однородности засветки <|
E° (
)|
2 можно усреднять независимо. С учетом однородности засветки <|
E° ( )| 2>
= J = Const эту величину можно вынести из-под знака интеграла в (23), что и
дает m = -æJ.
)| 2>
= J = Const эту величину можно вынести из-под знака интеграла в (23), что и
дает m = -æJ.
Напротив
того, для поля Е"( ) = Е°(
) = Е°( )
имеем известное соотношение для моментов комплексной гауссовской случайной величины
<| E"(
)
имеем известное соотношение для моментов комплексной гауссовской случайной величины
<| E"( )| 2·|
E° (
)| 2·|
E° ( )| 2>=<|
E° (
)| 2>=<|
E° ( )| 4>=
2·<| E° | 2>·2, и для собственного значения
изучается m =-2æJ.
)| 4>=
2·<| E° | 2>·2, и для собственного значения
изучается m =-2æJ.
Эти результаты
можно интерпретировать еще и следующим образом. Можно сказать, что моды Е'( )
из класса ортогональных к Е°(
)
из класса ортогональных к Е°( )
"чувствуют" лишь среднюю по пространству часть засветки голограммы æJ,
тогда как мода Е"(
)
"чувствуют" лишь среднюю по пространству часть засветки голограммы æJ,
тогда как мода Е"( )=Е°
(
)=Е°
( ) существенным образом
"чувствует" локальные интерференционные неоднородности засветки æ|Е°
(
) существенным образом
"чувствует" локальные интерференционные неоднородности засветки æ|Е°
( ,z)|2. Замечательно,
что структура системы мод оказалась при этом чрезвычайно простой: имеется одна
мода, точно воспроизводящая записывающую волну Е°(
,z)|2. Замечательно,
что структура системы мод оказалась при этом чрезвычайно простой: имеется одна
мода, точно воспроизводящая записывающую волну Е°( ),
и все остальные моды, ортогональные к ней /6/.
),
и все остальные моды, ортогональные к ней /6/.
Запись
и восстановление голограммы при использовании опорной волны
с широким угловым спектром в рамках модовой теории /4/ проиллюстрированы
рисунком 2.
-
58 -
а) 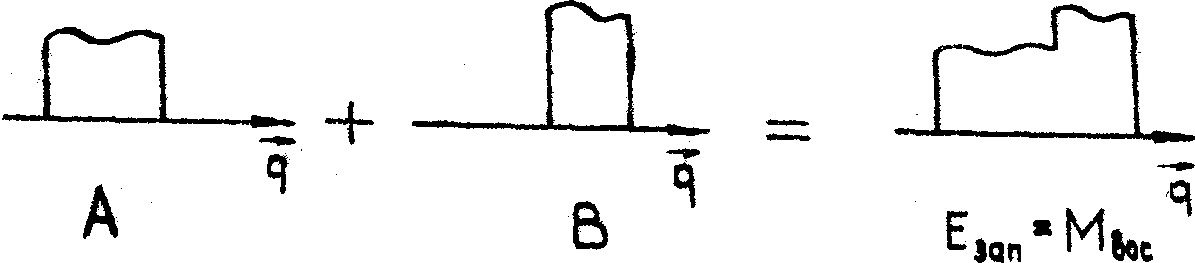
б) 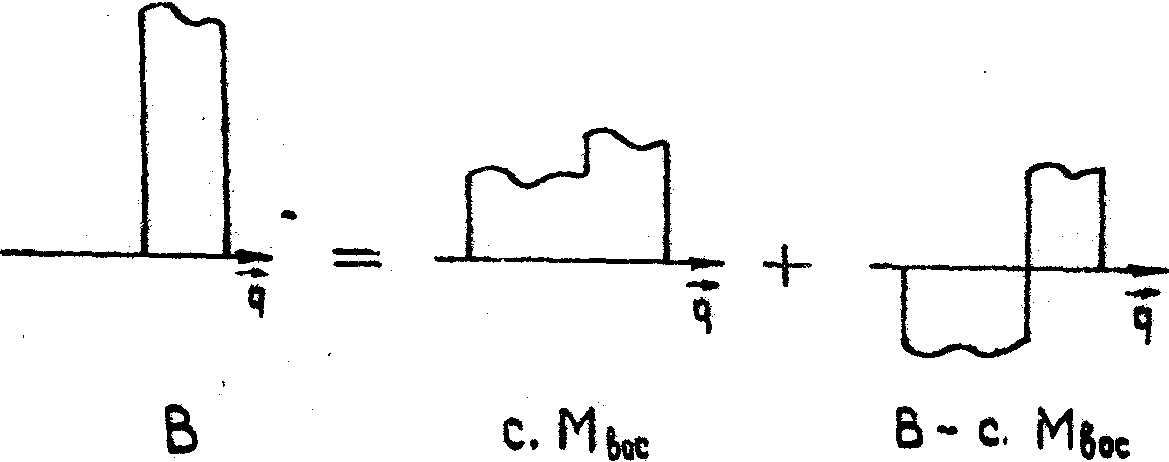
в) 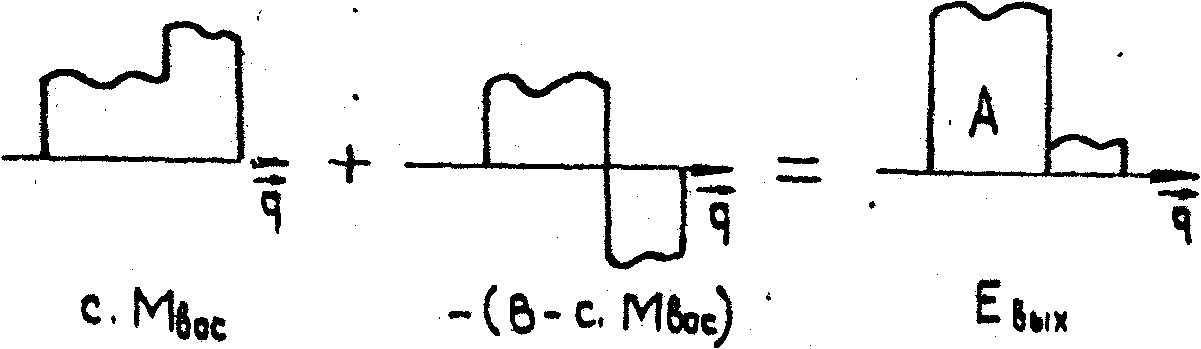
Рис.2.
Иллюстрация к кодовой теории записи и восстановления поля
объекта А при использовании опорной волны В с широким угловым
спектром. Подробности см. в тексте.
-
59 -
На
рис. 2а схематически изображены поле объекта (А) и поле
опорной волны (В), которые в сумме составляют записывающее
поле, совпадающее здесь с "воспроизводящей" модой. На рис.2б
изображено поле опорной волны В на входе в голограмму. В
терминах модовой теории это поле проектируется на "воспроизводящую"
моду и ортогональные к ней моды, соответствующее разложение
показано на рис.2б. В процессе распространения по голограмме
эти компоненты разложения приобретают экспоненциальные множители:
exp(-2æJz) для "воспроизводящей" моды и exp(-æJz)
для остальных мод. На длине Z ~ |æJ| -1
эти множители становятся существенно различными, вплоть
до знака, что условно изображено на рис.2в. В результате
сложения таких полей на выходе голограммы получается (см.рис.2в)
поле объекта А, в общем случае с высокой дифракционной эффективностью.
Конкретное выражение для дифракционной эффективности произвольных
амплитудно-фазовых голограмм получено в части II, формула
(52).
Возвращаясь
к уравнению (20).удобно в качестве базиса в пространстве индексов поляризации
взять взаимно ортогональные единичные векторы  1
и
1
и 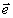 2, в которых
поляризационная матрица 1 записывающего поля диагональна:
2, в которых
поляризационная матрица 1 записывающего поля диагональна:
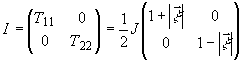 (24)
(24)
Эти орты
в общем случае соответствуют, как известно /18/, двум эллиптическим поляризациям,
ортогональным друг к другу. Орт поляризации 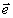 1
соответствует полностью поляризованной волне с вектором Стокса
1
соответствует полностью поляризованной волне с вектором Стокса  1
= -|
1
= -|  | , где
| , где  - вектор Стокса записывающего поля, а для орта
- вектор Стокса записывающего поля, а для орта 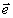 2
будет то же с
2
будет то же с  2
= -
2
= - /|
/|  |
.
|
.
Общий
вид ортов в Х и У - компонентах таков:
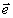 1
=
1
= 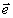 xCosD +
xCosD +
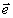 uexp[iS]SinD
,
uexp[iS]SinD
, 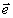 1 =
1 = 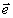 хSinD
-
хSinD
- 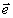 yexp[iS]CosD
(24а)
yexp[iS]CosD
(24а)
где параметры
d и D связаны с вектором Стокса  довольно сложными соотношениями (см., /18/). Частный случай линейно-
довольно сложными соотношениями (см., /18/). Частный случай линейно-
-
60 -
поляризованного
излучения (x = 0) соответствует вещественным ортам, т.е. S = 0, Случай
циркулярной поляризации (x 1 = x 3 = 0) соответствует
d = p /2, D = p /4. В этих ортах записывающее поле 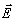 °
(
°
( ,z) может быть представлено
в виде
,z) может быть представлено
в виде
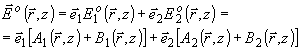 (25)
(25)
и в силу
(13а) функции Е° 1( )
и Е° 2(
)
и Е° 2( )
взаимно ортогональны.
)
взаимно ортогональны.
Решение
уравнений (20) в указанных ортах оказывается до -статочно простым и приводит
к появлению четырех (ср. с /13/) соответственных функций, компоненты которых
"воспроизводят" компоненты записывающего поля 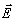 °.
Первые две функции имеют вид:
°.
Первые две функции имеют вид:
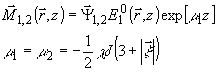 (26)
(26)
и отвечают
двукратно вырожденному собственному значению. При этом векторы 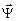 1,2
являются произвольными, но постоянными по всему объему голограммы; их удобно
считать ортогональными друг к другу. Таким образом, эти моды воспроизводят пространственную
структуру компоненты
1,2
являются произвольными, но постоянными по всему объему голограммы; их удобно
считать ортогональными друг к другу. Таким образом, эти моды воспроизводят пространственную
структуру компоненты 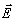 °
1(
°
1( ,z) из записывающего
поля (т.е. более интенсивной компоненты, поскольку в указанных ортах I11
= J(1+|
,z) из записывающего
поля (т.е. более интенсивной компоненты, поскольку в указанных ортах I11
= J(1+|  | )/2
I22 = J(1-|
| )/2
I22 = J(1-|  |
)/2. Сами моды отвечают полностью поляризованным полям, однако конкретная поляризация
не определена заранее, что проявляется в виде двукратного вырождения. Выражение,
для m 1, можно переписать в виде m 1 = -æ(2I11
+ I22), из которого становится особенно ясным смысл найденного решения.
Моды
|
)/2. Сами моды отвечают полностью поляризованным полям, однако конкретная поляризация
не определена заранее, что проявляется в виде двукратного вырождения. Выражение,
для m 1, можно переписать в виде m 1 = -æ(2I11
+ I22), из которого становится особенно ясным смысл найденного решения.
Моды 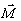 1,2 воспроизводят
E° 1 - компоненту записывающего поля. Поэтому интенсивность
I11 этой компоненты входит в выражение для с упомянутой выше "гауссовской
двойкой", а интенсивность ортогональной компоненты поля E° 2
воспринимается этой модой лишь через среднее по пространству значение I22.
1,2 воспроизводят
E° 1 - компоненту записывающего поля. Поэтому интенсивность
I11 этой компоненты входит в выражение для с упомянутой выше "гауссовской
двойкой", а интенсивность ортогональной компоненты поля E° 2
воспринимается этой модой лишь через среднее по пространству значение I22.
Аналогично
этому, вторая пара мод по своей пространственной структуре воспроизводит более
слабую компоненту Е° 2( )
записывающего поля, оставаясь вырожденной по поляризациям:
)
записывающего поля, оставаясь вырожденной по поляризациям:
-
61 -
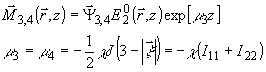 (27)
(27)
Кроме четырех
"воспроизводящих" мод, имеется класс мод, пространственная структура которых
ортогональна к функциям Е°1( )
и Е° 2(
)
и Е° 2( ).
Все эти моды имеют одно и то же собственное значение m 0 = -æJ
= -æ(I11+I22) и дополнительно двукратно вырождены
по состояниям поляризации. Зависимость собственных значений m i
от степени поляризации полного записывающего поля |
).
Все эти моды имеют одно и то же собственное значение m 0 = -æJ
= -æ(I11+I22) и дополнительно двукратно вырождены
по состояниям поляризации. Зависимость собственных значений m i
от степени поляризации полного записывающего поля |  |
при постоянной полной интенсивности J приведена на рис.3.
|
при постоянной полной интенсивности J приведена на рис.3.
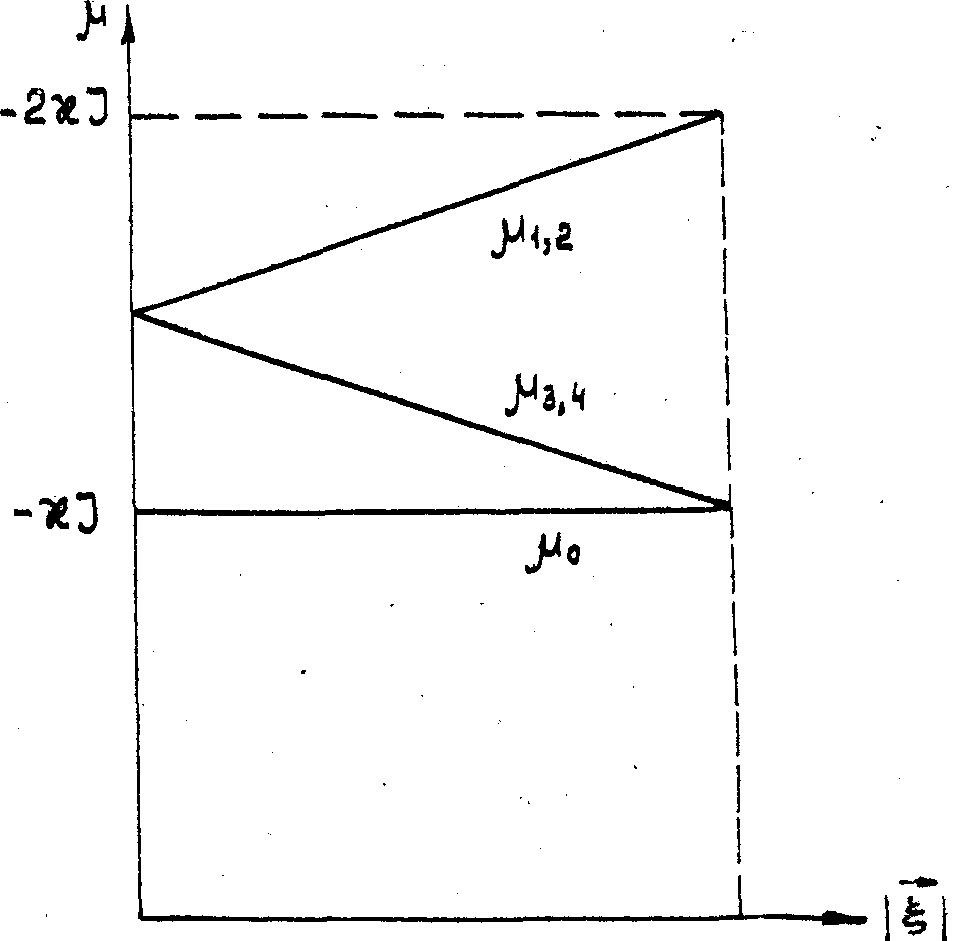
Рис.3. Зависимость
постоянных распространения m i различных мод голограммы в единицах
æJ от степени поляризации | |
записывающего поля (случай опорной волны с широким угловым спектром).
|
записывающего поля (случай опорной волны с широким угловым спектром).
-
62 -
Отметим,
что в задаче об обращении волнового фронта |13| также имеется 4 "воспроизводящих"
моды, однако они уже не вырождены по поляризациям. Вырождение в задаче голографии
обусловлено специфическим видом тензора 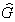 из (4), благодаря которому эффект засветки проявляется в вариациях только скалярной
части диэлектрической проницаемости среды. В задаче же вынужденного рассеяния
света тензор
из (4), благодаря которому эффект засветки проявляется в вариациях только скалярной
части диэлектрической проницаемости среды. В задаче же вынужденного рассеяния
света тензор 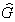 даже при рассеянии
скалярного типа имеет вид Gikℓm = constd ikd
ℓm, в результате чего свойства среды по отношений к рассеянной волне
становятся существенно анизотропными. При этом даже "ортогональные" моды теряют
поляризационное вырождение.
даже при рассеянии
скалярного типа имеет вид Gikℓm = constd ikd
ℓm, в результате чего свойства среды по отношений к рассеянной волне
становятся существенно анизотропными. При этом даже "ортогональные" моды теряют
поляризационное вырождение.
Совокупность
всех указанных выше мод образует полную систему векторных полей,зависящих от
поперечной координаты 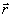 .
Значение этих мод и соответствующих собственных значений позволяет решать задачу
о распространении волны в процессе восстановления голограммы простым разложение
входного поля по системе собственных функций; эта программа будет проведена
в части II настоящей работы.
.
Значение этих мод и соответствующих собственных значений позволяет решать задачу
о распространении волны в процессе восстановления голограммы простым разложение
входного поля по системе собственных функций; эта программа будет проведена
в части II настоящей работы.
4.
Основные представления скалярной модовой теории при записи
с плоской опорной волной. Моды голограмм для случая двух
плоских опорных волн ортогональных поляризаций
В этом
разделе мы рассмотрим запись голограммы опорной волной, состоящей из двух плоских
волн ортогональных поляризаций (рис.1б). Благодаря ортогональности поляризаций
сами по себе эти две волны не создают интерференционного слагаемого в изменении
диэлектрической проницаемости голограммы. Расчет мод мы проведем для наиболее
интересного случая, когда орты 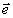 1
и
1
и 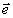 2 опорных волн
совпадают с собственными ортами поляризационной матрицы
2 опорных волн
совпадают с собственными ортами поляризационной матрицы 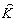 объектной волны:
объектной волны:
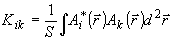 (28)
(28)
-
63 -
При этом
записывающее поле 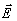 °
(
°
(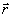 ) имеет вид:
) имеет вид:
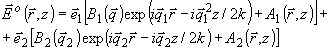 (29)
(29)
и в силу
условия диагональности матрицы 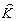 функции A1(
функции A1( ,z)
и A2(
,z)
и A2( ,z) ортогональны
друг к другу в смысле интегрирования по поперечному сечению. Именно такой выбор
поляризаций опорных волн позволяет наиболее точно восстановить поляризационную
структуру поля объекта.
,z) ортогональны
друг к другу в смысле интегрирования по поперечному сечению. Именно такой выбор
поляризаций опорных волн позволяет наиболее точно восстановить поляризационную
структуру поля объекта.
Средняя
интенсивность записывающего поля J определяется теперь так:
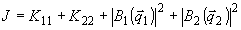 (30)
(30)
В основных
уравнениях модовой теории (16), (17) в знаменателе фигурирует разность J-| (
(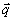 )|
2. В случае опорной волны с широким угловым спектром можно было пренебречь
величиной | C(
)|
2. В случае опорной волны с широким угловым спектром можно было пренебречь
величиной | C(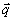 )|
2 по сравнению с полной интенсивностью J для любого
)|
2 по сравнению с полной интенсивностью J для любого 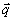 .
Теперь же это можно делать лишь для значений
.
Теперь же это можно делать лишь для значений 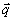 ¹
¹ 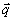 1,
1, 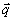 ¹
¹ 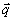 2. Напротив
того, для значений поперечного волнового вектора
2. Напротив
того, для значений поперечного волнового вектора 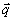 =
= 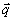 1 и
1 и 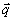 =
= 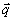 2, характеризующих
направление волн, эта разность перейдёт в J-|B1(
2, характеризующих
направление волн, эта разность перейдёт в J-|B1(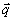 )|
2 и J-| B2(
)|
2 и J-| B2(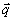 )|
2. При этой система (17) перейдёт в
)|
2. При этой система (17) перейдёт в
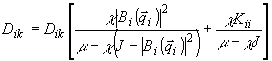 (31)
(31)
Прежде
чем обсуждать решения уравнения (36), напомним свойства
мод в скалярной задаче с одной сильной плоской волной в
записывающем поле /4,10,12/ так и в случае без сильной плоской
волны, здесь имеется подпространство "невоспроизводящих"
мод, ортогональных как к предметной, так и к плоской опорной
волне. Соответствующее собственное значение m = -æJ
определяется полной интенсивностью J. Кроне того, возникают
теперь уже две "воспроизводящие" моды. В этих модах опорная
и объектная волны воспроизводятся, но, в общей, с разными
весовыми
-
64 -
коэффициентами,
что можно записать в виде M(± ) = В+g
(± )А. При этом собственные значения равны
m (± ) = -æJr (±
), где r (+) > 1 для той моды,
в которой знаки весовых коэффициентов одинаковы g (+)
> 0 и r (-) < 1 и для моды с разными
знаками весовых коэффициентов g (-) <
0. Это связано с тем, что поле моды M(+) с g
(+) > 0 имеет максимумы за счёт интерференции
полей В и g (+). А в тех же местах голограммы,
где расположены максимумы записывающего поля, | А +
В| ; поэтому такая мода сильнее взаимодействует с наведёнными
возмущениями диэлектрической проницаемости. Для другой "воспроизводящей"
моды М(-) эффект имеет противоположный знак.
Запись
и восстановление голограммы при использовании плоской опорной
волны в рамках подовой теории /4/ проиллюстрированы рисунком
4. На рис.4а изображены полное записывающее поле, состоящее
из плоской опорной волны В и волны объекта А, а так же "воспроизводящие"
моды М(+) и М(-). В процессе восстановления
на вход голограмм подаётся плоская опорная волна В (рис.4б).
Существенно, что такая волна возбуждает в голограмме только
две "воспроизводящие" моды М(+) и М(-)
и не возбуждает ортогональных мод, это проиллюстрировано
на рис.4б. Распространение этих мод по голограмме придаёт
тли. экспоненциальные множители ехр(-æJr (±
)z), различные для мод М(+) и М(-),
вплоть до смены относительно знака, см. рис.4в. Сложение
получившихся полей на выходе голограммы даёт восстановленное
поле объекта, в общем случае с высокой дифракционной эффективностью
(см., формулу (52) из части II).
С
учётом векторного характера электромагнитных вола и скалярности
возмущений диэлектрической проницаемости вое моды голограммы,
как "воспроизводящие", так и "невоспроизводящие", являются
двукратно вырожденными по поляризациям. В этом отношении
ситуация здесь ничем не отличается от случая голографии
с широкий угловым спектром опорного поля. Собственное значение
для всех " невоспроизводящих " мод одинаково и равно m
0=-æJ.
Обсудим
теперь "воспроизводящие" решения системы (31). Имеется четыре
собственных значения:
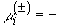 æ
æ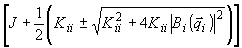 (32)
(32)
-
65 -
а) 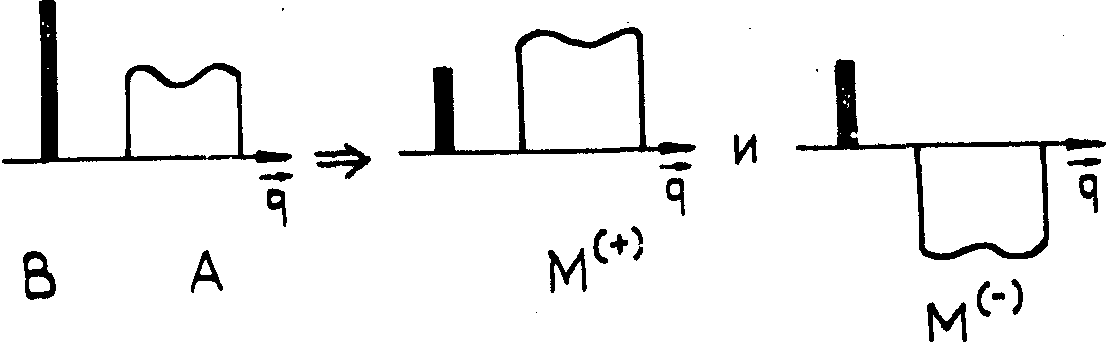
б) 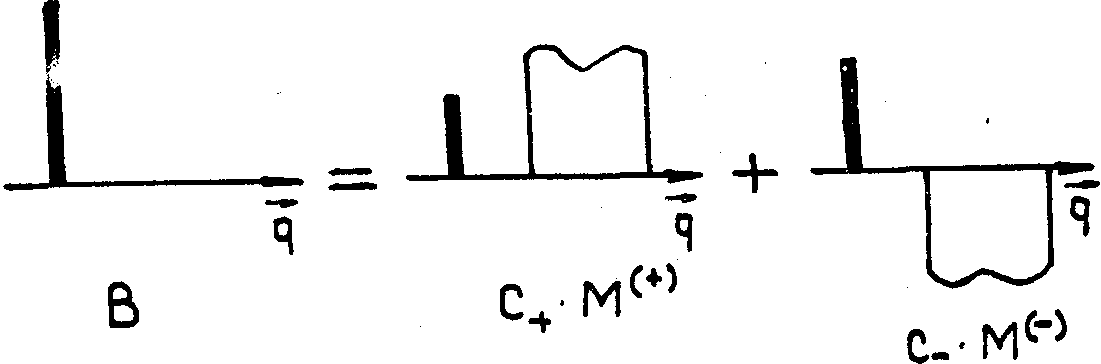
в) 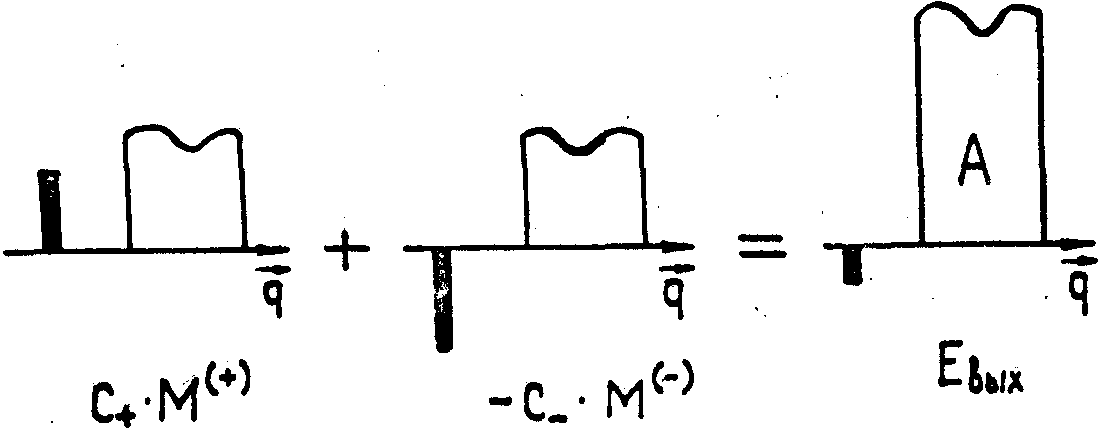
Рис.4.
Иллюстрация к модовой теорий записи и восстановления поля
объекта А при использовании опорного соля В вида плоской
волны. Подробности см. в тексте.
-
66 -
(напомним,
что суммирование по повторяющимся индексам не подразумевается).
Каждое из этих четырёх собственных значений отвечает своей
пространственной структуре моды и двукратно вырождено по
состоянию поляризации мод. Рассмотрим сначала коды с постоянными
распространениями m 1(± ).
Пространственная структура этих мод имеет вид:
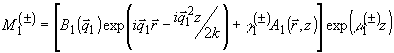 (33а)
(33а)
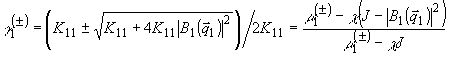 (33б)
(33б)
При этом
оказывается, что g (± )1 > 0, g (-)1
< 0. Пространственная структура мод М(± )1 имеет
такой зад, как если бы голограмма была записана полностью поляризованным полем
с единственной опорной волной 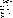 1В1
и
1В1
и 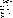 1А1
в отсутствии полей
1А1
в отсутствии полей  2А2
и
2А2
и  2В2
ортогональной поляризации. Это обстоятельство обусловлено нашим выбором в качестве
поляризаций опорных волн В1 и В2 как раз таких ортов
2В2
ортогональной поляризации. Это обстоятельство обусловлено нашим выбором в качестве
поляризаций опорных волн В1 и В2 как раз таких ортов  1
и
1
и  2, в которых
поляризационная матрица
2, в которых
поляризационная матрица  объектного поля А1 диагоиальна, вследствие чего функции A1(
объектного поля А1 диагоиальна, вследствие чего функции A1( )
и А2(
)
и А2( ) оказываются
ортогональными в смысле интегрирования по поперечному сечению голограммы. Благодаря
такой ортогональности вариации диэлектрической проницаемости d e ~
| А2 + В2| 2 влияют на распространение
мод М(± )1 только через среднее по пространству значение;
в этом можно убедиться, преобразуя выражение (32). Напротив того, вариации d
e ~ | A1 + В1| 2 влияют на моды
М(± )1 гак же, как это было бы в чисто скалярной
задаче.
) оказываются
ортогональными в смысле интегрирования по поперечному сечению голограммы. Благодаря
такой ортогональности вариации диэлектрической проницаемости d e ~
| А2 + В2| 2 влияют на распространение
мод М(± )1 только через среднее по пространству значение;
в этом можно убедиться, преобразуя выражение (32). Напротив того, вариации d
e ~ | A1 + В1| 2 влияют на моды
М(± )1 гак же, как это было бы в чисто скалярной
задаче.
На рис.5
приведены зависимости постоянных распространения m (± )1
из (32) и коэффициентов g (± )1 из (33а) от
параметра L = К11[| B1( 1)|2
+ К11]-1, т.е. от доли энергии, приходящейся на волну
объекта в полном поле с поляризацией
1)|2
+ К11]-1, т.е. от доли энергии, приходящейся на волну
объекта в полном поле с поляризацией  1.
Предельная форма таких мод при L ® 1 и при L ® 0 подробно
обсуждена в /10/ в связи с задачей обращения волнового фронта при вынужденном
рассеянии света.
1.
Предельная форма таких мод при L ® 1 и при L ® 0 подробно
обсуждена в /10/ в связи с задачей обращения волнового фронта при вынужденном
рассеянии света.
-
67 -
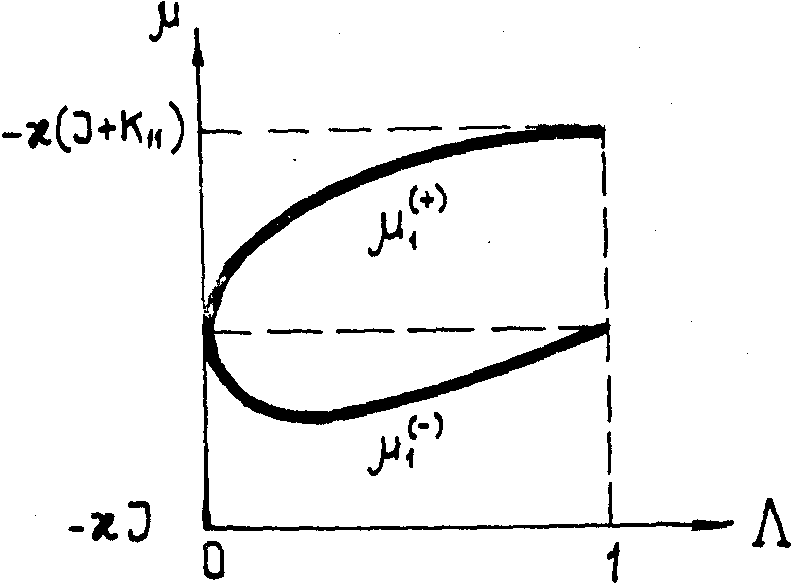
а)
Рис.5. Зависимость
постоянных распространения m (± )1 единицах
æJ для мод М(± )1 от параметра L = К11[|
В1( 1)|
+ K11]-1, характеризующего долю энергии объектной волны
в полном поле с поляризацией
1)|
+ K11]-1, характеризующего долю энергии объектной волны
в полном поле с поляризацией  1.
1.
-
68 -
б)
Рис.5.
Зависимость относительных весов g (± )1
объектной волны в модах М(± )1
от того же параметра L .
-
69 -
Совершенно
аналогичные рассуждения можно привести для мод с пространственной
структурой М(± )2, согласованной
с волнами и В2. Выражения (33) справедливы и
для этих мод, с простой заменой индекса 1 на 2.
Общая структура
мод с учётом поляризаций иллюстрируется рисунком 6; при этом каждая из четырёх
пространственных конфигураций М(± )1, М(-)1,
M(+)2 соответствует двум вырожденным поляризациям 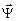 1,
1,
 2, так что полное
число воспроизводящих мод равно восьми.
2, так что полное
число воспроизводящих мод равно восьми.
Отметим
здесь следующее обстоятельство. Мы рассматриваем голограммы "просветного" типа.
Это означает, что при записи оба поля  и
и  подаются на голограмму
с одной стороны, т.е. эти волны обе распространяются в положительном направлении
оси Z. Обычно при восстановлении опорная волна также распространяется в сторону
положительных Z. Именно для такого случая были записаны основные уравнения (2)
и (5). Если же освещать голограммы при восстановлении с противоположной стороны,
то встанет вопрос о решении уравнения (5) с измененным знаком при производной
(¶ /¶ z). Мы хотим отметить здесь, что для "скалярной" записывающей
среды (т.е. удовлетворяющей условию (4)) все моды (-Z) - задачи получаются из
мод прямой задачи простым комплексным сопряжением. Напомним, что именно такое
комплексное сопряжение играет основную роль в осуществлении обращения волнового
фронта при вынужденном рассеянии света назад (см., /5/).
подаются на голограмму
с одной стороны, т.е. эти волны обе распространяются в положительном направлении
оси Z. Обычно при восстановлении опорная волна также распространяется в сторону
положительных Z. Именно для такого случая были записаны основные уравнения (2)
и (5). Если же освещать голограммы при восстановлении с противоположной стороны,
то встанет вопрос о решении уравнения (5) с измененным знаком при производной
(¶ /¶ z). Мы хотим отметить здесь, что для "скалярной" записывающей
среды (т.е. удовлетворяющей условию (4)) все моды (-Z) - задачи получаются из
мод прямой задачи простым комплексным сопряжением. Напомним, что именно такое
комплексное сопряжение играет основную роль в осуществлении обращения волнового
фронта при вынужденном рассеянии света назад (см., /5/).
Таким
образом, мы рассмотрели структуру мод общей векторной задачи
и проиллюстрировали основные положения модовой теории на
примере полностью поляризованного излучения. В части II
эти результаты будут применены для описания процесса восстановления
векторных полей. Список литературы является общим для частей
I и II, он приведён в конце части II.
-
70 -
а) 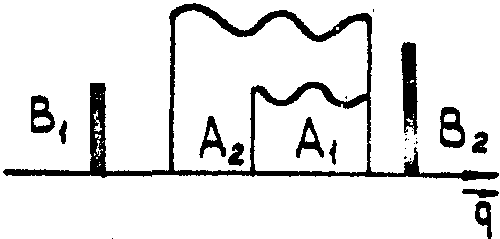
б) 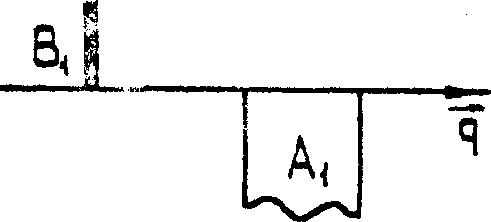 М(-)1
М(-)1
в) 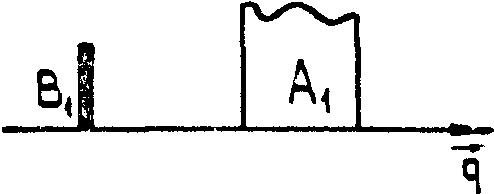 М(+)1
М(+)1
г) 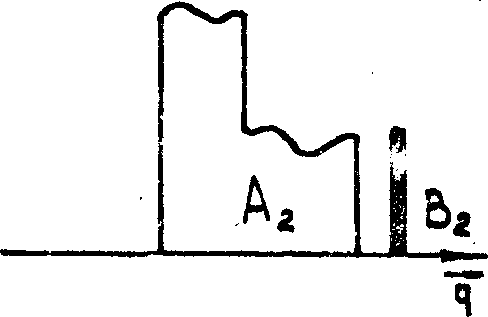 М(+)2
М(+)2
д) 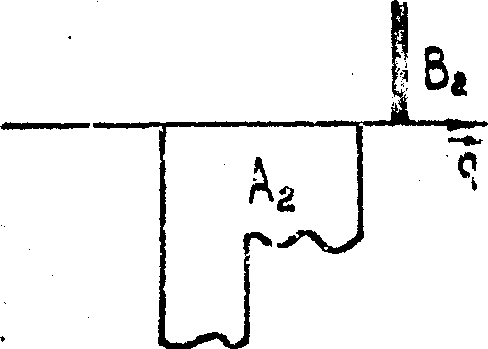 М(-)2
М(-)2
Рис.6. Структура
записывающего поля C(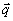 ) состоящего
из двух плоских волн
) состоящего
из двух плоских волн 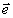 1В1
и
1В1
и 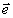 2В2
ортогональных поляризаций и опорной волны
2В2
ортогональных поляризаций и опорной волны 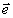 1А1
+
1А1
+ 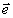 2А2.
Показана также структура мод М(+)1, М(-)1,
М(-)2, М(+)2.
2А2.
Показана также структура мод М(+)1, М(-)1,
М(-)2, М(+)2.
-
71 -
II.
ВОССТАНОВЛЕНИЕ ВЕКТОРНОГО ПОЛЯ И ПОЛЯРИЗАЦИОННЫЕ ШУМЫ
В
этой части найденная выше структура мод используется для
решения задачи о восстановлении голограммой векторного поля
объекта для обоих наиболее интересных типов опорных волн.
Для удобства ссылок нумерация формул ч.II продолжает нумерацию
формул из ч.I; то же относится ко всем обозначениям.
1.
Процесс восстановления опорной волной с широким угловым
спектром
Предположим,
что в процессе восстановления на вход голограммы подано
поле вида
Е( ,z
= 0) = a 1
,z
= 0) = a 1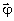 1В1(
1В1( ,z
= 0) + a 2
,z
= 0) + a 2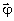 2В2(
2В2( ,z) (34)
,z) (34)
Пространственная
зависимость компонент этого поля совпадает с пространственной зависимостью компонент
опорной волны 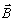 (
(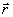 ),
использовавшейся при записи. При этом, однако, направления единичных ортогональных
векторов поляризации
),
использовавшейся при записи. При этом, однако, направления единичных ортогональных
векторов поляризации 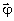 ,
, 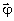 являются произвольными и не обязаны совпадать с ортами
являются произвольными и не обязаны совпадать с ортами 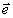 1
и
1
и 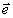 2 при записи;
к тому же допускаем, что волны
2 при записи;
к тому же допускаем, что волны 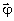 1В1
и
1В1
и 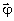 2В2
подаются на вход голограммы в общем случае с различными комплексными весовыми
множителями a 1 и a 2. Для описания восстановления
волной (34) в качестве направлений поляризации мод голограммы (26), (27) удобно
выбрать
2В2
подаются на вход голограммы в общем случае с различными комплексными весовыми
множителями a 1 и a 2. Для описания восстановления
волной (34) в качестве направлений поляризации мод голограммы (26), (27) удобно
выбрать 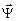 1 =
1 = 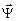 3
=
3
= 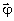 1
1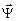 2
=
2
= 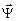 4 =
4 = 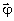 2,
а. также использовать эти орты для классификации "невоспроизводящих" мод.
2,
а. также использовать эти орты для классификации "невоспроизводящих" мод.
С учетом
сказанного решение 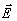 (
(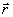 ,z)
уравнения (5) для распространения восстанавливающего поля в объеме голограммы
,z)
уравнения (5) для распространения восстанавливающего поля в объеме голограммы
-
72 -
при
начальном условии (34) имеет вид:
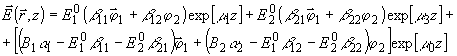 (35)
(35)
 (36)
(36)
В формуле
(35) символы Е° iBi обозначают функции Е° i(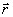 ,z)
и Вi(
,z)
и Вi(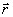 ,z), являющиеся
решениями волнового уравнения (2) для задачи распространения в неэкспонированной
голограмме. В формуле (36) из последующих выражениях суммирование но повторяющимся
индексам не подразумевается. Коэффициенты b ik имеют смысл комплексных
амплитуд проекции входного поля (34) на "воспроизводящие" моды голограммы. При
переходе в (36) от первого равенства ко второму была использована ортогональность
компонент объектного (А) и опорного (В) полей - см. формулу (19). Слагаемое
в квадратных скобках к формуле (35) является проекцией входного поля над подпространство
"невоспроизводящих" мод, т.е. мод с поперечной структурой, ортогональной к обеим
функциям Е° 1(
,z), являющиеся
решениями волнового уравнения (2) для задачи распространения в неэкспонированной
голограмме. В формуле (36) из последующих выражениях суммирование но повторяющимся
индексам не подразумевается. Коэффициенты b ik имеют смысл комплексных
амплитуд проекции входного поля (34) на "воспроизводящие" моды голограммы. При
переходе в (36) от первого равенства ко второму была использована ортогональность
компонент объектного (А) и опорного (В) полей - см. формулу (19). Слагаемое
в квадратных скобках к формуле (35) является проекцией входного поля над подпространство
"невоспроизводящих" мод, т.е. мод с поперечной структурой, ортогональной к обеим
функциям Е° 1(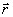 )
и Е° 2(
)
и Е° 2(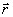 ).
Все это слагаемое описывается единой постоянной распространения m 0
=-æJ, соответствующей усредненному по объему изменению диэлектрической
проницаемости голограммы, возникшему в результате записи. С учетом равенства
(25) и формул для m k (k = 1, 3, 5) выражение (35) можно переписать
в следующем виде:
).
Все это слагаемое описывается единой постоянной распространения m 0
=-æJ, соответствующей усредненному по объему изменению диэлектрической
проницаемости голограммы, возникшему в результате записи. С учетом равенства
(25) и формул для m k (k = 1, 3, 5) выражение (35) можно переписать
в следующем виде:
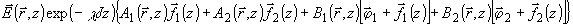 (37)
(37)
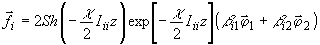 (38)
(38)
-
73 -
Формула
(37) доказывает, что рассеяние падающей опорной волны (2)
в объёме голограммы приводит к постепенному нарастанию вдоль
по Z амплитуды волны А1, А2, отображающих
структуру объекта. При этой конкретный закон нарастания
и поляризация этих волн даётся выражением (38). В частной
случае чисто фазовых голограмм æ = ± i| æ|
и ¦ (z) имеет вид осциллирующей функции ¦ i
~ Sin(| æ| Iiiz/2).
Как
уже было оказано, поля объектной (A1,А2)
и опорной (B1,B2) волн в некотором
сечении до голограммы Z < 0 пространственно разделены.
Это позволяет с помощью простых оптических систем (в частности,
с помощью глаза) разделить эти волны и после голограмм.
Тем самым, наличие слагаемых B1, В2
в прошедшем через голограмму поле не вносит искажений в
восстанавливаемом поле объекта.
Замечательно,
что никаких других волн, кроме объектной (А) и опорной (В), в голограмме не
возбуждается при освещении её полем (34). Это обстоятельство является важным
свойством объёмных голограмм и справедливо при условии применимости модовой
теории. Таким образом, в рамках скалярной теории поле объекта восстанавливается
объёмной голограммой вообще баз искажений (и без сопряженного изображения, характерного
для плоских голограмм). В отличие от этого, наличие поляризационной структуры
может приводить к появлению специфических искажений, вызываемых неоднородностью
функций передачи 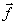 1(z)
и
1(z)
и 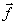 2(z). Качественная
мера этих искажений и оптимизация процессов записи и восстановления будут обсуждены
ниже в разделе 3. Формулы скалярной задачи получатся при этом как частный случай.
2(z). Качественная
мера этих искажений и оптимизация процессов записи и восстановления будут обсуждены
ниже в разделе 3. Формулы скалярной задачи получатся при этом как частный случай.
2.
Процесс восстановления опорной волной с двумя плоскими ортогонально-поляризованными
компонентами
Пусть
на экспонированную и обработанную голограмму падает восстанавливающее
поле вида:
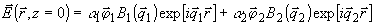 (39)
(39)
-
74 -
Можно
показать, что, как и в случае скалярной задачи, здесь поле
(39) проектируется лишь на "воспроизводящие " моды М(±
)i и не возбуждает ортогональных мод. Определяя
коэффициенты разложения по модам М(± )i
и приписывая каждой моде закон распространения exp(m
(± )iz) для поля в некотором
сечении Z голограммы найдем:
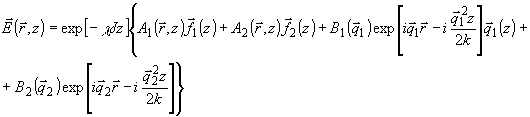 (40)
(40)
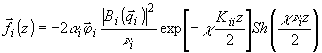 (41a)
(41a)
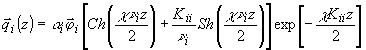 (41б)
(41б)
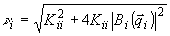 (41в)
(41в)
Как и в
случае голограммы с опорной волной, имеющей широкий угловой спектр, формы (40-41)
описывают постепенное нарастание поля объекта 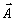 (
(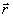 ,z)
вдоль по толщине голограммы z при подаче опорной волны
,z)
вдоль по толщине голограммы z при подаче опорной волны 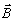 на вход голограммы Z= 0. Конкретные следствия из этих выражений для дифракционной
эффективности и для качества передачи поляризационной структуры поля объекта
приведены ниже в разделе 3.
на вход голограммы Z= 0. Конкретные следствия из этих выражений для дифракционной
эффективности и для качества передачи поляризационной структуры поля объекта
приведены ниже в разделе 3.
3.
Обсуждение поляризационных шумов и дифракционной эффективности.
Отметим,
прежде всего, что скалярный характер записанных возмущений диэлектрической проницаемости
приводит к тому, что голограмма, записанная волнами данной системы ортов поляризации
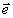 1,
1, 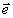 2
может быть восстановлена волнами произвольной системы ортов поляризации
2
может быть восстановлена волнами произвольной системы ортов поляризации 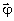 1,
1,
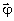 , вообще говоря, не совпадающей
с
, вообще говоря, не совпадающей
с 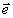 1,
1, 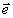 2.
На этом пути можно производить различные преобразования поляризационных свойств
излучения объекта. В настоящем разделе мы
2.
На этом пути можно производить различные преобразования поляризационных свойств
излучения объекта. В настоящем разделе мы
-
75 -
ограничимся
лишь задачей максимально точного восстановления поля объекта, включая его поляризационную
структуру. С этой целью на основе выражений (35-38) и (40-41) мы обсудим специфические
источники искажений восстановленного поля объекта,связанные с поляризацией.
При этом мы будем считать орты 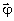 1,
1,
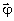 2 при восстановлении
совпадающими с ортами
2 при восстановлении
совпадающими с ортами 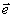 1,
1,
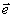 2 при записи.
2 при записи.
В силу
упоминавшейся выше разнесенности полей опорного (В) и объекта (А) в пространстве
(в некотором сечении Z) нас будут интересовать в выражениях (37) и (40) для
восстановленного поля лишь слагаемые,пропорциональные А1,2(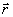 ,z),
которые для обоих способов записи имеют вид
,z),
которые для обоих способов записи имеют вид
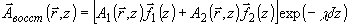 (42a)
(42a)
При
этом точное восстановление соответствовало бы полю вида
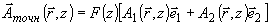 (42б)
(42б)
Перечислим
источники "поляризационных" шумов, В своей основе все они связаны с различием
поведения функций 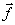 1(z)
и
1(z)
и 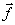 2(z) в зависимости
от Z.
2(z) в зависимости
от Z.
Прежде всего,
направления векторных функций 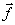 1
и
1
и  2, постоянные
вдоль по Z, могут отличаться от "идеальных" направлений
2, постоянные
вдоль по Z, могут отличаться от "идеальных" направлений  1
и
1
и  2, соответственно.
Это приводит к тому, что поле данной поляризации (например
2, соответственно.
Это приводит к тому, что поле данной поляризации (например  1)
приобретает добавку с пространственным распределением А2(
1)
приобретает добавку с пространственным распределением А2(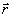 ,z),
соответствовавшим в объективной волне поляризации
,z),
соответствовавшим в объективной волне поляризации 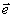 2.
Полученные нами выражения (40-41) показывают, что в схеме запаса с двумя плоскими
опорными волнами искажения такого рода отсутствуют. Это связано, однако, не
с общими свойствами такой схемы записи, а с тем обетоятельством, что орты опорных
волн при записи были выбраны совпадающими с собственными ортами поляризационной
матрицы поля объекта. Именно з этом смысле следует понимать сделанное в разделе
4 утверждение о том, что такой выбор ортов опорных воли является наилучшим.
Несовпадение направлений
2.
Полученные нами выражения (40-41) показывают, что в схеме запаса с двумя плоскими
опорными волнами искажения такого рода отсутствуют. Это связано, однако, не
с общими свойствами такой схемы записи, а с тем обетоятельством, что орты опорных
волн при записи были выбраны совпадающими с собственными ортами поляризационной
матрицы поля объекта. Именно з этом смысле следует понимать сделанное в разделе
4 утверждение о том, что такой выбор ортов опорных воли является наилучшим.
Несовпадение направлений 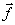 1
и
1
и 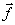 2 с направлениями
2 с направлениями
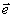 1 и
1 и 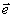 2.
В схеме записи опорной волной и широким угловым спектром обусловлено отличием
от
2.
В схеме записи опорной волной и широким угловым спектром обусловлено отличием
от
-
76 -
нуля коэффициентов
b 12 и b 21 из (36). Эти коэффициенты обращаются
в нуль в том случае, когда собственные орты поляризационных матриц объектного
и опорного полей совпадают друг с другом и, тем самым, с собственными ортами
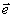 1 и
1 и 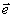 2
полного записывающего поля. Таким образом, для точного исключения искажений
такого типа необходимо, чтобы главные направления поляризационных матриц опорной
и объектной волн совпали.
2
полного записывающего поля. Таким образом, для точного исключения искажений
такого типа необходимо, чтобы главные направления поляризационных матриц опорной
и объектной волн совпали.
Другой
источник искажений состоит в различии комплексных амплитуд, соответствующих
векторам 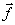 1(z)
и
1(z)
и 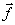 2(z). Это различие
в свою очередь удобно подразделить на сомножители, независящие и зависящие от
Z. В схеме записи с широким угловым спектром опорной волны при b 12
= b 21 = 0, восстановленное поле имеет вид (42а) с
2(z). Это различие
в свою очередь удобно подразделить на сомножители, независящие и зависящие от
Z. В схеме записи с широким угловым спектром опорной волны при b 12
= b 21 = 0, восстановленное поле имеет вид (42а) с
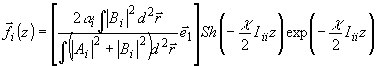 (43)
(43)
Второй сомножитель
(Z-зависящий) различен для функций 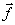 1
и
1
и 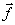 2 в меру различия
диагональных элементов I11 и I22 поляризационной матрицы
полного записывающего поля. Различие этих множителей пропадает при I11
=I22, что отвечает случаю полностью неполяризованного полного записывающего
поля. Первый сомножитель в
2 в меру различия
диагональных элементов I11 и I22 поляризационной матрицы
полного записывающего поля. Различие этих множителей пропадает при I11
=I22, что отвечает случаю полностью неполяризованного полного записывающего
поля. Первый сомножитель в 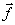 1
и
1
и 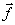 2 не зависит
от Z; его можно сделать одинаковым для
2 не зависит
от Z; его можно сделать одинаковым для 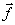 1
и
1
и 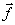 2 несколькими
способами. Рассмотрим сначала случай, когда восстанавливающая волна полностью
идентична опорной, т.е. a 1 = a 2. При этом для
совпадения независящих от Z сомножителей в (43) нужно сделать одинаковыми не
только главные направления поляризации полей А и В, но и степени поляризации
(т.е.1 только направления ,но и величины векторов Стокса
2 несколькими
способами. Рассмотрим сначала случай, когда восстанавливающая волна полностью
идентична опорной, т.е. a 1 = a 2. При этом для
совпадения независящих от Z сомножителей в (43) нужно сделать одинаковыми не
только главные направления поляризации полей А и В, но и степени поляризации
(т.е.1 только направления ,но и величины векторов Стокса  A
и
A
и  B). Кроме того,
имеется возможность делать одинаковыми комплексные амплитуды ¦ 1(z)
и ¦ 2(z), варьируя один из комплексных коэффициентов a 1
и a 2, с которыми поляризации "1" и "2" представлены в опорной
волне при восстановлении по сравнению с опорной волной при записи. Такая вариация
позволяет при заданной толщине голограммы Z добиться точного восстановления
волны объекта даже при I11 ¹ I22 и при |
B). Кроме того,
имеется возможность делать одинаковыми комплексные амплитуды ¦ 1(z)
и ¦ 2(z), варьируя один из комплексных коэффициентов a 1
и a 2, с которыми поляризации "1" и "2" представлены в опорной
волне при восстановлении по сравнению с опорной волной при записи. Такая вариация
позволяет при заданной толщине голограммы Z добиться точного восстановления
волны объекта даже при I11 ¹ I22 и при |  A|
¹ |
A|
¹ |  B|
(но при
B|
(но при  A
| |
A
| |  B).
B).
-
77 -
Для схемы
записи с плоскими опорными волнами выражения (41а), (41б) с 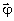 1=
1=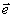 1,
1,
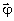 2 =
2 = 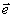 2
позволяют сделать примерно такие же выводы. Именно, Z-зависящие множители будут
идентичны только в том случае, если поле объекта полностью неполяризовано (К11
= К22; К12 = К*21 = 0), а интенсивности
двух опорных плоских волн одинаковы |В1|2 = |B2|2.
При выполнении указанных условий будут совпадать и независящие от Z сомножители
в (41а) (при a 1 = a 2). Кроме того, как и в предыдущей
схеме записи, остается возможность сделать амплитуды
2
позволяют сделать примерно такие же выводы. Именно, Z-зависящие множители будут
идентичны только в том случае, если поле объекта полностью неполяризовано (К11
= К22; К12 = К*21 = 0), а интенсивности
двух опорных плоских волн одинаковы |В1|2 = |B2|2.
При выполнении указанных условий будут совпадать и независящие от Z сомножители
в (41а) (при a 1 = a 2). Кроме того, как и в предыдущей
схеме записи, остается возможность сделать амплитуды 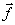 1(z)
и
1(z)
и 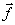 2(z) совпадающими
для данного г путем вариации одного из коэффициентов a 1 и a
2.
2(z) совпадающими
для данного г путем вариации одного из коэффициентов a 1 и a
2.
Ваше
были перечислены случаи идеального восстановления векторного
поля объекта. Отметим теперь ряд случаев, когда поле объекта
восстанавливается хотя и не идеально, но все же довольно
точно. Первый случай - голограммы с малым значением æJz,
т.е. с малой дифракционной эффективностью. В этом случае
результаты модовой теории совпадают с результатами расчетов
в первом Бориовском приближении. При этом в схеме записи
с плоскими опорными волнами
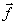 i(z)
= a iæ|
Bi| 2z
i(z)
= a iæ|
Bi| 2z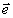 i
(44)
i
(44)
Отсюда следует,
что при d1 = d2 для восстановления в этом приближении
векторного поля объекта 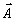 (
(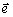 ,z)
достаточно иметь одинаковыми интенсивности двух поляризаций опорной волны. (Напомним,
что орты поляризации
,z)
достаточно иметь одинаковыми интенсивности двух поляризаций опорной волны. (Напомним,
что орты поляризации 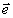 1
и
1
и 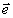 2 выбирались
как собственные орты матрицы записывающего поля). В схеме с широкоугольной опорной
волной при a 1 = a 2, в 1-ом Борковском приближении
для правильного восстановления объекта нужно потребовать
2 выбирались
как собственные орты матрицы записывающего поля). В схеме с широкоугольной опорной
волной при a 1 = a 2, в 1-ом Борковском приближении
для правильного восстановления объекта нужно потребовать
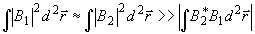 (45)
(45)
т.е.
нужно, чтобы поле опорной волны было близко к полностью
деполяризованному.
Другой случай,
на который хотелось бы обратить особое внимание, это случай, когда интенсивность
опорной волки с широким угловым спектром при записи много больше интенсивности
волны, объекта | 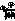 |
2 >> |
|
2 >> | |2.
При этом из полученных выше формул следует
|2.
При этом из полученных выше формул следует
-
78 -
важный
вывод; для правильной передачи векторного поля объекта достаточно,
чтобы опорная волна была полностью не поляризованной.
Для
количественной характеристики степени восстановления векторного
поля удобно ввести полную энергию UA, идущую
на выходе из голограммы в процессе восстановления в направлении
объекта:
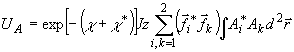 (46а)
(46а)
Введём
также долю энергии VA в проекции; речь идёт об энергии, приходящейся
в волне 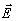 (
(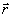 ,z)
при выходе из голограммы на ее проекцию на истинное поле объекта
,z)
при выходе из голограммы на ее проекцию на истинное поле объекта 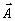 (
(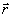 ,z):
,z):
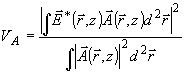 (46б)
(46б)
Тогда
относительная величина шума ответ быть определена как
Ршум
= (UA – VA)/VA (47)
В
наиболее .интересном случае, когда
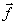 1(z)
= ¦ 1(z)
1(z)
= ¦ 1(z)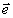 1;
1; 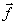 2(z)
= ¦ 2(z)
2(z)
= ¦ 2(z)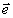 2 (48а)
2 (48а)
(см.
выше), выражение Ршум принимает вид:
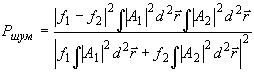 (48б)
(48б)
с
помощью которого нетрудно подсчитать относительную величину
"поляризованного" шути в каждой конкретной случае.
Формула
для поляризованных шумов, аналогичная (48б), но получаемая без предположения
(48а), также была найдена нами, однако ввиду ее громоздкости здесь она не приводится.
Приведём оценки уровня "поляризационных" шумов, связанных с появлением волн
вида А1(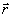 )
)
-
79 -
поляризации
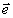 2 и, наоборот,
волн А2(
2 и, наоборот,
волн А2(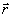 ) на
поляризации
) на
поляризации 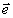 1.
Относительная величина амплитуды этих "неправильных" слагаемых может быть оценена
так:
1.
Относительная величина амплитуды этих "неправильных" слагаемых может быть оценена
так:
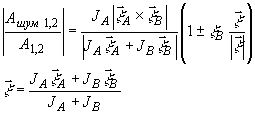 (49)
(49)
Таким образом,
и для этого типа поляризационных искажений малой их величины можно добиться
подбором условий записи. Именно, можно, например, сделать интенсивность частично
деполяризованной опорной волны иного большей, чем у волны объекта, и тогда не
нудна априорная информация о поляризованных свойствах объектной волны (о её
векторе Стокса  А).
Другой способ подавления этих искажений основан на подборе поляризационных свойств
опорной волны (её вектора Стокса
А).
Другой способ подавления этих искажений основан на подборе поляризационных свойств
опорной волны (её вектора Стокса  В),
совпадающих со свойствами поля объекта, так, чтобы
В),
совпадающих со свойствами поля объекта, так, чтобы  В
было параллельно
В
было параллельно  А.
Напомним, что поляризационные шумы, связанные с несовпадением амплитуд "правильных"
поляризаций (
А.
Напомним, что поляризационные шумы, связанные с несовпадением амплитуд "правильных"
поляризаций (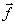 1
1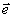 1),
(
1),
(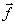 2
2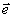 2)
могут быть (при фиксированной толщине голограммы Z) устранены вариацией коэффициентов
a 1 и a 2.
2)
могут быть (при фиксированной толщине голограммы Z) устранены вариацией коэффициентов
a 1 и a 2.
Полученные
выше выражения для восстановленного векторного поля позволяют найти дифракционную
эффективность h объёмной голограммы. Возможны два определения величины
h . В одном из них величина h = h u определяется как
отношение полной энергии UA, восстановленной в направлении объекта,
к энергии входного поля | a 1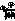 1
+ a 2
1
+ a 2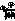 2| 2.
В другом (см. /12) h = h V определяется как дифракционная
эффективность по отношению к восстановлению точного поля объекта; энергия в
этой "точной" проекции обозначалась выше в (46б) как VА:
2| 2.
В другом (см. /12) h = h V определяется как дифракционная
эффективность по отношению к восстановлению точного поля объекта; энергия в
этой "точной" проекции обозначалась выше в (46б) как VА:
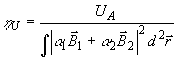 ;
; 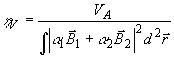 (50)
(50)
-
80 -
Для
обоих определений нахождение дифракционной эффективности
по формулам (46), (50) и выражениям для полей на выходе
(57), (38) и (40), (41) не представляет особых затруднений
и приводит к довольно громоздким, но простым выражениям.
В
случае полностью поляризованного излучения (и в рамках применимости
модовой теории) искажения могли бы быть обусловлены лишь
усадкой материала голограммы в процессе проявления или ещё
рядом причин, приводящих к так называемым "спектральным"
искажениям. Отсылая по поводу "спектральных" искажений к
теоретической работе /12/, здесь мы будем считать их отсутствующими.
Таким образом, в этих условиях переход к полностью поляризованному
излучению снимает вообще все возможные искажения. При этом
оба определения дифракционной эффективности совпадают и
дают для опорной ,волны с широким угловым спектром
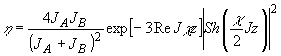 (51)
(51)
и
для плоской опорной волны
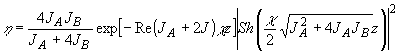 (52)
(52)
Здесь
J = JA+JB, а JA и JB
- интенсивности объектной и опорной волны, соответственно.
Формула
(52) для определённого случая чисто фазовых голограмм (æ
= ± i| æ|) была ранее получена в работе /4/.
Имея
выражения для дифракционной эффективности и поляризационных
шумов, можно решать задачу оптимизации, т.е. нахождения
компромисса между достижением высокой дифракционной эффективности,
-
81 -
с
одной стороны, и высокой точности восстановления векторного
поля, с другой.
4.
Запись и восстановление голограмм при полностью поляризованной
опорной волне.
Обсудим
специальный случай записи, наиболее распространенный на
практике. Именно, чаще всего в качестве опорной волны используется
полностью поляризованное излучение. С другой стороны, поле
объекта, как правило, является не полностью поляризованным,
поскольку разные точки объекта испускают волны разных поляризаций.
Напомним, что мы рассматриваем строго монохроматические
поля, и поэтому понятие частичной поляризованности связано
у нас не с обычным /18/ усреднением по времени, а с усреднением
по поперечному сечению голограммы.
Рассмотрим
случай полностью поляризованной опорной волны с широким угловым спектром. Это
означает, что компоненты В1( ,z)
и B2(
,z)
и B2( ,z) опорной
волны при записи (формула (25)) в разложении по собственным ортам
,z) опорной
волны при записи (формула (25)) в разложении по собственным ортам 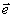 1,
1,
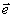 2 поляризационной
матрицы полного записывающего поля А + В пропорциональны друг другу, т.е.
2 поляризационной
матрицы полного записывающего поля А + В пропорциональны друг другу, т.е.
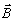 (
( ,z)
=
,z)
= 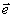 1В1(
1В1( ,z)
+
,z)
+ 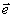 2В2(
2В2( ,z)
= (Р1
,z)
= (Р1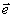 1
+ Р2
1
+ Р2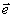 2)В(
2)В( ,z)
=
,z)
= 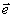 3В(
3В( ,z) (53а)
,z) (53а)
Тогда
при восстановлении обработанной голограммы волной вида
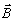 '(
'( ,z)
= (Q1
,z)
= (Q1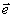 1
+ Q2
1
+ Q2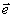 2)В(
2)В( ,z)
=
,z)
= 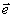 bВ(
bВ( ,z) (53б)
,z) (53б)
-
82 -
отличающийся
от поля (53а) лишь комплексный ортом поляризации, на выходе
из голограммы в направлении, соответствующем изображению
объекта, будут идти волны вида
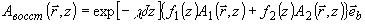 (54а)
(54а)
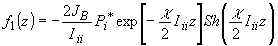 (54б)
(54б)
Особенно
простой вид эта формула принимает в условиях применимости
Борновского приближения, когда
¦
i(z) = - 2JBæzP*i (54в)
Обсудим
полученные выражения. Как и следовало ожидать, голограмма со скалярной средой
не меняет (единственного) состояния поляризации падающей на неё волны В из (53б).
Пространственная структура восстановленного поля даётся линейной комбинацией
компонент поля объекта А1( ,z)
и А2(
,z)
и А2( ,z) с комплексными
весами ¦ 1(z) и ¦ 2(z).
,z) с комплексными
весами ¦ 1(z) и ¦ 2(z).
В Борновском
приближении из (54а,в) следует, что восстановленное поле имеет пространственную
структуру проекции (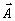 (
( ,z)·
,z)·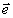 *3)
полного векторного поля объекта
*3)
полного векторного поля объекта 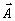 (
( ,z)
на орт
,z)
на орт 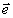 3), записывающего
опорного поля (53а). В отличие от этого, в случае высокой дифракционной эффективности
восстановленное полз имеет пространственную структуру проекции (
3), записывающего
опорного поля (53а). В отличие от этого, в случае высокой дифракционной эффективности
восстановленное полз имеет пространственную структуру проекции (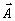 (
( ,z)·
,z)·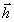 *3) того же поля
*3) того же поля 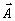 (
( ,z)
на некоторый орт
,z)
на некоторый орт 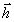 (z), вообще
говоря, зависящий от толщины голограммы:
(z), вообще
говоря, зависящий от толщины голограммы:
-
83 -
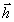 (z)
= const(
(z)
= const(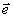 1
1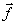 *1(z)
+
*1(z)
+ 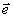 2
2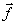 *2(z)) (56)
*2(z)) (56)
При
этом появляется принципиальная возможность восстановления
различных поляризационных компонент поля объекта при записи
полностью поляризованной опорной волной за счет вариаций
толщины голограммы.
Точные выражения
для решения аналогичной задачи с плоской опорной волной довольно громоздки.
В частности, уже для нахождения собственных значений у;. мод голограммы требуется
решать кубическое уравнение. (Напомним, что выше в разделе 4 Части I мы избежали
подобной трудности (решения уравнения 4-ой степени) за счет выбора ортов двух
опорных волн вдоль главных направлений поляризационной матрицы волны объекта)
По этой причине мы не приводим здесь точного выражения для 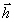 (z)
, Тем не менее сама структура выражений, свойства Борновского приближения и
остальные качественные выводы остаются теми же и для случая с плоской опорной
волной. В частности, если орт
(z)
, Тем не менее сама структура выражений, свойства Борновского приближения и
остальные качественные выводы остаются теми же и для случая с плоской опорной
волной. В частности, если орт 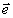 3
опорной волны при записи совпадает с одним из собственных ортов поляризационной
матрицы опорного поля, то для любых значений: толщины голограммы г восстанавливается
только компонента (
3
опорной волны при записи совпадает с одним из собственных ортов поляризационной
матрицы опорного поля, то для любых значений: толщины голограммы г восстанавливается
только компонента (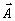 (
( ,z)·
,z)·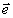 3).
3).
5.
Заключение.
Таким
образом в настоящей работе построена теория восстановления
волны объекта с учетом ее поляризации просветленными объемными
голограммами. Представляют также большой самостоятельный
интерес определенный случай получения в работе выражений,
относящийся к записи и восстановлению поляризованного излучения
общими (амплитудно-фазовыми) объемными голограммами.
-
84 -
Литература
1.
Ю.Н.Денисюк. ДАН СССР, 144 , 1275, 1962.
2.
Н.Kogelnik, Bell, Syst.Techn. J. 48, 2909 (1969).
3.
В.В.Аристов, В.Ш.Шехтман. УФН, 104, 51, 1971.
4.
В.Г.Сидорович, ЖТФ, 46, 1306, 1976.
5.
Б.Я.Зельдович, В.И.Поповичев, В.В.Рагульскйй, Ф.С.Файзуллов.
Письма в ЖЭТФ, 15, 160 , 1972.
6.
В.Г.Сидорович. ЖТФ, 46, 2168, 1976.
7.
И.М.Бельдгогин, М.Г.Галушкин, Е.М.Земсков, В.И.Мандросов.
Квантовая электроника, 3, 2467, 1976.
8.
Б.Я.Зельдович, В.В.Шкунов. Квантовая электроника, 5,
1, 1978.
9.
Б.Я.Зельдович, В.В.Шкунов. Квантовая электроника, 4,
1090, 1977.
10.
Б.Я.Зельдович, В.В.Шкунов. Квантовая электроника, 4
11, 1977.
11.
Н.Б.Баранова, Б.Я.Зельдович, В.В.Шкунов. Препринт Института
пройдем механики АН СССР №90, 1977.
12.
Б.Я.Зельдович, В.В.Шкунов. Препринт ФИАН, 1977.
13.
A.W.Lohman, Appl.Opt., 4, 1667 (1965).
14.
И.А.Дергогин, В.Н.Курашов. УФН, 108, 733, 1972.
15.
Ш.Д.Какичашвили, Оптика и спектроскопия, 42, 390,
1977.
16.
В.Н.Курашов, Д.В.Паданчук, В.Г.Черемис. Квантовая электроника,
4 (10), 2157, 1977.
17.
М.Борн, Э.Вольф. Основы оптики, М., Наука, 1973.
18.
В.Б.Давенпорт, В.Л.Рут. "Введение в теорию случайных сигналов
и шумов", М., ИЛ, 1960.

