КИНОФОРМ
- ГОЛОГРАММА – ПОЛЯРИЗАЦИЯ
Ш.Д.Какичашвили
Использован
единый теоретический подход к анализу образования изображения
киноформом и голограммой.
Рассматриваются
искажения в реконструированном киноформом изображении при
отображении на нем информации только о фазе и только об
амплитуде объектного поля. Тем самым показана необходимость
комплексной (амплитудно-фазовой) реализации киноформа. Рассматривается
n-цветный киноформ, позволяющий наряду с комплексной амплитудой
реконструировать цвет объекта.
В
изложенном контексте двухлучевая голограмма интерпретируется
как результат технологического приема отображения комплексной
амплитуды объектного поля путем его фоторегистрации. При
этом образованный таким путем "киноформ" страдает шумами
с формированием побочных изображений. Рассмотрен наиболее
общий случай амплитудно-фазовой модуляции голограммной среды
для тонкой голограммы.
Предложен
поляризационный комплексный киноформ, представляющий собой
прозрачность с поверхностно-переменной анизотропией. Подобное
устройство способно реконструировать состояние поляризации
волнового поля объекта. Анализируется векторная система
уравнений поляризационного киноформа, устанавливающая связь
между параметрами реконструируемого поля и материальными
характеристиками анизотропной среды киноформа. Обсуждается
недоступная для скалярного киноформа возможность его физической
реализации путем поляризационно-голографической съемки на
фотоанизотропных средах.
-
6 -
Киноформ
Основная
идея голографии, как известно, заключается в двухэтапном
формировании изображения. На первом этапе комплексная амплитуда
рассеянного объектом поля более или менее адекватным образом
поточечно отображается на материальном носителе - голограмме.
На втором этапе организованный таким путем материальный
носитель используется для реконструкции - повторного формирования
поля исходного объекта. При этом собственно запись в среде
не всегда имеет место. Так, процесс визуализации акустических
объектов путем дифракции света на бегущей или же стоячей
деформации раздела жидкость - воздух протекает в реальном
масштабе времени без всякой записи. Тем не менее, процесс
этот - типичный пример использования голографического метода.
С другой стороны, киноформ, фактически являющийся идеальной
голограммой, не создающей побочных изображений, как будет
показано это для скалярной теории в данной работе, не монет
быть получен путем голографической регистрации. Более того,
свет может вообще не участвовать в его физическом воплощении,
а информация об объектном поле, полученная ЭВМ, может реализоваться
на материальном носителе путем травления, гравировки и пр.
Очевидно,
что упомянутая выше двухэтапность формирования изображения
могла бы оказаться бесцельной, если бы не потребности хранения,
апостериорной обработки трехмерных изображений и появляющая
возможность наперед заданной трансформации волновых полей
во временных (двухэкспозиционная голография) и пространственных
(масштабные преобразования) интервалах. Кроме того, своеобразная
информационная равнозначность локализованного объекта и
отображенного на материальном носителе рассеянного им поля
может служить важным эвристическим принципом для ряда областей
науки (например, т.н. голографическая модель мозга используется
в нейропсихологии).
Основная
задача голографии, по крайней мере в принципе, может быть
решена чрезвычайно просто, что обусловлено гармоническим
характером когерентного волнового поля.
-
7 -
Действительно,
в данной среде мгновенное состояние волнового поля на поверхности
(например, плоскости) несет полную информацию о предыстории
и будущем сформированного объектом фронта. Смоделировав
поверхность в виде переменной прозрачности так, что непосредственно
за ней поле при просвечивании идентично исходному объектному,
мы решим задачу голографической реконструкции, опираясь
на принцип Гюйгенса-Френеля. Следует подчеркнуть, что подобная
голограмма явилась бы идеалом голографической записи, так
как при реконструкции не имело бы места формирование побочных
изображений.
Рассмотрим
случай подобного моделирования комплексной амплитуды объектного
поля на плоскости с последующей реконструкцией плоской волной.
Так как форм поверхности и форма реконструирующей волны
являются свободными параметрами, при таком рассмотрении
упрощается расчет без ограничения общности полученных результатов.
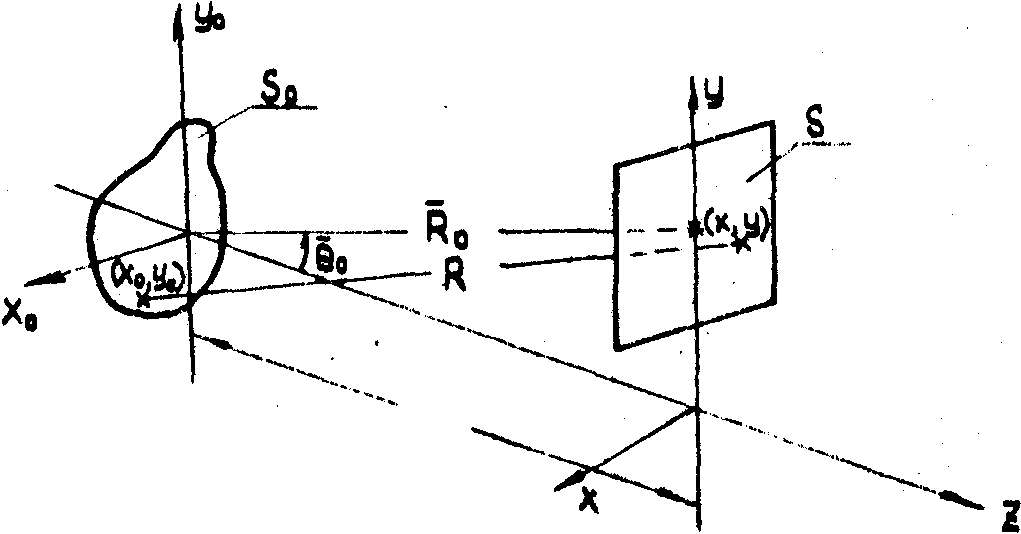
Рис.1.
-
8 -
На
рис.1, а) S0 - объект. В плоскости ХОУ, расположенной
в начале координат, проводится наблюдение. В эту же плоскость
затем помещается соответствующим образом промоделированный
материальный носитель S, формирующий идентичный объектному
фронт при просвечивании плоской волной.
Мгновенное
состояние волнового поля объекта в момент времени t0
можно записать в виде
X
(x,y,t0) = a(x,y)exp[ij (x,y)]exp(iw
t0) (1)
Наша задача
заключается в создании соответствующей (1) вариации комплексного коэффициента
преломления носителя S как функции координат 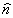 (x,у)=n(х,у)[1-it
(x,у)], где n(x,y) - коэффициент преломления, a t (x,y) - коэффициент экстннкции
.
(x,у)=n(х,у)[1-it
(x,у)], где n(x,y) - коэффициент преломления, a t (x,y) - коэффициент экстннкции
.
После
просвечивания S плоской монохроматической волной частоты
w ' поле за прозрачностью опишется выражением:
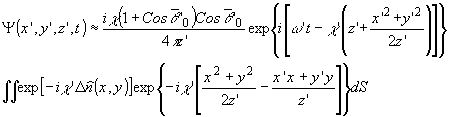 (2)
(2)
где D
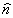 (х,у) =
(х,у) = 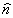 (х,у)
-
(х,у)
- 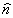 0(x,y) (
0(x,y) (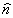 0(х,у)
исходный комплексный коэффициент преломления среды в немодулированном состоянии,
0(х,у)
исходный комплексный коэффициент преломления среды в немодулированном состоянии,
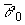 - средний угол наблюдения.
- средний угол наблюдения.
Примем
линейный закон соответствия характеристик волнового поля
и материальной среды:
|
exp(-æ'nt
) = ka(x,y)
|
(3)
|
|
exp(-iæ'n)
= exp{i[j (x,y) + e ]}
|
|
-
9 -
где
k и e - произвольные постоянные.
Выражая
амплитуду и фазу рассеянного объектом поля через дифракционный
интеграл:
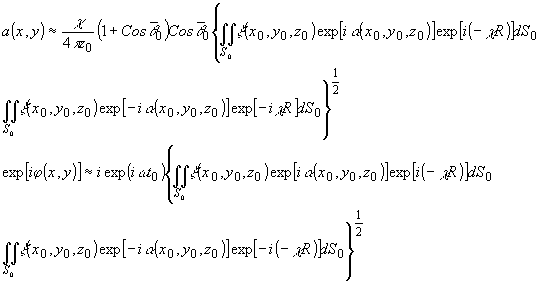 (4)
(4)
и
подставляя в (2).пользуясь принятым линейным соответствием
(3), получим:
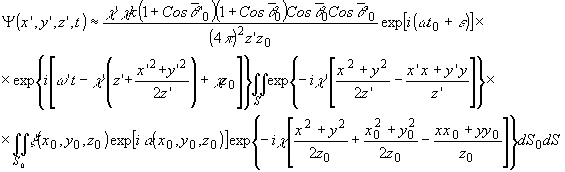 (2')
(2')
При
достаточно больших сравнительно с l областях интегрирования
S и S0 интегральный множитель можно представить
в виде
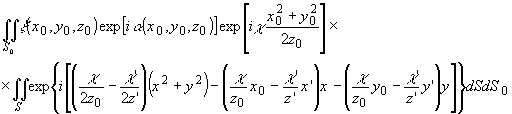
-
10 -
где
порядок интегрирования обращен. В выражении (2') нас будет
интересовать распределение поля на расстоянии z' = æ'z0/æ.
Так как коэффициент при квадратичном члене внутреннего интеграла
при этом обращается в нуль, то это условие в то же время
эквивалентно минимальной протяженности поля. В частном случае
æ' = æ этому соответствует распределение поля
на месте исходного объекта. При этом интегральный множитель
принимает вид;
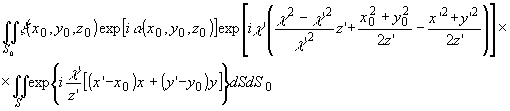
Здесь
внутренний интеграл в предельном переходе S ® ¥
можно выразить через импульсную d -функцию Дирака;
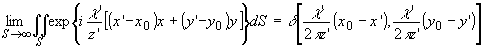
Воспользовавшись
известными свойствами d -функции /1/, - получим окончательное
выражение для (2'):
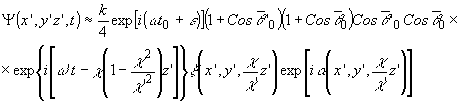 (2")
(2")
где средний
угол  '0 направления
на восстановленное изображение объекта выражается в виде
'0 направления
на восстановленное изображение объекта выражается в виде
-
11 -
Последнее
получено из условия минимальной протяженности поля z' = æ'z0/æ,
и простого геометрического соотношения 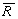 '20-
z'2 =
'20-
z'2 = 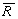 20
- z20.
20
- z20.
Из
выражения (2") следует, что сформированное поле по амплитуде
пропорционально полю исходного объекта и с точностью до
постоянного слагаемого модулировано по фазе подобно объекту.
Масштаб в продольном направлении трансформирован, при этом
член exp[-iæ(1 - æ2/æ'2)z']
описывает связанный с этим дополнительный сдвигфазы. Упомянутая
трансформация продольного масштаба связана с неравенством
длин волн, использованных при просвечивании объекта и смоделированной
по нему голограммы. При æ' = æ соответствующий
экспоненциальный член превращается в единицу и реконструированное
изображение оказывается идентичным исходному изображению
объекта.
Представляет
определенный интерес исследование информационного вклада
в формирование изображения раздельного отображения только
вещественной части (3) (амплитуда объектной волны) и только
мнимой ее части (фаза объектной волны). Мы рассмотрим обе
эти задачи.
Использовав
только первые уравнения (3) и (4) и подставив в (2), получим;
 (5)
(5)
Подкоренное
выражение вместе с интегральным множителем формально можно
переписать в виде /2/:
-
12 -
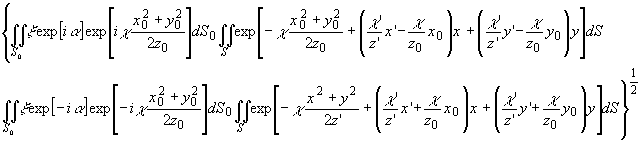
Решая
в подкоренном выражении интеграл по .получим для выражения
поля на расстоянии z' = æ'z0/æ.
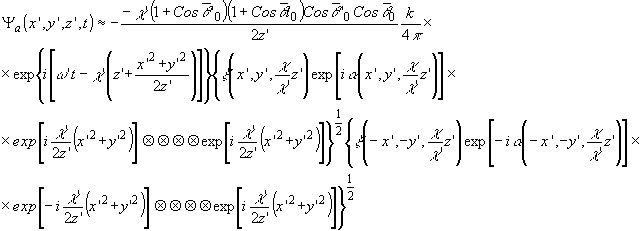 (5')
(5')
где
значок Ä Ä обозначает операцию двумерной свертки
/3/.
В
подкоренном выражении (5') стоит произведение двух сверток
объекта, соответственно, с положительным и отрицательным
сферическим искривлением с функцией exp{iæ(x'2+y'2)/2z'}.
Подобное сочетание операций иллюстрирует отсутствие полезной
информации в сформированном. поле. Исключение составляет
вырожденный случай
-
13 -
z'
= z0 = 0. Действительно, перепишем (5'), совершив
предельный переход с двух сторон z = ± æ'z0/æ
® 0, соответственно, для первой и второй части подкоренного
выражения:
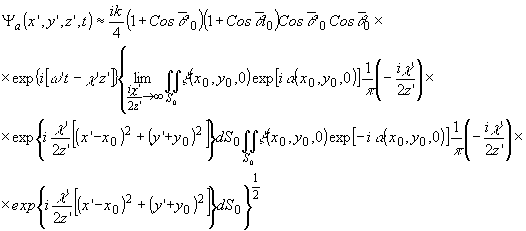 (5")
(5")
Использовав
выражение /1/:
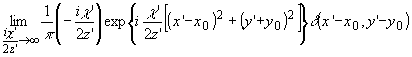
получим:
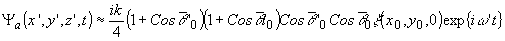 (5'")
(5'")
Полученное
выражение оказывается пропорциональным распределению амплитуды
по объекту. При этом информация о фазе полностью утеряна.
Рассмотрим
отображение на голограмме только фазовой части уравнений
(3) и (4). Здесь следует отметить, что эта идея впервые
была предложена Лиземом, Хоршом и Джорданом в 1969г. /4/.
Устройство, являющееся эквивалентом голограммы, им было
названо киноформом.
-
14 -
Для
дифрагированного киноформом поля получаем;
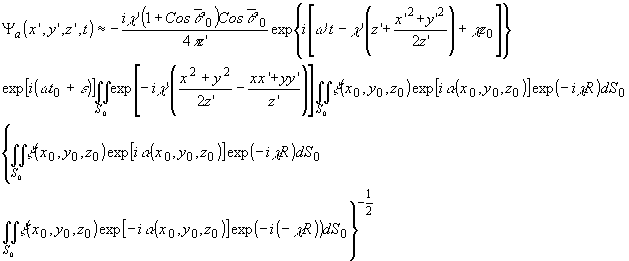 (6)
(6)
Используя
линейное приближение экспоненциального выражения в подкоренном
выражении и приближенно извлекая корень, получим:
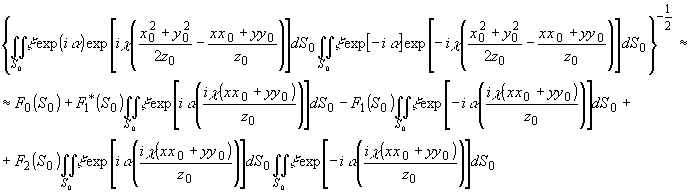
где
введены обозначения:
-
15 -
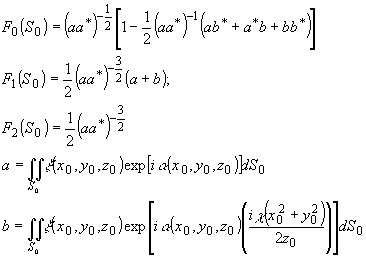
Первый
член приведенного выше разложения при подстановке в (6)
умножается на интегральные сомножители по S и S0
и при z' = æ'z0/æ дает член, пропорциональный
реконструкции объекта. Анализ интегральных множителей последующих
членов дает
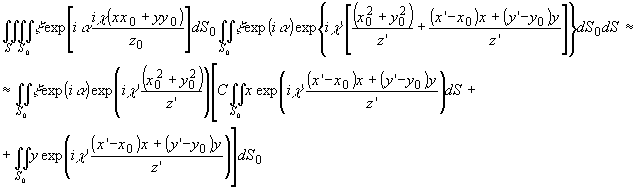
где
обозначено
-
16 -
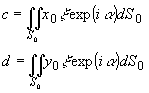
Интегралы
по S в этом члене выражаются в виде
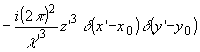 и
и 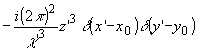
где
введены производные d -функции по соответствующим переменным.
Воспользовавшись
свойствами d -функции и ее производной для второго
и третьего интегрального множителя получим:
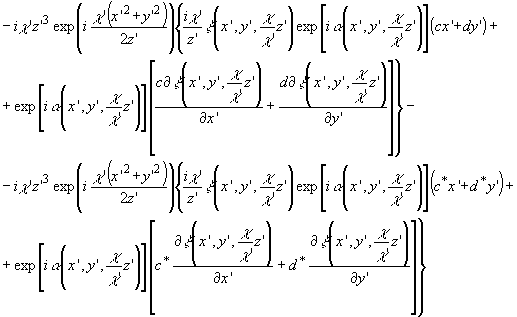
Аналогично
для четвертого интегрального множителя -
-
17 -
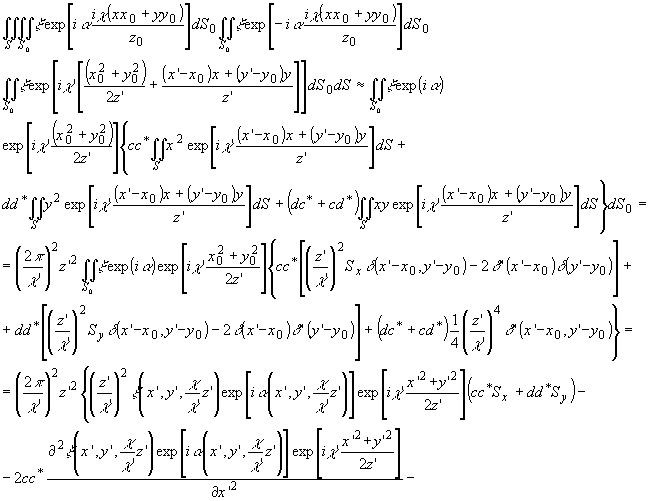
-
18 -
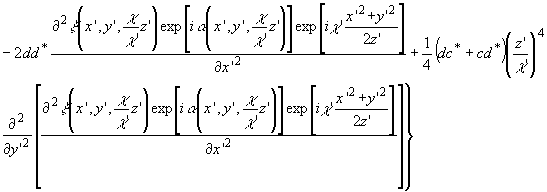
Здесь
Sx и Sy - максимальные линейные протяженности
области S по соответствующим координатам.
Использовав
выражения для интегральных множителей подкоренного члена,
выпишем окончательный вид реконструированного поля:
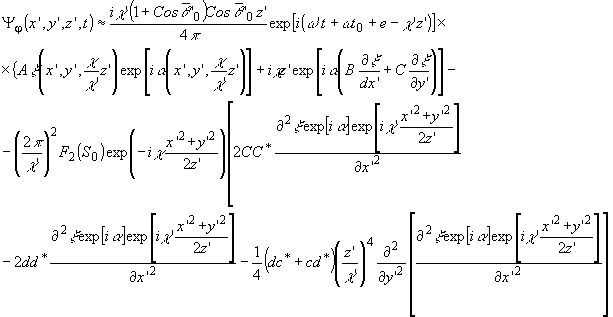 (6')
(6')
где
из соображений уменьшения громоздкости введены обозначения
-
19 -
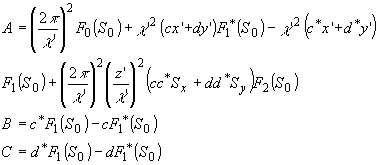
Как
и в рассмотренном выше выражении (2"), первый член в (6')
в фигурных скобках при z' = æ'z0/æ,
описывает реконструированное изображение (в пренебрежении
множителем z'). Последующие члены содержат частные производные
первого и более высоких порядков по координатам х', y' объекта.
При наложении на полезное изображение эти поля существенно
искажают его.
Очевидно,
причиной возникающих искажений является пренебрежение вещественной
частью комплексной амплитуды рассеянного объектом поля в
процессе конструирования киноформа. Подобное пренебрежение
возможно только для узкого класса объектов, формирующих
недиффузные поля, каковыми, в частности .являются безаберрационные
объективы. Только при этом имеет место поточечное равенство
подкоренного выражения, постоянное по величине(см. уравнение
(6)).
Учет
как действительной, так и мнимой частей рассеянного объектом
поля был использован в (2). Подобное устройство, отображающее
комплексную амплитуду объектного поля, в работе /5/ было
названо копифильтром (Complex Optical Phase - Implemented).
Это название не получило распространения. В ряде поздних
работ в качестве названия идентичных устройств вводятся
различные аббревиатуры, например, ROACH (Referenceless On-Axis
Complex Hologram /3/). В данной работе мы используем название
комплексный киноформ, представляющееся более содержательным,
в качестве
-
20 -
синонима
голограммы не формирующей побочных изображений.
Идею
комплексного киноформа можно распространить для n длин волн
и получить возможность отображения и последующей реконструкции
цвета наряду с комплексной амплитудой объекта. Подобная
способность киноформа была бы аналогичной свойствам толстослойных
голограмм /6/.
Действительно,
поле когерентного полихроматически излучающего объекта записывается
в виде
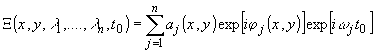 (7)
(7)
или
в интегральной форме с использованием квадратичного приближения
для расстояний:
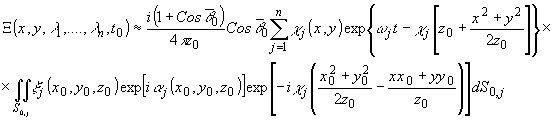 (7')
(7')
При
реконструкции этого поля белым светом или же исходным полихроматическим
набором длин волн должна использоваться среда с выраженной
селективностью спектрального пропускания. Точное выполнение
этого требования чрезвычайно ваяно для исключения перекрестной,
модуляции соседних частот, приводящей к возникновению ложных
изображений.
Сформулированное
требование можно описать системой уравнений, сопоставляющей
параметрам рассеянного объектом поля характеристики среды
киноформа:
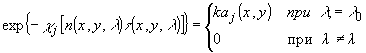 (8)
(8)
-
21 -
exp[-iæjn(x,y,l
)] = exp{i[j j(x,y)
+ e ]}; l = l j
Эта
система обобщает систему (3) на случай n-длин волн.
Воспользовавшись
(8), после просвечивания киноформа исходным набором длин
волн единичных aмплитyд получим:
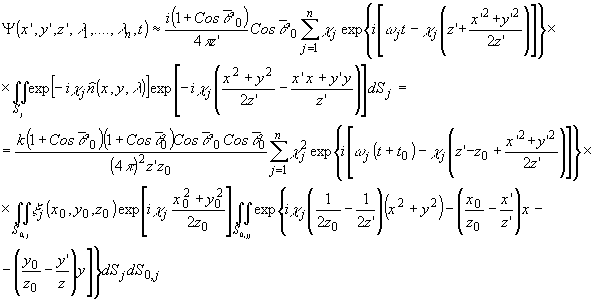 (9)
(9)
Поступая
так же, как и при анализе выражения (2") (когда z' = z0) и, как следует
отсюда, получаем Cos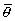 '0
= Cos
'0
= Cos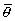 0.
0.
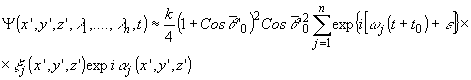 (9)
(9)
Из
анализа полученного выражения следует, что, распространяя
идею комплексного киноформа на n-длин волн при условии спектральной
селективности пропускания среды киноформа в соответствующих
-
22 -
областях
спектра, можно отобразить комплексное полихроматическое
поле объекта и реконструировать его n-цветное изображение.
Представляет
значительный интерес вопрос физической реализации комплексного
киноформа. Является очевидным, что амплитудная часть информации
о рассеянном объектом волновом поле может быть отображена
непосредственным фотографированием этого поля при надлежащем
выборе коэффициента конкретности, зернистости и методов
обработки светочувствительной среды, например, используя
фотопозитивный процесс. Аналогичная фотографическая регистрация
информации о мгновенном фазовом состоянии поля для электромагнитных
волн, однако оказывается нереализуемой. С другой стороны,
отображая относительную фазу единственно доступным в настоящее
время интерферометрическим способом, легко убедиться, что
возникающая при этом картина поточечного распределения интенсивности
неоднозначна. Действительно, каждому значению суммарной
интенсивности объектной и эталонной волны в данной точке
интерференционного поля могут соответствовать два состояния
относительной фазы исследуемого фронта. На рис.2 значению
суммарной интенсивности I, соответствуют одновременно D
j 1 и D j '1.
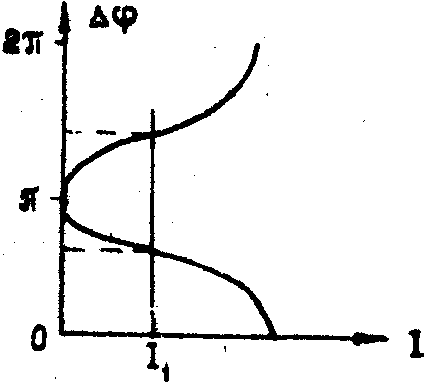
Рис.2.
Возникающая
неоднозначность может быть исключена только учетом окрестной
информации о распределении D j
или, что равнозначно, дополнительными измерениями по интерференционному
поле, например, прослеживанием линий равных фаз, использованием
нескольких длин волн и пр. По-видимому, в настоящее время
не известны физические процессы или явления, посредством
которых, без вмешательства
-
23 -
оператора,
было бы возможно поточечно разрешать возникающую неоднозначность
информации об относительной фазе и адекватно отображать
ее на материальном носителе. Подобное положение дел не оставляет
надежды на возможность создания комплексного киноформа путем
фоторегистрации рассеянного объектом волнового поля. Это
предопределило развитие машинных методов расчета и поточечного
моделирования некоторых практически важных случаев киноформов.
Несмотря на недостаточную технологичность и значительные
экспериментальные трудности, эти методы в ряде случаев оказываются
целесообразными.
Забегая
несколько вперед, отметим, что изложенное в последнем абзаце
относится только к скалярной теории. К этой проблеме мы
вновь вернемся при рассмотрении векторно-поляриэационных
методов, использование которых создает условие для положительного
разрешения поставленной задачи.
Двухмерная
голограмма
Проблема
неоднозначного отображения относительной фазы, имеющая место
при фоторегистрации результата интерференции с эталонной
волной, была частично обойдена в асимметричной схеме двухлучевой
голографической записи /7/. В этой схеме не несущие полезной
информации побочные изображения пространственно отделены
от реконструкции. Сам факт их возникновения тесно связан
с упомянутой проблемой неоднозначной записи фазы. Очевидно,
что низкий сравнительно с комплексным киноформом к.п.д.
подобной голограммы обусловлен существованием этих побочных
изображений.
Проблема
влияния характеристик регистрирующей среды на реконструированное
изображение исследовалась в ряде работ (см., например, /8/).
Здесь рассмотрен наиболее общий случаи амплитудно-фазовой
модуляции голограммной среды в случае тонкой голограммы.
Использованный подход был одним из первых последовательных
применений соответствующего математического аппарата /9/.
На
рис.3 рассеянное объектом поле перекрывается с опорной волной,
распространяющейся вдоль z в плоскости z = 0, где расположен
голограммный носитель S.
-
24 -
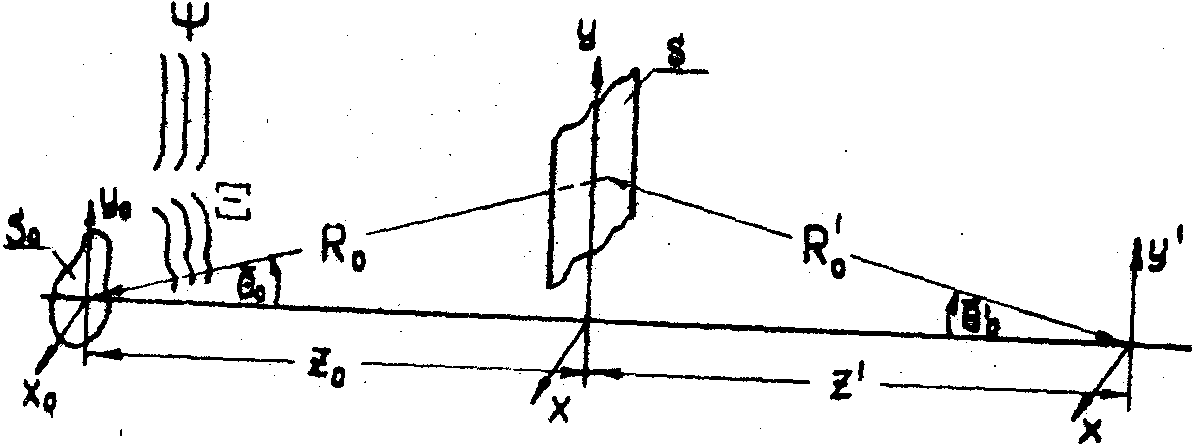
Суммарное
поле в голограммной плоскости складывается из двух компонент
y и X , где y = y оexp[ia
]exp[i(w t - æz) опорная, а
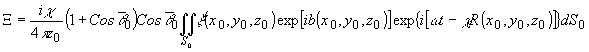
объектная
волны.
Наблюдаемой
величиной в скалярной теории является плотности электрического
поля w l или отождествляемая с вектором
Пойтинга <S> интенсивность. Здесь и в дальнейшем будет
рассматриваться лишь компонент электромагнитного волнового
поля. Подобное предпочтение связано с преобладающей его
ролью в процессах взаимодействия света с веществом.
Имеем:
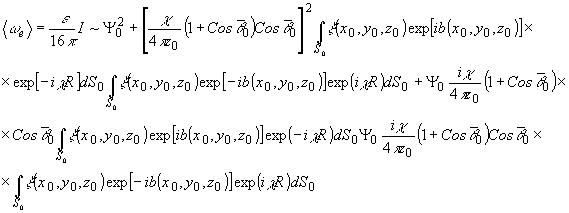 (10)
(10)
-
25 -
После
подстановки степенного ряда в предыдущее разложение подучим:
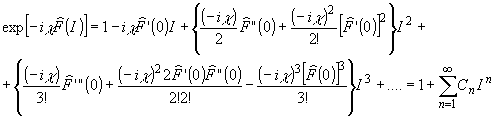
где
Сn выражается посредством коэффициентов разложения
обоих рядов в виде: c1=a1b1;
c2=а2b1+a21b2,
c3=a3b1+2a1a2b2+а31b3,
с4=а4b1+a22b2+2a1a3b2+3a21a2b3+а41b4;
Воспользовавшись
(12), можно представить поде, формируемое n-м членом выражения
(11), в виде:
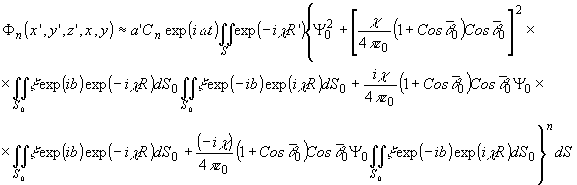
где
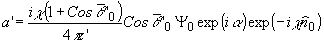
-
26 -
В общем
случае результирующая интенсивность отображается на голограммной среде в процессе
фоторегистрации нелинейно. При этом под воздействием поля имеет место комплексное
изменение первоначальных характеристик среды 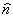 (х,
у) -
(х,
у) - 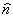 0 =
0 = 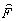 (I),
где
(I),
где 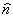 0 - исходный
комплексный коэффициент преломления среды (постоянный для однородной среды),
0 - исходный
комплексный коэффициент преломления среды (постоянный для однородной среды),
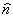 - конечный комплексный
коэффициент преломления,
- конечный комплексный
коэффициент преломления, 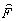 = n(I) + iu (I) - комплексная функция реакции среды на воздействие суммарного
поля (n(I) - связана с изменением коэффициента преломления, u (I) - с изменением
экстинции).
= n(I) + iu (I) - комплексная функция реакции среды на воздействие суммарного
поля (n(I) - связана с изменением коэффициента преломления, u (I) - с изменением
экстинции).
Просветив
зафиксированную на голограмме картину исходной опорной волной,
получим:
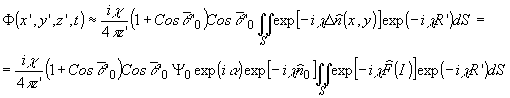 (11)
(11)
где
смысл введенных величин аналогичен использованным при рассмотрении
киноформа.
Разложим
подынтегральную функцию в известный ряд:
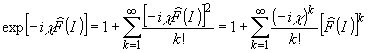
и аппроксимируем
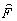 (I) степенным рядом в окрестностях
точки I = 0, где
(I) степенным рядом в окрестностях
точки I = 0, где 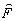 = 0:
= 0:
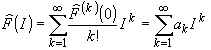
-
27 -
Представим
n-ую степень подынтегрального четырехчлена
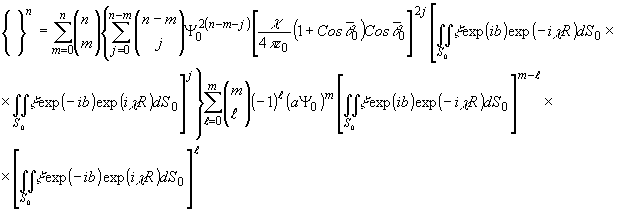
где 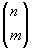 - биноминальные коэффициенты; ф = iæCos
- биноминальные коэффициенты; ф = iæCos 0Cos
0Cos 0/4p
z0.
0/4p
z0.
Заменив
в последнем разложении степень интеграла по n интегралом
соответствующей кратности с введением новых переменных .
и используя квадратичное приближение расстояний R и R',
перепишем (13):
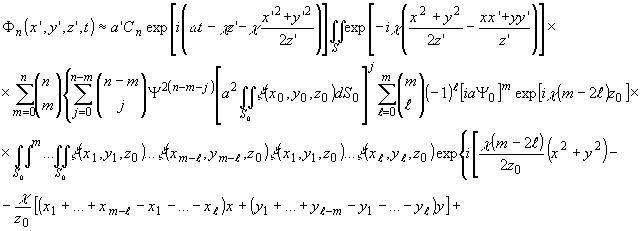
-
28 -
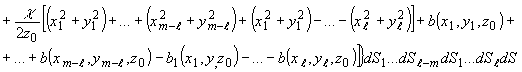
Обращая
порядок интегрирования по областям S и S0, для
m - члена предыдущего выражения получим:
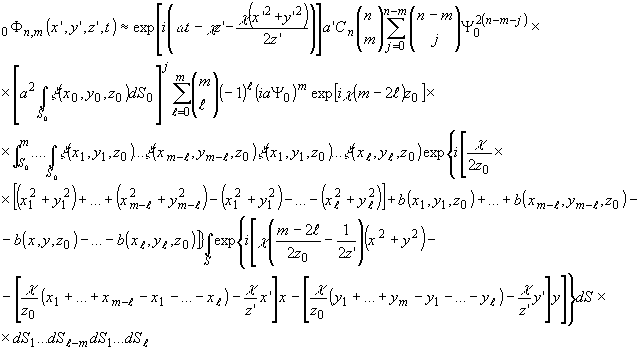 (14)
(14)
Рассмотрим
значение поля при индексах l, удовлетворяющих условию m-2l
=0. Это условие, очевидно, имеет место для четных m:
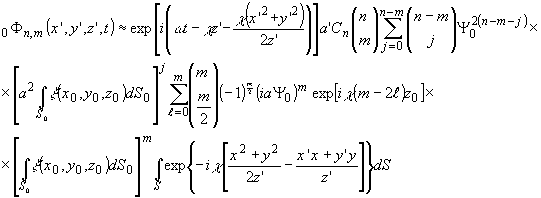 (14')
(14')
-
29 -
Решая
последний интеграл в асимптотическом приближении можно написать
для суммарного вклада подобного вида членов разложения
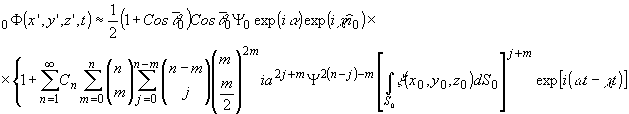 (15)
(15)
Анализ
полученного выражения показывает, что в нем информация об
объекте не содержится. Это прошедшая без дифракции часть
реконструирующей (опорной) волны ограничивается контурами
голограммы.
В
общем случае m-2l ¹ 0 рассмотрим поле на расстоянии
z', удовлетворяющем условию
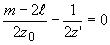
при
этом интеграл S в (14) вырождается в d -функцию.
Для
m-2l > 0 имеем:
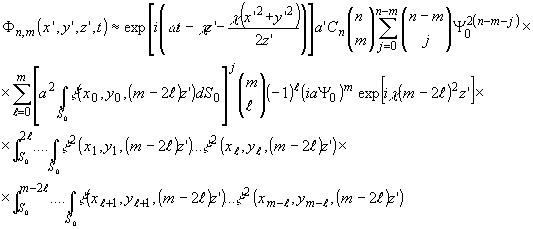 (14")
(14")
-
30 -
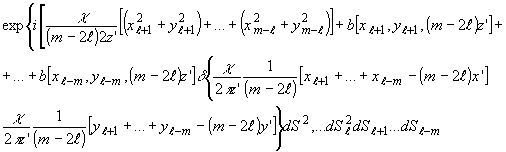
Для
m-2l < 0 имеем;
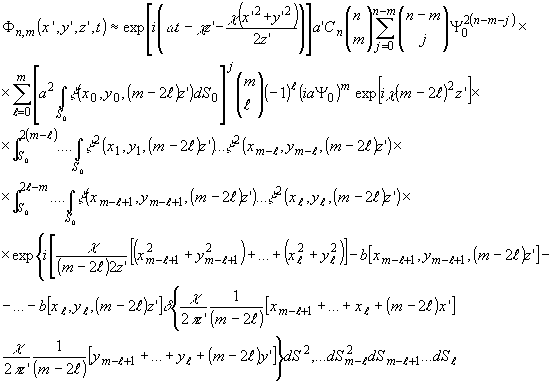 (14'")
(14'")
Воспользовавшись
известными свойствами d -функции, получим, соответственно,
для (14") и (14'''):
-
31 -
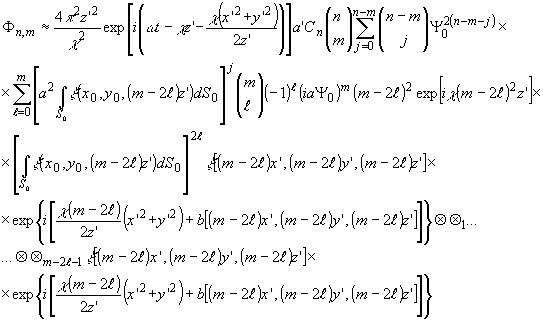
и
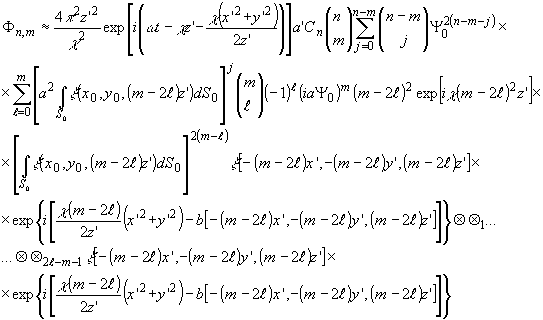
Из
(14") и (14'") следует, что ими описываются дифрагированные
компоненты, представляющие последовательности двухмерных
сверток изображения объекта с собой с продольными и поперечными
масштабными преобразованиями (m-2l) - кратности и с соответственно
масштабно трансформированной фазой. Кроме того, имеет место
-
32 -
дополнительное
сферическое искривление 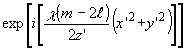 и линейное искажение фазы как функции (m-2l)2. Средний угол направления
дифрагированной волны равен
и линейное искажение фазы как функции (m-2l)2. Средний угол направления
дифрагированной волны равен
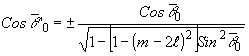
Знак
+ берется для (14"), знак - берется для (14'").
Исследуем
результирующее поле при значениях индекса l = 0 для m-2l
> 0. Имеем
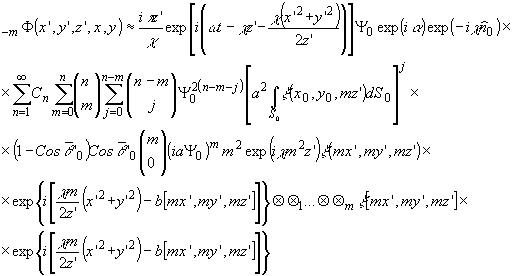 (16)
(16)
где
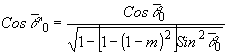
При
значении индекса l = m для m-2l < 0 получим:
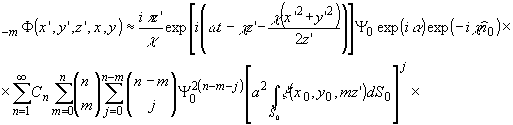 (16)
(16)
-
33 -
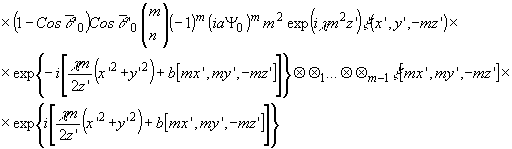
где
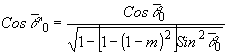
Выражения
(16) и (17) описывают компоненты высших порядков, дифрагированные
симметрично по обе стороны от нулевого порядка. Элементарный
анализ показывает, что в них полезная информация не содержится.
Отбор порядков с данным направлением дифракции возможен
при фиксировании m1 являющимся одновременно индексом
порядка.
Существенно
важным является результирующее поле при значениях индексов
l= (m-1)/2 для (14") и l = (m+1)/2 для (14"'). При l = (m-1)/2
имеем:
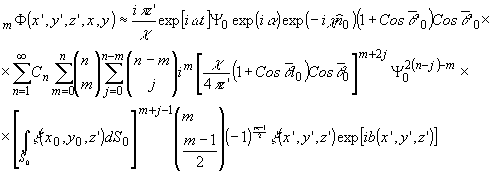 (18)
(18)
Cos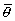 '0
= Cos
'0
= Cos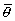 0
0
-
34 -
При
l = (m+1)/2 имеем:
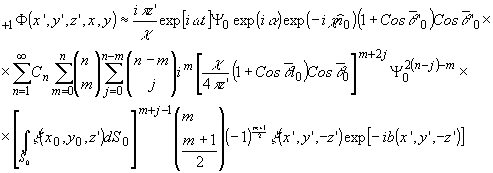 (19)
(19)
Cos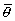 '0
= -Cos
'0
= -Cos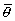 0
0
Из
(18) следует, что описываемое им поле с точностью до постоянного
множителя модулировано подобно полю объекта. Это мнимое
изображение-- реконструкция поля объекта.
Выражение
(19) описывает действительное изображение, являющее собой
псевдоскопический аналог реконструкции поля объекта.
Полученные
.выражения в наиболее общем виде описывают связь восстановленного
поля с комплексной реакцией среды и амплитуды опорной и
объектной волн. Они могут быть использованы для нахождения
оптимальных значений этих параметров при решении различных
задач, например, достижения максимальной дифракционной эффективности.
Поляризационный
киноформ
Рассмотрение,
проведенное в предыдущих разделах, основано на скалярной
теории электромагнитных волн. Однако, задачи, сформулированные
в таком виде, оказываются в ущербном положении, т.к. не
-
35 -
учитывается
поперечно- колебательный характер света - состояние его
поляризации. Последнее, однако, является фундаментальной
характеристикой волнового поля электромагнитных волн.
Обобщение
теории голографии на поляризацию проведено в работе /10/
(см., также. Материалы V, VII, IХ школ по голографии), и
на ней останавливаться не будем. Здесь будет проведено .
аналогичное обобщение теории для киноформа.
Векторное
поле объекта в плоскости наблюдения Z = 0 в момент времени
t0 можно записать в параксиальном приближении
в виде вектор - столбца Джонса /11/:
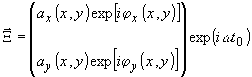 (20)
(20)
Для
возможности последующего воспроизведения этого поля информация
о его фазе и амплитуде должна быть отображена на материальном
носителе и проведено его облучение реконструирующей волной.
Аналогично
упомянутой скалярной теории киноформа, в которой мгновенному
распределению скалярного волнового поля вводится в соответствие
вариация комплексного коэффициента преломления изотропной
среды киноформа, в данной работе мгновенному распределению
векторного поля сопоставляется вариация комплексного коэффициента
преломления анизотропной среди. Таким образом, проблема
отображения скалярной комплексной амплитуды на изотропном
носителе трансформируется в проблему отображения векторной
комплексной амплитуды на анизотропном носителе.
Здесь
мы также ограничимся реконструирующей волной с плоским фронтом,
направленной нормально к плоскости носителя. В отличие от
скалярного случая, здесь характеристики поляризации реконструирующей
волны выступают в качестве дополнительных свободных параметров.
-
36 -
Если
поляризационный комплексный киноформ организован описанным
выше способом, то поле за ним при его просвечивании плоской
волной заданной поляризации может быть представлено в форме
векторного дифракционного интеграла Кирхгофа:
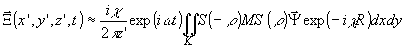 (21)
(21)
где R(х,у,х',у',z')
- расстояние от точки поверхности киноформа x,у до точки наблюдения х',у',z':
М = 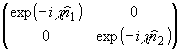 - матрица Джонса анизотропного
участка киноформа, обобщенная на комплексный коэффициент преломления, S(r
)=
- матрица Джонса анизотропного
участка киноформа, обобщенная на комплексный коэффициент преломления, S(r
)=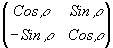 и S(-r )=
и S(-r )=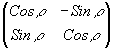 матрицы прямого и обратного поворота (r - азимут ориентации оси наибольшей
скорости анизотропного элемента;
матрицы прямого и обратного поворота (r - азимут ориентации оси наибольшей
скорости анизотропного элемента; 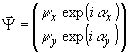 - вектор-столбец просвечивающего (реконструирующего)света. Интегрирование ведется
по плоскости K, занятой киноформом.
- вектор-столбец просвечивающего (реконструирующего)света. Интегрирование ведется
по плоскости K, занятой киноформом.
В приведенном
выражении (21) компонент S(-r )MS(-r )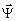 описывает поле непосредственно за киноформом. Представим его как произведение
действительного
описывает поле непосредственно за киноформом. Представим его как произведение
действительного 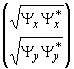 и мнимого
и мнимого
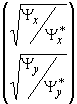 вектор-столбцов, где
вектор-столбцов, где
Y
x = y xеxр(ia x)[Cos2r
·ехр[-iæn1(1-it 1)]
+ Sin2r ·eхр[-iæn2(1-it
2)] +
+
y yеxр(ia y)Cosr Sinr
[exр[-iæn1(1-it 1)] - eхр[-iæn2(1-it
2)]
Y
y = y yеxр(ia y)[Sin2r
·ехр[-iæn1(1-it 1)]
+ Cos2r ·eхр[-iæn2(1-it
2)] +
+
y xеxр(ia x)Cosr Sinr
[exр[-iæn1(1-it 1)] - eхр[-iæn2(1-it
2)]
Приравняв
действительные и мнимые часта, соответственно, рассеянного
объектом и сформированного поляризационным киноформов полей,
получим систему векторных уравнений, в которой использован
факт реконструкции:
-
37 -
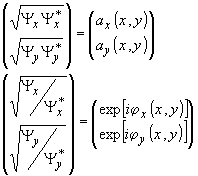 (22)
(22)
Полученная
система может быть проанализирована с двух позиций: во-первых?
для выражения анизотропных характеристик среды киноформа
через параметры объектного и реконструирующего полей, и,
во-вторых, для решения в некотором смысле обратной задачи
-определения класса объектных полей, реконструкция которых
возможна при выбранном законе отображения характеристик
на киноформе.
Из
постановки первой задачи сразу следует, что, выражая n2,
n1t 1, n2t 2, r через
параметры объектного и реконструирующего волновых полей,
мы должны одну из этих характеристик принять в качестве
свободного параметра, так как (22) представляет собой систему
четырех уравнений.
Положив
r = Const, мы можем рассмотреть поляризационный киноформ
с постоянной по поверхности ориентацией оси анизотропии.
Анализ полученной системы показывает, что в общем случае
. решение дает 256 четверок значений n1, n2,
n1t 1, n2t 2. Мы значительно
упростим систему: выбрав для иллюстрации два случая, r
= 0 и r = p /2.
Опуская
громоздкие вычисления, выпишем конечный результат при r
= 0:
exp(-iæn1)
= exp{i[j x(x,y)
- a x]; exp(-æn1t
1) = ax(x,y)/y x
exp(-iæn2)
= exp{i[j y(x,y)
- a y]; exp(-æn2t
2) = ay(x,y)/y y
-
38 -
при
r = p /2:
exp(-iæn1)
= exp{i[j y(x,y)
- a y]; exp(-æn1t
1) = ay(x,y)/y y
exp(-iæn2)
= exp{i[j x(x,y)
- a x]; exp(-æn2t
2) = ax(x,y)/y x
Таким
образом, при выбранной оси анизотропии r = 0 распределение
каждой компоненты анизотропного коэффициента преломления
равно функции фазы объектного поля минус функция фазы реконструирующего
поля. Аналогично связаны компоненты анизотропной экстинкции
с логарифмами амплитуд объектной и реконструирующей волн.
Для соответствующие компоненты по координатам меняются местами.
Частным
выводом из вышесказанного следует принципиальная возможность
поточечной реализации поляризационного киноформа на монокристаллах,
обладающих способностью к фотоанизотропии. Выбор конкретных
сред и мощности поточечной засветки может обеспечить нужное
соответствие анизотропных коэффициентов преломления и экстинкции.
В отличие от /11/, где фотоанизотропный кристалл используется
для формирования скалярного киноформа, описанным путем возможно
создание поляризационного киноформа, способного воссоздать
векторное поле объекта.
Не
задаваясь целью решить всю систему возможных вариантов уравнений
поляризационного киноформа, рассмотрим два случая .навеянных
аналогиями со скалярным комплексным киноформом.
Положив
n1t 1 = n2t 2 = 0, мы переходим
к рассмотрению условий, в которых возможно осуществление
чисто двулучепреломляющего киноформа. Анализ первой векторной
системы (32) при атом приводит к выражению:
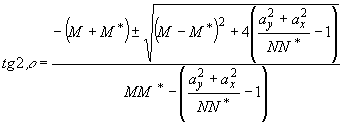 (23)
(23)
-
39 -
Решение
второй векторной системы (22) дает:
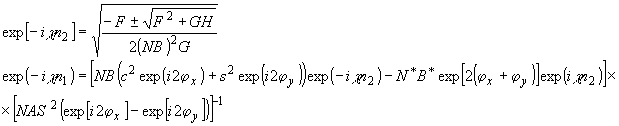 (24)
(24)
где
с целью уменьшения громоздкости выражений введены обозначения:
C
= Cosr ; S = Sinr ; М = y y·ехр[i(a
y-a x)]/y x; N
= y xехр(ia x);
A
= C(C + MS); B = S(S-MC)
F
= 2N2C-2exp(i2a y)[4S2(S2A-C2B)(exp(i2a
x)-exp(i2a
y))2
+
+
B2C2exp(i2a x)(c2exp(i2a
x)
+ s2exp[i2a y])(s2exp[i2a
x-c2exp[i2a
y]);
G
= (c2exp[i2a x]
+ s2exp[i2a y])[s2(exp[i2a
x]-exp[i2a
y])2
-
-
c-2(c2exp[i2a x]
+ s2exp[i2a y])(s2exp[i2a
x-c2exp[i2a
y]);
H
= 4C-4(NN*BB*)exp[i4(a
x
+ a y)](s2exp[i2a
x]
+ c2exp[i2a y])
Рассмотрим
возможность существования чисто дихроичного киноформа. Положив
n1 = n2 = n – Const, получим из второй
векторной системы (22)
-
40 -
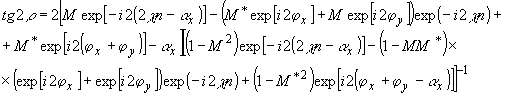 (25)
(25)
Из
первой векторной системы (22) следует:
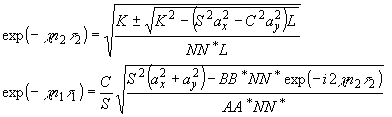 (26)
(26)
где
введены обозначения
K
= | B| 2S-2(S2
– C2)(S2a2x
- C2a2y) + 2| A|
-2C2(AB*
+ A*B)(a2x + a2y)
L
= | B| 4S-4(S2
- C2) 2 + | B| 2S-2C2(AB*
+ A*B)
Показанная
здесь возможность существования как чисто двулучепреломляющего,
так и чисто дихроичного киноформа для произвольного объектного
поля представляет принципиальный интерес. Для сравнения
следует упомянуть, что в скалярной теории, изображение,
формируемое чисто фазовым киноформом, существенно искажено
(см. (6')), возможность же существования чисто амплитудного
киноформа полностью исключена. Кроме того, в случае скалярного
комп -лексного киноформа каждому реконструированному полю
соответствует единственное, с точностью до постоянного,
распределение комплексного коэффициента преломления. В случае
поляризационного
-
41 -
киноформа
это соответствие многозначно: заданному векторному полю
сопоставлено множество решений системы (22). Так, для киноформа
с выбранной осью анизотропии существует 256 равноценных
четверок n1, n2, n1t 1,
n2t 2. Легко видеть, что это положение вы
-звано нелинейна, характером основной системы.
Можно
предположить, что в будущем, при создании поляризационного
киноформа машинными методами подобная многозначность может
быть использована для выбора подходящих алгоритмов реализации
из существующего набора решений, а также для оперативного
перехода от одной системы решений к другой.
Коснемся
важного вопроса физической реализации комплексного киноформа.
Существующие методы в основном повторяют использованную
в /4/ идею поточечного моделирования на киноформе фазы,
а в общем случае - комплексной амплитуды объектной волны
/12/. Подобное моделирование осуществляется на светочувствительном
носителе, который поточечно засвечивают по заданной ЭВМ
программе и далее подвергают последующей обработке. Этот
путь реализации киноформа связан с принципиальными ограничениями
объема регистрируемой информации.
В
работе /13/ показано, что при поляризационной голографической
записи с использованием наведенной светом анизотропии в
случае опорной волны циркулярной поляризации действительное
изображение не формируется. Этот вывод теории был подтвержден
экспериментально.
Подобная
голограмма при надлежащем выборе фотоанизотропной среды
и условий записи фактически является комплексным киноформом,
полученным голографическим путем для волновых полей типа
объектное + опорное поле. При этом побочных изображений
не формируется.
Исходя
из приведенного примера, можно поставить задачу получения
поляризационного киноформа голографическим путем и определить
класс реконструируемых таким путем векторных волновых полей.
Выбрав
в качестве закона отображения поля на киноформе количественную
меру фотоиндуцированной анизотропии /10/ и подставив его
в (22), получим систему четырех уравнений, где неизвестными
-
42 -
являются
параметры векторного волнового поля ах, ау,
j х, j у.
Выпишем
количественную меру фотоиндуцированной анизотропии для плоского
наведения в виде:
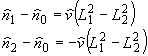 (27)
(27)
где
v = k + iℓ (k, ℓ - коэффициенты векторного отклика
среды, соответственно, для n и t ); L21
и L22 - энергетические характеристики
воздействующего на среду света, интенсивности большой и
малой осей эллипса поляризации.
Выпишем
также векторное поде объекта в плоскости z = 0 в виде
 =
= 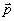 Cosw t +
Cosw t + 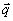 Sinw
t (28)
Sinw
t (28)
где
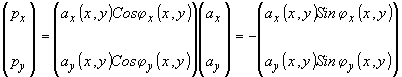
связаны
с параметрами светового эллипса соотношениями:
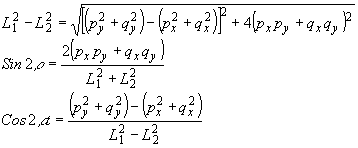 (29)
(29)
(r
- азимут ориентации большой оси светового эллипса).
Выражая
анизотропные характеристики среды 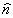 1
и
1
и 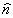 2 посредством
(27) и воспользовавшись (28), (29) при подстановке в (22), получим систему,
решение которой при выбранном
2 посредством
(27) и воспользовавшись (28), (29) при подстановке в (22), получим систему,
решение которой при выбранном 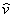 и состояния поляризации реконструирующей волны позволит найти класс волновых
полей, запись которых возможна голографическим способом.
и состояния поляризации реконструирующей волны позволит найти класс волновых
полей, запись которых возможна голографическим способом.
В
качестве иллюстрации приведем модефицированную таким
-
43 -
образом
систему (22) для циркулярно поляризованной реконструирующей
волны
y
х = y y = 1; a y
- a x = p /2.
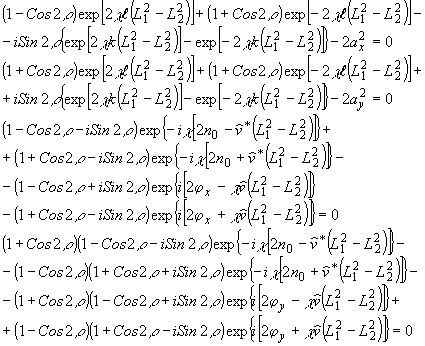
Приведенная
в качестве примера система трансцендентна. Решение ее получается
методами приближенных численных вычислении. Этот анализ
мы здесь проводить не будем. Мы имели целью показать, что
решение как прямой, так и обратной задачи теории
-
44 -
поляризационного
киноформа, имеет физический смысл. Прямая постановка задачи
служит для получения алгоритма, по которому проводится поточечная
обработка киноформа с целъю придания ему требуемых свойств
анизотропии. Реконструкция подобным киноформом позволяет
воспроизводить векторное волновое поле объекта. Обратная
постановка задачи служит для нахождения методов записи векторной
информации на киноформе, в частности, использующих наведение
фотоанизотропии. При этом целью подобного использования
является создание кииоформа голографическим способом. Последний
налагает ограничения на класс векторных объектных полей,
которые можно записать и реконструировать без образования
побочных, изображений. Поиск методов записи, позволяющих
реконструировать максимально широкий класс волновых нолей,
представляется предметом исследования этого подхода.
Таким
образом, введение состояния поляризации волнового поля в
качестве реконструируемого параметра существенно расширяет
функциональные возможности когерентных оптических устройств,
в частности, киноформа, и должно быть широко использовано
в системах оптической переработки информации.
В
данной лекции ставится ряд нерешенных задач (особенно в
последнем разделе), к разработке которых приглашается читатель.
Литература
1.
Э.Маделунг. Математический аппарат физики, ФМ, М., 1960.
2.
И.С.Градштейн и И.М.Рыжик. Таблицы интегралов, сумм, рядов
и произведений, "Наука", М., 1971.
3.
А.Папулис. Теория систем и преобразований в оптике. "Мир",
M., 1971.
4.
Лизем, Хорш, Джордан. Киноформ, Зарубежная радиоэлектроника,
12, 41-51, 1969.
5.
J.P.Kirk Laser Focus, N 6, 26, 1970.
6.
Ю.Н.Денисюк. ДАН СССР, 144, 1275, 1962.
-
45 -
7.
E.N.Leith, O.Upatnieks. JOSA, 52. 1123, 1962.
8.
H.Koegelnik. Proc. Sympos. Mod. Optics. New York, 1967.
9.
Ш.Д.Какичашвили. ЖТФ, 42, 1967, 1972.
10.
Ш.Д.Какичашвили. Опт. и спектр., 33, 324, 1972.
11.
У.Шерклифф. Поляризованный свет, "Мир", М., 1965.
12.
P.C.Chy., J.R.Fienup, J.W.Goodman., Appl.Opt., 12,
N 7, 1386, 1973.
13.
Ш.Д.Какичашвилн, Т.Н.Квинихидзе. Квантовая электроника.
2, № 7, 1449, 1975.

