|
|
 |
 |

|
| |
Аподизация
Профиль аппаратной функции, определяемой формулой (4), вносит значительные искажения в спектрограмме, особенно в случае регистрации структурных спектров. Поэтому для улучшения формы аппаратной функции применяют аподизацию 19) состоящую в умножении интерферограммы G*0(t) на некоторую оглаживающую функцию. В результате образуется новая интерферограмма
<G*(t)> = G*0(t)¦
(t) (6)
Обычно аподизация выполняется математически в процессе обработки интерферограммы G*0(t) на ЦВМ.
Рассмотрим частный случай, когда
¦ (t)=1-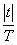 .
Подставив
(6) в
(1) и выполнив аналогичное
§ 7 интегрирование, мы найдём вид аппаратной
функции при аподизации: .
Подставив
(6) в
(1) и выполнив аналогичное
§ 7 интегрирование, мы найдём вид аппаратной
функции при аподизации:
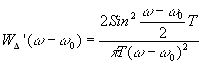 (7) (7)
Предел разрешения теперь увеличился в два раза: 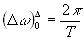 .
В волновых числах предел разрешения .
В волновых числах предел разрешения 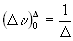 .
Переходя от модуляционных частот к волновым числам, аппаратную функцию найдём
в виде .
Переходя от модуляционных частот к волновым числам, аппаратную функцию найдём
в виде
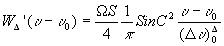 (8) (8)
Из этого выражения мы видим, что главный максимум аппаратной функции расширился в два раза и за счёт этого интенсивность в центре упала в два раза.
19) Этот термин уже давно применяется в оптике для обозначения способов улучшения качества изображений.
Кроме аподизацирующей функции "треугольной" формы, рассмотренной выше, применяются сглаживающие функции вида:
¦ 1(t) = SinC (10)
предложенные Стронгом и Ванассом /23/;
¦ 2(t) = 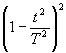 (10)
применявшиеся в работах Ж .Конн /61/.
Наконец, особый интерес представляет работа Филлера /89/, в которой предлагается проводить аподизацию с помощью интерполяционного ряда, выведенного на основе применения теоремы Котельникова; при этом существенно, что обработке подвергается не интерферограмма, а спектрограмма. Им также исследованы различные новые формы аподизирующих функций.
В этой связи важно отметить, что метод Филлера /89/ даёт возможность по необходимости применять разные аподизирующие функции, что позволяет получить дополнительную информацию. Это было использовано Ж. и П.Конн /53/ при обработке спектров Марса и Венеры.
В общем случае связь спектрограммы F
Т(w
) с исходным спектром F
(w
) через аппаратную функцию W(w
), представленную интегралом свертки,
F T(w
) º  (w
')W(w -w ')dw (w
')W(w -w ')dw
(11)
удобно рассматривать как усреднение F
(w
) в каждой точке по некоторому эффективному интервалу D
(w
)0, с заданной весовой функцией W(w
). Такое рассмотрение впервые было введено еще Релеем /90/ в 1912 году. Интересно заметить, что уравнение типа (11) выводится при анализе работы приёмно-регистрирующих систем не только в спектроскопии, но также в других областях /91/.
Исходя из этой точки зрения, применение аподизации эквивалентно усреднению спектрограммы, полученной без аподизации по эффективному спектральному интервалу. В частности, в Фурье-спектрометрии при конструировании аподизирующей функции в виде произведения нескольких функций получается результат, эквивалентный применению последовательного усреднения исходной спектрограммы с соответствующими весовыми функциями. Такое усреднение иногда имеет смысл применять для подавления фазовых искажений /92/.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

