ОБОБЩЕННЫЕ ГОЛОГРАММЫ
Л.М.Сороко
В лекции изложены следующие вопросы:
1. пространственная структура голограммы и требования к решающей способности фотоэмульсии;
2. голограмма Фурье и причины, позволяющие использовать для её получения крупнозернистые фотоэмульсии;
3. обобщённая голограмма, стадия восстановления для которой осуществляется с помощью дополнительного голографического фильтра.
Голографический метод позволяет полно и обратимо зарегистрировать амплитуду и фазу волнового поля в плоскости голограммы. По сравнении с фотографическим методом голография обладает существенными преимуществами, но они достигаются определённой ценой, а именно: регистрирующая среда, в которой получают голограмму, должна обладать более высокими параметрами по разрешающей способности, чем это требуется в обычной фотографии или в других передающих или отображающих неголографических системах.
Покажем, что в обычной схеме получения голограммы требования к разрешающей способности фотоэмульсии в самом общем случае повышаются в 4 раза. Так, например, если для регистрации волнового поля фотографическими средствами, т.е. с потерей фазовой информации, требуется разрешение в 100 л/мм, то при той же пространственной структуре волнового поля, но с условием, что теперь регистрируется также фазовая информация, необходимо перейти от 100 л/мм к 400 л/мм.
Это имеет существенное значение при передаче голограммы по каналам связи, так как фактор скорости передачи там является основным.
Итак, рассмотрим простейшую схему получения голограммы с использованием плоского опорного пучка. Пусть волновое поле в плоскости голограммы, которое должно быть зарегистрировано на голограмме, описывается оптическим сигналом u(x). Картина интенсивности, которая регистрируется фотоэмульсией, равна квадрату модуля полного волнового поля, состоящего из волнового поля предмета и поля опорного пучка (рис.1):
I(x)=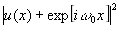 =1+u(x)u*(x)+
=1+u(x)u*(x)+
+u(x)exp[-iw
0x]+u*(x)exp[iw
0x] (1)
Последние два слагаемых ответственны за образование мнимого и действительного изображений на стадии восстановления. Если выполнить некоторые условия экспозиции и режима проявления фотоэмульсии, то можно добиться того, что амплитудное пропускание проявленной фотоэмульсии станет равным функции I(x) или же эта функция составит существенную часть амплитудного пропускания голограммы.
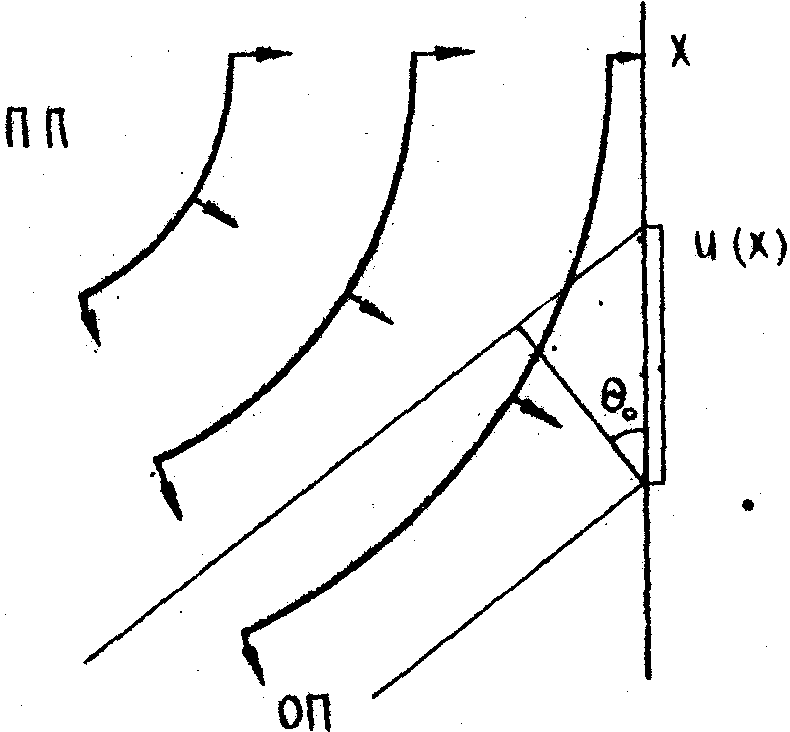
Рис.1. Схема получения голограммы волнового поля u(x) с помощью плоского опорного пучка, падающего на плоскость фотопластинки под углом q
0
При освещении голограммы прямой опорной волной, возникнет два боковых пучка, наклонённых относительно прямого опорного пучка под углом
± q
0 = ± 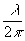 w
0 (2)
w
0 (2)
Волновое поле непосредственно за голограммой описывается оптическим сигналом
uвых(x)=1(x)I(x)=I(x) (3)
Это волновое поле, характеризуемое определённой пространственной структурой, претерпевает дифракцию, образуя на некоторой расстоянии от голограммы мнимое и действительное изображения. Пространственная структура волнового поля непосредственно за голограммой тождественна пространственной структуре функции I(х), т.е. распределению интенсивности, образующейся на стадии получения голограммы. Для того, чтобы проанализировать эту пространственную структуру, совершим переход от координаты х к направлениям по углам или к пространственным частотам w
. Наивысшая пространственная частота соответствует наиболее мелкой дифракционной решётке, и если удастся зарегистрировать такую решётку, то потери информации не произойдёт и задача голографирования будет выполнена полностью.
Проанализируем пространственную структуру функции uвых(х) подвергнув её преобразовании Фурье. Её Фурье-образ имеет вид:
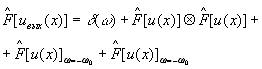 (4)
(4)
Первое слагаемое функции uвых(х) соответствует равномерной засветке, т.е. некоторой постоянной величине. Пренебрегая конечными размерами апертуры, предположим в нулевом приближении, что эта постоянная величина задана в интервале от -∞ до +∞. При преобразовании Фурье возникнет дельта-функция. Здесь использовано векторное обозначение аргумента}
w
º
(w
хw
у)
Двухмерная дельта-функция d
(w
) расположена в начале координат плоскости пространственных частот,
w
х = w
у = 0
Второе слагаемое в (1)
равно произведению двух функций, u(x)
и u*(x).
Воспользуемся тем, что операции умножения в обычной пространстве соответствует
операция корреляции или свёртки в частотном пространстве. Наконец, наличие фазовых
множителей exp[±
iw 0x]
в (1)
эквивалентно сдвигу Фурье-образа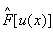 на
отрезки 0w 0
и w 00.
Иначе говоря, введение высокочастотной несущей перемещает спектр, как и в обычной
радиотехнике, в область высоких пространственных частот. Таким образом, двухмерный
Фурье-образ функции uвых(х)
имеет вид, показанный на рис.2.
на
отрезки 0w 0
и w 00.
Иначе говоря, введение высокочастотной несущей перемещает спектр, как и в обычной
радиотехнике, в область высоких пространственных частот. Таким образом, двухмерный
Фурье-образ функции uвых(х)
имеет вид, показанный на рис.2.
Рассмотрим простейший пример. Пусть функция u(х)
- одномерная действительная функция,
спектр которой имеет вид прямоугольного импульса (рис.3) шириной
2 W 0.
Второе слагаемое в (4) -
корреляция прямоугольного импульса -
имеет вид треугольного импульса с шириной, вдвое большей ширины прямоугольного
импульса, т.е. 4W 0.
Последние два слагаемых в (4)
получаются путём сдвига прямоугольного импульса 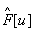 на величину +w
0,
вправо и на -w
0
влево. Окончательно Фурье-образ uвых(х)
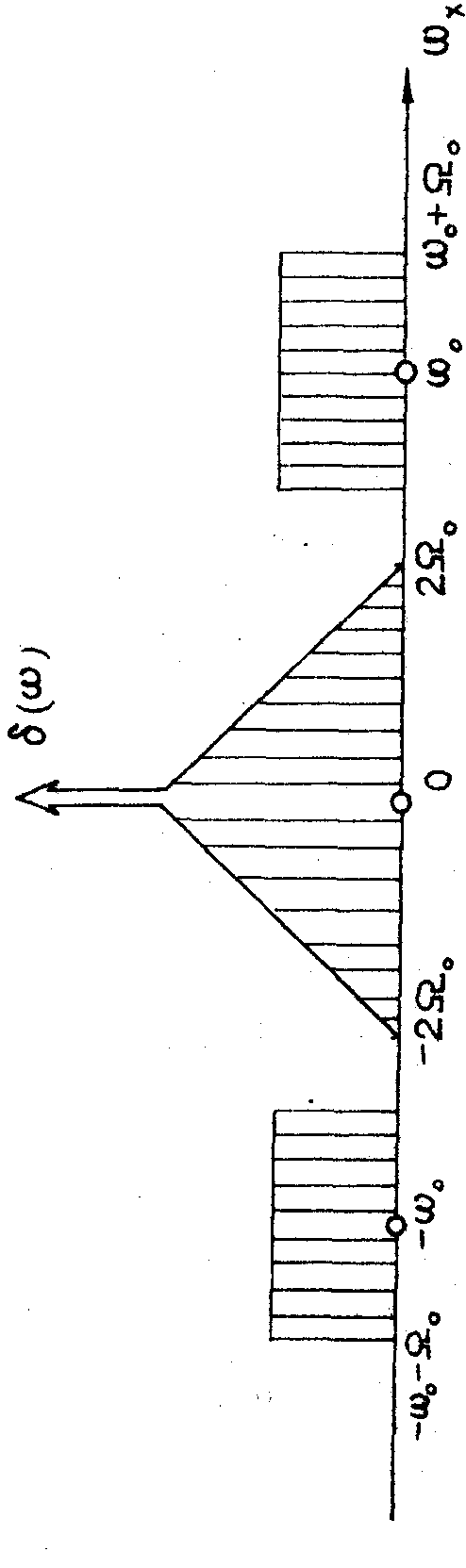
примет следующий вид (рис.4). Вблизи
дельта-функции, соответствующей средней засветке голограммы, располагается вредная
составляющая -
автокорреляция функции u(х).
Полезные компоненты, несущие неискаженную
информацию о волновом поле uвых(х),
располагается около частот
на величину +w
0,
вправо и на -w
0
влево. Окончательно Фурье-образ uвых(х)
примет следующий вид (рис.4). Вблизи
дельта-функции, соответствующей средней засветке голограммы, располагается вредная
составляющая -
автокорреляция функции u(х).
Полезные компоненты, несущие неискаженную
информацию о волновом поле uвых(х),
располагается около частот
w
1 = -w
0 и w
2 = +w
0
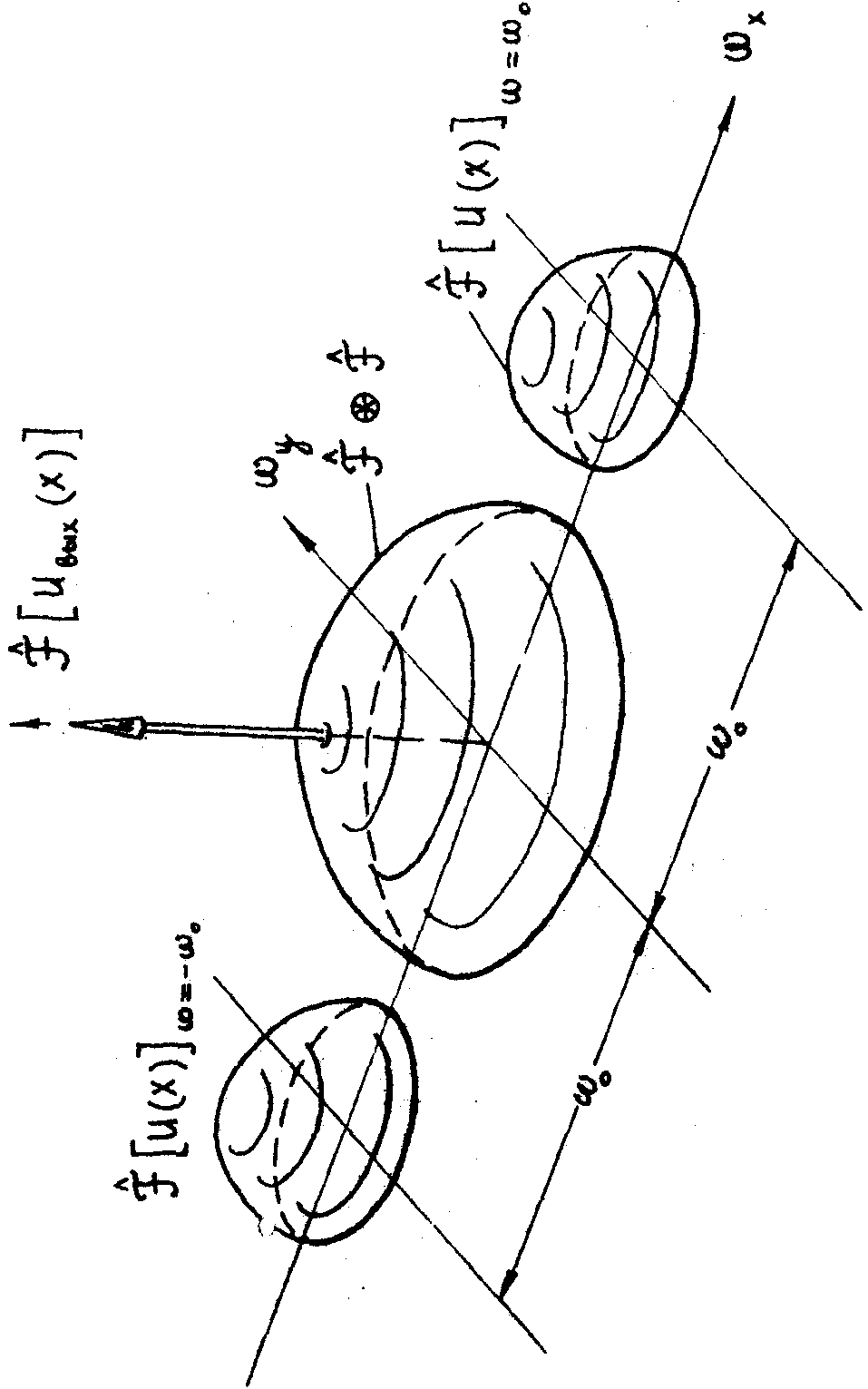
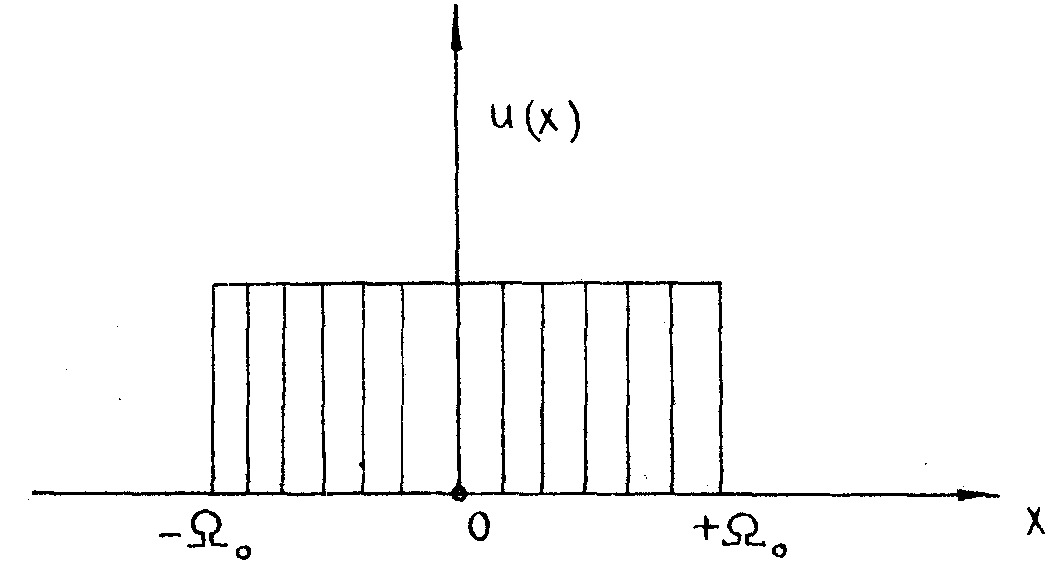
Рис.3. Спектр одномерной действительной функции U(x), рассмотренной нами в качестве примера.
Эта информация действительно останется неискажённой, если вредная автокорреляция не перекрывается с боковыми полосами. Возникает очевидное требование на наинизшее значение несущей
2W
0 + W
0 £
w
0min или w
0min ³
3W
0 (5)
а наивысшая пространственная частота, присутствующая на голограмме, ограничена неравенством:
w
max = w
0 + W
0 ³
4W
0 (6)
Таким образом, пространственная частота, которая должна быть зарегистрирована на голограмме без искажения, по крайней мере в 4 раза больше пространственной частоты, присутствующей в волновом поле u(x). Напомним, что речь идёт здесь именно о волновом поле u(x) в плоскости голограммы, которое сложным образом связано с исходный транспарантом t(x
) или объёмным предметом.
Такова цена, которая платится за то, что в голограмме регистрируется две независимые функции: амплитуда и фаза. Дополнительный множитель 2 возникает из-за того, что фотоэмульсия является детектором, квадратичным относительно амплитуды волнового поля.
Следует подчеркнуть, что интерференционная картина, которая несёт информацию об амплитуде и фазе волнового поля, является неподвижной в пространстве. Это лишь простейший вид голограммы. В общей случае эта интерференционная картина может перемещаться в пространстве с некоторой постоянной скоростью. Устойчивая интерференционная картина с высоким контрастом бежит относительно детектора. Обычной фотоэмульсией такую голограмму зарегистрировать нельзя. Требуются либо стробоскопические методы, либо средства временной развёртки. Важно подчеркнуть, что метод развертки с использованием временных степеней свободы волнового поля может оказаться весьма полезным при быстрой передаче голограммы по каналам связи. Самым важным следствием использования временных степеней свободы волнового поля является то, что устраняется нежелательное увеличение разрешающей способности в 4 раза и, таким образом сохраняется неизменным исходное требование к разрешающей способности. В научных журналах появились лишь первые сообщения на эту тему, и ещё рано говорить о каких-либо технических результатах. Вместе с тем здесь возникает естественный вопрос о том, можно ли с помощью временных степеней свободы волнового поля дополнительно уменьшить требование к разрешающей способности и таким образом получить новую степень свободы в выборе технических параметров системы. Для решения этого вопроса требуются дополнительные теоретические исследования.
Итак, мы рассмотрели простейший случай, когда Фурье-образ поля u(х) имеет вид прямоугольного импульса. Если же поле u(х) произвольно, то все выводы сохраняются, если под W
0 понимать наивысшую пространственную частоту оптического сигнала U(x).
Все рассмотренное выше относилось к идеальному случаю, когда условия экспонирования и проявления фотоэмульсии таковы, что амплитудное пропускание полученной голограммы пропорционально функции распределения интенсивности суммарного волнового поля на голограмме. В действительности такой идеальный случай никогда не реализуется. Однако, если рассмотреть реальные условия экспонирования и проявления, то полученный вывод остаётся в силе. Поясним это, не выписывая формул.
Идеальный случай, который был рассмотрен выше, отвечает степени контрастности Габора, равной g
опт = -2. Обычно проявление ведётся так, что получают негатив: g
¹
-2 и при этом g
>0, то есть степень контрастности имеет противоположный знак. В этом случае приходится прибегать к экспериментальным ухищрениям. Одно из них состоит в том, что используют лишь небольшой участок характеристической кривой фотоэмульсии, и для этого интенсивность опорного пучка выбирают гораздо больше интенсивности предметного пучка. Но каково бы ни было соотношение между интенсивностями опорного и предметного пучков, условие Габора всё равно оказывается нарушенным, и на стадии восстановления всегда возникают пучки второго и более высокого порядка дифракции. При этом пучки второго порядка дифракции не дают правильного отражения исходного волнового поля u(х) потому, что в пучке второго порядка восстанавливается не сама функция u(x), а её некоторые квадратичные комбинации типа uu*, т.е. функции, нелинейным образом связанные с интересующей нас функцией. Эти искажённые пучки не должны мешать качественному восстановлению волнового поля. Наиболее очевидный путь заключается в устранении наложения пучка дифракции первого порядка с его обертонами. Пучок дифракции второго порядка занимает полосу пространственных частот, равную 4W
0, вдвое больше исходной полосы из-за нелинейных искажений, и сосредоточен вблизи точки w
=2w
0. Легко видеть, что наложения отсутствуют, если 2w
0-w
0 ³
W
0-2W
0, т.е. если w
0³
3W
0. Таким образом, возникает такое же требование на несущую пространственную частоту, как и в идеальном случае, g
опт = -2.
Существует один частный случай, когда вредная автокорреляция отсутствует. Поле u(х) должно характеризоваться только одной фазовой функцией при постоянной амплитуде
u(x) = a0exp[ij
(x)] (7)
тогда
uu* = а02 = const (8)
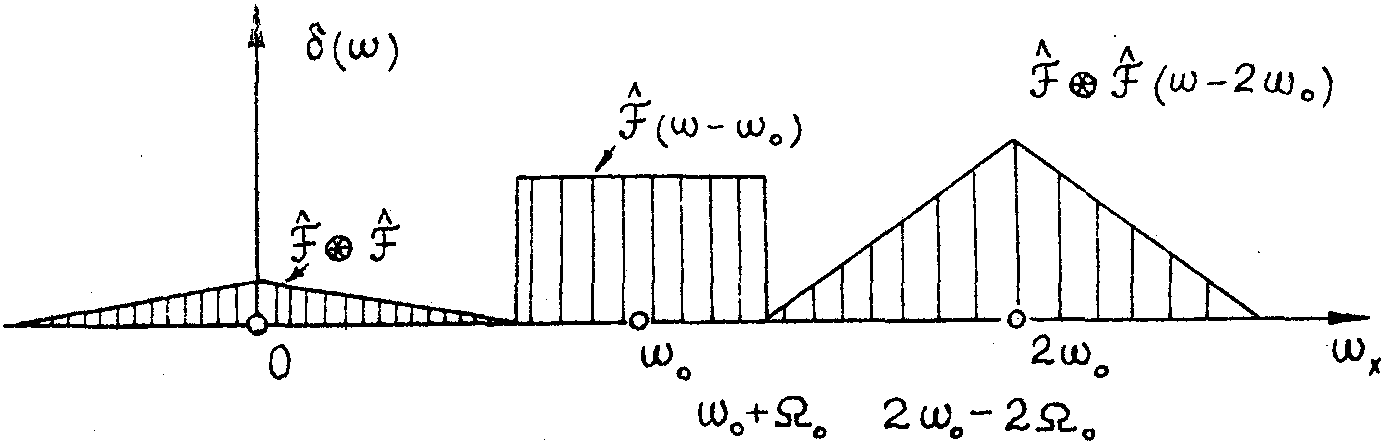
Рис.5. Фурье-образ функции uвых(x) при малой интенсивности предметного пучка по сравнению с опорным пучком.
и слагаемое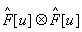 заполнит
только нулевую пространственную частоту. В данном частном случае, если при этом
g опт
= -2, значение несущей пространственной
частоты w 0
можно взять лишь на немного больше частоты
W 0.
К сожалению, случай
(7) очень редко осуществляется в реальных
условиях, особенно в задачах оптической фильтрации.
заполнит
только нулевую пространственную частоту. В данном частном случае, если при этом
g опт
= -2, значение несущей пространственной
частоты w 0
можно взять лишь на немного больше частоты
W 0.
К сожалению, случай
(7) очень редко осуществляется в реальных
условиях, особенно в задачах оптической фильтрации.
Проанализируем теперь структуру волнового поля u(х) в случае голограммы Фурье. Разберём этот вопрос, не выписывая формул, с помощью мысленных экспериментов.
Рассмотрим принципиальную схему получения голограммы Фурье с использованием линзы. В таком виде её не следует осуществлять в реальной экспериментальной установке, так как имеются схемы, которые более эффективны и удобны в работе и не страдают большими аберрациями.
Симметричная тонкая линза Л осуществляет преобразование функции t(x
), представленной в плоскости x
в виде транспаранта, в её Фурье-образ Т(х) на плоскости х, здесь ¦
- фокусное расстояние линзы Л.
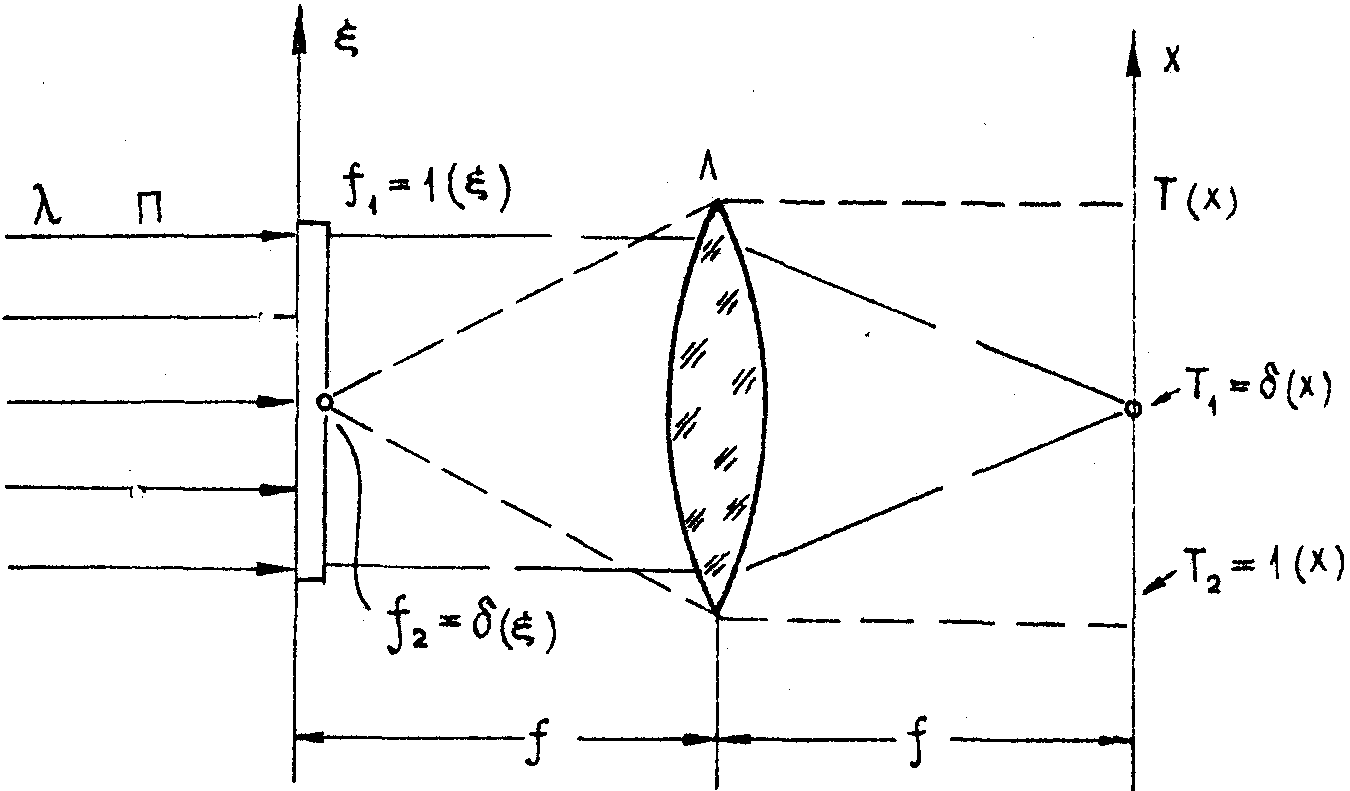
Рис.6. Схема получения Фурье-образа функции t(x
) с помощью собирающей линзы L
.
Случай 1: ¦
1 = 1(x
) полное пропускание;
случай 2: ¦
2 = d
(x
) точечный прокол в непрозрачном экране.
Рассмотрим простейшие иллюстрации. Плоский пучок преобразуется линзой в яркую точку, соответствующей d
-функции на плоскости. Наоборот, если в плоскости x
имеется булавочный прокол, т.е. d
-функция, то линза преобразует её в плоскую волну постоянной фазы, если прокол сделан на оптической оси, и переменной фазы, если прокол сделан вне оси.
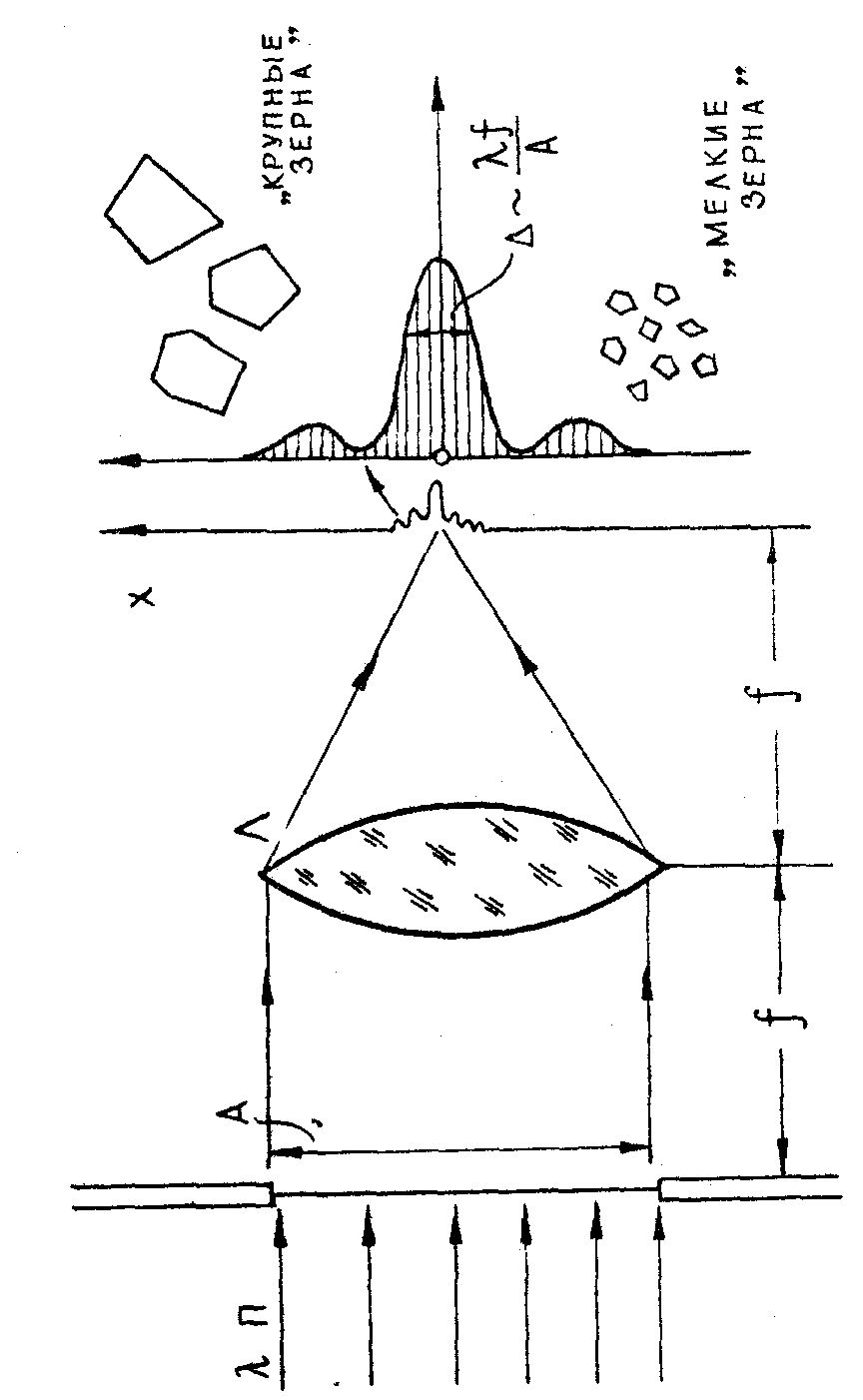
Усложним постепенно мысленные эксперименты. Возьмём теперь плоский пучок, ограниченный апертурой конечных размеров А. Вместо d
-функции в плоскости х появится дифракционное пятно конечных размеров. Уменьшение размера А сопровождается увеличением размера дифракционного пятна. Отметим первую закономерность: чем больше размер апертуры А, тем труднее зарегистрировать детали дифракционного
пятна, которое образуется в плоскости х. В самом худшем варианте, когда фотоэмульсия настолько груба, что не может в деталях зарегистрировать картину дифракционного пятна, на фотопластинке получится пятно увеличенных размеров. Потеря информации, которая при этом происходит, отразится определённым образом на стадии восстановления: наблюдатель увидит только небольшую центральную часть кадра, а края его окажутся тёмными. Таким образом, недостаточная разрешающая способность фотоэмульсии сказывается не на разрешении по предмету, а в уменьшении размеров видимой части кадра. Иначе говоря, требования к разрешающей способности фотоэмульсии в схеме получения голограммы Фурье возрастают по мере увеличения размеров кадра.
Теперь возьмём два близко расположенных прокола в тёмном экране. В плоскости Фурье когерентный пучок, пройдя через эти два прокола, превратится за линзой L
в два плоских наклонных пучка: наклон их тем больше, чем дальше от оптической оси сделан прокол. При интерференции двух плоских волновых фронтов возникнет поле с косинусоидальной амплитудой. Если расстояние между проколами мало, то интерференционная картина имеет очень большой шаг и легко регистрируется. Однако по мере увеличения расстояния между проколами угол между плоскими волновыми фронтами растёт и уменьшается шаг между полосами интерференционной картины. Одновременно с этим возрастает требование к разрешающей способности фотоэмульсии. Итак, близкие два прокола зарегистрировать в плоскости Фурье проще, чем два прокола, отстоящие друг от друга на большом расстоянии. Правда, существует также и иное ограничение, когда шаг интерференционной картины становится настолько большим, что на конечных размерах голограммы не сможет уместиться даже одна полоса. Тогда оба прокола сольются в одно общее пятно. Таким образом, разрешение в предметной плоскости зависит не от разрешающей способности фотоэмульсии, предназначенной для получения голограммы Фурье, а от размеров получающейся голограммы: для лучшего разрешения требуются большие размеры голограммы.
Для подтверждения своеобразного взаимообратного соотношения между размером предмета (или размером голограммы) и пространственным
разрешением по предмету (или разрешающей способности фотоэмульсии) разберём еще один мысленный эксперимент. Вместо точечных проколов в экране возьмём теперь идеальную дифракционную решётку, создающую только пучки дифракции первого порядка. В пространстве перед линзой возникнет два плоских фронта, каждый из которых линза преобразует в точку. Всего в плоскости х возникнет три дифракционных пятна. Поэтому для отображения дифракционной решётки в плоскости Фурье нам потребуется всего лишь три фотографических зерна или три светлых точки, если фотоэмульсию проявить с обращением. Чем меньше шаг дифракционной решётки, тем больше расстояние между этими пятнами. Изменение пространственной частоты решётки никак не проявляется на размере и форме пятна.
Вывод: разрешение по предмету определяется размером голограммы или фотопластинки, а требование к разрешающей способности фотоэмульсии определяется размером предмета-транспаранта.
До сих пор мы говорили лишь о структуре волнового поля, которое существует в плоскости Фурье, и пока не вводили опорный пучок для получения голограммы. Перейдём теперь непосредственно к рассмотрению схемы получения голограммы Фурье на примере двух узких щелей в экране.
Пусть расстояние между этими щелями, расположенными симметрично
относительно оптической оси, равно 2а.
Тогда угол между двумя плоскими волнами
за линзой Л равен 2q
=2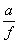 (рис.7),
где
¦ - фокусное
расстояние линзы. В плоскости х возникнет волновое поле
(рис.7),
где
¦ - фокусное
расстояние линзы. В плоскости х возникнет волновое поле
u = ux + u- = exp[ixW
0] + exp[-ixW
0] = 2cosxW
0 (9)
где
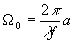 (10)
(10)
Это волновое поле регистрируется на голограмме. Вводится плоский опорный пучок. Поскольку W
0 - единственная и наивысшая пространственная частота волнового поля u(х) и амплитуда этого поля не равна тождественно постоянной величине, то к этому случаю следует применить общий рецепт, сформулированный выше для наиболее
общего вида волнового поля u(х), а именно: частоту пространственной несущей w
0 следует выбрать не меньше 3W
0, w
0 ³
3W
0.
Полное волновое поле в плоскости х, которое регистрируется на голограмме, описывается оптическим сигналом
F(x)=exp[iw
0x]+a
(exp[iW
0x]+exp[-iW
0x]) (11)
Интенсивность, регистрируемая на голограмме, равна
t (x)=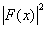 =(1+2a
2)+
=(1+2a
2)+
+a
(exp[iW
0x]+exp[-iW
0x])exp[iw
0x]+
+a
(exp[-iW
0x]+exp[iW
0x])exp[-iw
0x]+
+a
2exp[i2W
0x]+a
2exp[-i2W
0x] (12)
При освещении голограммы t
(х) плоской волной 1(х) возникает волновое поле,
Uвых(x)=t
(x)1(x)=t
(x)
Линза Л на стадии восстановления осуществит обратное преобразование Фурье (рис.8), и в плоскости x
образуется восстановленное изображение с амплитудой,
tвост(x
)=(1+2a
2)d
(x
)+
+a
d
(x
-b-B)+a
d
(x
+b-B)+ (13)
- 88 -
+a
d
(x
-b+B)+a
d
(x
+b+B)+
+a
2d
(x
+2b)+a
2d
(x
-2b) (15)
Первая строчка описывает изображение прямого опорного пучка на стадии восстановления. Вторая строчка ответственна за одно из изображений двух щелей. Третья строчка описывает еще одно изображение двух щелей - по другую сторону от опорного пучка. Наконец, последние две строчки - это лишние изображения щелей, расположенные в точках x
+=2b и x
-=-2b и имеющие смысл автокорреляции двух щелей. Амплитуда волны, создающей изображение этих щелей, в a
раз меньше амплитуды волн полезных изображений (рис.9). Из рис.9 видно, что кадр останется абсолютно чистым только в том случае, если в него не попадут ложные изображения щелей. Этого не произойдёт, если выполнено условие
B ³
3b или w
0 ³
3W
0
Так, на примере пространственного предмета, состоящего из двух узких щелей, можно убедиться в справедливости общего правила о выборе наинизшего значения несущей пространственной частоты в голограмме. В этом примере расстояние между щелями эквивалентно размеру кадра или предмета. Увеличение размера кадра приводит к более высоким пространственным частотам картины интерференции на голограмме.
На стадии восстановления голограммы Фурье было получено два изображения, расположенных симметрично относительно изображения спорного пучка. Совершенно нет смысла спрашивать о том, какое из них мнимое и какое действительное, поскольку представление Фурье имеет смысл представления направления лучей, когда информация передаётся параллельными пучками, и различие между сходящимся пучком,
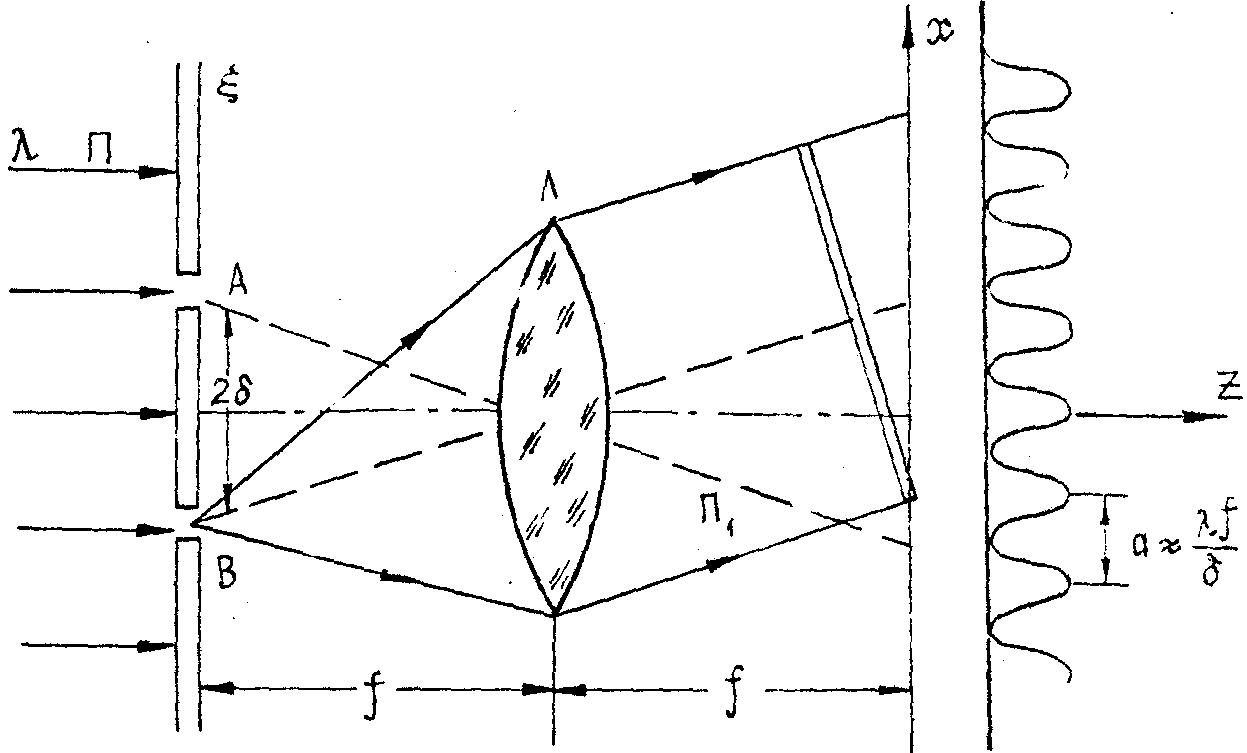
Рис.8. Лучи света от двух точечных проколов А и В преобразуются линзой L
в две плоские волны, которые, и интерферируя, создают косинусоидальное распределение интенсивности в плоскости х. Период косинусоиды "а" обратнопропорционален расстоянию между проколами б.
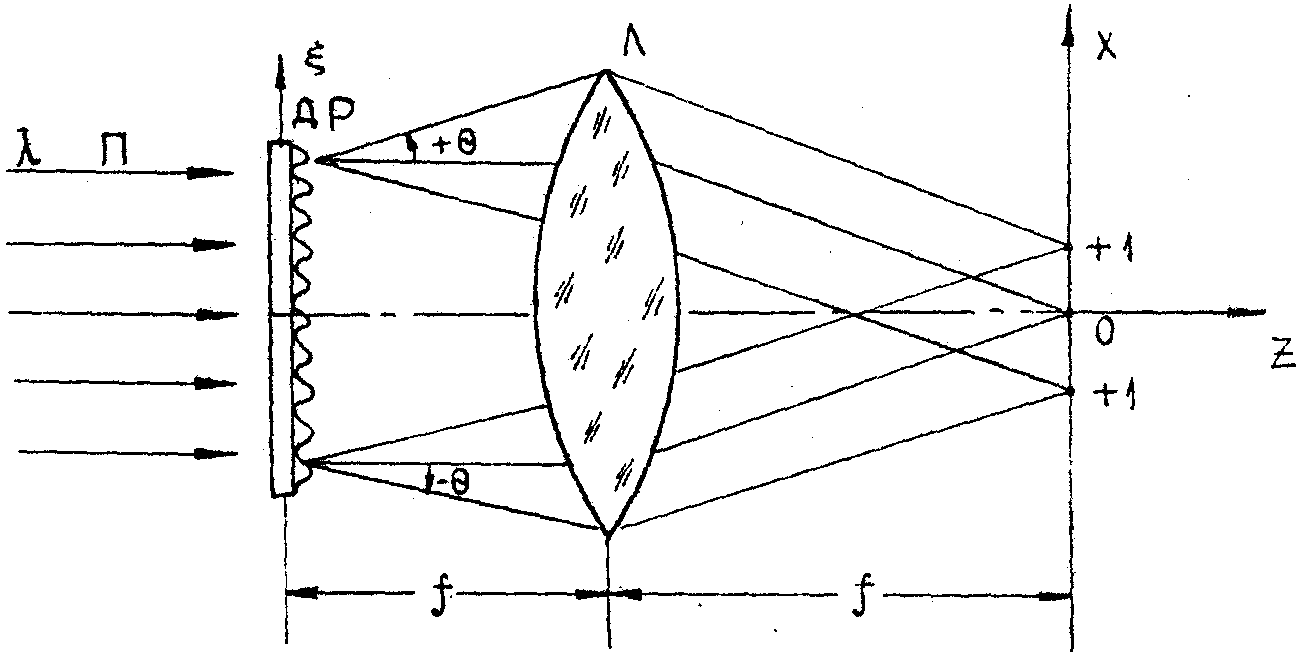
Рис.9. Линза L
фокусирует пучок нулевого и два пучка дифракции первого порядка в три пятна +1, 0 и -1, размеры которых определяются размером участка дифракционной решётки ДР, освещаемой пучком П.
образующим действительное изображение, и расходящимся пучком, ответственным за мнимое изображение, полностью исчезает.
Теперь об обобщённых голограммах.
В лекции С.М.Рытова был разобран общий случай двух предметов (наблюдаемого и опорного) и схема получения голограммы. В плоскости голограммы возникло два волновых поля: одно от наблюдаемого предмета и другое от опорного. При рассмотрении общей схемы голографии было введено упрощающее предположение о том, что волновое поле опорного предмета имеет в плоскости голограммы простейшую структуру, в частности, однородно по интенсивности. Если же это не так, то на стадии восстановления возникают искажения, для устранения которых необходимо осуществить определённую пространственную фильтрацию поля.
Выше было указано, что голограмма позволяет полно и обратимо зарегистрировать волновое поле по амплитуде и фазе. Вторая половина этого утверждения относится только к случаю, когда опорный пучок имеет простейшую структуру, например, если использовать однородный плоский или изотропный расходящийся или сходящийся пучки. Тогда стадия восстановления происходит без каких-либо осложнений, и восстановленное изображение появляется как бы автоматически.
В общем же случае волновое поле от опорного предмета имеет сложную неоднородную структуру, и для таких голограмм, которые можно назвать обобщёнными голограммами, подлинной обратимости нет.
Голографический метод и приём фильтрации на стадии восстановления для обобщённых голограмм можно ввести следующим образом.
Рассмотрим произвольное волновое поле ¦
(x), которое регистрируется, как обычно, фотоэмульсией. При этом фотоэмульсия отобразит распределение интенсивности,
I(x)=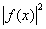 (14)
(14)
и ничего больше: фаза волнового поля ¦
(х) будет полностью потеряна. Представим теперь, что дополнительное опорное волновое
поле мы ввести не можем по каким-то причинам. Как же извлечь информацию о фазе волнового поля ¦
(х)?
В самом общем виде задача решения не имеет. Если нельзя ввести опорного пучка, то информация о фазе полностью ускользает и вместе с ней исчезает информация о дальности до различных точек предмета, т.е. мы полностью лишаемся возможности отобразить третье измерение. Однако существует определённый класс предметов и функций ¦
(х) в плоскости голограммы, для которых можно получить обобщённую голограмму. Предположим, что в неизвестном предмете мы можем выделить некоторую известную часть, расположенную определённым образом относительно её остальной части. Тогда и волновое поле в плоскости голограммы можно представить в виде суммы известной и неизвестной части,
u(x)=uA(x)+u0(x) (15)
где u0 - известная часть. Картина распределения интенсивности,
I(x)=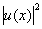 =
=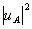 +
+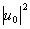 +uA*u0+uAu0* (16)
+uA*u0+uAu0* (16)
включает в себя интерференционную картину, описываемую третьим и четвёртым слагаемыми. Очевидно, что в этой интерференционной картине содержится вся информация о фазе ФА(х) волнового поля неизвестной части предмета. Задача состоит в том, чтобы извлечь эту информацию без каких-либо искажений. Для того, чтобы решить такую задачу, воспользуемся фундаментальным свойством голографического метода - возможностью выполнения апостериорной обработки информации, зарегистрированной голографически. Эта процедура требуется для того, чтобы устранить искажения пространственной структуры голограммы, содержащей в себе картину интенсивности I(х).
Апостериорная процедура устранения искажений сводится к операции деления амплитудного пропускания голограммы (16) на оптический сигнал u0*. Тогда последнее слагаемое в (16) превратится в искомое волновое поле uA(х). Подобную операцию деления выполнить непосредственно нельзя, если только не свести её к двум операциям умножения. Для этого умножим числитель и знаменатель на u0. Тогда
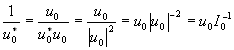 (17)
(17)
Эта операции умножения осуществляются следующим образом. Сначала изготавливают голографический фильтр, осуществляющий умножение на функцию u0. Выполняется эксперимент с получением обычной голограммы от известной части предмета, создающей волновое поле u0. Если использовать в этом опыте плоский опорный пучок, то интенсивность, регистрируемая на вспомогательной голограмме, равняется
I1(x)=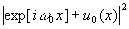 =1+
=1+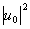 +u0*exp[iw
0x]+u0exp[-iw 0x](18)
+u0*exp[iw
0x]+u0exp[-iw 0x](18)
При определённом проявлении голограммы её амплитудное пропускание равно
t1(x)=I1(x) (19)
Последнее слагаемое в
(18), создающее на стадии восстановления
пучок, распространявшийся под углом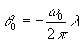 ,
ответственно за операцию умножения на функцию
u0.
,
ответственно за операцию умножения на функцию
u0.
Фильтр для осуществления операции умножения на I0-1(x) изготавливается в другом отдельном эксперименте путём регистрации распределения интенсивности I0(х) на фотопластинке с последующим проявлением её до коэффициента контрастности g
=+2. Амплитудное пропускание получившегося фильтра равно
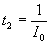 (20)
(20)
Сложив оба фильтра вместе, мы подучим фильтр, амплитудное пропускание
которого в направлении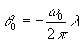 равно
равно
t(x)=t1(x)t2(x)=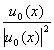 (21)
(21)
Запишем теперь выражение для амплитуды света непосредственно за голограммой, ограничившись рассмотрением только той её части, которая распространяется в направлении,
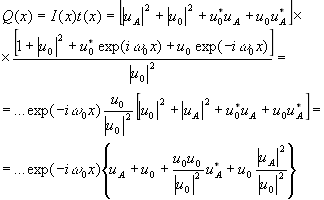 (22)
(22)
Первое слагаемое в фигурных скобках описывает искомое волновое поле uA, а второе - волновое поле от известной части предмета. Третье слагаемое эквивалентно действительному изображению uA*, сильно искажённому дополнительным множителем. Этот множитель характеризуется удвоенным значением фазы, что приводит к сильному размытию волны uA*. Последнее слагаемое соответствует волновому полю известной части предмета, искажённому только по амплитуде. Поэтому соответствующая волна накладывается на волну u0 от второго слагаемого.
Для того, чтобы волновое поле uA* отделялось в пространстве от волнового поля uA, достаточно, чтобы опорный предмет, создающий волну u0, располагался бы в стороне от предмета наблюдения uA или же на другом расстоянии от голограммы Тогда изображение, создаваемое слагаемым
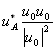
расположится с противоположной стороны от известной части предмета u0.

