|
|
 |
 |

|
| |
- 248 -
преобразование ПРОСТРАНСТВА, ОСУЩЕСТВЛЯЕМое ГолОГРаМмОЙ
Г.И.Косоуров
Излагая основные принципы голографии, чаще всего для простоты рассуждений предполагают, что при восстановлении изображения голограмма занимает то же самое положение, которое занимала светочувствительная поверхность при получении голограммы. При этом одно из двух восстановленных изображений по размерам и положению относительно голограммы и опорного пучка точно соответствует голографируемому предмету. Однако, если при получении голограммы опорный пучок образовался точечным источников света, то при восстановлении изображении появляются при любом положении источника. Изображения будут несколько испорчены аберрациями, которыми во многих случаях можно пренебречь. Положение и масштаб изображений, а также их действительность или мнимость будут зависеть от взаимного расположения голограммы и источника. Кроме того, мы можем воспользоваться копией голограммы с измененным масштабом и изменить длину волны света, и это не помешает получить восстановленное изображение.
Если отвлечься от аберраций и дифракционной структуры изображении и при получении голограммы ввести в пространстве предмета систему координат х, у, z, а при восстановлении изображения в пространстве изображений координаты х', у', z', то можно выразить координаты точек изображения через координаты точек предмета. Соответствующие формулы можно рассматривать как формулы точечного преобразования пространства предмета в пространство изображения, а голограмму вместе с опорным пучком - как своеобразную оптическую систему, осуществляющую это преобразование. Существенно, что характер преобразования зависит только от положения точечных источников при записи и восстановлении голограммы и изменения масштабов голограммы и длины волны и никак
- 249 -
не зависит от голографируемого предмета.
Формулы голографического преобразования пространства и условия получения безаберрационного изображения широкими пучками лучей имеют много общего с формулами обычных линз и зеркал геометрической оптики. Для лучшего понимания закономерностей трансформации голографического изображения при изменении геометрии опорного пучка полезно сопоставить хорошо знакомые понятия и формулы геометрической оптики с формулами голографии.
Основным понятием геометрической оптики является понятие луча, прямолинейного в однородной среде и изменяющего направление на границе раздела сред по законам отражения и преломления. Волновая природа света вскрывает ограниченность понятия луча. Строго говоря, задачу об отражении и преломлении ограниченной волны на границе раздела сред следует рассматривать как дифракционную задачу, однако в большинстве случаев, когда речь идёт об определении положения точек изображения и во многих задачах определения аберраций, геометрическая оптика даёт результаты, практически совпадающие со строгим дифракционным решением.
Если рассматривать элементы голограммы, содержащие достаточно много максимумов и минимумов пропускания или изменения фазы, но настолько малые, что направления прямых, проведённых из всех точек элемента в точку предмета или изображения, можно считать одинаковыми, то дифрагированную на таком элементе волну можно достаточно точно характеризовать "дифрагированным" лучом, вышедшим из средней точки этого элемента. Естественно, что лучевые представления мало подходят для выяснения физических принципов голографии - явления существенно волнового, но если физические принципы голографии можно считать выясненными, то для нахождения положения точек голографического изображения вполне уместно пользоваться понятием луча и использовать весь аппарат геометрических построений обычной оптики. Для этого только необходимо сформулировать правила, по которым можно находить направление дифрагированного луча, заменяющее законы преломления и отражения. Конечно, положение голографического изображения может быть
- 250 -
найдено и из интегрального соотношения, определяющего световое поле в пространстве за голограммой, а лучи рассматривать как вспомогательные понятия, не заботясь об их физическом смысле, однако мы не будем очень щепетильны, вводя для наших целей понятие луча в голографию.
4. Точечное линейное преобразование пространства
Идеальная оптическая система так же, как и идеальная голограмма, устанавливает между точками пространства предмета и точками пространства изображения взаимно-однозначное соответствие, причём прямые пространства предмета переходят в сопряжённые или прямые пространства изображения, а точке пересечения прямых сопряжена точка пересечения их изображений.
Хорошо известно, что единственным преобразованием с такими свойствами является линейное или проективное преобразование пространства, формулы которого при произвольном выборе прямоугольных декартовых координат х, у, z в пространстве предмета и х', у', z' в пространстве изображения имеют вид:
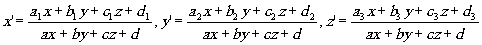 (1) (1)
Формулы обратного преобразования имеют аналогичный вид:
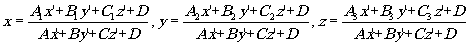 (1) (1)
где А , В и т.д. выражаются через детерминанты, составленные из a, b и т.д.
Легко видеть, что при прямом и при обратном преобразованиях плоскости переходят в плоскости. Плоскость
а x+by+cz+d = о
обращая в нуль знаменатель (1), даёт x'→¥
, y'→¥
, z'→¥
, т.е. отображается на бесконечно удалённую плоскость пространства изображения. Её, как известно, называют фокальной плоскостью
- 251 -
пространства предмета. Аналогично фокальная плоскость пространства изображения имеет уравнение
Ах'+ By'+Cz'+D = 0
система параллельных плоскостей, имеющих общую бесконечно удалённую прямую, отображается на пучок плоскостей, имеющих общую прямую на фокальной плоскости соответствующего пространства. Только плоскости, параллельные фокальной в пространстве предмета, переходят снова в параллельные плоскости. Они параллельны фокальной плоскости пространства изображения.
Общие формулы (1) и (2) можно упростить, взяв за координатные плоскости х, у и х', у' плоскости, параллельные фокальным. Тогда z' будет зависеть только от z. Поместив начала координатных систем в сопряжённых плоскостях, получим:
z' = с 3z/(cz+d) (5)
Следующий шаг упрощения связан с тем, что в плоскости z=0 существуют два взаимно-перпендикулярных направления, переходящие во взаимно-перпендикулярные направления плоскости z'=0. Примем их за оси х, y и x' и y', взяв за начала координат сопряжённые точки, разделив все коэффициенты на d и выбрав соответствующим образом положительные направления на осях х', y' и z', получим из (1) и (3):
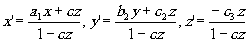 (4) (4)
где все коэффициенты считаются положительными.
Из всех прямых, перпендикулярных к плоскостям z=const, только одна прямая, называемая оптической осью, переходит в прямую, перпендикулярную плоскостям z'=const. Приняв её за ось z, а ее изображение за ось z', получим:
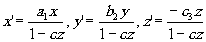 (4) (4)
- 252 -
Координаты х 0, у0 и х'0, у'0 оптической оси в старых координатах можно найти из формулы (4) и условия, что новые координаты дают формулы (5). Легко получить, что
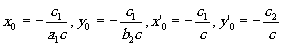 (6) (6)
Если система имеет ось симметрии, то оптическая ось совпадает с ней и b2=а1. Мы ограничимся рассмотрением этого случая и будем писать соотношения только для x и z.
Теперь можно найти пояснение кардинальных: плоскостей.
Фокальные плоскости:
Z'→¥
, zF = 1/c и Z→¥
, z'F = c3/c (7)
Главные плоскости, для которых увеличение равно единице:
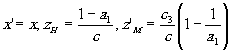 (8) (8)
Расстояния между фокальными и главными плоскостями называют фокусными расстояниями системы. Из (7) и (8) найдём
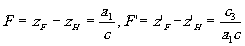 (9) (9)
Отношение F'/F в обычной оптике равно относительному коэффициенту преломления пространства изображения
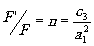 (10) (10)
Зная положение кардинальных плоскостей, легко построить изображение любой точки по известным игольным правилам. Обычно начала координат помещают в главные плоскости. Тогда (5) перейдёт в
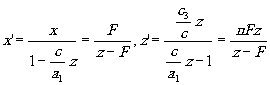 (11) (11)
- 253 -
Величину 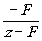 называют поперечным увеличением системы, а формулу для z'
можно представить в виде привычной формулы линзы:
называют поперечным увеличением системы, а формулу для z'
можно представить в виде привычной формулы линзы:
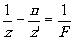 (12) (12)
Таким образом, мы видим, что известные из оптики формулы преобразования пространства не являются специфическими для линз и зеркал, а обязательны для преобразования любой физической природы в тех областях пространства, где они претендуют на взаимооднозначность и точечность с сочетанием прямолинейности. Это могут быть прямолинейные траектории электронов в электронной оптике, траектории ионов и т.д. Общий характер преобразования в смысле взаимного разделения пар сопряжённых точек сохраняется даже для криволинейных траекторий. Заметим, что формулы линз были заново "открыты" экспериментально в 30-е годы в электронной оптике. Эти же формулы обязательны и для голографии в той степени, в какой голография даёт свободное от аберраций восстановленное изображение .
Выведем из (11) одно следствие. Возьмём две сопряжённые точки x,z и z',x' по (11)
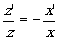
Рассмотрим сопряжённые лучи, выходящие из точек пересечения оси с плоскостями, содержащими взятые точки (рис.1). Легко видеть, что
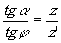
откуда
nx'tdj
' = -xtgj
(13)
Таким образом, углы, которые составляют сопряжённые лучи с осью, связаны с увеличением в плоскостях, проходящих через точки пересечения лучей с осью, условием тангенсов (13). Условию тангенсов можно придать более общий вид.
Рассмотрим снова две сопряжённые точки х ,z и х',z' и две любые пары проходящих через них сопряжённых лучей, образующих с осью углы j
1, j
2 и j
'1,j
'2 (рис.2). Выражая тангенсы этих
- 254 -
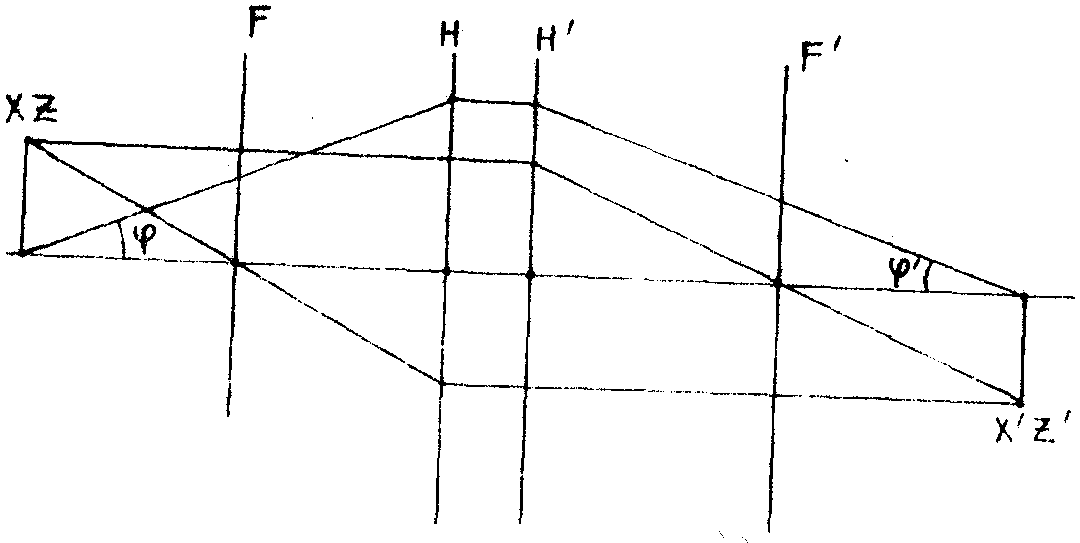
Рис.1.
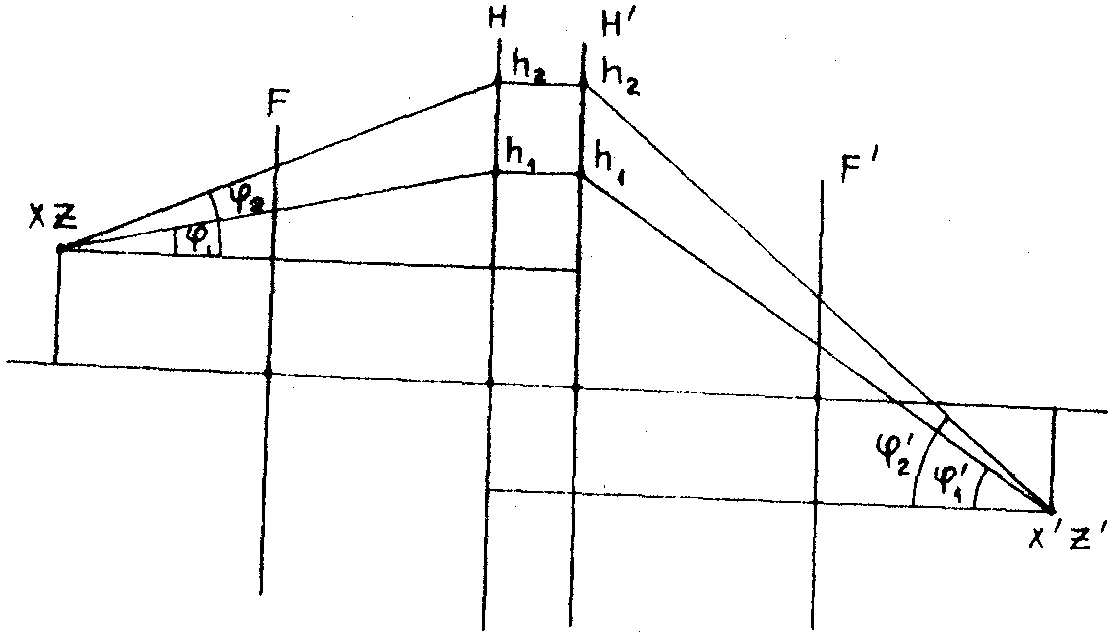
Рис.2.
- 255 -
углов черва х ,z и x',z' и высоты h1 и h2, на которых лучи пересекают главные плоскости, и учитывая (11), найдём
tgj
1-tgj
2 = nm(tgj
'1-tgj
'2) (14)
где m - увеличение в плоскостях, содержащих выбранные точки.
2. Геометрическая оптика
Пока мы рассматриваем пространство предмета м пространство изображения независимо, всегда можно выбором направлений осей координат привести формулы преобразования к виду (11) с положительными коэффициентами, при котором в обоих пространствах фокальные плоскости лежат на положительных полуосях z и z'. В оптике пространства предмета и изображения связаны между собой оптической системой, и можно все системы разделить на два класса. В первом классе отражательных или катоптрических систем положительные направления осей z и z' совпадают и фокусы лежат по одну сторону оптической системы как у сферического зеркала. Во втором, диоптрическом классе направления осей z и z' противоположны и фокальные плоскости лежат по разные стороны оптической системы как у линзы. На формулах преобразования это никак не сказывается и по их виду мы не можем сказать, с какой системой имеем дело.
Другая особенность оптики, отличающая её от геометрии, связана с тем, что лучи, в противоположность прямым геометрии, имеют направление распространения. Так как изображение может образовываться пересечением лучей только после прохождения через оптическую систему, то приходится различать действительные и мнимые изображения и действительные и мнимые источники, хотя с точки зрения геометрии они совершенно эквивалентны. Каждый выделенный нами класс оптических систем разделяется ещё на два типа систем. собирающих, как выпуклая линза и вогнутое зеркало. и рассеивающие, как вогнутая линза и выпуклое зеркало. При нашем способе выбора направлений осей z и z' мы должны были бы считать координаты
- 256 -
точек источника перед рассеивающей линзой и координаты точек изображения за линзой отрицательными. Однако в оптике принято другое правило знаков. Направление осей выбирают так, чтобы действительные изображения и источники имели положительные координаты. Тогда рассеивающие системы будут иметь отрицательные или мнимые фокусы. Подчеркнём ещё раз, что если бы направление луча в оптике было бы безразлично, то изображение в рассеивающей линзе перед линзой физически ничем не отличалось бы от изображении за собирающей линзой.
В оптических системах всегда оба фокуса либо положительны, либо отрицательны. Системы с фокусами разных знаков не могут быть осуществлены в оптике, так как мы не можем изменить направление лучей в системе, не поменяв при этом роли пространства предмета и изображения. Последняя обратимость в оптике всегда возможна.
Посмотрим теперь, как оптика справляется с осуществлением проективного преобразования, в частности с выполнением условия тангенсов (13). Волновые свойства света приводят к общему принципу - так называемому принципу Ферма, по которому луч света. между двумя точками распространяется всегда по экстремальному пути. Из этого следует, что оптические длины всех лучей между точкой и её изображением должны быть одинаковыми.
Возьмём две сопряжённые точки на оси оптической системы. Лучу, выходящему из точки предмета под углом j
к оптической оси, сопряжён луч в пространстве изображения, составляющий угол j
' с осью z'. Сместимся из точки предмета в направлении, перпендикулярном к оптической оси, на малую величину х. Точки изображения сместятся на х' (рис.3). Для этих точек так же, как и для исходных, оптические длины путей должны быть одинаковыми для любых лучей. Но оптическая длина пути в пространстве предмета вдоль луча под углом j
уменьшилась на хSinj
, а в пространстве изображения увеличилась на х'Sinj
'. С другой стороны, луч, идущий параллельно оптической оси при малых х и х', не изменил своей длины. Поэтому и вдоль лучей j
, j
' оптическая длина пути не должна измениться. Откуда
- 257 -
nx'Sinj
' = хSinj
(15)
Рис. 3.
Мы получили известное условие синусов. Сравнивая (13) и (15), мы видим, что, в то время как точечность и взаимная однозначность преобразования с сохранением прямолинейности лучей требуют выполнения условия тангенсов (13), физическая природа света приводит, вообще говоря, к несовместимому с ним условию синусов (15). Оптические системы, как правило, не могут давать идеального точечного изображения пространства и обладают аберрациями. Исключение могут составлять случаи, когда оба условия удовлетворяются везде или только в некоторых точках одновременно. То же имеет место и в электронной оптике.
По-видимому, наиболее важным является случай параксиальной оптики, когда углы, составляемые лучами с осью, малы и условия (13) и (15) выполняются одновременно из-за практического совпадения тангенсов и синусов. К этому случаю относятся большинство оптических приборов и все приборы электронной оптики.
Важным случаем являются так называемые апланатические системы, в которых законы геометрической оптики удаётся совместить с выполнением условия синусов для элемента поверхности в окрестности одной точки на оси системы или для пары сопряжённых поверхностей. Апланатические системы изображают без аберраций широким пучком лучей окрестность такой точки. Известный примером апланатической системы является сфера с коэффициентом преломления n и радиусом R. Точки, лежащие на сферах радиусов nR и R/n, изображаются
- 258 -
друг на друга без аберраций. Точки поверхности nR мнимые, т.е. в них пересекаются не лучи, а их продолжения. Апланатические свойства сферы используются при конструировании объективов микроскопов, где существенна большая апертура пучков, а положение предмета может быть фиксировано.
Более глубокое исследование свойств оптических систем на основании принципа Ферма приводит к выводу, что если существуют идеальные оптические системы с однородными средами в пространстве предмета и в пространстве изображений, то в таких системах оптическая длина любой линии на предмете должна быть равна оптической длине её изображения. Это значит, что увеличение для всех точек пространства должно равняться отношению коэффициентов преломления крайних сред.
В оптике известна только одна идеальная оптическая система. Это всем известное плоское зеркало, в котором условие тангенсов и синусов выполняется одновременно в силу равенства углов падения и отражения. Выполняется также и второе условие идеальной системы - равенство увеличения отношению коэффициентов преломления, т.е. единице. В оптике нельзя осуществить плоское зеркало, в котором лучи после отражения попадали бы в среду с другим коэффициентом преломления, поэтому нельзя осуществить идеальную систему с увеличением. Как мы увидим далее, в голографии такие системы возможны.
Существует ещё одна идеальная система, на которую в оптике не обращают внимание в силу её тривиальности, соответствующая тождественному преобразованию. В голографии такое преобразование уже не является тривиальным, тем более, что такое преобразование может быть получено с увеличением так же, как и голографический аналог плоского зеркала.
3, Геометрическая оптика голограмм
Формулы голографического преобразования пространства легко получить, учитывая, что голограмма при восстановлении изображения сопряжена голограмме при ее получении с коэффициентом увеличения m, если применяется увеличенная копия голограммы, а
- 259 -
точечный источник света при восстановлении сопряжён точечному источнику опорной волны. Если при восстановлении длина волны увеличена в m
раз, то, как показывает любое дифракционное явление, это эквивалентно введению в пространстве изображений коэффициента преломления n = 1/m
.
Вводя системы координат, совместим плоскости z=0 и z'=0 с плоскостями голограмм, а начала координат поместим в соответствующие друг другу, значит, и сопряжённые, точки так, чтобы ось z проходила через источник опорной волны. Пусть его координаты будут: х=0, z=z0; координаты источника восстанавливающей волны в пространстве изображений пусть будут: х=х1, z'=z 1. Обращаясь к формулам (4) и (10), найдём:
a1 = m; c3 = m2/m
(16)
Подставляя в ( 4) известные z0, x1 и z1, найдём:
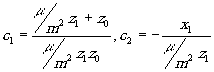 (17) (17)
Тогда формулы преобразования (4) примут вид:
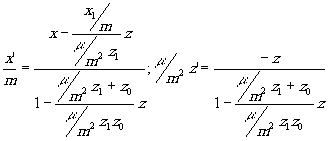 (18) (18)
Положение оптической оси найдём из (6)
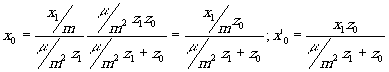 (19) (19)
Обозначая
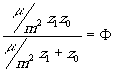 (20) (20)
выразим через F
положение кардинальных плоскостей и фокусные расстояния:
- 260 -
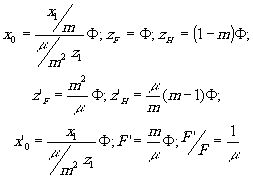 (21) (21)
Формулы (18) примут вид:
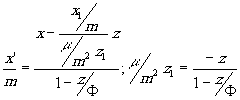 (22) (22)
Совмещая оси z и z' с оптической осью и отсчитывая z и z' от главных плоскостей, получим формулы (11) в виде:
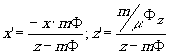 (23) (23)
Расположив голограммы параллельно и совместив оптические оси, будем рассматривать процессы получения и восстановления голограммы как единый процесс преобразования изображения в оптической системе. Как мы уже выяснили в отделе геометрической оптики, возможны две взаимные ориентировки осей z и z'. Если они антипараллельны как в линзе, z' надо считать отрицательными, когда источник восстанавливающего света расположен по ту же сторону голограммы, как и источник опорной волны. В этом случае при m=m
=1, при совмещении источников по (20) F
→¥
и по (22) х'=х и z'=-z мнимое изображение источника совместится с предметом, Поэтому изображение, соответствующее антипараллельным осям, будем называть восстановленным изображением. Голограмма при этом эквивалента линзовой системе. В голографии одновременно осуществляется и второе возможное преобразование с параллельными осями z и z', эквивалентное зеркальной системе. Соответствующее изображение назовём сопряжённым.
- 261 -
Проследим за изменением параметров оптической системы, соответствующей
восстановленному в указанном смысле олова изображению. Пусть
z0 конечно и x1=0.
Начнём со случая, когда
zF
бесконечно и находится по ту же сторону, что и
z0.
По
(21) положение фокуса zF
определяется (20). При
zF=-¥
система эквивалентна собирающей линзовой
системе, фокусы которой расположены в точках zF=z0
и 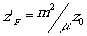 по разные стороны голограмм.
по разные стороны голограмм.
Приближая z
к плоскости голограммы, мы будем отодвигать точки фокусов, уменьшая оптическую
силу эквивалентной собирающей системы. При
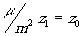 оптическая
сила эквивалентной системы обращается в нуль, а фокусы уходят на бесконечность.
Если m=m
=1, это соответствует точному повторению
условий получения голограммы и мнимое изображение, как мы уже отмечали, совпадёт
с предметом. Если m /m=1
и m ¹
1 (22) даёт: оптическая
сила эквивалентной системы обращается в нуль, а фокусы уходят на бесконечность.
Если m=m
=1, это соответствует точному повторению
условий получения голограммы и мнимое изображение, как мы уже отмечали, совпадёт
с предметом. Если m /m=1
и m ¹
1 (22) даёт:
x' = mx; z' = -mz (24)
Изображение подобно предмету и увеличено в m раз. Из точности воспроизведения условия получения голограммы следует, что изображение будет заведомо идеальным. Этот случай соответствует идеальному тождественному преобразованию в оптике с точностью до увеличения.
Дальнейшему приближению z1
к плоскости голограммы соответствуют отрицательное F
и отрицательные фокусы, сначала далёкие, но быстро приближающиеся к плоскости
голограммы при приближении к ней z1.
Эквивалентная система является рассеивающей
линзой, оптическая сила которой растёт вплоть до бесконечности (фокусы обращаются
в нуль) при совпадении z1
с плоскостью голограммы. Переходя на
другую сторону голограммы, что означает освещение голограммы сходящимся за ней
пучком лучей, z1
становится положительным, а эквивалентная оптическая система снова собирающей.
Ее оптическая сила убывает от бесконечности, когда z1
находится в плоскости голограммы, до значения, с которого мы начали, когда
z1 уходит на
+¥ , а
фокусы возвращаются в точки mz0
и 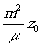 . .
- 262 -
Изменение zF с изменением z1 показано на графике рис.4. Там же обозначены эквивалентные оптические системы.
Если в рассмотренном преобразовании изменить направление лучей,
освещая голограмму с другой стороны, то мы получим систему, строго говоря, не
соответствующую никакой оптической системе, так как в ней действительные и мнимые
изображения поменялись местами по сравнению с линзой. В частности, идеальное
изображение при 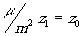 окажется действительный. В оптике ей должна была бы сопоставлена система, у
которой один фокус положительный, а другой отрицательный.
При этом мы сталкиваемся с явлением псевдоскопии,
при котором предметы, более далёкие в смысле перспективы, закрывают предметы
более близкие. Явление
псевдоскопии наблюдается в оптике только в сложных интегральных системах и в
стереоскопах
окажется действительный. В оптике ей должна была бы сопоставлена система, у
которой один фокус положительный, а другой отрицательный.
При этом мы сталкиваемся с явлением псевдоскопии,
при котором предметы, более далёкие в смысле перспективы, закрывают предметы
более близкие. Явление
псевдоскопии наблюдается в оптике только в сложных интегральных системах и в
стереоскопах
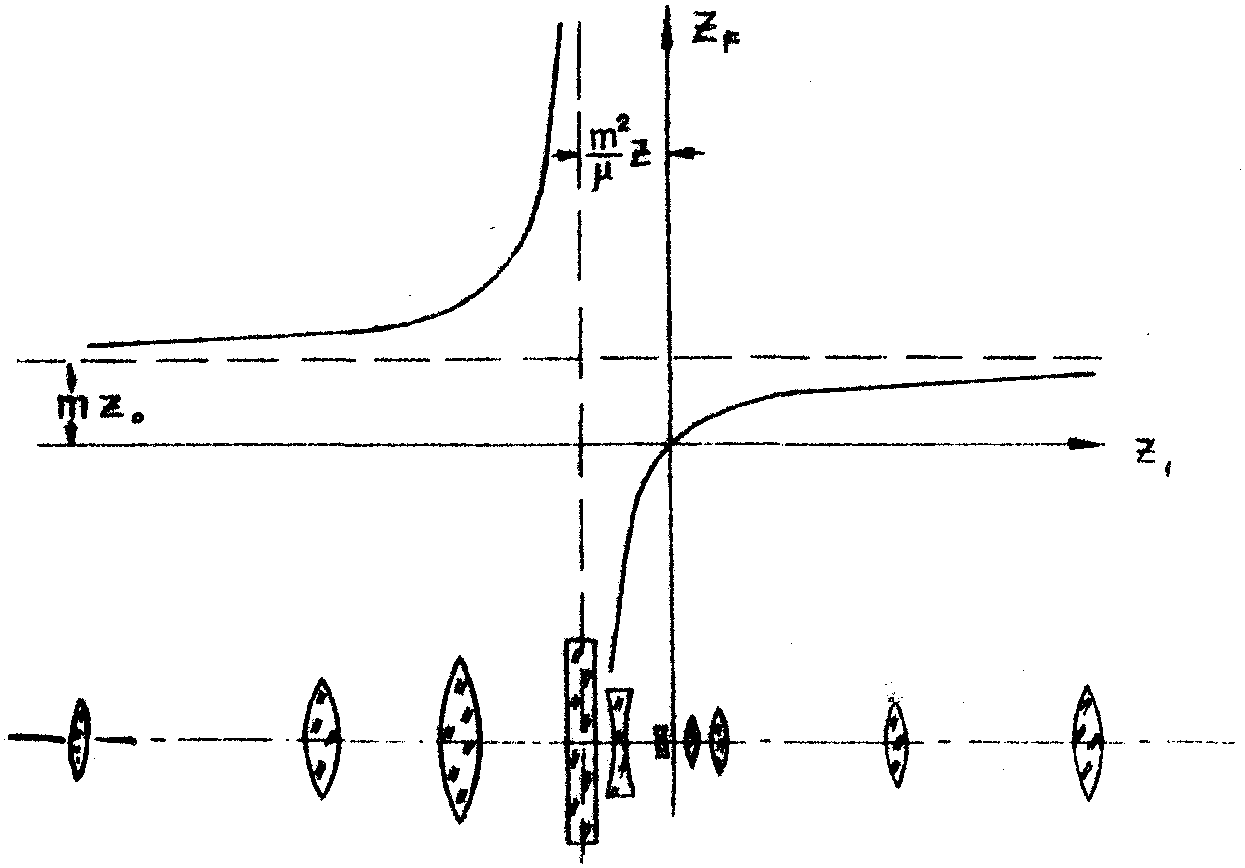
Рис.4 .
- 263 -
при перестановке изображений для правого и левого глаз. Отметим, что все эти системы, как и голографическая, - двухступенчатые. Мы не склонны выделять такие системы в особый класс, так как вид преобразования при этом не меняется и на чертеже: если не сказано направление лучей, они неотличимы. Геометрическое построение изображения точки в них производится так же, как и в обычных системах. Нам представляется более полезным подчеркнуть их аналогию с линзовой системой и отметить отсутствующую у линз возможность обращения хода лучей только в пространстве изображений.
Перейдем к преобразованию, соответствующему сопряженному изображению.
Для того, чтобы получить систему, аналогичную зеркальной, начнём с освещения
голограммы слабосходящимся пучком лучей со стороны, противоположной опорному
пучку. Тогда z1
положительно (оси параллельны) и велико. Если
m=m =1, система
эквивалентна вогнутому зеркалу с фокусом в точке
mz0. В общем случае фокусы
F и
F' находятся в разных точках: z=mz0;
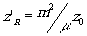 . Это
соответствует гипотетическому в обычной оптике случаю отражения в среду с другим
показателем преломления. . Это
соответствует гипотетическому в обычной оптике случаю отражения в среду с другим
показателем преломления.
Приближение z1
к голограмме приводит к уменьшению фокусных расстояний зеркала вплоть до нуля
при совпадении z1
с плоскостью голограммы. При переходе
z1 через плоскость голограммы
F меняет знак, и наша система становится эквивалентной
выпуклому рассеивающему зеркалу. Когда 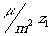 попадает в точку
z0, эквивалентное зеркало
превращается в плоское и даёт мнимое зеркальное изображение предмета. Если
попадает в точку
z0, эквивалентное зеркало
превращается в плоское и даёт мнимое зеркальное изображение предмета. Если 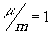 и m ¹
1, то оно идеально и увеличено в
m раз. Дальнейшее перемещение
z1 приводит нас снова к вогнутому
зеркалу, фокус которого уменьшается от бесконечного до mz0,
когда z1 уходит
на бесконечность.
и m ¹
1, то оно идеально и увеличено в
m раз. Дальнейшее перемещение
z1 приводит нас снова к вогнутому
зеркалу, фокус которого уменьшается от бесконечного до mz0,
когда z1 уходит
на бесконечность.
Изменение направления лучей, как и в первом случае, меняет
местами действительное и мнимое изображения и приводит к псевдоскопии. Идеальное
зеркальное изображение при 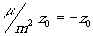 будет при таком ходе лучей действительным.
Ход zF
при изменении z1 приведён
на графике рис.5.
будет при таком ходе лучей действительным.
Ход zF
при изменении z1 приведён
на графике рис.5.
Если x1¹
0, то оптическая ось не будет совпадать с первоначально выбранными осями z и z'. Её координаты будут меняться с
- 264 -
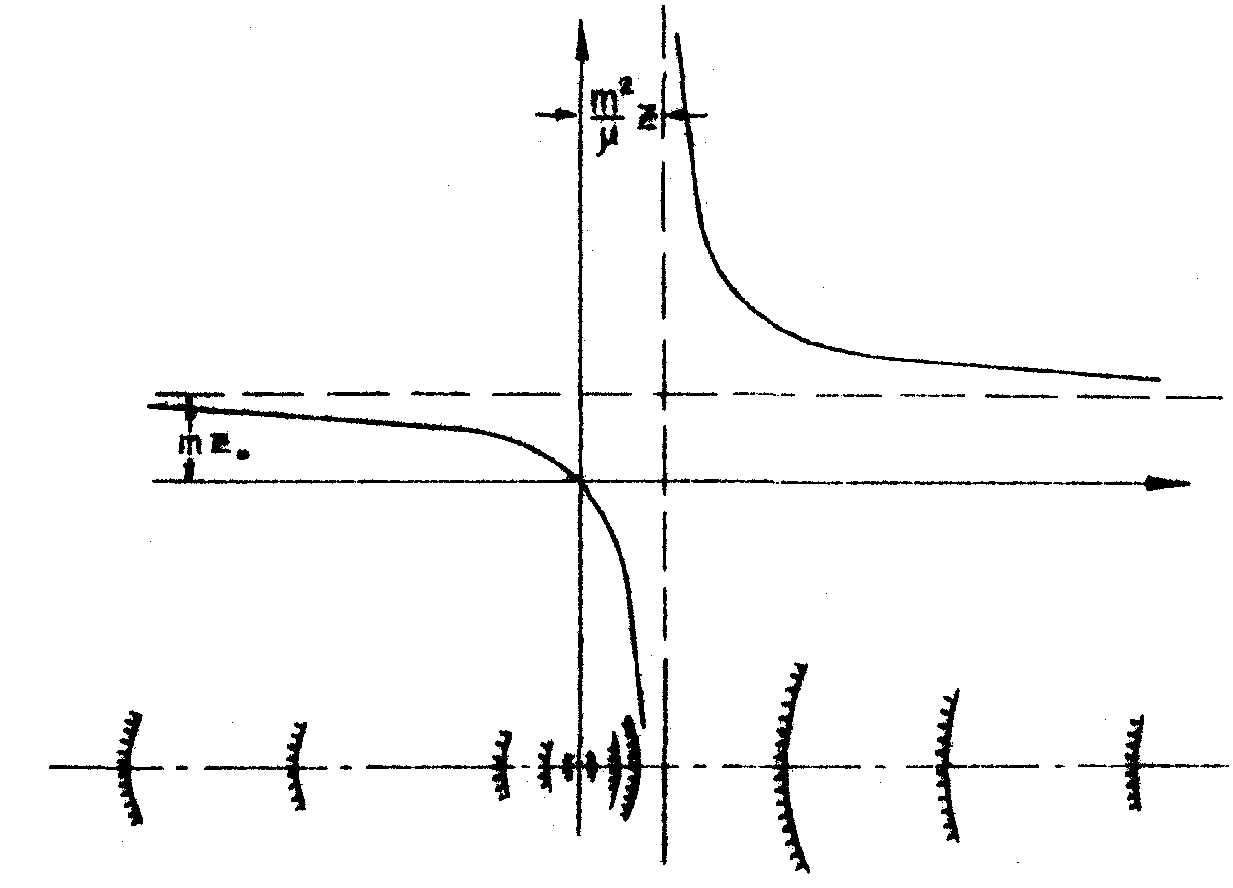
Рис .5 .
изменением z1,
согласно формул (19). Геометрически
положение оптической оси в пространстве изображений x'0
определяется для восстановленного изображения пересечением прямой, проходящей
через точки z0 и
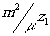 с плоскостью голограммы (рис.6), а для сопряжённого изображения пересечением
прямой, проходящей через точку
с плоскостью голограммы (рис.6), а для сопряжённого изображения пересечением
прямой, проходящей через точку 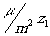 и точку –z0,
зеркально-симметричную с z0
(рис.7).
и точку –z0,
зеркально-симметричную с z0
(рис.7).
Между восстановленным и сопряжённым изображениями точки существует линейное преобразование. Его легко получить, если написать формулы (18) при заданных z0 и z1 для обоих преобразований, считая для сопряжённого преобразования z'1 и z'2 отрицательными. Исключая z, найдём:
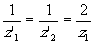 (25) (25)
Оба изображения перспективны относительно точки z, Преобразование от z'1 и z'2 эквивалентно зеркалу с фокусным расстоянием
- 265 -
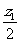 .
Вопрос о действительности или мнимости изображений решается в зависимости от
направления освещения. .
Вопрос о действительности или мнимости изображений решается в зависимости от
направления освещения.
Повторим во избежание недоразумений, что мы исследовали, как меняется характер эквивалентной оптической системы при перемещении голограммы относительно источника света. Сами же голографические изображения при известном z1 и заданном z0 могут быть построены, как изображение голографируемого предмета в такой оптической системе по формулам (18) или (22). Характер, положение и масштаб изображений определится расположением точки предмета относительно кардинальных плоскостей и оптической оси системы.
Относительно практического выполнения построений следует обратить
внимание на то, что во все формулы х' и
z' входят только в комбинациях x'/m
и 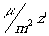 .
Поэтому, если в пространстве изображения расстояния в плоскостях, параллельных
голограмме, измерять в единицах в m раз больших, а в направлении, оси z'
в единицах в .
Поэтому, если в пространстве изображения расстояния в плоскостях, параллельных
голограмме, измерять в единицах в m раз больших, а в направлении, оси z'
в единицах в 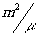 больших, то из формул исчезнут все множители, содержащие
m и m
, главные
плоскости совпадут с плоскостями голограмм, а zF
и равное ему z'F
будут иметь смысл фокусных расстояний.
Другими словами, можно производить все построения без учёта увеличения голограммы
и изменения длины волны, а в окончательном результате растянуть чертёж в
m раз в плоскости голограммы и в
больших, то из формул исчезнут все множители, содержащие
m и m
, главные
плоскости совпадут с плоскостями голограмм, а zF
и равное ему z'F
будут иметь смысл фокусных расстояний.
Другими словами, можно производить все построения без учёта увеличения голограммы
и изменения длины волны, а в окончательном результате растянуть чертёж в
m раз в плоскости голограммы и в 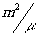 раз в направлении, перпендикулярном к голограмме.
раз в направлении, перпендикулярном к голограмме.
Мы вывели формулы преобразования пространства в голографии из формальных соображений, не опираясь на физические свойства голограммы. Выясним теперь, как физические свойства голограммы согласуются с требованиями проективного преобразования. Рассмотрим окрестности двух близких точек на голограмме во время её получения и окрестности соответственных точек при восстановлении изображения (рис.8). Для того, чтобы в некоторой точке пространства образовалось изображение точки предмета, необходимо, чтобы дифрагированные волны от разных элементов голограммы пришли в эту точку с одинаковыми фазами. Голограмма тем или иным способом запоминает разность фаз q
(х) в точках голограммы между волной, пришедшей от точки предмета и опорной волной. Например, в простейшем случае амплитудной голограммы запоминаются места с одинаковыми фазами.
- 266 -
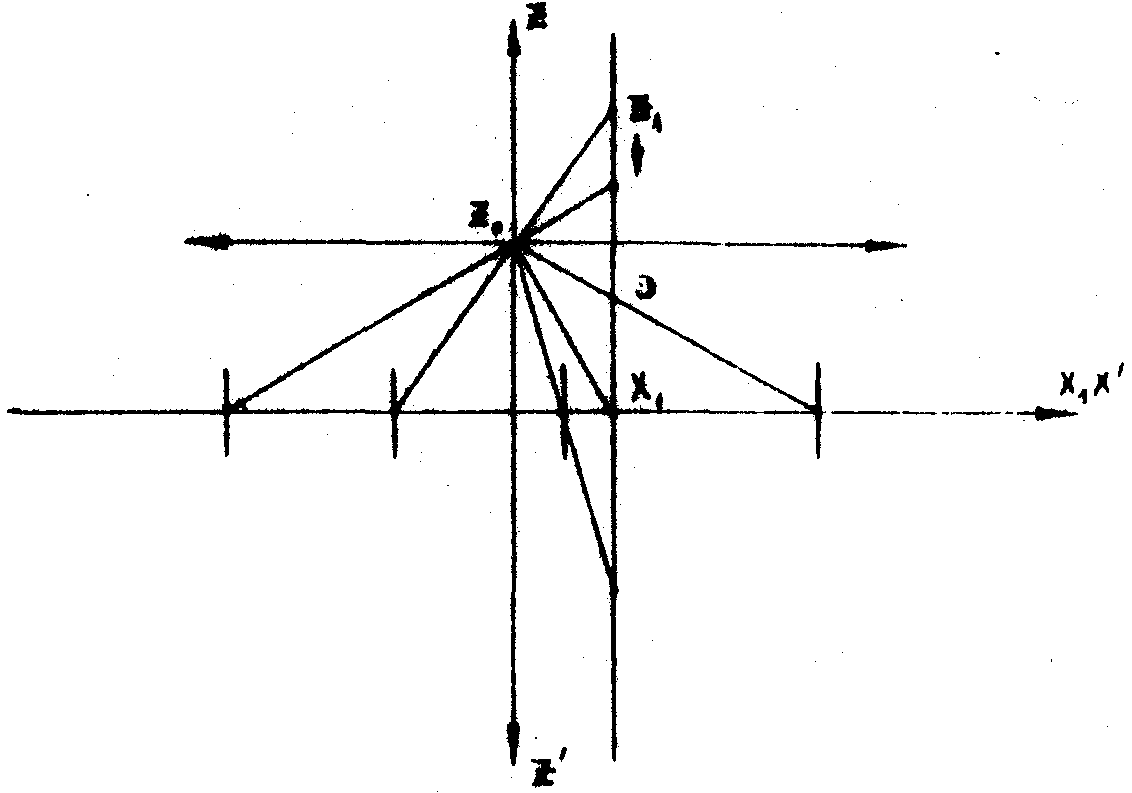
Рис .6 .
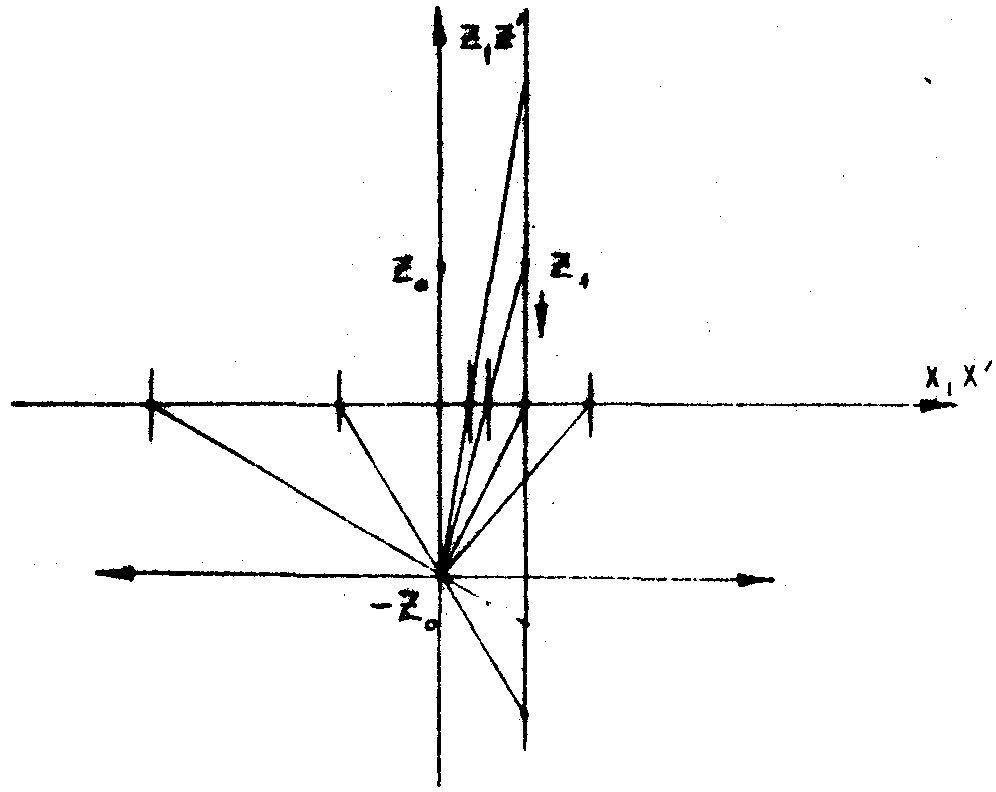
Рис.7.
- 267 -
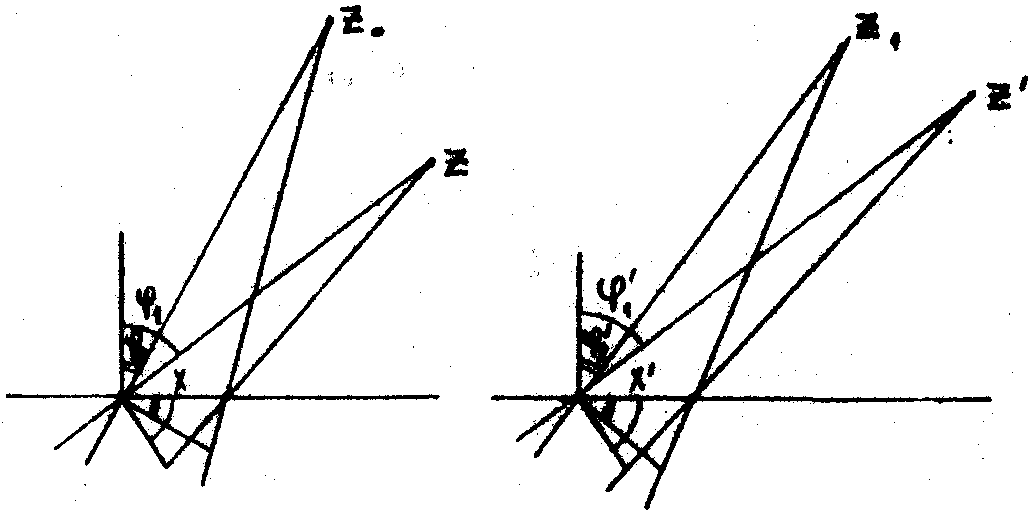
Рис .8.
В случае фазовой голограммы q
(х) записывается в виде фазового рельефа. Для двух близких точек на голограмме, на расстоянии х друг от друга, приращение D
q
дается выражением
D
q
= x(Sinj
1-Sinj
2) (26)
где j
1 и j
2 – углы между нормалью к голограмме и лучами, пришедшими в рассматриваемое место голограммы от точек предмета и опорного пучка.
При восстановлении голограммы, если восстанавливающий свет падает на соответственное место голограммы под углом j
'2, к разности фаз nx'Sinj
'2 между восстанавливающей волной в выбранных точках голограмма добавит D
q
. Если для некоторой точки пространства, лежащей в направлении j
'1, выполняется условие
nx'Sinj
'1 = nx'Sinj
'2+D
q
(27)
то дифрагированные волны придут в эту точку в фазе. Совместное действие воли от разных частей голограммы даст изображение точки. Сравнение (26) и (27) позволяет написать:
- 268 -
x(Sinj
1-Sinj
2) = x'n(Sinj
'1-Sin'j
2) (28)
Сопоставление (2 8) и (14) показывает, что в голографии такая же ситуация, как и в оптике: вместо необходимого для точечного преобразования условия тангенсов выполняется вытекающее на физической природы света условие синусов. Условия (28) и (14), вообще говоря, не совместимы, и голограмма в общем случае дает аберрационное изображение.
Одновременное выполнение (28) и (14) возможно при тех же обстоятельствах, как и в оптике. Учитывая значения x'/x и n, (28) можно записать как
Sinj 1-Sinj
2 = 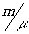 (Sinj
'1-Sinj '2) (Sinj
'1-Sinj '2) (29)
При углах падения, близких в нормали, (29) и (14) выполняются одновременно тем точнее, чем меньше углы, и мы имеем параксиальную голографию аналогично параксиальной оптике. Голограммы, полученные на сравнительно грубых фотоматериалах, параксиальны в силу необходимости малых углов между интерферирующими лучами.
Случаи идеального изображения мы уже перечисляли выше. Из (29)
следует, что для идеального изображения необходимо, чтобы 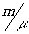 =1,
т.е. при увеличении длины волны, например
при переходе от рентгеновых лучей к видимым, голограмма должна быть увеличена
во столько же раз. Кроме того, одновременное выполнение (29)
и
(14) во всех точках голограммы возможно
только тогда, когда =1,
т.е. при увеличении длины волны, например
при переходе от рентгеновых лучей к видимым, голограмма должна быть увеличена
во столько же раз. Кроме того, одновременное выполнение (29)
и
(14) во всех точках голограммы возможно
только тогда, когда
±
j
'1 = j
1 и ±
j
'2 = j
2 (30)
а это условие выполняется, если
x1 = 0, 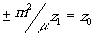 (31)
Мы уже знаем, что эти случаи соответствуют тождественному преобразованию и плоскому зеркалу, и в зависимости от направления хода лучей могут давать действительные или мнимые изображения.
- 269 -
Теперь мы видим, что этим исчерпываются возможности идеального изображения в голографии.
Так как восстановленное и сопряженное изображения появляются одновременно, интересно отметить случай, когда они оба идеальны. Это осуществляется, когда опорные лучки параллельны ( z0=¥
и z1=¥
) и перпендикулярны к поверхности голограммы. Тогда преобразование к восстановленному изображению будет тождественным, а к сопряжённому - зеркальным. Необходимые условия (31) выполняются при этом одновременно для обоих знаков: + и -. Однако, если параллельный опорный пучок падает на плоскость голограммы под углом a
, то сопряжённое изображение уже не будет зеркальным и будет обладать аберрациями. Сопряжённое изображение станет зеркальным и свободным от аберраций, если источник света переместить в симметричное относительно голограммы положение, т.е. изменить направление пучка с a
на -a
.
Относительно возможности осуществления апланатических голограмм
вопрос пока никем не рассматривался, хотя представляет несомненный интерес для
получения увеличенных безаберрационных изображений без увеличения голограммы.
Однако в случае 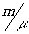 =1
при любом положении источника восстанавливающей
волны существует одна точка, изображающаяся без аберраций. Действительно, если
мы поместим источник света в точку с координатами х'=0,
z'=mz0, то изображение всех
точек предмета в восстановленном изображении будет идеальным. Переместим источник
света в точку х', z'. В
пространстве предмета ей соответствует точка х=х'/m,
z=z'/m. Она изобразится в точку х'=0,
z'=mz0, т.е. на место идеального
положения источника, идеально, что следует из обращения хода лучей (рис.9).
По типу преобразования это изображение относится к сопряжённому изображению,
так как только для него две точки изображаются друг на друга независимо от того
какую из них мы считаем точкой пространства предмета, и какую точкой пространства
изображения. Это свойство преобразований называется
инволюцией. Им обладают, кик легко убедиться,
только зеркальные системы. Тем не менее, эта точка не является апланатической
точкой и условие =1
при любом положении источника восстанавливающей
волны существует одна точка, изображающаяся без аберраций. Действительно, если
мы поместим источник света в точку с координатами х'=0,
z'=mz0, то изображение всех
точек предмета в восстановленном изображении будет идеальным. Переместим источник
света в точку х', z'. В
пространстве предмета ей соответствует точка х=х'/m,
z=z'/m. Она изобразится в точку х'=0,
z'=mz0, т.е. на место идеального
положения источника, идеально, что следует из обращения хода лучей (рис.9).
По типу преобразования это изображение относится к сопряжённому изображению,
так как только для него две точки изображаются друг на друга независимо от того
какую из них мы считаем точкой пространства предмета, и какую точкой пространства
изображения. Это свойство преобразований называется
инволюцией. Им обладают, кик легко убедиться,
только зеркальные системы. Тем не менее, эта точка не является апланатической
точкой и условие
- 270 -
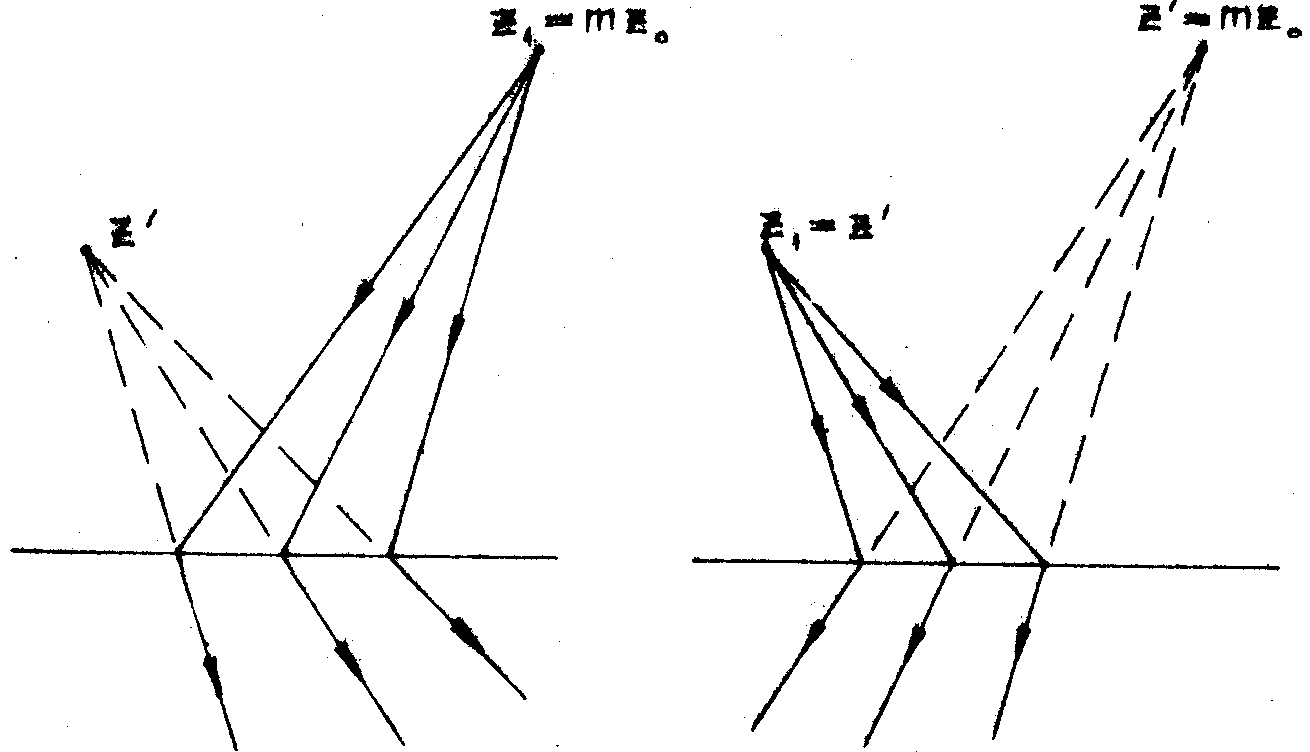
Рис. 9.
синусов для неё не выполняется. Близкие к ней точки должны обладать аберрацией комы.
Интересными свойствами обладает голограмма плоского предмета (диапозитива), параллельного плоскости голограммы, когда источник опорной волны лежит в плоскости диапозитива. Оба изображения для такой голограммы всегда лежат в плоскости точечного источника света и центрально-симметричны относительно его (сопряжённое изображение "вверх ногами"). В общем случае координаты z' изображения зависят от m, поэтому голограммы допускают только однородное растяжение (увеличение). В обсуждаемом случае изображение при любом m лежит в плоскости источника, поэтому такие голограммы допускают разные увеличения по осям координат, точнее произвольное афинное преобразование голограммы, что позволяет осуществить анамарфотное преобразование пространства с
- 271 -
равным увеличением изображения по осям.
При проектировании такой голограммы на экран, если голограмму помещать непосредственно перед объективом, размеры изображения на экране не зависят от фокусного расстояния объектива, что обычно ставит в тупик демонстраторов . Это происходит оттого, что в параксиальной области угловые размеры изображения относительно центра голограммы остаются постоянными при любом положении источника света, а объектив проектирует изображение на экран под тем же углом, под которым он видит предмет. В случае обычного диапозитива сохраняются линейные размеры диапозитива, а угловые зависят от фокусного расстояния объективе. Ещё одна особенность проектирования на экран состоит в том, что перемещение голограммы вдоль оптической оси объектива приводит к уменьшению размеров изображения на экране, но сохраняет его резкость. Это связано с тем, что при перемещении голограммы плоскость восстановленных изображений остаётся неподвижной, совпадая с плоскостью источника света. Проектирование голограмм предметов, не лежащих в плоскости источника, более сложно и может быть разобрано на основании формул (18) и (28), как построение изображения в сложной системе - голограмма + объектив.
В голограммах общего вида, когда опорная волна образуется протяженным источником ("духи"), или в голограммах на толстых эмульсиях и в объёме светочувствительного вещества восстановление изображения возможно только при точном воспроизведении условий получения голограммы. В таких голограммах отсутствует сопряженное изображение, за исключением некоторых симметричных случаев.
Появление сопряжённого изображения в обычных голограммах, свойства которых мы обсудили, связано с тем, что разность фаз q
(х) записывается на голограмме с точностью до целых длин волн, поэтому распределение амплитуды пропускания или фазовый рельеф на голограмме носят периодический характер. При этом удовлетворение условия равенства фаз волн, приходящих в точку изображения, становится возможным для нескольких направлений, в том числе для сопряжённого изображения и для изображений более высоких порядков, если эмульсия нелинейна. Если бы q
(Х) записывалась
- 272 -
как непрерывная функция, то мы получили бы линзу, аберрации которой приводят к тому , что точечный источник света изображается в виде голографируемого предмета. При этом исчезло бы не только сопряжённое изображение, но и изображение самого точечного источника.
Из проведённого рассмотрения совершенно очевидно, что если мы осветим голограмму когерентным предметом, то в пространстве изображения восстановится изображение точечного источника. На этом принципе основана голографическая идея распознавания образов, так как изображение источника возникает и тогда, когда предмет включается в освещающий объект как его часть, а положение восстановленного точечного источника определяется положением предмета в освещающем объекте.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

