КЛАССИФИКАЦИЯ
ГОЛОГРАММ
Л.М.Сороко
В
первой половине лекции излагаются те стороны явления дифракции
света, которые имеют первостепенное значение в голографии.
Во второй части лекции вопрос о классификации голограмм рассматривается
строго на языке операционного формализма в скалярном приближении
теории дифракции.
§
I.
Начнём
с мысленных экспериментов, иллюстрирующих характер деформации
пространственной структуры волнового поля по мере удаления
плоскости наблюдения от транспаранта (рис.1). В приведённой
схеме коллимированный пучок монохроматического света П освещает
транспарант t. Изображающая система, состоящая из линзы Л
и экрана Э, даёт возможность наблюдателю видеть пространственную
структуру волнового поля в разных плоскостях. Смена плоскостей
достигается поступательным перемещением изображающей системы.
Если
в начальном положении наблюдатель видит изображение самого
транспаранта, состоящего в простейшей примере. из совокупности
точечных проколов в непрозрачном экране, то при перемещении
изображающей системы вправо каждая яркая точка постепенно
размывается в некоторую фигуру дифракции. Картина, которая
возникает при малых перемещениям, называется дифракцией Френеля.
При больших удалениях изображающей системы от транспаранта
образуется сложный узор.
По
мере увеличения расстояния q наблюдается возрастание размера
колец дифракционной картины Френеля. Наконец, возникает такая
геометрия, что размеры центральной зоны Френеля превосходят
размеры самого транспаранта. Это картина дифракции далёкого
поля, образующаяся при таких больших расстояниях q,
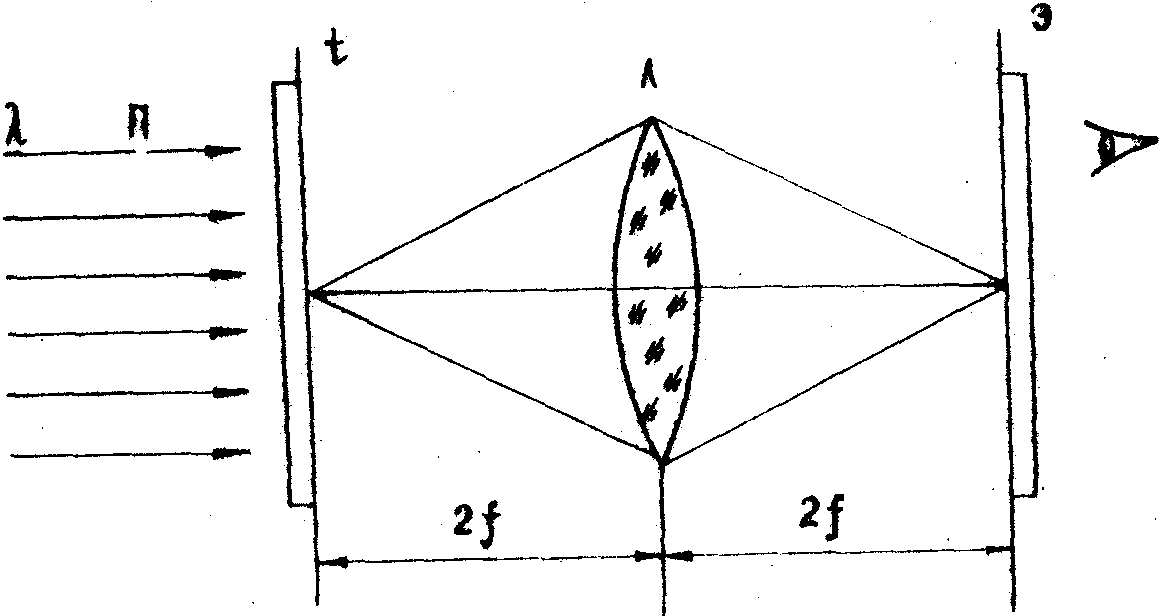
Рис.
1
Схема
наблюдения пространственной структуры волнового поля на
различных расстояниях q за транспарантом t:
Л
- собирающая линза с фокусным расстоянием f;
Э
- экран.
что
размеры транспаранта уже недостаточны, чтобы передать информацию
о кривизне волнового фронта или же расходимости лучей света.
Поэтому картина дифракции далёкого поля или дифракции Фраунгофера
отображает лишь картину направления лучей, идущих от транспаранта
под всевозможными углами.
Теперь
перейдём к другому численному эксперименту (рис.2), в котором
в качестве транспаранта взята дифракционная решётка, создающая
только первый порядок дифракции. Вторичные лучи выйдут из
транспаранта под углом ±q =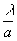 ,
где а- шаг решётки, l -длина волны света. В явном виде
здесь не образуется картины, состоящей из колец Френеля. Переход
от одного вида транспаранта - точечных протоколов в непрозрачном
экране- к другому виду - дифракционной решётке - эквивалентен
переходу от одного представления к другому. В этом втором
представлении наше внимание сосредоточено на распределении
вторичных лучей по углам. Чтобы воспроизвести картину направлений
этих лучей, следует уйти от транспаранта на такое большое
расстояние, чтобы дифрагированная волна заняла на экране наблюдения
сравнительно небольшое пятнышко. На экране наблюдатель увидит
картину дифракции Фраунгофера, отображающую пространство направлений
дифрагированных лучей. Это обеспечивается тем, что в этих
условиях предмет-транспарант настолько удален от экрана (рис.5),
что его размерами можно пренебречь
,
где а- шаг решётки, l -длина волны света. В явном виде
здесь не образуется картины, состоящей из колец Френеля. Переход
от одного вида транспаранта - точечных протоколов в непрозрачном
экране- к другому виду - дифракционной решётке - эквивалентен
переходу от одного представления к другому. В этом втором
представлении наше внимание сосредоточено на распределении
вторичных лучей по углам. Чтобы воспроизвести картину направлений
этих лучей, следует уйти от транспаранта на такое большое
расстояние, чтобы дифрагированная волна заняла на экране наблюдения
сравнительно небольшое пятнышко. На экране наблюдатель увидит
картину дифракции Фраунгофера, отображающую пространство направлений
дифрагированных лучей. Это обеспечивается тем, что в этих
условиях предмет-транспарант настолько удален от экрана (рис.5),
что его размерами можно пренебречь
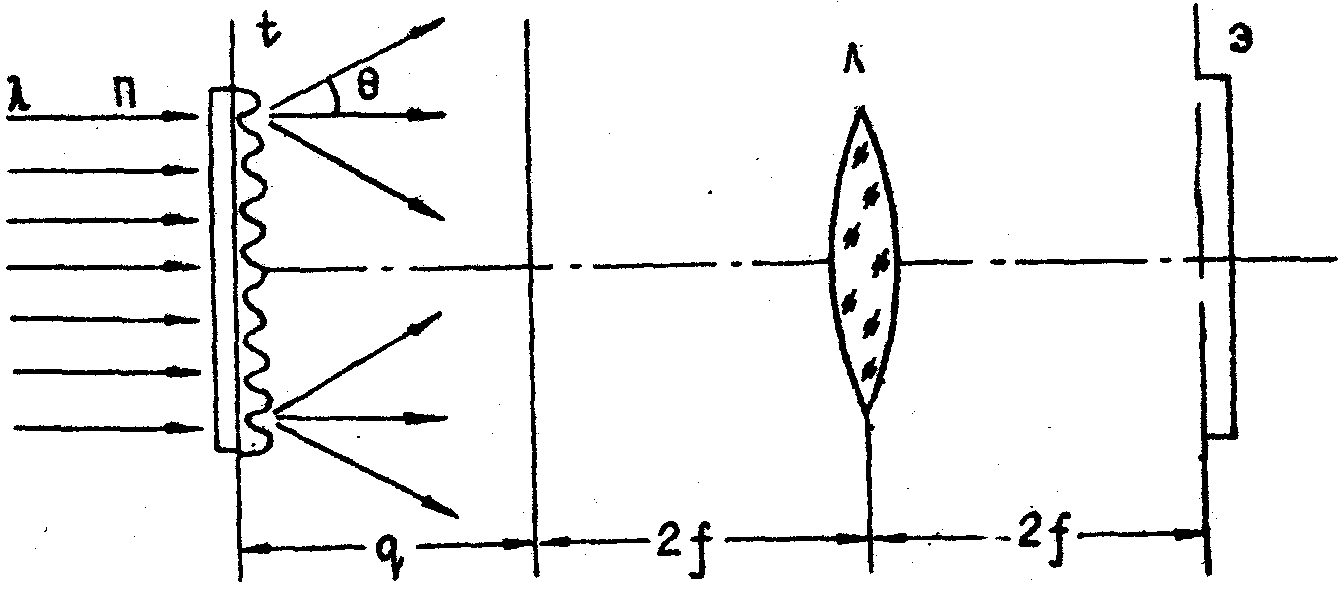
Рис.2.
Волновое поле на расстоянии q за дифракционной решёткой
состоит из трёх изображений пучка.
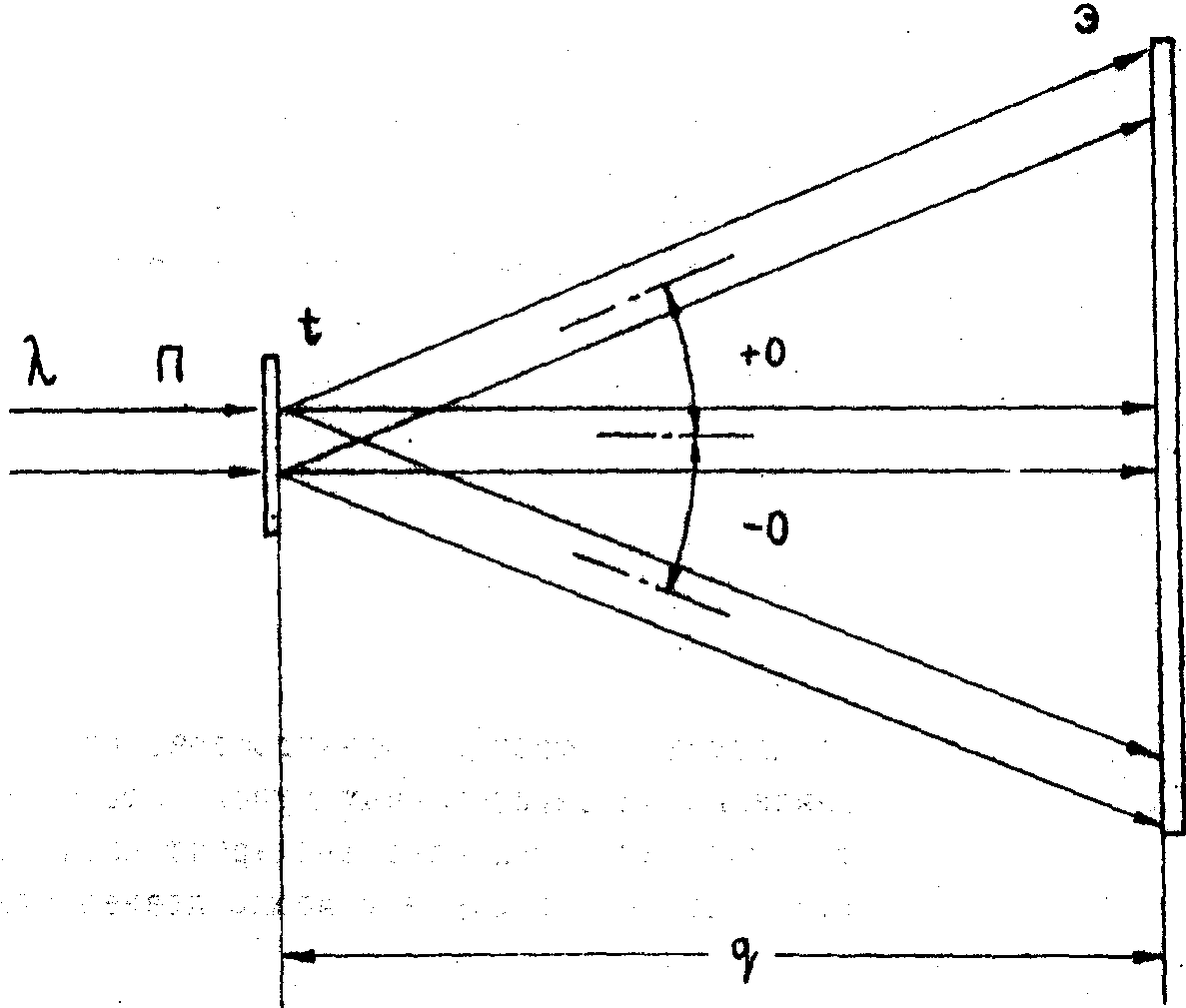
Рис.5.
Схема наблюдения картины дифракции Фраунгофера на большом
экране, расположенном далеко от транспаранта.
и
считать, что дифрагированные лучи разных направлений выходят
как бы из одной точки. В случае идеальной дифракционной решётки
лучи распространяются под тремя направлениями: +q , 0
, -q .
Совершенно
ясно, что схема наблюдения картины дифракции Фраунгофера в
оптическом диапазоне, сопряжённая с изготовлением экрана столь
огромных размеров, является абсолютно непрактичной, и она
была здесь приведена только для иллюстрации. Отображение пространства
направлений гораздо удобней осуществить иначе - с помощью
преобразующей собирающей линзы (рис.4). В этой схеме совокупность
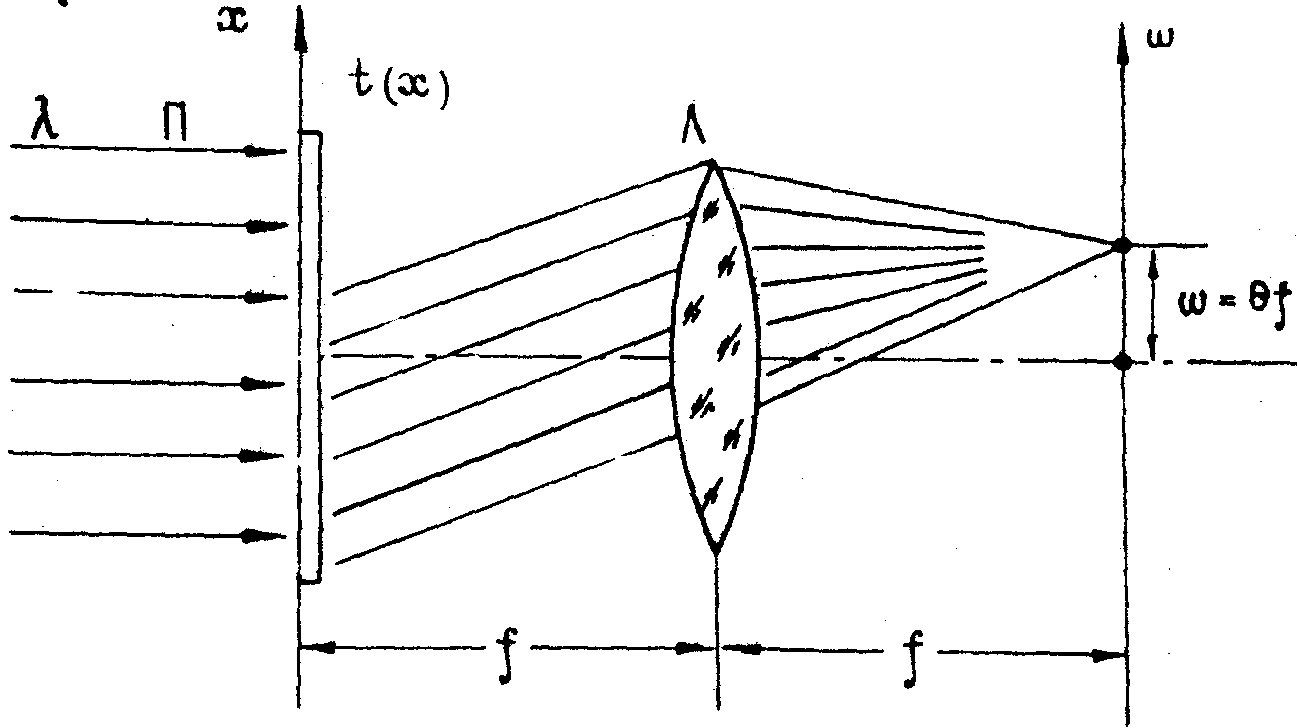
Рис.4.
Схема отображения картины распределения лучей, дифрагированных
на транспаранте t(х) с помощью собирающей линзы Л.
Каждой
точке w (w х,w у)
на частотной плоскости w соответствует направление
лучей q (q х,q у).
лучей,
выходящих из различных точек транспаранта и идущих под одним
и тем же углом q , собирается линзой в одну точку на
частотной плоскости.
Картину
дифракции далёкого поля или дифракции Фраунгофера можно наблюдать
по несколько другой схеме, которая имеет большое фактическое
значение (рис.5). Транспарант t(x), дифракцию далёкого поля
от которого мы хотим наблюдать, размещается непосредственно
позади собирающей линзы Л. Картина дифракции далёкого поля
отображается в фокальной плоскости w собирающей линзы
Л независимо от положения транспаранта относительно линзы
Л. Именно в такой схеме наиболее полно соблюдается пространственная
инвариантность процесса отображения, а сопутствующие аберрации
оказываются малыми по сравнению с аберрациями в любой другой
схеме получения дифракции далёкого поля. Напомним здесь, что
главное условие малости поправок к операционному формализму
в реальной оптической системе - это малость апертурного угла
собирающей линзы.
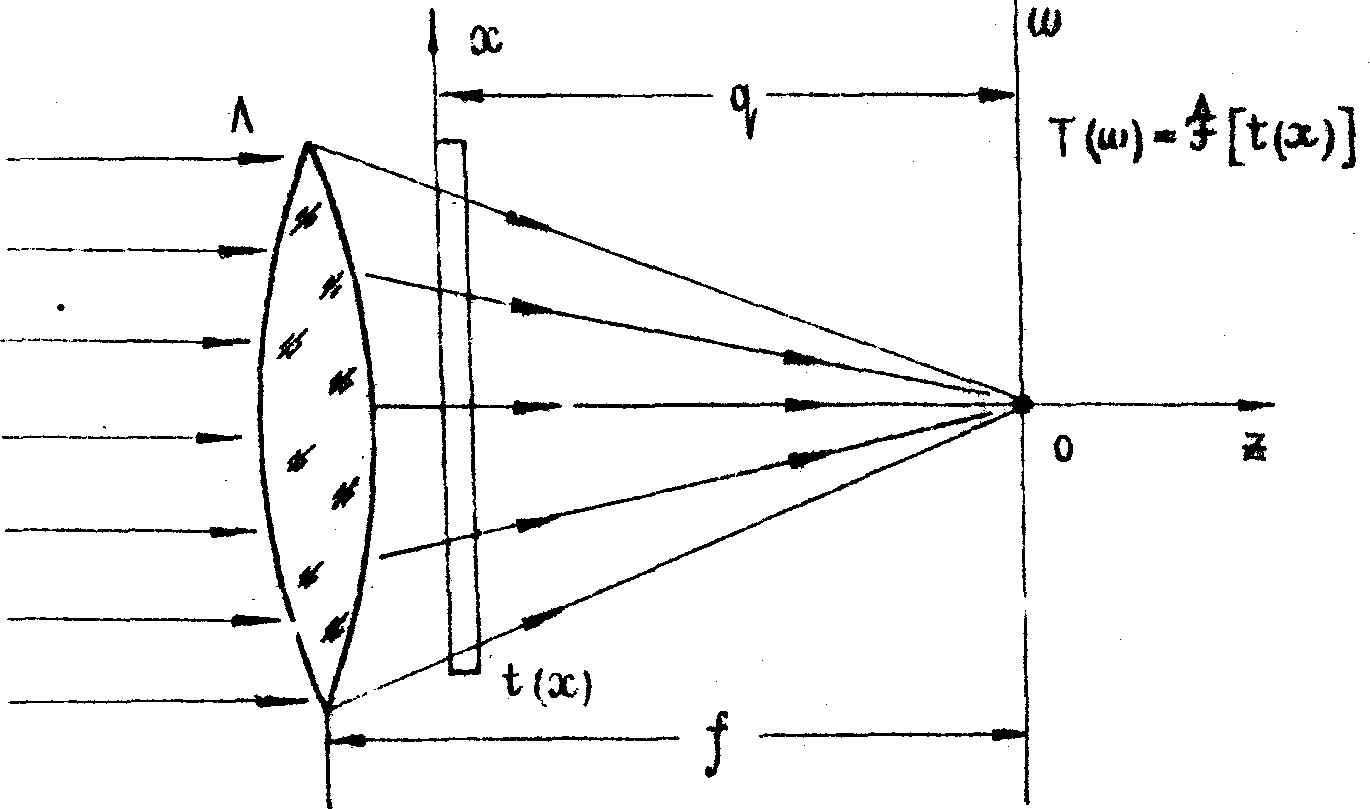
Рис.5.
Полезная практическая схема получения картины дифракции
далёкого поля. Транспарант t(x) устанавливается за линзой
Л. В плоскости w отображается Фурье-образ сигнала
t(x). Линза Л создаёт в плоскости w картину дифракции
далёкого поля.
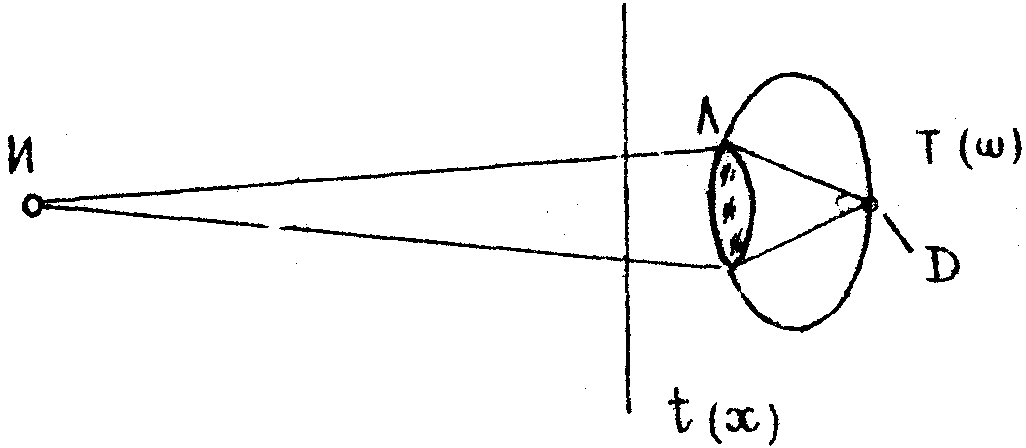
Рис.6.
Схема наблюдения картины дифракции далекого поля простым
глазом: И - точечный источник, расположенный на конечном
расстоянии от наблюдателя; t. - транспарант; D - изображение
источника И на сетчатке.
Небезынтересно
отметить, что картину дифракции далёкого поля можно наблюдать
простым глазом (рис.6). Точечный источник света И может быть
расположен на конечном расстоянии от наблюдателя. Зрачок глаза
образует на сетчатке действительное изображение источника
в виде "точки" D. Если на пути лучей поместить транспарант
t, то в окрестности точки появится картина дифракции далёкого
поля, отображающая направленность лучей, испытавших дифракцию
в транспаранте. Важно, чтобы транспарант располагался как
можно ближе к глазу, так, чтобы исключить возможность аккомодации
глаза по фокусу на самом транспаранте. При этом регулярные
структуры, например, тканевые занавеси на окнах, создают узоры
дифракции далёкого поля даже от уличных фонарей, т.е. когда
источник света достаточно размыт.
Принципы
подразделения геометрии опыта на различные области дифракции
имеют прямое отношение к принципам классификации голограмм.
Однако соотношение между областью дифракции и типом голограммы
довольно сложное и зависит также от степени расходимости предметного
и опорного пучков и относительного расположения источников.
Рассмотрим
сначала простейший случай - схему получения голограмм с использованием
параллельных лучков света. Анализ начнём с выяснения вопроса
о том, каким образом волновое поле в плоскости голограммы
связано с амплитудным пропусканием транспаранта (рис.7). В
данной схеме параллельный пучок света создаётся точечным источником
света S и коллимированной линзой Л. Транспарант расположен
в плоскости x (x ,h ). На расстоянии q от транспаранта,
в плоскости х(х,у), установлена фотопластинка, на которой
регистрируется голограмма. Наша задача состоит в том, чтобы
найти соотношение между амплитудным пропусканием транспаранта
t(x ) и волновым полем в плоскости фотопластинки, описываемым
оптическим сигналом u(x). При этом предполагается, что источник
света обладает требуемыми характеристиками, т.е. имеет необходимую
временную и пространственную когерентность.
В
общем виде поставленную задачу решить очень трудно. Однако
в определённых условиях ее можно решить приближенно,
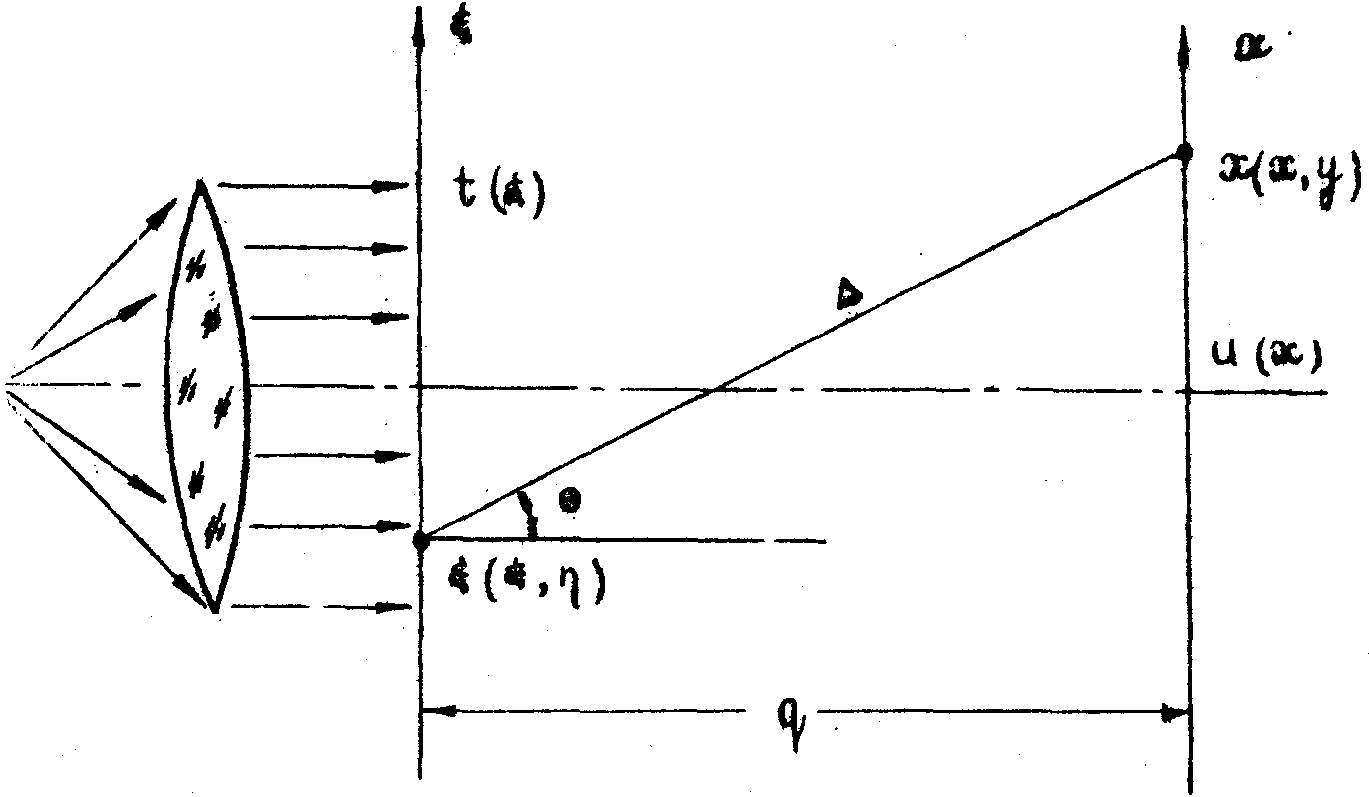
Рис.7.
Схема, поясняющая метод установления связи между волновым
полем u(x) в плоскости голограммы и амплитудным пропусканием
транспаранта t(x ), который освещается когерентным
коллимированным пучком света.
воспользовавшись,
например, формулой Кирхгофа. Приближение Кирхгофа-Френеля
является скалярной теорией, в которой полностью пренебрегается
явлениями поляризации света. При определённых геометрических
условиях волновое поле в плоскости фотопластинки можно представить
в следующем виде:
u(x)=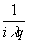 ∫t(x
)eikD dx (1)
∫t(x
)eikD dx (1)
где
К=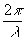 , а D
- длина отрезка, соединяющего точку x (x ,h
) на транспаранте с точкой х(х,y) на фотопластинке.
, а D
- длина отрезка, соединяющего точку x (x ,h
) на транспаранте с точкой х(х,y) на фотопластинке.
Для
большинства задач голографии это приближение достаточно подходящее.
Оно позволяет строго рассмотреть проблему дифракции света
и сформулировать теорию классификации голограмм.
Если
размеры транспаранта и фотопластинки малы по сравнению с расстоянием
q между ними, то можно ограничиться первым порядком приближения.
Тогда
D
@ q + 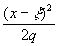 º q +
º q + 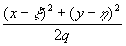 (2)
(2)
В
этом приближении оптический сигнал u(x) равен
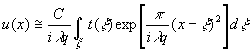 (3)
(3)
где
C
= eikq (4)
Воспользуемся
теорией функции Френеля. Введём двухмерную функцию Френеля
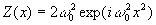 (5)
(5)
где
параметр функции Френеля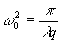 или
или
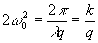 (6)
(6)
Опуская
постоянный множитель в (3) и вводя сокращённое обозначение
для интегральной операции свёртки, находим
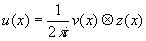 (7)
(7)
Это
соотношение составляет основу операционного формализма теории
дифракции. Подчеркнём, что область применимости этой операционной
теории ещё не очерчена с полной строгостью. Как правило, требования
к области применимости соотношения (7) стремятся выполнить
о запасом, сохраняя некоторую излишний осторожность.
Соотношение
(7) отвечает простейшей картине дифракции Френеля, когда каждая
точка на транспаранте размывается в функцию Френеля. Это наиболее
типичный случай. Однако в зависимости от степени размытости
каждой элементарной картины реализуются весьма важные крайние
случаи. В первом случае, при слабой размытости, волновое поле
u(x) приближается к виду самого транспаранта t(x). Во втором
крайней случае дифракционное размытие волнового поля становится
настолько большим, что на фотопластинке не умещается даже
одна центральная зона Френеля.
Для
строгого рассмотрения этого случая представим выражение (7)
в других формах. Воспользуемся тем, что Фурье-образ функции
Френеля (5) равен
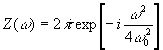 (8)
(8)
где
w
2 = w х2 + w у2 (9)
Воспользуемся
такаю следующей теоремой:
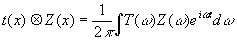 (10)
(10)
где
T(w
)=∫t(x)e-iw xdx (11)
Фурье-образ
функции t(x), a
t(x)=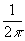 ∫T(w
)eiw xdw (12)
∫T(w
)eiw xdw (12)
Если
операцию свёртки t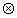 z
записать в развёрнутом виде, то получим
z
записать в развёрнутом виде, то получим
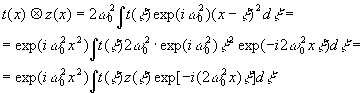 (13)
(13)
Используя
далее теорему о том, что
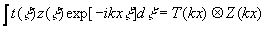 (14)
(14)
окончательно
получим
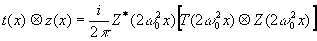 (15)
(15)
где
также учтено, что
exp(iw
02x2) = 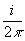 Z*(2w
02x) (16)
Z*(2w
02x) (16)
Таким
образом, исходное наиболее общее соотношение (7) может быть
представлено в следующих формах:
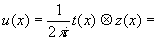 (17а)
(17а)
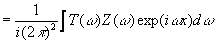 (17б)
(17б)
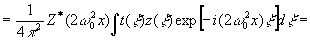 (17в)
(17в)
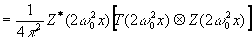 (17г)
(17г)
Альтернативные
формы записи волнового поля u(x), представленного в (17),
позволяют чётко сформулировать правила разграничения на различные
области дифракции. Для этого необходимо ввести три характеристические
длины:
1)
размер предмета-транспаранта а;
2)
размер центральной зоны Френеля ℓ;
3)
размер наиболее мелкой детали предмета-транспаранта d
.
Размер
центральной зоны Френеля равен
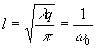 (18)
(18)
и
связан с параметром w 0, который определяет
масштаб картины Френеля.
Размер
наиболее меткой детали предмета d связан с максимальной
пространственной частотой W 0, имевшейся в
пространственной структуре транспаранта t(x ), соотношением
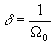 (19)
(19)
Теперь
мы можем разграничить следующие области дифракции.
I.
Область дифракции далекого поля
Размер
предмета значительно меньше размера центральной зоны Френеля,
т. е.
а
<< ℓ (20)
Иначе
это можно записать так:
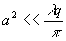 или
ещё проще; a2 << l q (21)
или
ещё проще; a2 << l q (21)
Иногда
условие (21) записывают в виде
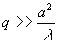 (22)
(22)
а
параметр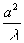 называют
индексом далёкого поля.
называют
индексом далёкого поля.
Условие
(20) эквивалентно соотношению
аw
0 << 1 (23)
а
это означает, что функция Френеля Z(x ) согласно определению
(5) и условию (23) равна постоянной величине. Её можно вынести
за знак интеграла в (17в). Если далее воспользоваться равенством
(16), то окончательно получим
u(x)
@ T(2w 02x) (24)
В
области дифракции далёкого поля оптический сигнал u(x) в плоскости
фотопластинки равен Фурье-образу амплитудного пропускания
транспаранта.
2.
Область геометрической тени
Размер
центральной зоны Френеля значительно меньше размера наиболее
мелкой детали транспаранта Дифракционное размытие настолько
мало, что не искажает вид самой мелкой детали на транспаранте.
На фотоэмульсию проектируется тень от транспаранта.
Условие
ℓ
<< d (25)
или
с учётом (18)
w
0
>> W 0
эквивалентно
условию
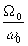 << 1
<< 1
которое
означает, что максимальная пространственная частота на транспаранте
значительно меньше частоты w 0, определяющей
масштаб картины Френеля в выражении (5). Это приводит к тому,
что Фурье-образ функции Френеля Z(w ) практически равен
1 и его можно вынести за знак интеграла в (I7б). Окончательно
получим
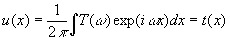 (27)
(27)
Таким
образом, амплитуда волны в плоскости фотоэмульсии равна амплитудному
пропусканию транспаранта.
Величину
d можно иначе рассматривать как разрешающую способность
изображающей системы. В этом случае условие (25) означает,
что разрешающая способность изображающей системы такова, что
она не позволяет обнаружить элементы дифракционной картины
Френеля при малых значениях q.
5.
Область дифракции Френеля
Общий
случай дифракции Френеля определяется условием
d
< ℓ < а (28)
Размер
центральной зоны Френеля больше самой мелкой детали транспаранта,
но меньше размера самого транспаранта.
§
2.
При
переходе от параллельного освещения к расходящимся или сходящимся
пучкам, используемым как на стадии получения голограммы, так
и на стадии восстановления, анализ структуры волнового поля
u(x) существенно усложняется, так как здесь возникает много
свободных параметров.
Ограничимся
рассмотрением простейшего случая, когда длины волн света одинаковы
на обеих голографических стадиях, а поэтому не возникает необходимости
изменять геометрию опыта при переходе от одной стадии к другой.
Таким образом, рассмотрению достаточно подвергнуть лишь стадию
получения геометрии, которая осуществляется по следующей схеме
(рис.8).
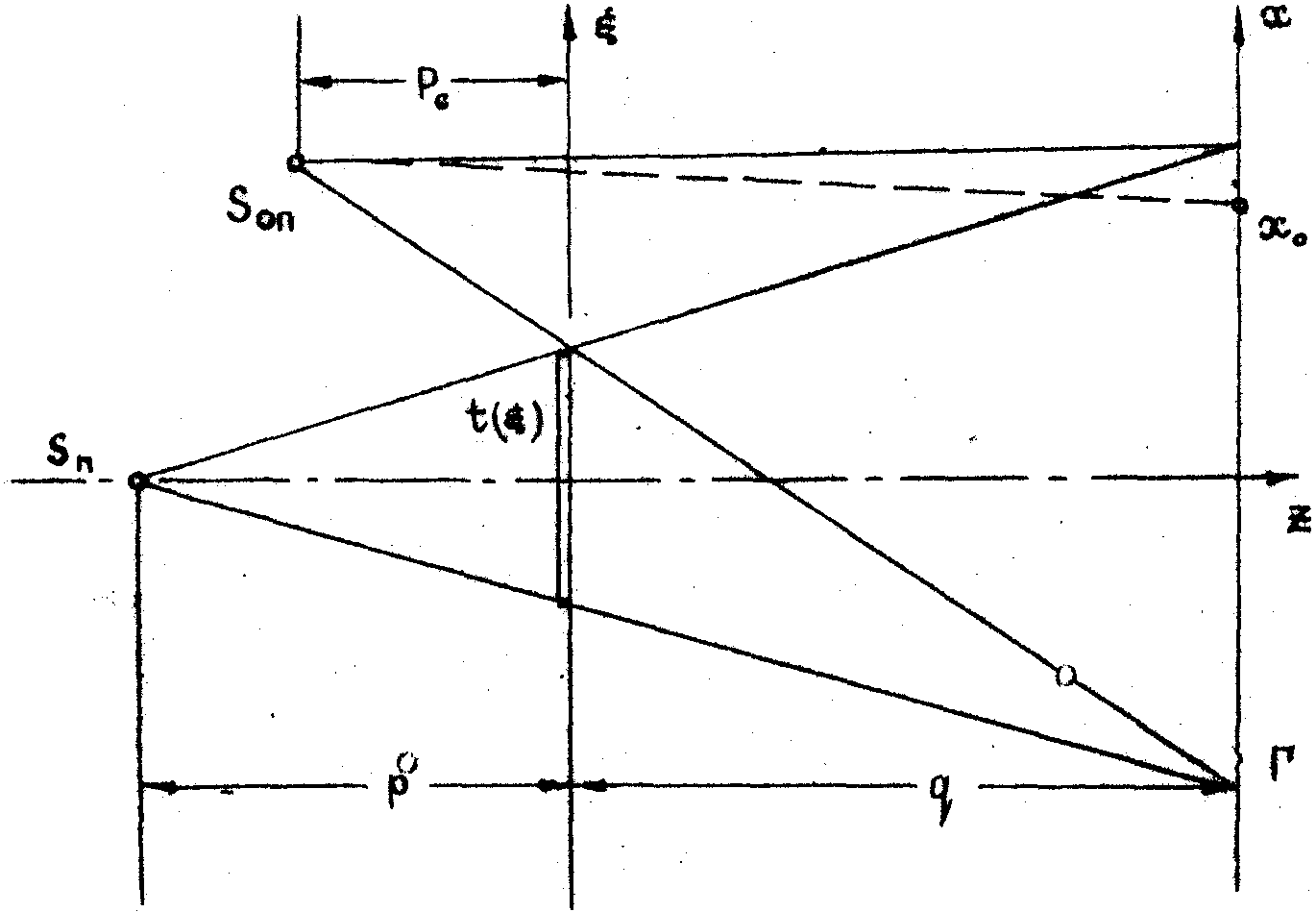
Рис.8.
Схема, поясняющая анализ пространственной структуры голограммы
Г при использовании неколлимированных пучков.
Источник
Sn, освещающий транспарант, установлен на оси z
на расстоянии р перед транспарантом. Опорный источник Son
находится на расстоянии рс перед транспарантом
в точке, проекция которой на плоскость х имеет координату
х0. Фотопластинка Ф расположена в плоскости х на
расстоянии q за транспарантом. Геометрические параметры р,
q и рс являются алгебраическими величинами. Так,
например, если р<0, то это означает, что освещающий пучок
является сходящимся.
Геометрический
фактор предметного пучка равен
М
= 1 + 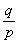 (29)
(29)
Геометрический
фактор опорного пучка равен
Мс
= 1 + 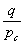 (29)
(29)
В
отсутствие транспаранта волновое поле в плоскости фотопластинки
складывается из двух расходящихся волн:
U0(x)
= Î c(x) + Î 0(x) (31)
где
Î
c(x) = Acexp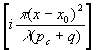 (32)
(32)
Î
0(x) = A0exp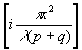 (33)
(33)
После
внесения транспаранта t(x ) в предметный пучок волновое
поле в плоскости фотопластинки станет равным
U(x)
= Î c(x) + Î 0(x)t (r
) (34)
где
t
(r ) = t(r )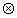 zв(r
) (35)
zв(r
) (35)
и
r
= 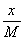 , В2
= w 02М, w 02
=
, В2
= w 02М, w 02
=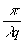 (36)
(36)
-
59 -
Амплитудное
пропускание полученной голограммы равно
t(x)=ï
u(x)ï 2=ï Î c(x)ï
2+ï Î 0(x)t (r )ï
2+tмним(х)+tдейств(х) (37)
где
tмним
= t*действ = Cexp(iW x)t (r
)exp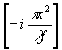 (38)
(38)
W
= 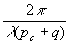 (39)
(39)
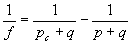 (40)
(40)
Назовём
сферическим френелевским образом транспаранта функцию
y
(x) = exp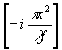 [t(r
)
[t(r
)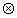 Zв(r
)] (41)
Zв(r
)] (41)
По
аналогии с выражением (7), справедливым для плоских освещающего
и опорного пучков, функцию y (x) можно представить в
разных видах. А именно:
y
(x) = exp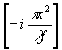 [t(r
)
[t(r
)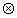 Zв(r
)] (42а)
Zв(r
)] (42а)
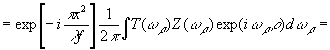 (42б)
(42б)
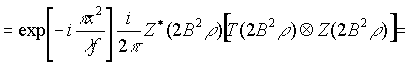 (42в)
(42в)
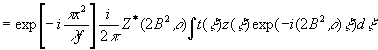 (42г)
(42г)
Выражение
(42в) и (42г) можно записать также в следующем виде
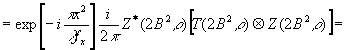 (42в')
(42в')
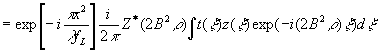 (42г')
(42г')
где
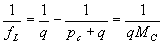 (43)
(43)
Для
выявления основных областей дифракции введём три характеристические
длины:
1)
размер предмета-транспаранта а;
2)
размер центральной зоны Френеля
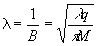 (44)
(44)
3)
размер наименьшей детали предмета-транспаранта d =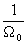
Принцип
строгой классификации голограмм основан на анализе пространственной
структуры сферического Френелевского образа y (х) и его
Фурье-образа y (w ). Точный вид Функций y (х)
и y (w ) определяется условиями опыта и будет приведён
ниже. Если голограмма получается в опыте с использованием
расходящихся пучков, то вид функций y (х) и y (w
) определяется следующими факторами;
1)
относительным расположением транспаранта и двух источников
-опорного Sоп и предметного Sп (геометрические
параметры р, q, pc и x0);
2)
областью дифракции, в которой регистрируется голограмма (параметры
d , ℓ, а).
В
самом общем случае голограммы можно разбить на четыре типа:
тенеграмму, голограмму Френеля, голограмму квази-Фурье, голограмму
Фурье. Каждому типу голограммы соответствует определённая
структура функций y (х) и y (w ). Возможные
виды структур этих функций приведены в следующей таблице.
Таблица
1
|
Тип голограммы
|
Структура
y (х)
|
Структура
y (w
)
|
|
Тенеграмма
|
t(a
x)
|
T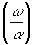
|
|
Голограмма Френеля
|
t(a
x) 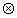 exp(ip
b x2) exp(ip
b x2)
|
t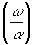 exp exp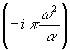
|
|
Голограмма квази-Фурье
|
T(a
x)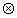 exp(ip
b x2) exp(ip
b x2)
|
t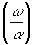 exp exp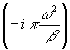
|
|
Голограмма Фурье
|
T(a
x)
|
t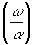
|
Для
того, чтобы найти в явном виде условия, при которых получается
данный тип голограммы, необходимо произвести анализ стадии
получения голограммы в каждой области дифракции, введя для
каждой области дифракции характеристическую длину дополнительно
к размеру центральной зоны Френеля ℓ. Сопоставляя эту
характеристическую длину с деталями и размером предмета и
пользуясь таблицей 2, приведённой ниже, можно установить тип
голограммы и уяснить связь между геометрическими параметрами
голографической установки и типом получающейся голограммы.
Сферический
Френелевский образ транспаранта y (х) имеет согласно
(41) следующую структуру.
y
(х) = y 1(х)[y 2(х)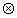 y
3(х)] (45)
y
3(х)] (45)
При
переходе к Фурье-образу,
y
(w )=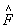 [y
(х)] (46)
[y
(х)] (46)
операция
свёртки заменится на операцию умножения, а операция умножения
- на операцию свёртки. Тогда
y
(w ) = y 1(w )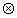 [y
2(w )y 3(w )] (45)
[y
2(w )y 3(w )] (45)
где
y
i(w )=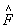 [y
i(х)], i=1,2,3 (46)
[y
i(х)], i=1,2,3 (46)
Вводя
функцию Френеля z(x) согласно (5), запишем функцию y
(х) так:
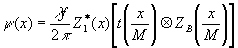 (49)
(49)
ZB(x)
= 2B2exp(iB2x2) (50)
тая
что переход от z(x) к ZB(x) совершается путём замены
w 02 на В2=Мw 02.
Далее, обращаясь к фундаментальным свойствам преобразования
Фурье и Френеля, находим следующие формулы преобразования:
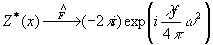 (51)
(51)
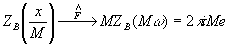 (52)
(52)
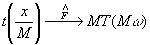 (53)
(53)
?Находим
Фурье-образ y 1(w ) функции (42а):
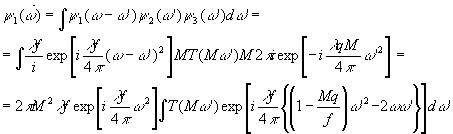 (54)
(54)
Для
нахождения Фурье-образа y 3(x) функции y
(x), представленной в виде (42в'), воспользуемся следующими
формулами преобразования:
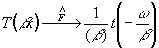 (55)
(55)
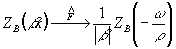 (56)
(56)
где
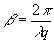 (57)
(57)
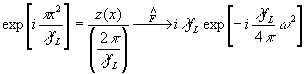 (55)
(55)
Тогда
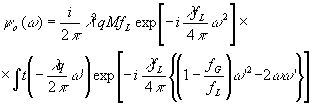 (59)
(59)
где
¦
G = Mq (60)
§
3.
Голограмма
регистрируется в области дифракции Френеля d <ℓ<а
Предположим,
что выполнены условия, позволяющие пренебречь в экспоненте
выражения (54) функции y 1(w ) членами,
квадратичными по w '. Тогда
y
1(w ) » t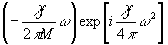 (61)
(61)
Такое
приближенное выражение для y 1(w ) возможно
при условии, если
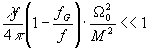 (62)
(62)
или
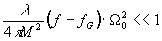 (63)
(63)
Для
осуществления аналогичного приближения в выражении (59) для
y 3(w ), приводящего к
y
3(w ) » Т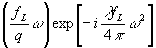 (64)
(64)
требуется,
чтобы
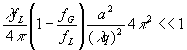 (65)
(65)
или
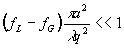 (66)
(66)
легко
видеть, что
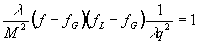 (67)
(67)
Для
того, чтобы убедиться в справедливости (67), воспользуемся
тем, что
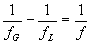 (68)
(68)
Последнее
соотношение вытекает из следующих равенств:
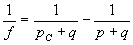 (40)
(40)
 (43)
(43)
¦
L = qMC, ¦ G
= Mq (60)
Равенство
(67) позволяет объединить неравенства (63) и (66) путём введения
характеристической длины дифракции Френеля ℓФ:
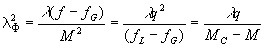 (69)
(69)
Тогда
неравенства (63) и (66) запишутся в компактном виде:
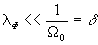 (69)
(69)
ℓФ
>> a (69)
Сопоставляя
выражение (61) и (64) с образцами выражений в табл.1, мы можем
сделать вывод о том, что в области дифракции Френеля, когда
d <ℓ<а и ℓФ<<d
, регистрируются голограммы квази-Фурье, а если ℓФ>>а,
то регистрируется голограмма Френеля.
Голограмма
регистрируется в области геометрической тени ℓ<d
В
области геометрической тени аргумент функции Z(w r
), входящей в подынтегральное выражение (42б), можно положить
равным нулю, а само значение Z(0) вынести за знак интеграла.
Функция y (х) в области геометрической тени приближенно
равна
 (70)
(70)
Условие
геометрической тени ℓ<d можно записать в виде
ℓ2W
02 << 1 (71)
Тогда,
поскольку
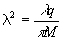 (72)
(72)
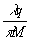 W
02
<< 1 (73)
W
02
<< 1 (73)
и
можно пренебречь вторым слагаемым в экспоненте подынтегрального
выражения (54). Тогда
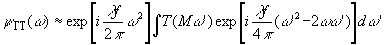 (74)
(74)
далее,
если
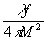 W
02
<< 1 (75)
W
02
<< 1 (75)
то
можно пренебречь квадратичными членами по w ' в той же
экспоненте и
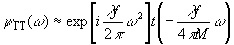 (76)
(76)
Учитывая
соотношения (68) и (60), мы можем записать
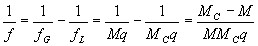 (77)
(77)
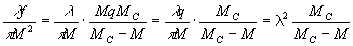 (78)
(78)
Определим
характеристическую длину в области геометрической тени:
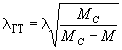 (79)
(79)
Тогда
условие (75) запишется в виде
ℓГТ2W
02 << 1 (80)
Если
теперь обратиться к функции y ГТ(х) в области
геометрической тени (70), то легко видеть, что фазой в экспоненте
или кривизной волнового фронта волны в этом выражении можно
пренебречь, если
М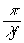 а2
<< 1 (81)
а2
<< 1 (81)
Поскольку
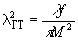 (82)
(82)
то
условие (81) можно записать в таком виде:
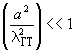 (83)
(83)
и
функция y ГТ(х) примет вид:
y
ГТ(х)» 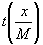 (84)
(84)
Сопоставляя
выражения (78) и (84) с образцами выражений в табл.1, мы видим,
что в области геометрической тени, когда ℓ<d
и ℓГТ<<d , регистрируется голограмма
квази-Фурье, а если ℓГТ>>a, то регистрируется
тенеграмма
Голограмма
регистрируется
в
области дифракции далекого поля ℓ>a
Произведя
анализ, аналогичный предыдущим случаям, можно убедиться в
том, что в области дифракции далёкого поля
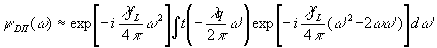 (85)
(85)
Если
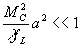 (86)
(86)
то
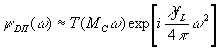 (74)
(74)
Из
(86) видно, что xаpактeриcтичecкoй длиной в области далекого
поля является
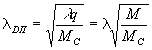 (88)
(88)
и
тогда
ℓDП
>> a (89)
Далее,
если
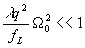 или
или 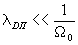 (90)
(90)
то
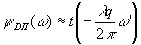 (91)
(91)
Сопоставляя
выражения (87) и (91) с образцами выражений в табл.1. мы видим,
что в области дифракции далёкого поля, когда ℓ>а
и 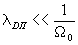 регистрируется
голограмма Фурье, а если ℓDП >> a,
то - голограмма Френеля. Результаты приведённого анализа можно
свести в следующую таблицу.
регистрируется
голограмма Фурье, а если ℓDП >> a,
то - голограмма Френеля. Результаты приведённого анализа можно
свести в следующую таблицу.
|
Условия
реализации
|
Голограмма Фурье
|
-
|
-
|
ℓDП<
d
|
|
Голограмма квази-Фурье
|
ℓФ<
d
|
ℓГТ<
d
|
-
|
|
Тенеграмма
|
-
|
а<
ℓГТ
|
-
|
|
Голограмма Френеля
|
а<
ℓФ
|
-
|
А<
ℓDП
|
|
Голограмма общего вида
|
d
< ℓФ<
а
|
d
< ℓГТ<
а
|
d
< ℓDП<
а
|
|
Характеристическая
длина для данной области дифракции
|
|
|
|
|
Общие
характеристичес-кие длины
|
Размер центральной зоны Френеля,
|
Размер а предмета
|
Размер наименьшей детали предмета
d
|
|
Область дифракции
|
Область дифракции Френеля,
d
< ℓ<
а
|
Область геометричес-кой тени,
ℓ<
d
|
Область дифракции далекого поля,
ℓ>a
|
Отметим
один наиболее интересный и важный случай получения голограммы
Фурье. Совершенно очевидно, что голограмму Фурье можно получить
только в области дифракции далёкого поля. При этом для выполнения
сразу двух условии
ℓ>a (92)
и
ℓDП<<1 (93)
требуется,
чтобы
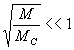 (94)
(94)
т.е.
значение геометрического параметра М должно быть очень малым
сравнительно с МС: в пределе М» 0 или
1+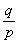 =0
=0
откуда
p
= -q (95)
Это
значит, что предметный пучок должен быть сходящимся. Возникает
хорошо известная схема получения голограммы Фурье (рис.9).
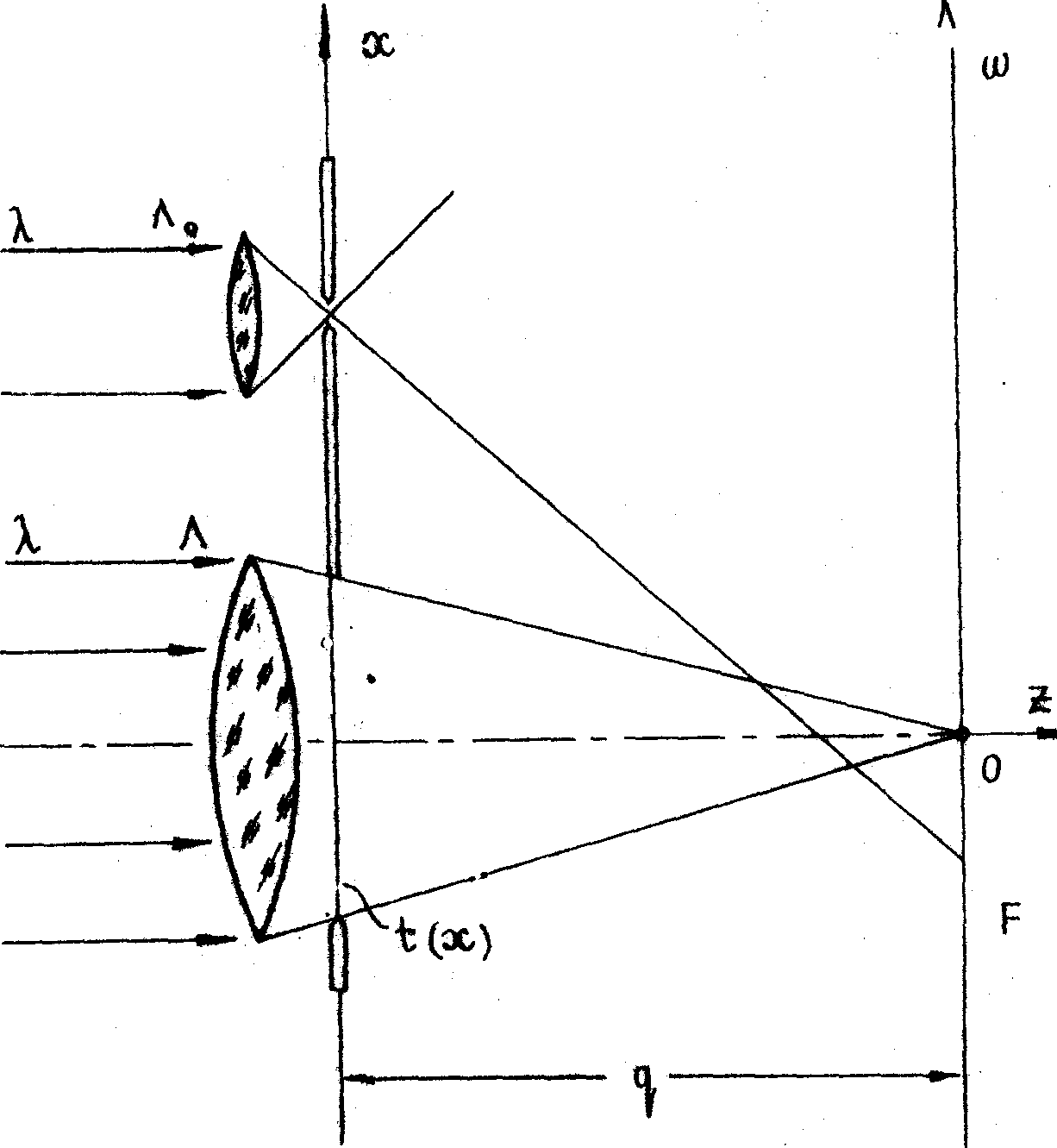
Рис.9.
Схема получения голограммы Фурье при использовании расходящегося
опорного и сходящегося предметного пучков:
Л0
- линза, формирующая опорный пучок (р0 =
0);
Л
- линза, осуществляющая преобразовало Фурье (р = -q).

