|
|
 |
 |

|
| |
- 466 -
ВЛИЯНИЕ ПАРАМЕТРОВ ИСТОЧНИКОВ ИЗЛУЧЕНИЯ НА ГОЛОГРАММУ
Д.И.Стаселько
Известно, что когерентность источника излучения является одним из основных факторов, влияющих на качество изображения, реконструированного голограммой . При этом временная когерентность определяет допустимую глубину голографируемой сцены (см., например, /1/), а пространственная - качество изображения в поперечном направлении (см., например, /2/). В настоящем докладе приводится теория, позволяющая установить функциональную связь между когерентностью источника и качеством реконструированного изображения, а также ряд экспериментальных результатов по получению голограмм при различных режимах работы импульсного источника излучения.
Рассмотрим сначала влияние временной когерентности источника на основании данных, полученных с помощью экспериментальной установки, изображённой на рис.1. Излучение импульсного источника И делилось полупрозрачным зеркалом З 1 на два луча. Сигнальный луч СЛ, расширенный в горизонтальной плоскости цилиндрическим телескопом ЦТ, падал на диффузный белый экран ДЭ под небольшим углом a
(a
»
1°) и, последовательно отражаясь от зеркал З2 и З3, расположенных приблизительно параллельно друг другу, прочерчивал на экране светящуюся траекторию. Излучение, рассеянное экраном, регистрировалось фотопластинкой Г, которая располагалась параллельно плоскости экрана. Референтный луч РЛ, отмененный зеркалом З1, падал на пластинку под углом j
=15° к нормали. Размеры экрана (16х16 см) и его расстояние до голограммы (100 см) обеспечивали с точностью до 3 мм равенство оптических путей от точек голограммы до любой из точек экрана. Точка экрана О соответствовала нулевой разности хода между сигнальным и референтным лучами. Таким образом, цуги волн, приходящие к голограмме
- 467 -
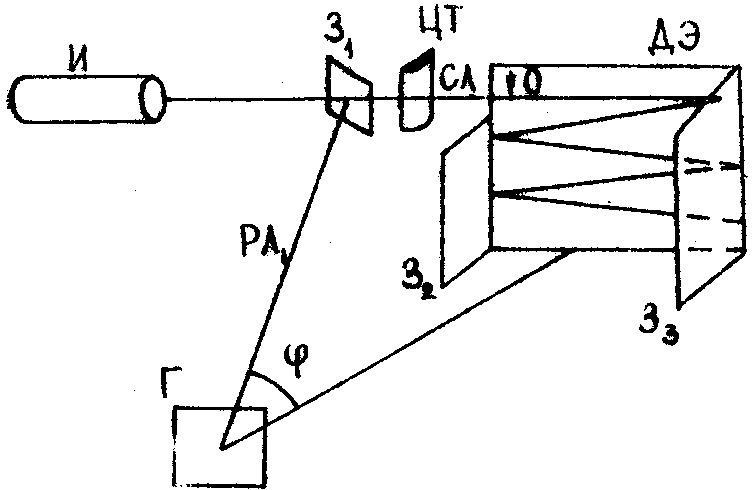
Рис.1.
от различных точек экрана, задерживались относительно референтного луча на временные интервалы, равные времени пробега сигнального луча вдоль экрана, начиная от точки О. Выбранные нами объект (диффузный экран) и расположение элементов схемы позволили создать непрерывное изменение оптической разности хода в значительных пределах при небольших размерах установки, а также упростили интерпретацию экспериментальных результатов и их теоретический анализ.
Объектом исследования служил одномодовый рубиновый лазер, генерировавший одну или несколько продольных мод. Голограммы записывались на фотопластинках "Микрат ВР-2". При этом интенсивность референтного луча в 30¸
50 раз превосходила интенсивность излучения, рассеянного экраном, что обеспечивало работу эмульсии на линейном участке характеристической кривой, наклон которой был равен 1,8. Одновременно с записью голограмм обычным фотоаппаратом снималось распределение интенсивности излучения в плоскости экрана, а на интерферометре Фабри-Перо с базой 2 мм регистрировался спектр источника. Реконструкция голограмм производилась с помощью Не-Nе газового лазера на длине волны 6328 Å.
На рис.2 представлены фотографии реконструированных мнимых изображений траектории луча на экране и соответствующие им интерферограммы Фабри-Перо. На рис.2а показан случай генерации
- 468 -
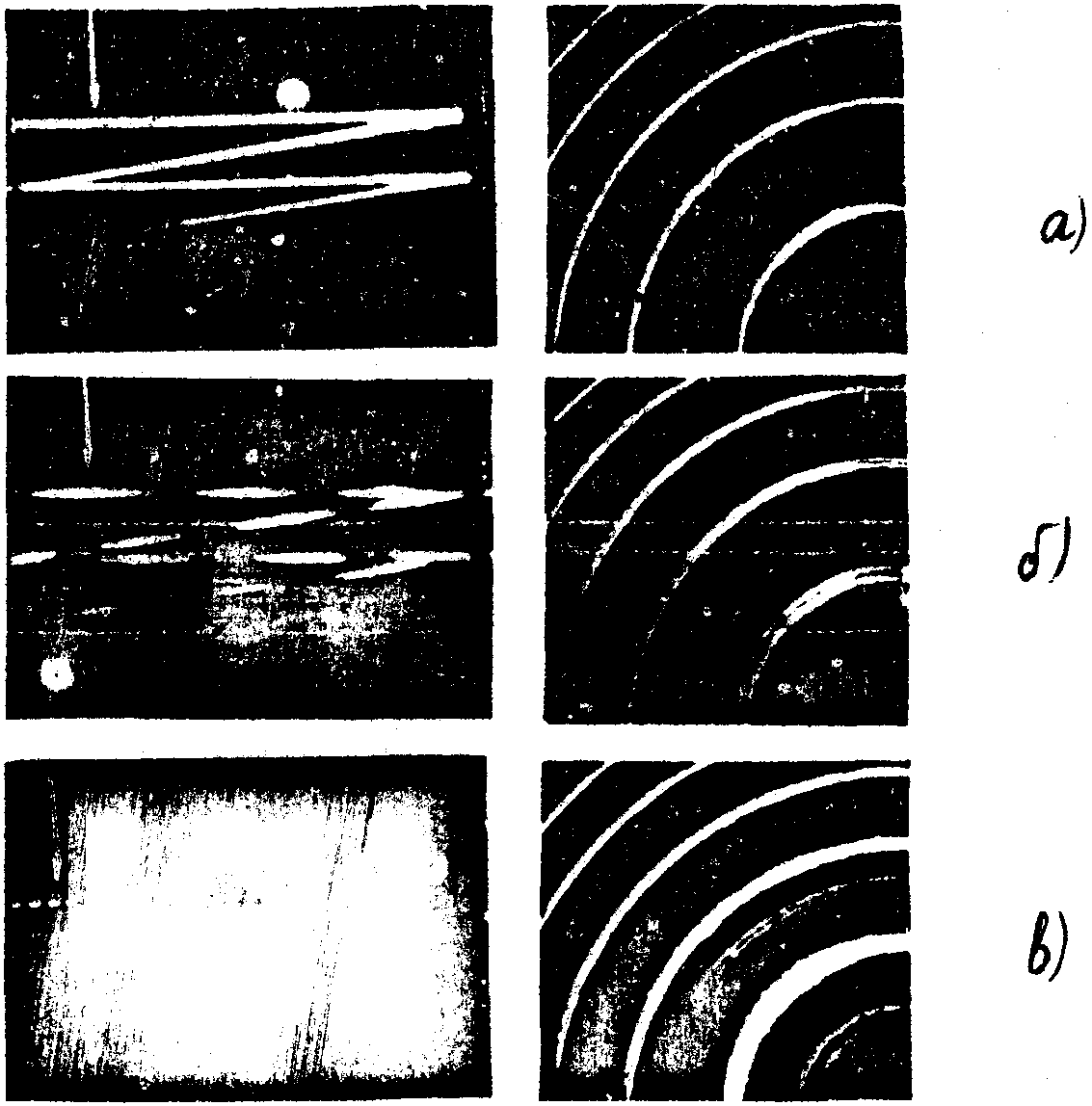
Рис.2.
одной продольной моды в режиме модуляции добротности. Ширина спектра при этом ограничивалась длительностью импульса (~40 нсек по уровню половинной мощности) составляла 0,0005 Å, что соответствовало длине когерентности, равной ~10 м. Как видно на рисунке 2а, изображение не имело разрывов по всей длине траектории, равной 0,7 м (точка О отмечена на фотографии стрелкой). При генерации двух или большего числа продольных мод изображение пересекалось регулярными тёмными полосами, периоды которых совпадали с длинами когерентности Lk, рассчитанными по данным интерферограмм с помощью формулы
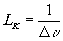
где D
u
- частотный интервал между соответствующими парами линий, выраженный в обратных сантиметрах. Рис.2б иллюстрирует случай
- 469 -
генерации двух гигантских импульсов, когда лазер излучал две продольные моды с отношением интенсивностей 5:3, разделенные частотным интервалом в 0,2 см . Расчётная длина когерентности в этом случае составляла 5 см, что и наблюдалось на рис.2б. Рисунок 2в изображает случай большого числа продольных мод при работе источника в режиме свободной генерации, кодовая структура в этом случае задавалась резонансным отражателем, состоявшим из двух стеклянных пластинок с оптической толщиной Lст=2,5 мм, разделенных воздушным промежутком Lв=25 мм. В соответствии с этим на рис.2в наблюдается регулярное изменение яркости изображения с периодами: L1=2×
Lст=5 мм и L2=2×
Lв=50 мм.
Для интерпретации полученных экспериментальных данных установим функциональную зависимость между распределением яркости реконструированного изображения объекта и временной когерентностью источника. Теоретический анализ процесса записи и реконструкции голограммы проведём в скалярном приближении применительно к схеме, изображённой на рис.1. Значения, которые принимает волновая функция излучения, рассеянного экраном, в плоскости самого экрана y
э, а также значения волновой функции референтного луча в плоскости голограммы y
r представим в виде разложения в интеграл Фурье по частотам:
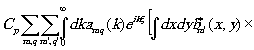 (1) (1)
F
(x,h
,k) = ao(x
)eik[x
+D
(x
)] (2)
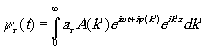 (3) (3)
где k=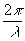 - волновое число, А(k)еij
k -
распределение амплитуд и фаз в спектре
источника излучения, æ
и h -
координаты точек экрана, zo
- расстояние между экраном и голограммой,
h =¦
(æ,h
) -
- волновое число, А(k)еij
k -
распределение амплитуд и фаз в спектре
источника излучения, æ
и h -
координаты точек экрана, zo
- расстояние между экраном и голограммой,
h =¦
(æ,h
) -
- 470 -
расстояние, пробегаемое лучом по экрану (отсчитывается от точки
О, соответствующей нулевой разности хода по отношению к референтному лучу);
аo(x
) и D
(x )
- функции,
описывающие соответственно распределения
амплитуд и фаз на экране с учётом диффузного характера экрана, а также неоднородности
распределения амплитуды и фазы по сечению пучка источника; ar
- амплитуда референтного луча. В выражении
(3) предполагается, что референтный луч
представляет собой плоскую волну, падающую по нормали к голограмме, а фазовый
член 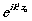 появляется из условия равенства оптических путей референтного и объектного луча,
рассеянного точкой О(x
=0), поскольку последний при распространении
от экрана до голограммы проходит дополнительный оптический путь, равный
zo. Значения волнового поля
излучения, рассеянного экраном, в плоскости голограммы y
о найдём с помощью формулы Кирхгофа, применяя её к каждой монохроматической
компоненте по отдельности и интегрируя полученный результат по спектру
появляется из условия равенства оптических путей референтного и объектного луча,
рассеянного точкой О(x
=0), поскольку последний при распространении
от экрана до голограммы проходит дополнительный оптический путь, равный
zo. Значения волнового поля
излучения, рассеянного экраном, в плоскости голограммы y
о найдём с помощью формулы Кирхгофа, применяя её к каждой монохроматической
компоненте по отдельности и интегрируя полученный результат по спектру
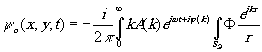
dædh
(4)
Здесь х и у - координаты точек в плоскости голограммы, r радиус-вектор, соединяющий точки голограммы и экрана. Интегрирование ведётся по площади экрана SЭ, освещённой источником. В приближении zo>>æ,h
формула (4) может быть представлена в виде преобразования Фурье:
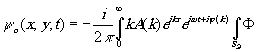 x x
x exp[-ik(xæ+yh
)/R]dædh
(5)
где 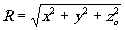 . .
Распределение энергии, воздействующей на фотопластинку за время экспонирования, находим, складывая y
o и y
r, умножая на комплексно-сопряжённое выражение и производя интегрирование по времени в пределах от -¥
и до +¥
:
- 471 -
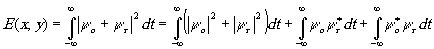 (6) (6)
Ограничимся в (6) рассмотрением второго члена, соответствующего мнимому изображению. Подставляя в него значения y
о и y
r согласно (5) и (3), получаем:
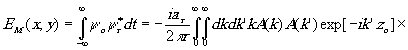

exp[ik(xæ+yh
)/R]dædh 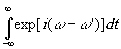 (7) (7)
Учитывая, что интеграл по времени представляет собой дельта-функцию 2p
d
(k-k'), упрощаем (7) до
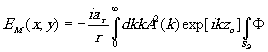
exp[ik(xæ+yh
)/R]dædh
(8)
Считая, что амплитудное пропускание проявленной фотопластинки пропорционально воздействовавшей на неё энергии, а реконструкция производится плоской монохроматической волной y
с=асеxp[iw
ot], падающей по нормали к голограмме, находим волновую функцию реконструированного поля в плоскости голограммы:
y
p(x,y,t) = t
(x,y)y
c = a
EM(x,y)acexp(iw
ot) (9)
где a
- множитель пропорциональности, связывающий ЕМ и t
. Волновую функцию излучения, рассеянного голограммой, в точке æ', h
', z' снова выразим с помощью формулы Кирхгофа в приближении z'>>æ',h
', аналогичном сделанному при выводе (5):
- 472 -
y М(æ',h
',z',t)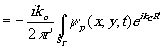 exp[-ikC(xæ+yh
')/R']dædy= exp[-ikC(xæ+yh
')/R']dædy=
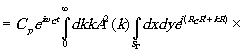 (10) (10)
x exp[-ikC(xæ+yh
')/R']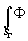 exp[-ik(xæ+yh
')/R']dædh exp[-ik(xæ+yh
')/R']dædh
где 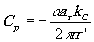 , ,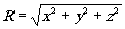
а интегрирование производится по площади голограммы Sг.
Введём теперь условие образования стигматического изображения,
которое математически выражается в том, что при его выполнении интегрирование
в правой части (10)
по координатам х и у, соответствует обратному преобразованию Фурье. Разлагая
R и
R' в ряд по степеням х и у и требуя,
чтобы зависящая от х и у часть разложения kcR'+kR
обращалась в нуль, находим, что условие стигматизма выполняется при
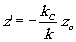 , что
совпадает с результатом, полученным в работе /4/. Таким образом, для каждой
спектральной составляющей изображение фокусируется в плоскости, расположенной
на соответствующем расстоянии от голограммы. Рассмотрим далее образование изображения
в плоскости , что
совпадает с результатом, полученным в работе /4/. Таким образом, для каждой
спектральной составляющей изображение фокусируется в плоскости, расположенной
на соответствующем расстоянии от голограммы. Рассмотрим далее образование изображения
в плоскости 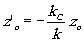 ,
удовлетворяющей условию стигматизма для
спектральной компоненты k=ko
(ko - среднее значение волнового
числа излучения, используемого при записи голограммы). Используя введенное условие
и производя в (10)
необходимые преобразования, получаем для волновой функции в плоскости z'=z'o
следующее выражение: ,
удовлетворяющей условию стигматизма для
спектральной компоненты k=ko
(ko - среднее значение волнового
числа излучения, используемого при записи голограммы). Используя введенное условие
и производя в (10)
необходимые преобразования, получаем для волновой функции в плоскости z'=z'o
следующее выражение:
- 473 -
y M(æ',h
',z'o,t) 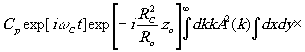
x exp{i[(k-ko)(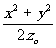 -(xæ+yh
')/R)]o}x -(xæ+yh
')/R)]o}x
x exp[ik(xæ+yh
')/R)]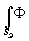 exp[ik(xæ+yh
')/R)]dædh (11) exp[ik(xæ+yh
')/R)]dædh (11)
Согласно (11) при k=ko в плоскости z'o действительно образуется стигматическое изображение объекта. Для других k фазовый член в квадратных скобках не обращается в нуль и определяет расфокусировку в плоскости z'o изображений, соответствующих этим спектральным компонентам. Как показывают проведённые оценки, в условиях эксперимента величина члена в квадратных скобках не превосходила 0,01, что позволяет считать соответствующий экспоненциальный множитель постоянным и равным единице. Учитывая это, а также то, что выполнялось условие ko-k<<ko и, следовательно, множитель k=ko можно вынести за знак интеграла, получаем:
y M(æ',h
',z'o,t) 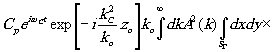
x exp[ik(xæ+yh
')/R)]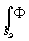 exp[ik(xæ+yh
')/R)]dædh (12) exp[ik(xæ+yh
')/R)]dædh (12)
Выполняя в правой части (12) двойное преобразование Фурье, представляя F
(æ,h
,k) в явном виде, согласно (2), и объединяя все постоянные в комплексном множителе
С 'р
= Cpko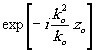 exp[iw
Сt] exp[iw
Сt]
находим окончательное выражение:
- 474 -
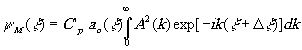 (13) (13)
Нетрудно видеть, что интеграл в правой части выражения (13) является преобразованием Фурье энергетического спектра A2(k) и может рассматриваться поэтому как функция временной когерентности источника g
, выраженная в зависимости от оптической разности хода x
(см., например, /5/):
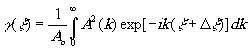 (14) (14)
где 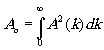 .
С учётом
(14) интенсивность реконструированного
изображения IM
определим как .
С учётом
(14) интенсивность реконструированного
изображения IM
определим как
IM(x
) = |
y
M|
2 = |
C'p|
2a2o(x
)|
g
(x
)|
2 = CIo(x
)|
g
(x
)|
2 (15)
где C=|
C'p|
2А2o - постоянная величина, а Io(x
)=а2o( x
) - освещённость объекта во время экспонирования. Из формулы (15) следует, что яркость реконструированного изображения траектории луча на экране пропорциональна квадрату модуля функции временной когерентности источника. Для проверки соотношения (15) с помощью формулы (14) была рассчитана зависимость |
g
(x
)|2 Для режима, соответствующего рис.2б. Построенная таким образом кривая приведена на рис.5 вместе с нормированным распределением IM(x
)/Io(0), которое было получено экспериментально путём фотометрирования реконструированного изображения. Как видно из рис.5, экспериментальная кривая согласуется с расчётной. Таким образом, при равномерном освещении экрана (Io=const) изображение, реконструированное голограммой, представляет собой не что иное, как "замороженную" картину временной когерентности источника. Одновременно диффузный экран моделирует протяженную по глубине сцену, и из картины, полученной данным методом, легко может быть определена яркость изображения частей объектов, находящихся на различных расстояниях от голограммы.
- 475 -
До сих пор мы рассматривали влияние временной когерентности в предположении, что источник обладает полной пространственной когерентностью. Проанализируем теперь более общий случай, когда излучение источника описывается произвольной функцией пространственно-временной когерентности. При этом предполагаем, что источником излучения является лазер, излучающий набор продольных и поперечных мод в течение ограниченного промежутка времени. Волновую функцию поля излучения в сечении х,у на расстоянии z от источника y
(x,y,z,t) представим как суперпозицию полей отдельных мод, которые запишем виде разложения в интеграл Фурье по частотам
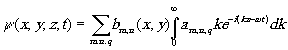 (16) (16)
где m, n
и q -
поперечные и продольные индексы мод, k=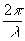 - волновое число, l
-
длина волны излучения. С -
скорость света. В выражении (16)
каждая мода характеризуется амплитудно-фазовым распределением поля в поперечном
направлении bm,n(х,y)
и по спектру am,n,q(k).
Для более чёткого выяснения особенностей
влияния модовой структуры источника на голограмму выберем в качестве объекта
диффузный экран, который располагаем теперь нормально к падающему излучений.
Предположим далее, что на диффузный экран и на голограмму проектируется определённое
сечение пучка излучения, распространяющегося от источника (например, распределение
поля на торце генератора y (х,у,о)).
В соответствии с этим значения, которые
принимает волновая функция излучения, рассеянного экраном, в плоскости самого
экрана y Э,
а также значения волновой функции референтного
луча и плоскости голограммы y
Г
определим следующими выражениями для сокращения записи будем обозначать различные
поперечные моды одним индексом m)
- волновое число, l
-
длина волны излучения. С -
скорость света. В выражении (16)
каждая мода характеризуется амплитудно-фазовым распределением поля в поперечном
направлении bm,n(х,y)
и по спектру am,n,q(k).
Для более чёткого выяснения особенностей
влияния модовой структуры источника на голограмму выберем в качестве объекта
диффузный экран, который располагаем теперь нормально к падающему излучений.
Предположим далее, что на диффузный экран и на голограмму проектируется определённое
сечение пучка излучения, распространяющегося от источника (например, распределение
поля на торце генератора y (х,у,о)).
В соответствии с этим значения, которые
принимает волновая функция излучения, рассеянного экраном, в плоскости самого
экрана y Э,
а также значения волновой функции референтного
луча и плоскости голограммы y
Г
определим следующими выражениями для сокращения записи будем обозначать различные
поперечные моды одним индексом m)
y Э(æ,h
,zЭ,t)=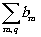 (æ,h
) (æ,h
)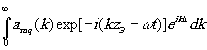 (17) (17)
- 476 -
y Г(æ,h
,zГ,t)=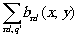 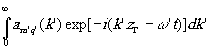 (18) (18)
где остальные обозначения те же, что и в выражениях (1)-(3). Опуская далее операции, описываемые формулами (4)-(11), приведём выражение, определяющее значения реконструированной волновой функции в плоскости фокусировки мнимого изображения экрана:
y Г(æ,h
,zГ,t)=
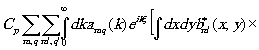 (19) (19)
х exp[ik(xæ'+yh
')/R]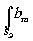 (æ,h
)eikD exp[-ik(xæ+yh
)/R]dædh (æ,h
)eikD exp[-ik(xæ+yh
)/R]dædh
где Cp - комплексный постоянный множитель, x
=zЭ-zГ-zo - разность хода между сигнальным и референтным пучками, а интегрирование производится по площади голограммы SГ, освещаемой при реконструкции.
Рассмотрим вид изображения, реконструированного малой площадкой голограммы, в пределах которой функции b*m'(x,y) остаются постоянными. Это позволяет вынести b*m'(x,y)=const=b*m за знак интеграла и выполнить в правой части выражения (19) двойное преобразование Фурье, что приводит (19) к следующему виду:
y M(æ',h
',z'o)=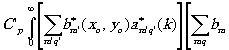 (æ' (æ'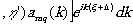 (20)
(координаты xo
и yo
фиксируют положение выбранной области на голограмме). Используя соотношение
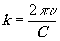 ,
представим (20)
в более привычном виде ,
представим (20)
в более привычном виде
y M(æ',h
',z'o)=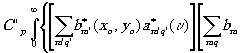 (æ' (æ'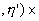
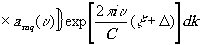
(21)
- 477 -
Согласно выражениям (17) и (18), функции
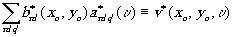
и
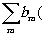
æ'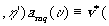 æ' æ'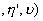
представляют собой спектры колебаний поля источника в точках
хо, уо и æ',
h '. Отсюда
следует, что функция, заключённая в фигурных скобках, имеет смысл взаимной спектральной
плотности колебаний в точках хо, уо и æ',
h ', а
интеграл по u
- смысл ненормированной взаимной функции
когерентности источника Г(хо,уо,æ',h
'); 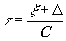 (см., например, /5/). Учитывая это, представим
(21) как
(см., например, /5/). Учитывая это, представим
(21) как
y
М(æ',h
',z'o) = CMГ(хо,уо;æ',h
',t
) (22)
где СМ - постоянная величина. Следует отметить, что функция когерентности, определённая таким образом, описывает как стационарные, так и импульсные источники излучения. Производя стандартную операцию нормировки функции Г(хо,уо;æ',h
',t
), выразим y
М через нормированную функцию взаимной когерентности g
(хо,уо;æ',h
't
).
y
М(æ',h
',z'o) = CM(J(хо,уо)J(æ,h
))1/2g
(хо,уо;æ',h
',t
) (23)
где J(xo,yo) и J(æ,h
) - интенсивности поля в плоскости голограммы и на объекте во время экспозиции. С учётом (23) находим распределение интенсивности в реконструированном изображении JM(æ',h
',z'o):
JM(æ',h
',z'o)=|
y
M(æ',h
',z'o)|
2=C'MJ(æ,h
)|
g
(xo,yo;æ',h
';t
)|
2 (24)
С' M=C M×
J (хo, уo). Таким образом, при наблюдении реконструированного изображения через малую область голограммы с координатами xo,yo видимая яркость изображения оказывается промодулированной квадратом модуля функции пространственно-временной когерентности источника |
g
(хо,уо;æ',h
',t
)|
2. Как известно, функция пространственной когерентности является функцией четырёх координат. В данном случае наблюдается функция пространственной когерентности одной фиксированной точки по отношению ко всем остальным точкам источника,
- 478 -
т.е. функция в зависимости от двух координат ( æ',h
') при фиксированном значении двух других координат (хо,уо). Из формулы (24) непосредственно следует, что, меняя положение точки хоуо (например, путём сканирования пучком, используемым при реконструкции, по площади голограммы), можно определить степень взаимной когерентности между любыми точками источника, т.е. найти "полную" функцию пространственной когерентности в зависимости от всех четырёх координат |
g
(хо,уо,æ',h
't
)|
2. Суммируя полученные результаты, можно сделать вывод о том, что изображения диффузных объектов, создаваемые голограммами, фактически представляют собой портреты пространственно-временной когерентности источников, использовавшихся при записи этих голограмм.
До этого момента мы обсуждали влияние когерентности источника на изображения, наблюдаемые через малые участки голограммы. Рассмотрим теперь влияние кодовой структуры источника на качество голограммного изображения в общем случае, когда область голограммы, освещаемая при реконструкции, имеет произвольные размеры, и вернёмся к выражению (19). Нетрудно видеть, что член, стоящий в квадратных скобках, можно представить как преобразование Фурье от произведения функций
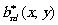
и 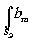 (æ,h
)eikD exp[-ik(xæ+yh
)/R]dædh (æ,h
)eikD exp[-ik(xæ+yh
)/R]dædh
последняя из которых, в свою очередь, является Фурье-образом
функции 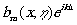 .
Применяя к
(19) формулу Парсеваля, находим, что .
Применяя к
(19) формулу Парсеваля, находим, что
к Функция когерентности, определённая с помощью голограммы, является неполной в том смысле, что она, не содержит информации об относительных фазовых сдвигах различных точек источника. Однако. во многих случаях, в том числе в голографии, это обстоятельство не играет существенной роли.
Отметим также, что результат, подученный в работах /6,7/, является по сути дела частным случаем соотношения /24/, когда хо и уо принимают единственное фиксированное значение.
- 479 -
y M(æ',h
',z'o)=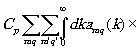
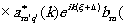
æ'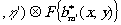 (25) (25)
где значок Ä
означает операцию свёртки, а символ F - преобразование Фурье. Из формулы (25) следует, что влияние многоголовой структуры источника эквивалентно действию аппаратной функции, которая представляет собой преобразование Фурье от распределения поля референтного луча на голограмме. Поэтому изображения точек, создаваемые интерференционными картинами, соответствующими различным поперечным модам, должны совпадать со структурами этих мод в дальней зоне излучения. Таким образом, из анализа выражений (24) и (25) следует, что многомодовый характер генерации приводит к снижению качества изображения, реконструированного голограммой, за счёт падения яркости изображения, ограничения эффективной апертуры голограммы и усложнения структуры точек изображения. Некоторые примеры, демонстрирующие влияние пространственно-временной когерентности источника на голограммное изображение, приведены в работе /3/.
В заключение приведём результаты экспериментов по проверке справедливости соотношения (24). На рис.4б, в представлены фотографии мнимых изображений экрана, снятых по описанному методу через различные точки голограммы, а на рис.4а показано интегральное распределение поля на диффузном экране, полученное путём обычного фотографирования. Источник излучения - рубиновый лазер с модулированной добротностью - работал в режиме генерации многих поперечных мод. Стрелками и цифрами на диффузном экране отмечены области, соответствующие тем, через которые велось наблюдение реконструированного изображения. Видно, что изображения, наблюдаемые через различные точки голограммы значительно отличаются друг от друга и от интегрального распределения поля. При этом наиболее яркими в реконструированном изображении видны точки, соответствующие
- 480 -
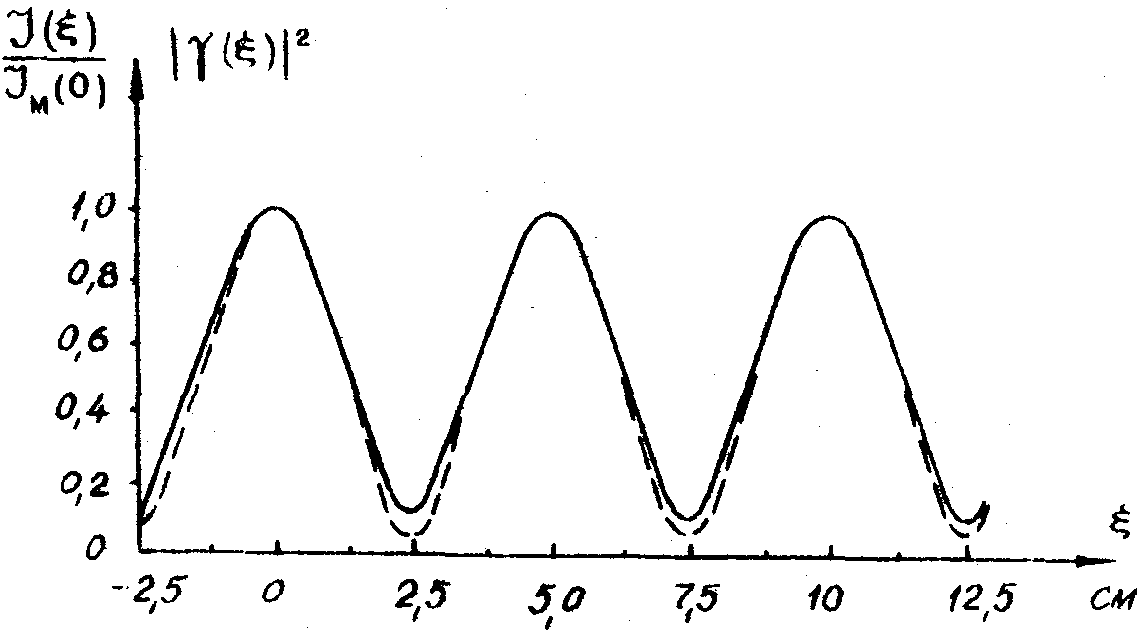
Рис.3.

Рис. 4.
- 481 -
тем, через которые велось наблюдение, что находится в полном соответствии с теорией, поскольку степень когерентности точки источника по отношению к самой себе всегда максимальна. При работе лазера в одномодовом режиме распределение яркости в реконструированном изображении не зависело от точки наблюдения и совпадало с интегральным распределением на обычной фотографии. Эти результаты, наряду с приведёнными выше, показывают, что когерентные свойства источников излучения (в том числе импульсных) раскрываются при помощи голограммы с большой детальностью и полнотой .
Основные выводы из проделанной работы могут быть сформулированы следующим образом:
1. Изображения диффузных объектов, реконструированные голограммами, представляют собой портреты пространственно-временной когерентности источников, использовавшихся при записи голограмм, и могут быть применены для детального и полного исследования когерентных свойств источников.
2. При записи голограмм с помощью многомодового источника распределение поля в реконструированном изображении определяется как свёртка распределения поля на объекте с Фурье-преобразованием модовой структуры источника, проектируемой референтным лучом на голограмму.
- 482 -
Литература
1. Ю.Н.Денисюк. Оптика и спектроскопия, 25, 522 (1963).
2. Ю.Н.Денисюк. Журнал научной и прикладной фотографии и кинематографии, 11, 46 (1966).
3. Д.И.Стаселько, А.Г.Смирнов, Ю.Н.Денисюк. Оптика и спектроскопия, 25, №6 (1968).
4. R.Meier. JOSA, 55, 987 (1965).
5. M.Born, E.Wolf. Pr1nciples of Optics, 3rd. ed. , 1965.
6. M.Lurie. JOSA, 56, (1966).
7. M.Lurie. JOSA, 58, 614 (1968).
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

