|
|
 |
 |

|
| |
- 414 -
РЕАКТИВНЫЙ МЕТОД РЕКОНСТРУКЦИИ ГОЛОГРАММ И ОПТИЧЕСКОЙ ФИЛЬТРАЦИИ
Г.А.Соболев
Работа устройств оптической согласованной фильтрации связана с необходимостью регистрации низких уровней освещённости в световом пятне корреляционной функции на выходной плоскости устройства. Особые трудности возникают при ведении фильтрации в наиболее интересном случае быстроменяющейся ситуации. Прямые методы, связанные с повышением мощности лазера или чувствительности приёмного устройства, не всегда целесообразно использовать из-за усложнения аппаратуры и возможного повышения инерционности. Одна из возможностей преодоления указанных затруднений при оптической согласованной фильтрации связана с помещением транспаранта или голограммы-фильтра внутри резонатора. При этом часть энергии, падающей на транспарант, которая в обычных условиях не используется и безвозвратно теряется, поступая в нулевой порядок дифракции, возвращается в резонатор. Поскольку транспарант имеет формальную аналогию с реактивным элементом в радиотехнике процесс получил наименование реактивной обработки информации /1,2/ Такая возможность была предложена для решения задач голографической технологии /3/, однако очевидно, что аналогичный принцип может быть использован для оптической обработки информации.
1 Требования к резонаторам
Функционирование оптического коррелятора с внутрирезонаторным объектом существенно определяется конструкцией резонатора. Поскольку решение задачи о колебаниях открытого резонатора в общем виде для зеркал произвольной формы затруднительно, привлекаются добавочные предположения о малости длины волны по сравнению с размерами резонатора и несущественном возмущении распределения поля в генерирующем резонаторе вводимыми в него объектами
- 415 --
(в том числе голограммами). Такие предположения позволяют привлечь принцип Гюйгенса в формулировке Френеля-Кирхгофа для расчёта полей на зеркалах и внутри резонатора. Поле на одном зеркале U2 в зависимости от поля на другом U1 может быть выражено через поверхностный интеграл
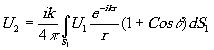 (1) (1)
(r - расстояние от одного
зеркала до пробной точки, q
- угол между Т и 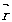 нормалью к зеркалу в соответствующей точке). В общем случае поля у обоих зеркал
связаны парой интегральных уравнений:
нормалью к зеркалу в соответствующей точке). В общем случае поля у обоих зеркал
связаны парой интегральных уравнений:
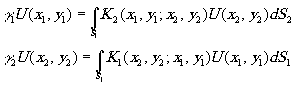 (2) (2)
(g
1, g
2 - постоянные распространения, определяющие затухание и фазовый сдвиг волны при распространении от одного зеркала к другому; S - функция, определяющая форму зеркала; ядра К1 и К2 зависят от геометрии зеркала). Для сферических зеркал (если не учитывать для простоты отсутствие осевой симметрии у голограмм с внеосевым опорным пучком) можно разделить интегральные уравнения и свести их к одномерным, допускающим численное, реже аналитическое, решение:
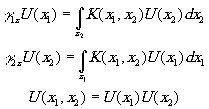 (3) (3)
Ядро уравнения (3) для прямоугольных зеркал имеет вид:
- 416 -
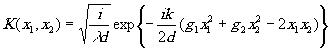 (4) (4)
(d - расстояние между
зеркалами; R1, R2
- их радиусы кривизны;
g1=1-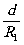 и g2=1-
и g2=1-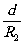 - параметры; для стабильного резонатора
0<g1g2<1).
Для круглых зеркал с синусоидальным азимутальным
полем U(r,j
)=Rℓ(r)e-jℓF
одномерные интегральные уравнения в цилиндрических координатах будут:
- параметры; для стабильного резонатора
0<g1g2<1).
Для круглых зеркал с синусоидальным азимутальным
полем U(r,j
)=Rℓ(r)e-jℓF
одномерные интегральные уравнения в цилиндрических координатах будут:
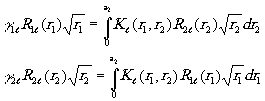
с ядром
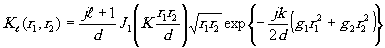 (5) (5)
( Jℓ - функция Бесселя -порядка, первого рода; а1, a 2 - радиусы зеркал). Для случая произвольной конфигурации одного из зеркал (например, голографическое зеркало с большой глубиной рельефа, приводящей к возмущению мод резонатора) даже при плоской или сферической конфигурации другого зеркала трудно рассчитывать на возможность нахождения какого-либо аналитического решения интегральных уравнений типа (5). Для упрощения задачи целесообразно наложить на функцию формы S(x2,y2) ряд ограничений, которые определят и требования, предъявляемые к голографическому зеркалу:
- пространственная частота S(x2,y2) достаточно высока, так что свет, дифрагировавший на голографическом зеркале, выводится из резонатора;
- глубина рельефа на голограмме мала по сравнению с длиной волны (z2<<l
) - поверхность достаточно гладкая, голографическое зеркало не оказывает значительного возмущения на моды резонатора;
- 417 -
- двумерная функция может быть представлена в виде суммы одномерных S2(x2,y2)=S'(х2)+S"(у2).
Эти упрощения сведут аналитическое выражение для голографического зеркала к выражению для зеркала простейшей геометрической формы, вокруг которой осциллирует поверхность голограммы, а интегральные уравнения для резонатора с голографическим зеркалом - к интегральным уравнениям для резонаторов с простейшими зеркалами, для которых имеются в литературе аналитические или численные решения. В работе /2/ рассмотрен случай фазового объекта, расположенного в плоскости симметрии резонатора с сопряженными плоскими полями. Интегральное уравнение имеет вид:
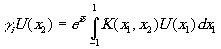 (6) (6)
с ядром
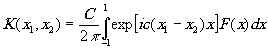 (7) (7)
{d =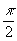 -2k¦
- -2k¦
- геометрический фазовый сдвиг;
¦ - фокусное
расстояние линзы внутри резонатора; С=2p N.
С£ d
- для одномодового режима, N
- число Френеля; F(х)=ℓiA(x)
- фазовый объект). Показано, что моды
резонатора с объектом совпадают с модами, собственные функции со сфероидальными
волновыми функциями невозмущённого резонатора, если объект чисто фазовый
(F(x)=eiG(x)Cosw
(x)x; |G(x)|£ 0,2; G(х),
w (x)
- узкополосные), а полезная информация
выводится из резонатора (w достаточно высока).
Поскольку собственные функции интегральных уравнений дают поперечное распределение
поля в резонаторе, то они представляют интерес при изучении разрешения, достигаемого
при реконструкции голограмм. известно, что в системе с прямоугольными координатами
поле в поперечном сечении резонатора имеет вид:
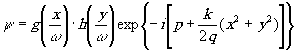 (8) (8)
- 418 -
где параметр р опивает комплексный сдвиг фазы при распространении пучка вдоль резонатора, параметр q(z) - изменение интенсивности по сечению пучка, причём g×
h выражается через полиномы Эрмита тип порядка (Лаггера для круглых зеркал):
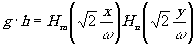 (9) (9)
Простейшее распределение имеет место для m=n=0 (Но=1) и соответствует гауссову распределению в одномодовом резонаторе. При обращении голограммы, фильтра или транспаранта таким пучком может бить достигнуто максимальное разрешение в изображении. Для случая реконструкции голограмм, двумерного спектрального анализа или в трансформирующем сечении многоканального спектроанализатора гауссово (неоднородное) распределение даже удобно, поскольку может привести к низкому уровню боковых лепестков для точечного объекта. Использование гауссова распределения для освещения транспаранта с объектом при оптической согласованной фильтрации вне резонатора представляет некоторые неудобства, так как связано с использованием лишь центральной достаточно однородной части пучка. Однако в случае объекта внутри резонатора использование центральной части пучка может быть не связано с потерей мощности, возвращаемой снова в резонатор.
Многомодовое распределение нежелательно в оптических резонаторах, осуществляющих оптическую согласованную фильтрацию, и необходимо использовать селекцию типов колебаний. Однако для достаточно малых объектов фильтрация, вероятно, осуществима и при многомодовом режиме работы лазера. Исследование такой возможности особенно интересно для многомодовых твёрдотельных лазеров (например, при изучении распределения аэрозолей и других микрообъектов по размерам). Многомодовый режим допустим также в некоторых случаях реактивной реконструкции голограмм.
- 419 -.
2. Энергетика метода
Представляет интерес оценка энергетического выигрыша, достигаемого при внутрирезонаторной обработке оптической информации. Пусть энергетический выигрыш
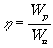 (10) (10)
( Wp
- плотность энергии светового лучка,
наступающая в изображение или в некоторый частотный интервал его спектра при
помещении объекта внутри резонатора; Wn
- аналогичная плотность при пассивном
освещении объекта -
фазового транспаранта или голограммы). В общем случае
Wp
и Wn
полностью определяются плотностью энергии, соответственно существующей в резонаторе
или падающей на объект вне резонатора. Для идеального фазового объекта без потерь,
не возмущающего поля в резонаторе, выигрыш 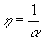 ,
где
a - дифракционная
эффективность объекта. Такой идеальный объект-транспарант, голограмма или голографическое
зеркало (рисунки 1а,б) будет выводить из резонатора ОКГ ту же энергию, что и
оптимально подобранное обычное зеркало резонатора. Поскольку при связи через
окна резонатора можно использовать ,
где
a - дифракционная
эффективность объекта. Такой идеальный объект-транспарант, голограмма или голографическое
зеркало (рисунки 1а,б) будет выводить из резонатора ОКГ ту же энергию, что и
оптимально подобранное обычное зеркало резонатора. Поскольку при связи через
окна резонатора можно использовать 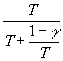 часть от
энергии внутри резонатора, а при дифракционной связи
часть от
энергии внутри резонатора, а при дифракционной связи
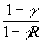 , где
1-g -
дифракционные потери на проход; Т, R
– коэффициенты
прозрачности и отражения окон, то достижимая
эффективность будет , где
1-g -
дифракционные потери на проход; Т, R
– коэффициенты
прозрачности и отражения окон, то достижимая
эффективность будет
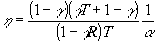 (11) (11)
или
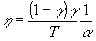 , ( , (
если
R» 1, T<<1) (12)
Реальный фазовый объект, голограмма, находящиеся внутри резонатора вносят в резонатор потери, которые ухудшают добротность резонатора и ограничивают практически достижимый выигрыш.
- 420 -
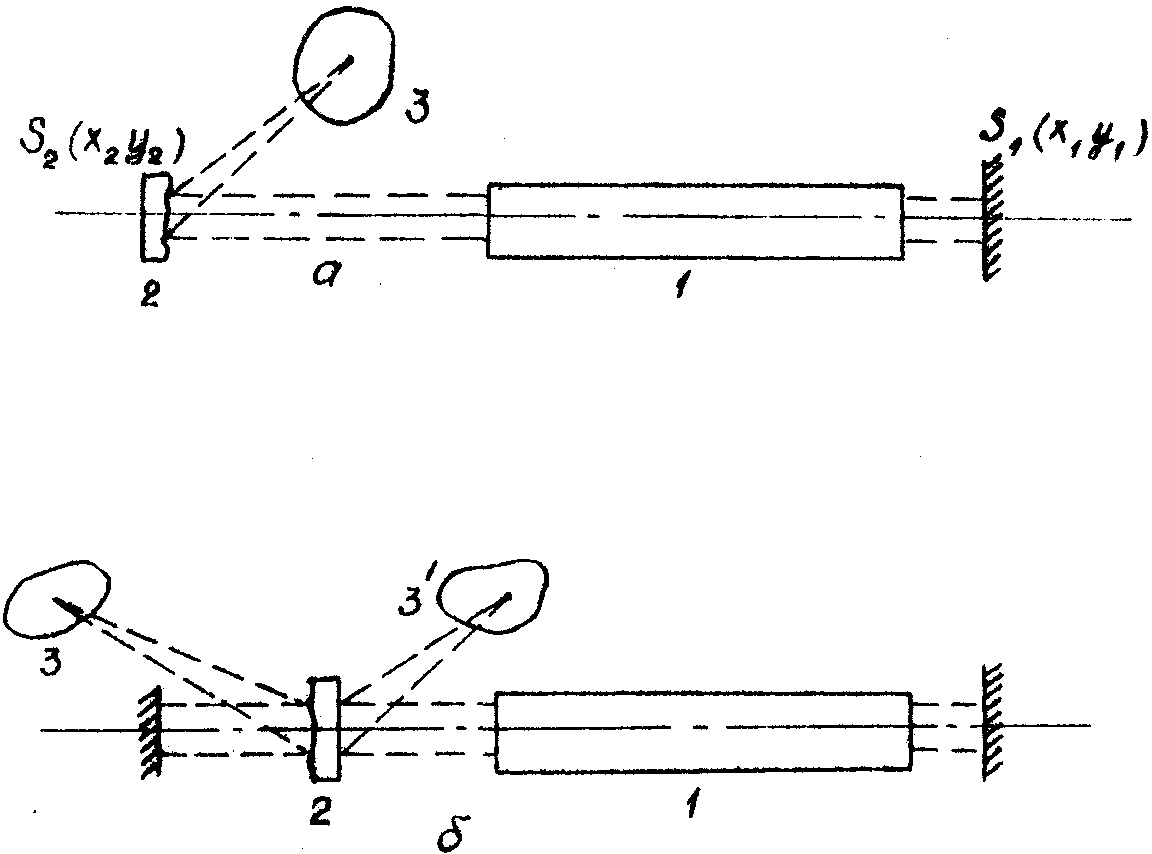
Рис.1. Схема реактивной реконструкции:
1 - активное вещество;
2 - голограмма или голографическое зеркало;
3 - изображение.
3. Конструкция реактивных оптических корреляторов
Для выполнения реактивной фильтрации необходимо отделить излучение, дифрагировавшее на объекте и несущее полезную информацию, от остального излучения. Первое должно пройти через голограмму-фильтр, установленную в пространственно-частотной плоскости по отношению к объекту, второе должно быть перехвачено зеркалом резонатора. Это легко осуществить, если информативные пространственные частоты объекта достаточно высоки. Разделение легко осуществляется в резонаторах с линзовыми элементами. Возможный
- 421 -
вариант коррелятора, показан на рис.2а (фильтр установлен в плоскости зеркала, причём центральная металлизированная часть фильтра является зеркалом ОКГ).
Для уменьшения числа поверхностей, вносящих потери, фазовый объект может помещаться непосредственно на поверхность линзового элемента, а линзовые элементы могут быть совмещены с активным веществом (как это имеет место в сопряжённом концентрическом резонаторе). На рис.2б приведена возможная схема оптического коррелятора, использующего резонатор с плоскими зеркалами.
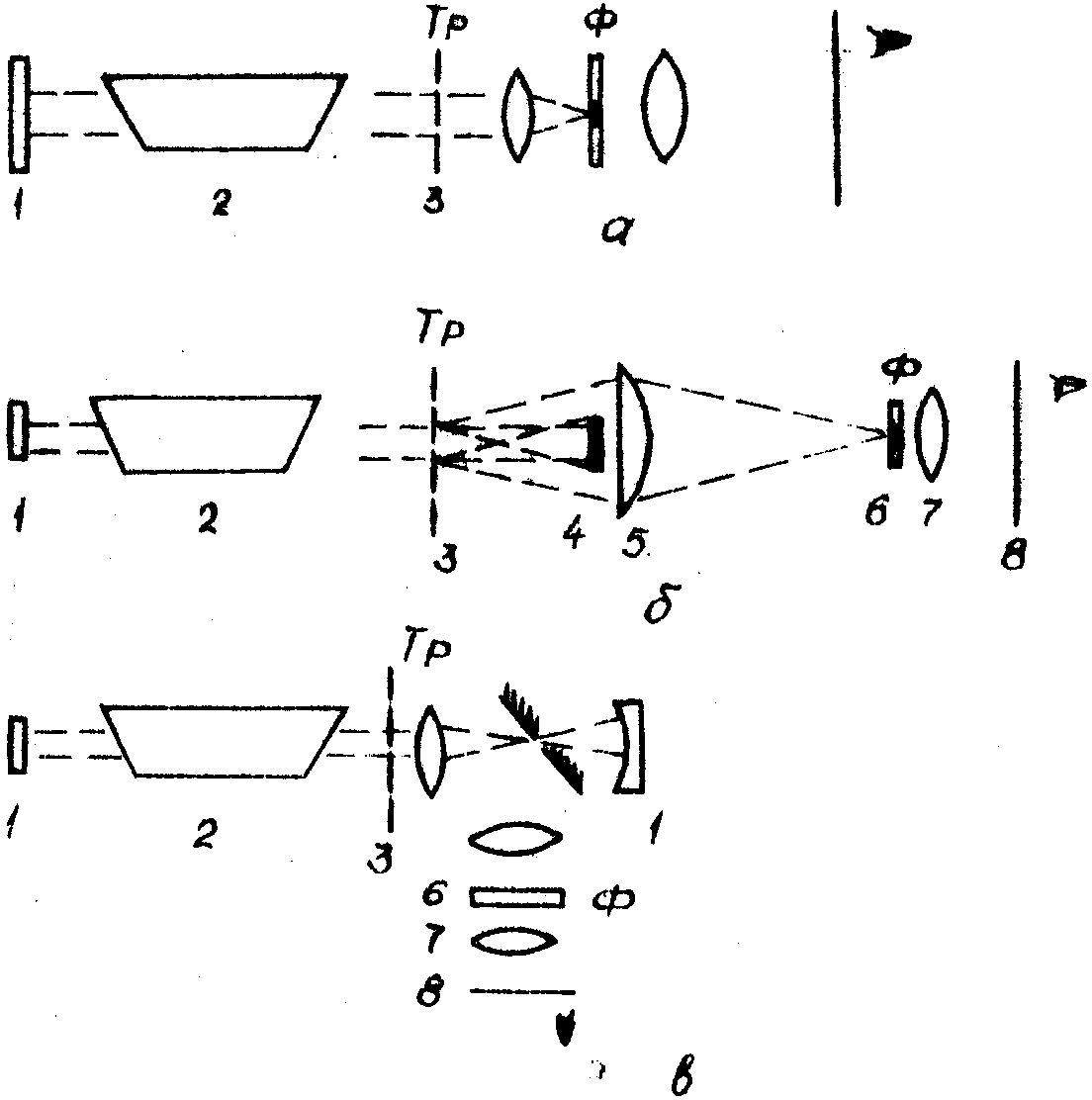
Рис.2. Корреляторы:
1 - зеркало; 2 - активное вещество; 3 - транспарант; 4 - зеркало; 5 - компенсирующая линза; 6 - фильтр; 7 - линза; 8 - выходная плоскость.
- 422 -
Компенсирующая линза 5 фокусирует плоские световые пучки, дифрагировавшие на объекте в плоскости, где расположен фильтр 6. Вероятно, по близкой схеме могут быть реализованы и другие аналогичные системы оптических когерентных корреляторов (например, схема с освещением транспаранта сходящейся световой волной, в фокусе которой вне резонатора расположен фильтр). При рассмотрении конструкций корреляторов удобно оперировать с эквифазными поверхностями в резонаторе со сферическими зеркалами, учитывая ширину пятна минимального диаметра, где следует устанавливать зеркало лазера, и радиус кривизны волны, падающей на фазовый транспарант, обуславливающей положение спектральной плоскости и необходимость применения компенсирующей линзы. Для исключения неоднородного освещения транспаранта целесообразно использовать фильтр, например в виде зеркала с отверстием, установленным в фокусе линзы (рис.2в). Вероятно, для минимизации потерь допустимо введение транспаранта на стекле, расположенном под углом Брюстера, например на окне ячейки с активным веществом. Для сохранения генерации необходимо, чтобы потери были скомпенсированы усилением активной среды, что заставляет использовать активную среду с достаточно высоким усилением.
4. Экспериментальное исследование реактивной схемы фильтрации и реконструкции голограмм
Экспериментально проверялась возможность осуществления оптической согласованной фильтрации при помещении фазового, транспаранта внутрь резонатора лазера на ионизованной Hg (l
=6150Å) и использования оптического согласованного фильтра в качестве зеркала резонатора. Схема установки приведена на рис.5. Плоское зеркало резонатора изготавливалось из фильтров, полученных при обычной методике /4/ следующим образом: из центра фильтра аккуратно удалялся небольшой (2х2 мм2) участок эмульсии, а на очищенный участок поверхности напылялся в вакууме тонкий слой серебра, образующий достаточно высококачественное отражающее покрытие для второго зеркала резонатора, близкого к полуконцентрическому.
- 423 -
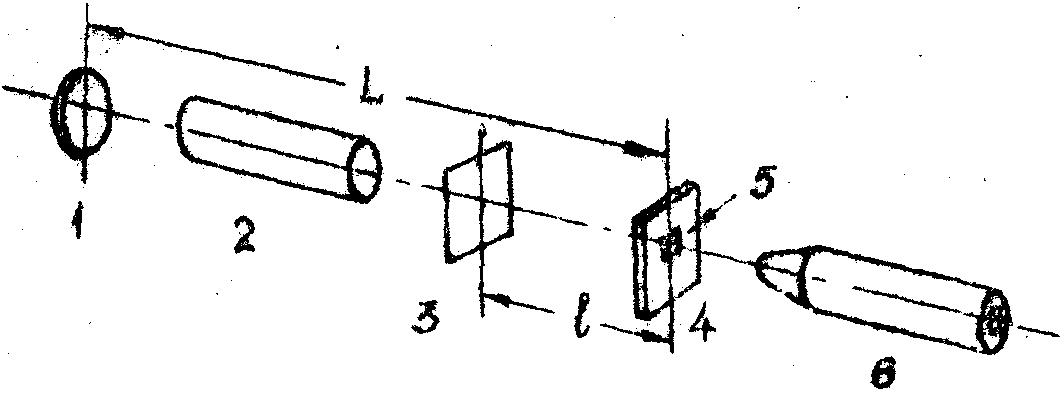
Рис.3. Схема экспериментальной установки:
1 - зеркало; 2 - трубка ОКГ на Нg; 3 - транспарант; 4 - фильтр, 5 - отражающее покрытие; 6 - зрительная труба.
Объектом для фильтрации служил негатив цифровой таблицы /4/. Корреляционный сигнал в виде достаточно яркой точки наблюдался только при существенном ограничении апертуры резонатора, что обусловлено приближением к одномодовому режиму.
Проводились также исследования возможности реактивной реконструкции голограмм. Результаты подобных исследований описаны в ряде работ /3,5/ и др. На рис.4 приведена схема импульсного лазера на рубине 2 с голографическим зеркалом 3. Реконструированное изображение фокусировалось на обрабатываемый материал, в котором пробивались отверстия. Указанный эксперимент подтверждает перспективность метода для решения задач голографической технологии /2/.
- 424 -
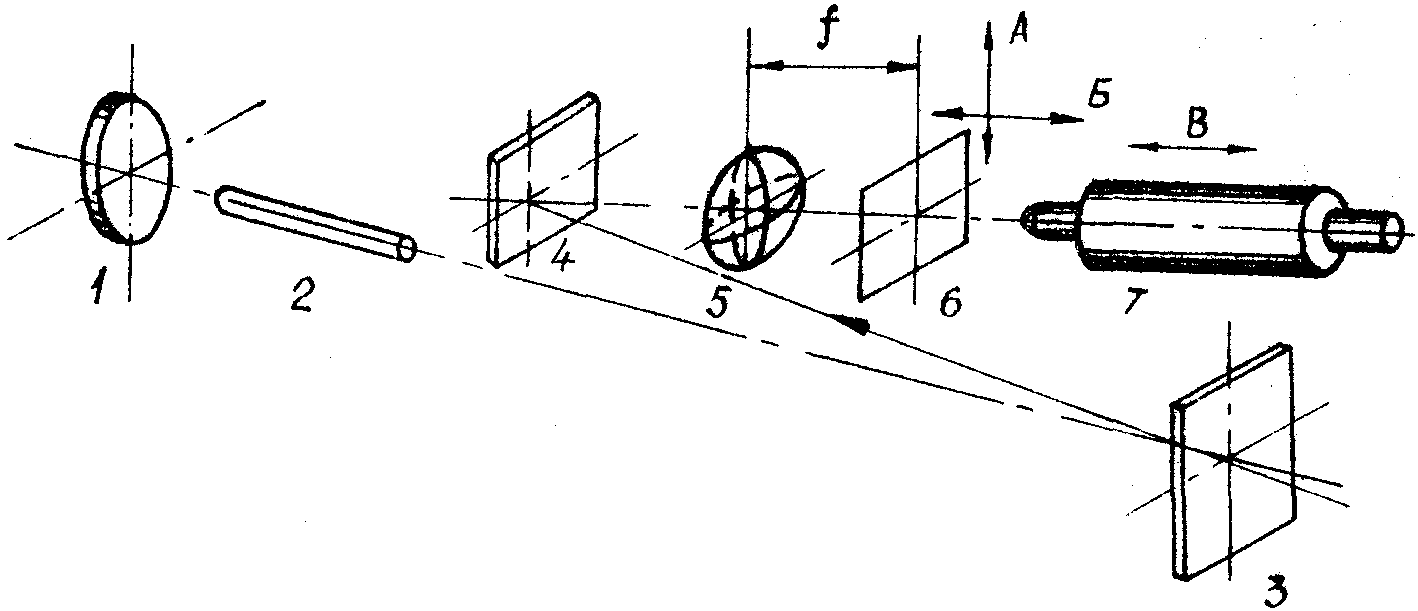
Рис.4 . Схема экспериментальной установки:
1 - зеркало ОКГ; 2 - рубиновый стержень; 3 - голографическое зеркало; 4 - поворотное зеркало; 5 - линза; 6 - обрабатываемый материал; 7 - юстировочный микроскоп.
5. Приложения метода, реактивной реконструкции голограмм и обработки информации
Рассмотренная теория резонатора с фазовым объектом и соответствующие эксперименты позволяют сделать заключение о возможности применения подобных схем с некоторыми изменениями при оптической согласованной фильтрации. Строго такая возможность следует из наличия в рассмотренных системах двух плоскостей, между распределением амплитуд светового поля, в которых имеет место преобразование Фурье. Этот факт обуславливает возможность осуществления на основе принципа реактивной реконструкции многочисленной гаммы устройств когерентно-оптической обработки информации. К ним следует. отнести устройства, служащие для реконструкции голограмм /1,2,5/, визуализации информации с термопластической плёнки и телевизионной системы Эйдофор /1,2,5/, визуализации
- 425 -
воздушных потоков /2/ . Однако следует указать и на возможность осуществления на основе этих принципов устройств, обеспечивающих выполнение вычислительных операций: спектроанализаторов, корреляторов в пространственной и частотной плоскостях, в том числе двумерных и многоканальных. В зависимости от требуемых характеристик (разрешения, количества каналов, динамического диапазона) такие устройства могут предъявлять различные требования к конструкции резонатора (особенно в отношении модовой структуры), фазовой среде, на которой вводится информация (термопластик, Эйдофор, ультразвуковая волна в жидкости, двупреломляющий кристалл, фазовая голограмма). В некоторых случаях обработки информации затруднительно обеспечить требуемые характеристики из-за значительных шумов, вносимых существующими носителями информации. Следует указать на ряд свойств систем с внутрирезонаторными объектами, интересных для распознавания образов. Свойство активного процесса формирования изображения осуществлять подчёркивание контуров /6/ может найти применение в устройствах распознавания, поскольку наиболее существенная для распознавания информация содержится в контурах изображения. На этом принципе могут быть построены нелинейные дискриминантные элементы, осуществляющие более сложные операции в системах распознавания образов, чем это позволяют линейные когерентные системы.
Принцип реактивной фильтрации интересен для распознавания объектов, которые расположены внутри импульсного ОКГ или могут вводиться внутрь без существенного уменьшения энергии генерации. К таким объектам относятся биологические фазовые объекты (если они обладают низкими потерями и достаточной устойчивостью), частицы тумана, частицы в струе, истекающей из реактивных двигателей, частицы аэрозолей, для которых необходимо определить распределение микрообъектов по размерам. На рисунке 5 приведена возможная схема анализа аэрозолей или горячих микрочастиц. Трудности, связанные с достижением быстродействия регистрирующего устройства, могут быть исключены при использовании мультиплексированного голографического фильтра,
- 426 -
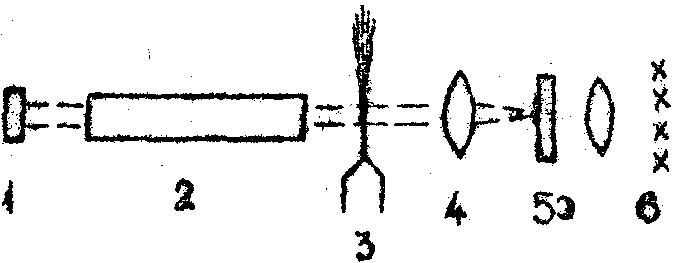
Рис.5. Схема для анализа аэрозолей:
1 - зеркало ОКГ; 2 - активное вещество; 3 - инжектор аэрозолей; 4 - линза; 5 - фильтр} 6- плоскость регистрации.
содержащего эталоны различной формы и ориентации, и матрицы быстродействующих фотодиодов.
Известно, что в твёрдотельной лазере превышение порога генерации приводит к возрастанию числа типов колебаний, причём многомодовый режим в значительной степени обусловлен неоднородностью активного вещества, пространственно неравномерной накачкой, а также ошибками юстировки резонатора, аберрациями зеркал и других оптических элементов. Некоторые неоднородности кристалла и аберрации оптических элементов могут быть исключены голографическим методом. Записав на голограмму аберрации оптических элементов и активного вещества, можно воспользоваться голограммой как компенсирующей пластинкой аналогично тому, как это делается при компенсации аберраций лине.
Реактивная реконструкция представляет интерес для голографического телевидения и кинематографа с сокращенной полосой частот. В такой системе телевидения предлагалось использовать небольшую голограмму /7/ вместе со специальным рассеивающим экраном. Поместив голограмму внутрь резонатора /5/, получим значительный выигрыш в освещённости, что весьма важно для телевизионной проекции. В качестве среды для записи гояограммы электронным лучом внутри резонатора можно использовать масляную плёнку или электроннооптический модулятор. Гипотетическая схема голографического телевидения приведена на рис. 6.
- 427 -
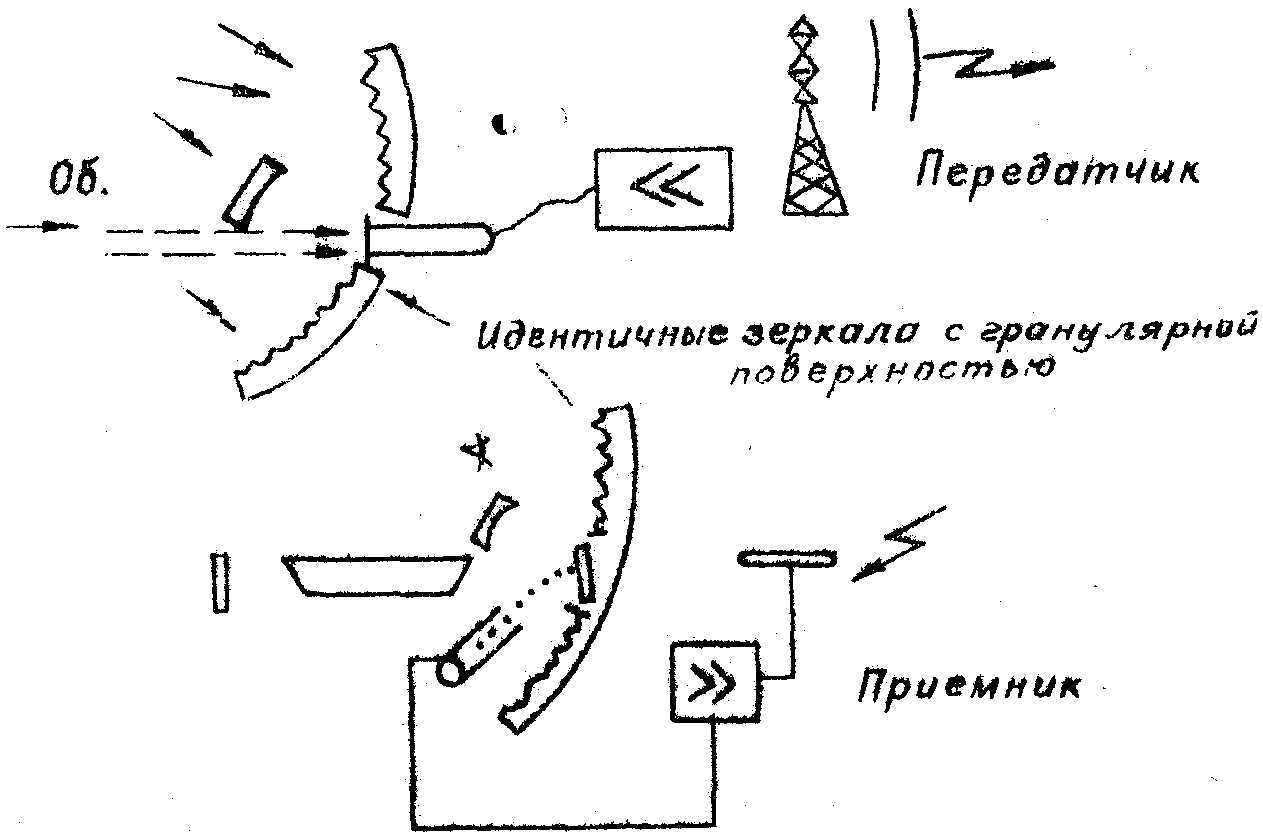
Рис.6. Гипотетическая телевизионная система.
- 428 -
Л и т е р а т у р а
1. R.V.Pole, H.Wieder, R.A.Myers. Appl.Phys.Letters, 8, 9, 229-231 (1966).
2. R.V.Pole, H.Wieder, E.S.Barrekette.
I - Appl.Optics, 6, 9, 1571 (1967).
II - Appl.Opt1cs, 6, 10, 1761 (1967).
3. Г.А.Соболев. Авторское свидет. №224714 с приоритетом от 6/IX-1965 г. Бюллетень изобретений № 26, 1968.
4. Л.Д.Бахрах, О.Н.Владимирова, А.П.Курочкин, Г.А.Соболев, Г.Х.Фридман. Применение методов когерентной оптики и голографии к задачам антенной техники и обработке информации. Сб. Антенны, №2, изд. "Связь", М., 1967.
5. Г.А.Соболев, Е.Р.Цветов. Техника кино и телевидения, №2, стр.28-37 (1968).
6. В.Харди. Активное формирование изображения в лазерах. Сборник, "Оптическая обработка информации", М., изд. "Мир", 1966.
7. K.A.Haines, D.B.Brumm. Proc. IEEE, 55, 8, 1512 (1967).
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

