КОГЕРЕНТНОСТЬ
В ФИЗИКЕ
Я.Смородинский
Я
не знаю, кто и когда первый ввёл в физику понятие о когерентности;
во всяком случав, в прошлом веке это уже было хорошо известно.
Оптики называли когерентными такие источники света, которые
способны интерферировать друг с другом. Кроме оптиков когерентностью
почти никто не интересовался.
однако
с открытием квантовых свойств света и волновых свойств частиц
положение изменилось. Суперпозиция состояний, резонанс в химических
реакциях, распады мезонов и много других явлений оказались
связанными с когерентностью.
Когерентность
была очень интересно и эффективно использована в ранних работах
Эйнштейна. К 1909 году Эйнштейн уже знал. термодинамику, которую
он открыл, не зная о работах Гиббса, теорию броуновского движения
и теорию флуктуаций. Кроме того, он уже знал специальную теорию
относительности, из которой следовало, что свет обладал энергией,
обладает и импульсом, и, наконец, он знал знаменитую формулу
Планка.
Всё
это вместе, счастливо сочетавшееся в руках одного человека,
привело Эйнштейна к размышлению о том, как флуктуирует плотность
излучения, находящегося в термодинамическом равновесии в некоторой
полости. Термодинамика даёт следующую формулу для средней
квадратичной флуктуации плотности излучения:
d
2=(Е- )2=-
)2=-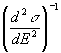 =-
=-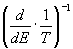
(Е,
s - спектральные плотности энергии и энтропии из 1 си3).
Из этой формулы можно вычислить флуктуации, излучения, если
известна формула для плотности энергии. Для этого надо воспользоваться
формулой Планка
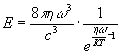
и
выразить 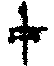 через спектральную плотность энергии Е. Дифференцируя еще
раз по Е, получим
через спектральную плотность энергии Е. Дифференцируя еще
раз по Е, получим
d
2=ћw Е+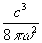 Е2
Е2
Тот
факт, что формула для флуктуации составлена из двух слагаемых,
имеет замечательное следствие.
Первый
член выглядит так, как будто бы свет состоял из отдельных
частиц (мы теперь знаем - квантов), которые влетают и вылетают
из объёма совсем независимо друг от друга. Если обозначить
число квантов в единице объёма через n, а флуктуацию в числе
квантов через D n=d /ћw , то первый член можно
записать так:

Такая
формула для флуктуации получается, например, в ансамблях,
описываемых распределением Пуассона:
Р(n)=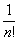 xne-x
xne-x
где
х - среднее значение n. Таким образом, первый член указывает
на статистическую независимость - полную некогерентность квантов.
Напротив второй член описывает флуктуации полностью когерентного
классического волнового поля. Такая формула флуктуаций излучения
получается, если излучение описывается классической формулой
Релея-Джинса:
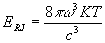
Отсюда
сразу получается:
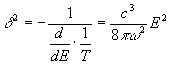
Формула
для флуктуации показывает очень наглядно дуальную (корпускулярно-волновую)
природу поля излучения. Можно сказать, что в эффекте флуктуации
оба аспекта разделились и пoлe излучения предстаёт как смесь
когерентной - волновой части и некогерентной - квантовой.
При этом квантовая часть преобладает при больших частотах
(ћw >KT), а волновая - при малых (ћw <<KT).В
действительности в этой картине заложены уже основы и статистической
интерпретации квантовой механики, поскольку в ней некогерентность
и квантовость оказываются разными сторонами одного и того
же явления.
Аналогичную
формулу можно получить и для давления излучения (поскольку
давление 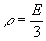 ).
Давление, например, на подвешенное зеркальце также флуктуирует.
Флуктуации давления также состоят из двух частей: когерентного
действия поля излучения, при котором разные волны интерферируют,
давая вклад, пропорциональный квадрату числа квантов, и некогерентного
действия отдельных квантов, приводящего к линейному члену.
).
Давление, например, на подвешенное зеркальце также флуктуирует.
Флуктуации давления также состоят из двух частей: когерентного
действия поля излучения, при котором разные волны интерферируют,
давая вклад, пропорциональный квадрату числа квантов, и некогерентного
действия отдельных квантов, приводящего к линейному члену.
Разделение
равновесного излучения, находящегося в тепловом равновесии,
на когерентную и некогерентную части должно были найти своё
отражение и в процессах излучения света. Для того, чтобы излучение
могло находиться в равновесии со стенками или же с любыми
объектами внутри полости (их любили называть осцилляторами),
необходимо, чтобы вероятность излучения и поглощения света
такими осцилляторами была бы связана определёнными соотношениями.
Соотношения эти не должны зависеть от конкретных свойств осцилляторов
- требование обычное в термодинамических рассуждениях. Так
возникла идея о коэффициентах излучения Эйнштейна (1919).
Простые рассуждения привели к заключению, что вероятность
поглощения света должна быть пропорциональна числу квантов
(заданной частоты и поляризации), находящихся в поле излучения
Nu (т.е. плотности энергии излучения), а вероятность
излучения света должка быть пропорциональна Nu +1. Такую
зависимость легко понять, если заметить, что: 1) кванты одной
и той же частоты и поляризации не различимы и 2) для равновесия
надо, чтобы вероятность поглощения, после того как
квант излучен, была бы равна вероятности его излучения, тогда
он поглотится с той же вероятностью, что и излучится, и число
квантов в среднем изменяться не будет.
Итак,
вероятности излучения и поглощения относятся как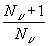 .
.
Вероятность
излучения можно, таким образом, разбить на две части: спонтанное
излучение, вероятность которого не зависит от Nu , и
вынужденное (индуцированное) излучение с вероятностью, пропорциональной
Nu . Вынужденное излучение когерентно, на его свойствах
основан принцип действия мазеров и лазеров.
Спонтанное
излучение некогерентно. Источник подчиняется просто закону
радиоактивного распада (экспоненциальному закону). Радиоактивный
распад обладает важный свойством. По самому своему определений
он является процессом, при котором система полностью "забывает"
свою историю. Так как при изменении начала отсчёта времени
t→t+ экспоненциальная функция остаётся экспоненциальной, то система
не сохраняет информации о моменте своего рождения. Она, очевидно,
не сохраняет никакой информации и о деталях своего устройства
(кроме как об энергии системы - в силу закона сохранения).
Таким свойством может, строго говоря, обладать только квантовая
система - возбуждённый атом, радиоактивное ядро. Классическая
механическая (замкнутая) система обратима во времени, и по
её поведению в принципе можно восстановить её историю (механическая
система "помнит" своё прошлое).
экспоненциальная функция остаётся экспоненциальной, то система
не сохраняет информации о моменте своего рождения. Она, очевидно,
не сохраняет никакой информации и о деталях своего устройства
(кроме как об энергии системы - в силу закона сохранения).
Таким свойством может, строго говоря, обладать только квантовая
система - возбуждённый атом, радиоактивное ядро. Классическая
механическая (замкнутая) система обратима во времени, и по
её поведению в принципе можно восстановить её историю (механическая
система "помнит" своё прошлое).
Спонтанное
излучение связно поэтому с принципиальной "забывчивостью"
распадающейся системы, что и приводит к его полной некогорентности.
Таким
образом, система, излучающая спонтанно, представляет собой
эталон абсолютно некогерентного источника.
Мы
видим, что флуктуационные свойства света оказались связанными
с законами его излучение и поглощения.
Для
построения замкнутой теории света не хватало ещё одного шага:
надо было вывести формулу Планка из общих соображений статистической
физики (следуя Больцману) без привлечения посторонних аргументов,
вроде формулы Вина или формулы для числа колебаний поля, которые
использовались при старых способах вывода формулы теории излучения.
Этот
пробел был заполнен в 1924 году пакистанским физиком Бозе.
Вывод Бозе (он практически в неизменном виде излагается во
всех учебниках) использует два факта: 1) свет состоит из квантов
и 2) кванты не различимы. Второе свойство содержит в себе
волновую гипотезу, так как фактически "обобществляет" степени
свободы.
Вывод
Бозе был сразу же (в 1925 г.) распространён Эйнштейном на
одноатомный газ. Одноатомный газ отличается от газа квантов
только другой связью между энергией и импульсом. Фотонный
газ - предельно релятивистская система, одноатомный газ -
система нерелятивистская. Поэтому не удивительно, что для
одноатомного газа была получена флуктуационная формула, похожая
на формулу для квантов. Для газа атомов нагляднее говорить
не о флуктуации энергии, а о флуктуациях числа частиц D
n. Для этой величины получается формула*
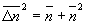
Первый
член, как мы уже знаем, вполне понятен: это обычная пуассоновская
флуктуация независимых событий; второй член был неожидан,
ибо он, как мы тоже знаем, описывает когерентные флуктуации,
понятные для света, но непонятные в то же время для атомов.
Квадратичные флуктуации отражали волновые свойства атомов
(введённые, как отмечалось, гипотезой об их неразличимости).
Это было первое
*
В формуле для флуктуации излучения плотность энергии относится
к единице объема и единичному интервалу частоты; последнее
даёт лишнй множитель с3/8p w 2
проявление
волновых свойств материи, открытое теоретически. Эйнштейн
не прошёл мимо него и отметил, что атомы должны давать интерференционную
картину.
Спустя
несколько лет была получена ещё одна флуктуационная формула
для систем, подчиняющихся принципу Паули. Оказалось, что в
таких системах некогерентные и когерентные флуктуации не складываются,
а вычитаются (минус перед квадратичным членом*).
Открытие
волновых (когерентных) свойств вещества развилось в новую
науку - квантовую механику. С точки зрения квантовой механики
становятся понятными многие свойства, которые были необъяснимы
со старых некогерентных позиций. Для нас сейчас особенно поучительна
та форма квантовой механики, которую ей придал Фейнман. В
этой форме оказывается более наглядной связь между корпускулярной
и волновой картинами.
Амплитуда
вероятности, переходя из точки А в точку В, в этой картине
описывается как когерентная смесь амплитуд, отвечающих всем
возможным (виртуальным) путям, которые можно провести из точки
А в точку В.
Вклад
каждой "парциальной" амплитуды определяется функцией действия,
вычисленной вдоль определённого пути по формулам классической
механики
S=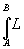 dt
dt
(L-
функция Лагранжа). Формула для вклада каждого из путей имеет
вид:
D
y
=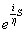
Операция
интегрирования по путям может быть определена строго, и в
математике есть методы вычисления таких интегралов.
В
такой картине классическая траектория возникает как результат
интерференции многих (бесконечно многих) траекторий. Здесь
к
Знак когерентных флуктуаций определён однозначно, так как
при малых плотностях система должна переходить в Пуассоновскую.
становится
понятнее природа принципа наименьшего действия. Классическая
частица не может "осмотреть" все виртуальные траектории и
выбрать из них ту, которая отвечает наименьшему действию.
При описании в форме "интеграла по путям" такой "осмотр" естественным
образом содержится в самом механизме образования амплитуды.
Можно отметить еще одно любопытное свойство волновой картины.
При описании движения частиц в классической механике можно
формально считать, что частицы движутся в трёхмерном многообразии,
погруженном в пространство любой размерности. Например, можно
считать, что они движутся в трёхмерной гиперплоскости четырёхмерного
(евклидова) мира. В этом смысле трёхмерность пространства
выглядит условием внешним по отношению к механике (которая
говорит лишь о трёхмерности движения). Для волновых движений
это не так: волна в трёхмерном мире не сводится просто к трёхмерной
волне в мире 4-х измерений так же, как поле от заряда на плоскости
не описывается, двухмерным потенциалом. Можно поэтому сказать,
что вволновых явлениях трёхмерность пространства подвергается
экспериментальной проверке (например, по характеру интегрирования
по траекториям). Понятие когерентности не ограничивается лишь
соотношениями между значениями полей в двух разных пространственно-временных
точках (корреляциями). В оптике и квантовой механике очень
часто говорят о когерентности двух состояний. Так, излучённый
свет обладает определённой поляризацией. Если, например, свет
поляризован линейно, то можно с таким же успехом говорить,
что он представляет собой когерентную смесь правополяризованного
состояния и левополяризованного состояния. Хорошо известно,
как обращаться с такими состояниями. Важно то, что существует
всегда набор ортогональных (т.е. неинтерферирующих) состояний,
по которым можно разложить любое когерентное состояние. Одним
из самых эффектных примеров демонстрации когерентных свойств
квантовомеханической системы служит распад нейтрального каона
(К°-мезона). Каоны - частицы в 980 раз тяжелее электрона.
Они бывают заряженные и нейтральные. Каоны К+ и
К0 образуют дуплет - они рождаются, например, в
реакциях:
N
+ p +
→ L 0
+ K+
N
+ p 0
→ L 0
+ K0
(N
- нейтрон, L 0 - гиперон). У них, как и у других
частиц, есть античастицы К- и анти К0,
который обозначается как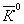 .
Эти частицы распадаются при столкновениях с антинуклонами:
.
Эти частицы распадаются при столкновениях с антинуклонами:
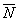 + p -
→
+ p -
→ 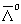 + K-,
+ K-,
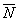 + p 0
→
+ p 0
→ 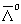 + K0.
+ K0.
К-
и К+, конечно, легко отличить друг от друга - у
них разные заряды, а заряды сохраняются; поэтому К-
сам по себе не может превратиться в К+. Если в
какой-либо реакции рождается пара К+ и К-,
то легко их идентифицировать и сказать, какой из них К+,
а какой К-.
Совсем
иначе обстоит дело с К0 и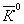 .
Здесь положение скорее похоже на положение с поляризациями
света. Если рождается пара К0 и
.
Здесь положение скорее похоже на положение с поляризациями
света. Если рождается пара К0 и 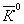 ,
то они представляют собой когерентную смесь обеих частиц,
и мы можем говорить о смеси К0 +
,
то они представляют собой когерентную смесь обеих частиц,
и мы можем говорить о смеси К0 +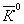 так
же, как о смеси двух поляризаций света. Нейтральные каоны
живут недолго. Они распадаются со временем 0,8× 10-10сек.
на два пиона или со временем 5× 10-8 сек.
на три пиона. Эти слова надо уточнить. Частица, родившаяся
в какой-либо реакции, не может распадаться с двумя разными
временами. Более аккуратное рассмотрение (подтвержденное и
опытом) показывает, что родившийся К0 мезон можно
рассматривать как когерентную смесь двух каонов КS0
и КL0 (короткоживущего и долгоживущего).
КS0 распадается по схеме КS0
→ p +p со
временем 0,8× 10-10сек., КL0
распадается по схеме KL0 → p
+p +p со временем 5× 10-8сек. Распады
КL0→3p
и КS0→2p
долгое время считались запрещёнными законом сохранения комбинированной
или временной чётности. Мы не будем здесь более подробно говорить
об этом законе; о нём можно сейчас прочесть в любой книге
по элементарным частицам.
так
же, как о смеси двух поляризаций света. Нейтральные каоны
живут недолго. Они распадаются со временем 0,8× 10-10сек.
на два пиона или со временем 5× 10-8 сек.
на три пиона. Эти слова надо уточнить. Частица, родившаяся
в какой-либо реакции, не может распадаться с двумя разными
временами. Более аккуратное рассмотрение (подтвержденное и
опытом) показывает, что родившийся К0 мезон можно
рассматривать как когерентную смесь двух каонов КS0
и КL0 (короткоживущего и долгоживущего).
КS0 распадается по схеме КS0
→ p +p со
временем 0,8× 10-10сек., КL0
распадается по схеме KL0 → p
+p +p со временем 5× 10-8сек. Распады
КL0→3p
и КS0→2p
долгое время считались запрещёнными законом сохранения комбинированной
или временной чётности. Мы не будем здесь более подробно говорить
об этом законе; о нём можно сейчас прочесть в любой книге
по элементарным частицам.
Соотношения
КS0 и КL0 вместе
составляют К0. Можно, однако, сказать и иначе:
можно сказать, что КS0 представляет
собой когерентную смесь К0 и анти К0.
Когда пучок КL0 попадает в мишень, то
анти К0 аннигилируют с нуклонами мишени и из мишени
выходит чистый пучок К0. Через 10-10
сек. КS0 распадаются, и мы опять остаёмся
с пучком КL0.
Мы
видим, что бывают случаи, когда трудно сказать, что мы должны
считать частицей. Если считать по рождению, то частицами надо
называть К0 и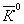 :
они появляются в разных реакциях самостоятельно. Если же следить
за поведением в вакууме, то естественно называть частицей
то, что распадается по экспоненциальному закону, так как две
разные экспоненты никак не связаны друг с другом, если нет
между ними интерференции.
:
они появляются в разных реакциях самостоятельно. Если же следить
за поведением в вакууме, то естественно называть частицей
то, что распадается по экспоненциальному закону, так как две
разные экспоненты никак не связаны друг с другом, если нет
между ними интерференции.
Состояния
КS0 и КL0 действительно
почти не интерферируют (совсем недавно считали, что они совсем
не интерферируют). Однако оказалось, что интерференция всё
же есть; около 0,3% КL0 кончают своё
существование распадом на 2p , совсем как КS0.
Таким образом, способ распада перестал быть однозначной приметой
частицы. Характеристикой частицы остались её масса и время
жизни. КL0 оказалась немного тяжелее
КS0, поэтому их всё же можно считать
разными частицами. Но распадаясь одинаковым образом на два
пиона, частицы КS0 и КL0
коррелируют во времени. Это значит, что существует временная
интерференция их распадов. Пучок частиц, в котором есть как
КS, так и КL (это значит, что мы ведём
наблюдения вблизи ускорителя), распадается не по формуле,
представляющей собой сумму двух экспонент:
N0Se-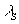 t
+ N0Le-
t
+ N0Le-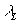 t
t
(N0S,
N0L - начальное количество КS0
и КL0; l S и l
L их постоянная распада.
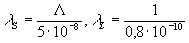 )
)
Такой
закон распада получался бы, если бы оба типа мезонов распадались
независимо. Но так как они интерферируют, то возникает ещё
один член, периодически меняющийся во времени.
N0Se-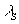 t
+2
t
+2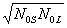 ×
Cos
×
Cos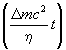 + N0Le-
+ N0Le-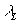 t
t
В
этой формуле D m есть разность масс КS0
и КL0. Такой закон распада действительно
наблюдался, из него даже определили разность масс обеих частиц.
Такое явление есть не что иное, как хорошо известное из теории
колебаний биение.
Разность
масс оказалась очень малой:
m(КL0)
– m(КS0) @ 10-3 эв »
0,5× 10-11 массы электрона.
Самая
маленькая разность масс частиц, которую измерили физики, в10-14
раз меньше массы- самих К0.
Возможность
интерференции двух состояний нейтрального каона связана с
нарушением закона сохранения, который долгое время считался
незыблемым, - закона сохранения временной чётности. Симметрия
во времени процессов квантовой механики требовала, чтобы сдвиг
фаз между рождающимися КS0 и КL0
был бы равен 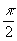 .
Наличие интерференции показывает, что реальный сдвиг фаз отличается
от
.
Наличие интерференции показывает, что реальный сдвиг фаз отличается
от 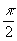 , так
что состояния КS0 и КL0
оказываются не вполне ортогональными друг другу. Напомним,
что само появление двух нейтральных каонов было связано с
нарушением закона сохранения частиц, благодаря которому возможно
было перемешивание (и интерференция) частицы К0
и античастицы
, так
что состояния КS0 и КL0
оказываются не вполне ортогональными друг другу. Напомним,
что само появление двух нейтральных каонов было связано с
нарушением закона сохранения частиц, благодаря которому возможно
было перемешивание (и интерференция) частицы К0
и античастицы 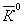 .
Если бы зарядовая чётность сохранялась, то эти состояния были
бы ортогональны друг другу. Тогда масса К0 и равная
ей масса
.
Если бы зарядовая чётность сохранялась, то эти состояния были
бы ортогональны друг другу. Тогда масса К0 и равная
ей масса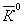 были
бы строго заданы, и ничего парадоксального в физике квантов
мы бы не нашли.
были
бы строго заданы, и ничего парадоксального в физике квантов
мы бы не нашли.
Ещё
с одним аспектом когерентности мы встречаемся в задаче многих
чисел - теории твёрдого числа и теории ядра.
Движение
отдельных частиц, вообще говоря, происходит независимо. Но
если частицы сильно взаимодействуют друг с другом, то их движения
оказываются коррелированными и возникает то, что называется
коллективными движениями. В ядре коллективные степени свободы
приводят к колебательным и вращательным уровням ядра. Ими
обусловлено в основном явление деления. По существу дела и
здесь идет речь о когерентности состоянии разных частиц, обусловленной
тем, что частицы, подобно фотонам, не различимы друг от друга.
Когерентность движений разных частей системы позволяет даже
изменить точку зрения на теорию систем, состоящих из многих
частиц. Сейчас обычно когерентное движение системы рассматривается
как основное, а частицы выступают как элементарные возбуждения
системы. В этой картине возбуждения называют квазичастицами;
их впервые (под названием экситонов) рассмотрел Френкель.
Порой, как это происходит в ядре, масса квазичастиц совпадает
с массой свободных частиц (нуклоны в ядре) и различие между
частицами и квазичастицами становится несущественным. В других
случаях (электроны в висмуте, например) это различие вполне
ощутимо. Когерентные движения в квантовых системах имеют порой
весьма парадоксальные свойства. Достаточно привести в качестве
примеров сверхпроводящий ток (который даже описывается подобием
волновой функции как настоящее когерентное состояние) и сверхтекучее
движение гелия, связанное о когерентными свойствами основного
состояния Бозе-газа (так называемая Бозе-конденсация).
Рассмотрение
свойств задачи многих тел выходит за рамки этой лекции.

