- 295 -
ОСНОВЫ ГОЛОГРАФИЧЕСКОЙ ТЕХНОЛОГИИ
И.П.Налимов
1. Голографические изображения высокого разрешения, используемые в технологических процессах микроэлектроники
В настоящее время в технологических процессах микроэлектроники большую роль играют проекционные методы изготовления фотошаблонов и нанесения изображений микросхем на фоторезист. В современных процессах требуется обеспечить разрешение изображения порядка 0,5 мкм по максимальному полю. Для этого нужны линзовые системы высокой апертуры с задним углом раскрытия 900 и выше. При любых усилиях обеспечить большое поле таких линз оптики неизбежно наталкиваются на аберрации. Принципиальное устранение аберраций линз невозможно, хотя специальная оптическая технология способна уменьшить эти ошибки, применяя сложные системы линз - объективы.
Оптикам-вычислителям известны методы уменьшения отдельных аберраций, но все же каждый конкретный случай требует длительных расчётов и использования различных сортов стекла. Хотя в этом отношении технология расчёта и изготовления линз приближается к пределу, ей не удаётся обеспечить микронное разрешение по полю свыше нескольких сантиметров.
В связи с этим в данной лекции предпринимается попытка определить возможности применения голограмм для проектирования изображений высокого разрешения на большой площади.
Случай голограмм малой апертуры x/z<<1, где х - размер голограммы, z - расстояние предмет - голограмма, поддается простому теоретическому описанию и был подробно рассмотрен в работах /1,2/. В этом случае размер наименьшей детали восстановленного изображения превышает 10l
. Следовательно, для целей фотолитографии этот случай интереса не представляет. В более общем плане, поскольку
- 296 -
изготовить безаберрационную линзу с малой апертурой нетрудно, то в этом случае голограмма не имеет преимущества перед линзой в смысле разрешения в изображении и размеров поля изображения.
Для технологических процессов микроэлектроники необходимо использовать голограммы с апертурой x/z>1 и даже x/z>>1. Уникальная особенность голографии состоит в том, что она в такой геометрии (приближающейся к квазиконтактной) позволяет в принципе получать идеальные действительные изображения любых размеров и с разрешением, ограниченным только дифракционным пределом. Для получения идеального изображения здесь надо, казалось бы, немного: в точности повторить геометрию записи при восстановлении. Если нас интересует действительное изображение, то восстанавливающий пучок должен идти в направлении, обратном опорному пучку при записи, но кривизна обоих пучков в плоскости эмульсии голограммы должна в точности совпадать. При этом аберрации в их линзовом понимании отсутствуют вовсе, и разрешение в восстановленном изображении ограничено лишь дифракционным пределом и приближается к 2/l
в квазиконтактном случае.
При этом, конечно, предполагается, что экспериментальная техника обеспечивает выполнение остальных условий:
1) подложка голограммы однородная и микроплоская, благодаря чему обращение пучка не изменит условий освещения каждой точки эмульсии;
2) режим экспозиции и обработки эмульсии выбран правильно; это должно обеспечить достаточный контраст изображению;
3) эмульсия голограммы имеет разрешение, обеспечивающее равномерную запись всех пространственных частот при данном максимальном угле между опорным и объектным пучками.
В настоящей работе нас будет интересовать лишь влияние несохранения геометрии записи при восстановлении на качество восстановленного изображения. Причиной несохранения могут являться неточности установки голограммы в заданную позицию, механические смещения эмульсии в результате натяжений в желатине /3/, доворот восстанавливающего пучка, вызванный усадкой эмульсии при проявлении и т.д.
- 297 -
Принципиальное отличие геометрической оптики голограмм с малой и большой апертурой состоит в том, что в первом случае определяют положение и форму изображения, мало интересуясь его разрешением, а во втором случае положение и форма строго заданы - это положение и форма начального объекта. Надо определить либо качество изображения при заданной геометрии и условиях опыта, либо, наоборот, определить оптимальную схему и допуски на сохранение геометрии, исходя из заданных размеров и разрешения изображения.
Здесь речь будет идти о голографических изображениях с коэффициентом увеличения, равным единице, хотя мыслимы методы получения идеальных изображений с увеличением или уменьшением. Очевидным методом достижения этого является одновременное и пропорциональное изменение масштаба голограммы и длины волны восстанавливающего пучка. Однако пока не ясно, как практически реализовать уменьшение голограммы - микронной структуры большой площади.
2. Сравнение голографических и линзовых систем
На основе лучевых представлений можно развить геометрическую оптику восстановленного голографического изображения. Для исследования этого вопроса полезно использовать аналогию с линзовой оптикой, где геометрическая теория качества, оптического изображения разработана подробно.
Однако эту аналогию можно использовать лишь в ограниченной мере, поскольку существует ряд принципиальных отличий голографических систем от линзовых. Расчёт линзовых систем строится на трёх основных свойствах этих систем:
1) аксиальная симметрия,
2) параксиальность изображения, связанная с тем, что предмет всегда располагается на расстоянии от линзы, большем ¦
, которое, в свою очередь, всегда больше h (радиуса линзы). Другими словами, всегда светосила изображающих систем h/f<1
- 298 -
3) все лучи, образующие точку изображения, проходят одинаковый путь от точки до объекта.
Как нетрудно видеть, в негауссовом случае (x/z>1) голографическая система не обладает ни одним из этих свойств. Аксиальная симметрия отсутствует. Предмет может располагаться вплоть до контактного положения с голограммой. Длина лучей от восстанавливающего источника С до точки изображения 0' - переменная величина, зависящая от выбора точки на голограмме.
Однако внимательный анализ негауссовых голографических систем обнаруживает ряд их особенностей, которые в какой-то степени можно сопоставить со свойствами линзовых систем, и на их основе провести расчёт положения голографического изображения.
Третий критерий Максвелла неприменим в голографии
Согласно критериям Максвелла оптическая система может считаться идеальной, если она:
1) даёт точечное изображение каждой точки предмета, т.е. сохраняет гомоцентричность пучков,
2) обладает постоянным увеличением для двух любых точек изображения (изображение подобно предмету);
3) переводит нормальную оси плоскость в пространстве предмета в нормальную оси плоскость в пространство изображения.
Как известно, ни одна линзовая система не удовлетворяет критериям Максвелла в полной мере. Можно говорить лишь о приближении к идеальному изображению в параксиальной области. Усилия вычислительной оптики направлены на увеличение этой области и удержание отклонений от идеальности изображения в допустимых пределах за счёт специальной конфигурации стеклянных поверхностей и их комбинирования.
В голографии третий критерий в таком виде неприменим, поскольку обычно (кроме схемы Габора) осевая симметрия отсутствует, хотя можно выделить оптическую ось (так называемую нулевую линию), обладающую особыми свойствами. Применительно к голографии третий
- 299 -
критерий должен требовать перехода плоскостей предмета, параллельных гол огранке, в плоскости изображения, также параллельные голограмме. Очевидно, только в одном частном случае - сохранении геометрии записи при восстановлении - все критерии Максвелла удовлетворены: точка изображения соответствует точке предмета с точностью до дифракции, увеличение равно единице и параллельность плоскости сохраняется. Во всех остальных случаях можно требовать лишь приближённого выполнения критериев для определённого участка пространства изображений. Задачей геометрической оптики негауссовых голограмм должно быть определение геометрических параметров схемы по заданным размерам и качеству изображения. Необходимость в создании вычислительной голографической оптики в негауссовом случае обусловлена тем, что реальная голограмма не может в точности повторять "эфирную", т.е. ту стоячую интерференционную картину электромагнитного поля, которая создаётся в объёме при наложении предметного и опорного пучков. Поэтому сохранение условий записи при восстановлении всегда приближённое.
Качество изображения, создаваемого голограммой, в реальных условиях определяется следующими факторами.
1. Регистрирующая среда. Например, изменение рисунка в результате проявления фотоэмульсии ведёт к отличию реальной голограммы от "эфирной". Понятно, что "эфирная" голограмма никакими способами не может быть наблюдаема в чистом виде. Но необходимо, чтобы голограмма, зарегистрированная в среде, минимально отличалась от "эфирной". Для практических целей зачастую достаточно обеспечить линейность отклика фотослоя на интенсивность светового интерференционного поля.
2. Помехи, например, повреждения эмульсии, приводят к тому, что голограмма работает не всей поверхностью и контраст изображения снижается. Если для каждой точки предмета записывать несколько голограмм, например путём рассеянного или многостороннего освещения предмета, то влияние помех можно уменьшить.
3. Геометрия. Необходимо, чтобы голограмма работала при строго заданной расположении источников, определяемом как сохранение
- 300 -
геометрии записи при восстановлении изображения.
В обычных оптических системах трудности заключаются в расчёте нужного распределения показателя преломления стекла и последующей обработке стекла.
Трудности реализации идеальных оптических систем в географии переносятся со стекла на качество регистрирующих сред и коллимирующей осветительной оптики.
Центр тяжести проблемы создания коротких голографических систем, образующих изображения большого формата и разрешения с дифракционный пределом переносится на разработку регистрирующих сред с достаточно линейным откликом, изучение влияния отклика среды на качество восстановленного голографического изображения, а также на проблему сохранения геометрии записи при восстановлении.
Голограмма не строит изображения. (в линзовом понимании)
Как известно, две сферические поверхности линзы обеспечивают
преобразование всех точек предметного пространства в соответствующие точки пространства
изображения. Необходимость изображающей системы работать на много точек изображения,
а не на одну, сильно ограничивает её возможности. Так, светосила линзовой системы
2h/¦
не может быть больше 2, где
2h - диаметр входного зрачка, ¦
-
фокусное расстояние системы. Практически это ограничивает размеры поля изображения,
если требуется высокое разрешение. Если требуется повысить разрешение на оси,
то надо уменьшать ¦
. Однако величина
2h накладывает предел этому уменьшению.
При приближении ¦
к
2h края линзы перестают давать изображение
для крайних точек поля. Для увеличения разрешения по полю линзовых систем необходимо
уменьшать фокусное расстояние системы. Например, при единичном увеличении расстояние
от изображения до главной плоскости линзы
r'=2¦ . Это
означает, что наименьший разрешённый элемент изображения на оси имеет размеры
не менее 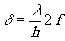 .
Таким образом, имеется два противоречивых требования:
1) ¦ →О
и 2) h/¦
=1, которым нельзя удовлетворить одновременно.
Это противоречие
.
Таким образом, имеется два противоречивых требования:
1) ¦ →О
и 2) h/¦
=1, которым нельзя удовлетворить одновременно.
Это противоречие
- 301 -
не позволяет в проекционной оптике создавать изображение с разрешением, ограниченным лишь волновой природой света, на значительных площадях. В настоящее время не известны линзовые системы, давшие разрешение 1 мкм на площади более 40х40 мм2.
В неизображающих системах, таких как параболические зеркала прожекторов и гелиоустановок, возможно за счёт выбора больших зеркал (h>>¦
) получение светосилы 3:1, 5:1 и даже больше. Такие системы обладают значительной комой (она тем выше, чем больше светосила) и не годятся для съёмки предметов, имеющих сколько-нибудь отличные от нуля угловые размеры.
В голографии неизображающие системы такого типа становятся изображающими. Ограничение по светосиле, характерное для проекционных линзовых систем, снимается. Это в принципе делает возможной проекцию предметов любых размеров, причём разрешение в каждой точке изображения ограничено лишь дифракционным пределом. Каждой точке изображения на голограмме соответствует интерференционный рисунок типа участка зонной пластинки Френеля, который можно физически выделить (осветив, например, при голографировании только эту точку). Его можно назвать "парциальной голограммой" данной точки изображения, поскольку она ответственна за формирование изображения только в этой точки. Таким образом, каждая "парциальная голограмма" работает не на участок изображения, как в проекционной линзовой оптике, а лишь на одну точку, как в гелиоустановке. Ввиду использования сферических волновых фронтов в голографии наряду с комой существенную роль будут играть сферические аберрации. Отсутствие осевой симметрии в голографии приводит к несимметричным аберрациям, которые в линзовой оптике устраняются путём центровки системы. Поскольку далее мы будем рассматривать только голограмму точки, то термин "парциальная" будем для краткости опускать.
- 302 -
В голографии неприменим принцип Ферма в том виде, в каком он используется в геометрической оптике
В обычной геометрической трактовке принцип Ферма гласит, что из всех возможных трасс в преломляющей среде луч выбирает ту, на которую затрачивается минимальное время. Из принципа Ферма вытекает закон Снелла для преломляющей поверхности
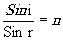
где i и r- углы с нормалью к поверхности до и после преломления, n - показатель преломления второй среды (первая среда - воздух). Степень приближения к выполнению принципа Ферма для всех лучей, строящих точку изображения, определяет качество изображения, получаемого в линзовой системе.
В отличие от линзовых систем голограмма отроит изображение в первом дифракционном порядке и строит изображение не сразу, а в два этапа путём записи и восстановления. Уже это делает неприменимой здесь обычную трактовку принципе Ферма. Известно, что точное сохранение геометрии записи при восстановлении даёт изображение с разрешением, ограниченным дифракционным пределом. Отклонение от этой геометрии разрушает изображение. Отсюда можно сделать вывод, что в голографии действует принцип сохранения разности трасс записывающих и восстанавливающих лучей. Чем меньше эта разность, тем лучше выполняется принцип Ферма (для точек изображения) и тем выше качество изображения.
Математически возможность создания идеальных систем в голографии объясняется тем, что открывается возможность одновременного удовлетворения теоремы Ферма и формулы синусов за счёт удаления фокусного расстояния голограммы на бесконечность (т.е. сохранения геометрии записи при восстановлении).
Для математического описания действия "парциальных голограмм" в настоящей работе использована специальная система координат с началом в "центре голограммы" - в так называемой нулевой точке, лежащей на пересечений прямой, проходящей через источник освещения и данную точку предмета. Эта точка выделена среди остальных
- 303 -
точек голограммы тем, что в ней угол между опорным и объектным кучами равен нулю или p
. Далее, на основе принципа постоянства дифрагирующей силы (термин предложен в работе /4/) в каждой точке голограммы проведён расчёт возможных искажений изображения точки, обусловленный несохранением геометрии записи при восстановлении.
В дальнейшем мы будем предполагать, что опорная и восстанавливающая волны чисто сферические так же, как и объектная волна. Иными словами, все источники имеют точечные размеры.
3. Частота интерференционных полос и дифрагирующая сила
Как будет показано ниже, получение идеального изображения возможно при x/z>1 только в том случае, если дифрагирующая сила при записи в каждой точке голограммы сохраняется при восстановлении. Поясним, чем дифрагирующая сила отличается от частоты интерференционных полос.
При записи опорный источник и объект могут располагаться либо по одну сторону регистрирующей среды (рис.1), либо по разные (рис.2). Интерференционные плоскости в точках А, В, Е, F среды образуются по биссектрисам угла между объектным и опорным лучами в каждой точке голограммы. Проследим, как изменяется частота интерференционных полос по нормали к биссектрисам от точки к точке В, Е и F. Здесь и далее считаем углы положительными, если они отсчитываются от нормали к поверхности голограммы против часовой стрелки. Считаем показатель преломления среды n=1.
Пусть в некоторой точке голограммы встречаются два волновых фронта, нормали к которым образуют углы a
0 и a
r с нормалью к поверхности голограммы. Частота полос поперёк биссектрисы:
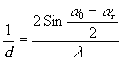
- 304 -
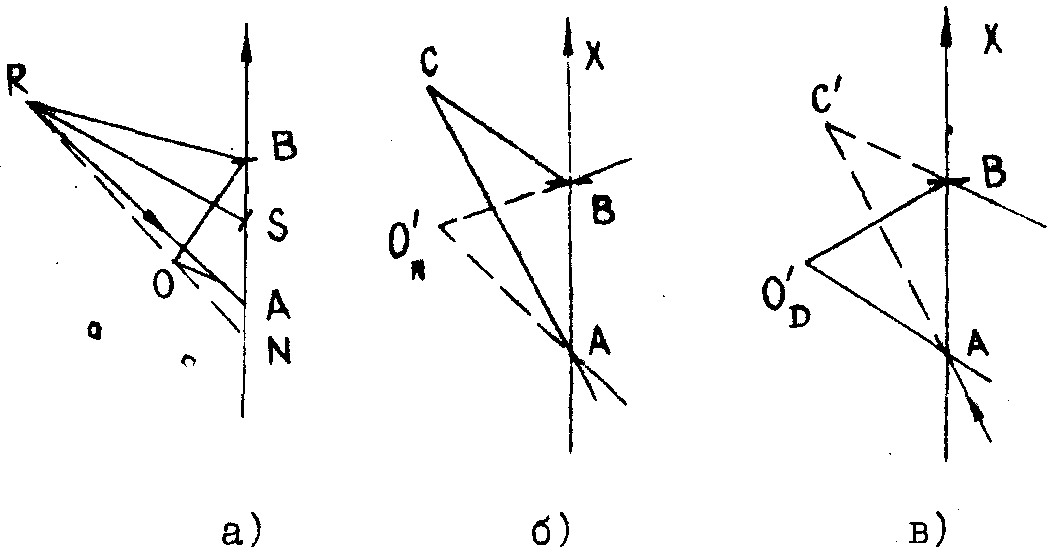
Рис.1. Схема записи и восстановления при расположении объекта и опорного источника с одной стороны голограммы. При восстановлении действительного изображения необходимо осветить голограмму обращённым пучком, т.е. сходящимся вблизи той точки, где находился опорный источник. Дифракционная решетка голограммы работает на пропускание.
а) Схема записи, б) Восстановление мнимого изображения, в) Восстановление действительного изображения.
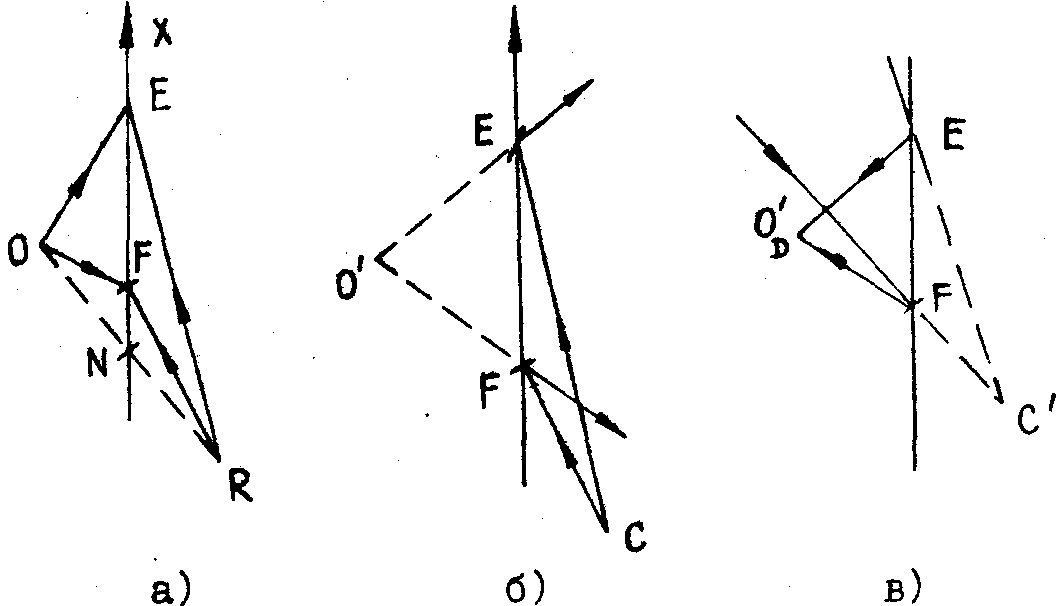
Рис.2. Схема записи и восстановления при расположении объекта и опорного источника с разных сторон голограммы. При восстановлении действительного изображения требуется обращение восстанавливающего пучка. Дифракционная решётка голограммы работает на отражение.
а) Схема записи, б) Восстановление мнимого изображения. в) Восстановление действительного изображения.
- 305 -
В точке А углы a
0 - объектного луча и a
r - опорного луча почти равны. Здесь объектный и опорный волновые фронты как бы догоняют друг друга. Поэтому величина 1/d близка к нулю. Очевидно. недалеко от точки А на голограмме есть особая точна N, где 1/d точно обращается в нуль.
При перемещении по голограмме от точки А в направлении к точке S (где a
0-a
r=max) частота полос нарастает до наибольшего значения
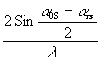
При движении к точке В угол
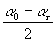 убывает
и частота полос поперёк биссектрисы падает. В точке Е биссектриса почти параллельна
плоскости голограммы, и частота полос поперёк биссектрисы невелика. При движении
к точке F
частота полое возрастает, пока в точке
N не достигает максимума. Здесь волновые
фронты движутся навстречу, а частота интерференционной картины вдоль лучей 2/l
, так как a r=p
+a 0.
убывает
и частота полос поперёк биссектрисы падает. В точке Е биссектриса почти параллельна
плоскости голограммы, и частота полос поперёк биссектрисы невелика. При движении
к точке F
частота полое возрастает, пока в точке
N не достигает максимума. Здесь волновые
фронты движутся навстречу, а частота интерференционной картины вдоль лучей 2/l
, так как a r=p
+a 0.
Однако для описания воздействия интерференционной структура на падающий луч нам важно знать не вообще частоту этой структуры, а лишь частоту дифракционной решетки, которую встречает падающий луч. Дифрагирующая сила j
описывает поворот луча в данной точке решетки в первый и последующие дифракционные порядки (мы ограничимся только первым порядком).
Для тонкой эмульсий, имеющей толщину менее длины волны, дифрагирующая сила, обусловленная интерференцией двух пучков, равна:
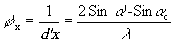
где a
'x - постоянная дифракционной решётке вдоль оси х на поверхности голограммы, a
с - угол восстанавливающего луча с нормалью к поверхности голограммы, a
' - угол восставленного луча. Таким образом, отличие этих двух терминов в их происхождении, охвате различных сторон физических явлений и в области использования.
- 306 -
Интерференционные полосы, характеризуемые частотой, возникают при наложении волновых полей. Дифрагирующей силой может обладать любая структура, не обязательно интерференционного происхождения. Это могут быть рисованные штрихи дифракционной решетки или какие-то дефекты голограммы. Термин "дифрагирующая сила" используется в геометрической оптике голограмм при построении лучей, дающих восстановленное изображение. (Аналогично в линзовой оптике для построения изображения можно было бы ввести "преломляющую силу" линзы в каждой ее точке. Однако употреблений этого термина удалось избежать, так как из-за высокой симметрии линзовых систем были введены более общие параметры.) В настоящей работе дифрагирующая сила не учитывает ту часть интерференционной структуры, которая не даёт вклада в нужное изображение. Так, если нам нужно построить качественное действительное изображение, то условия для построения качественного мнимого изображения обычно не выполнены. Поэтому та часть интерференционной структуры, которая дает вклад в искаженное мнимое изображение для построения действительного изображения не представляет интереса. Другими словами, мы будем считать, что дифрагирующая вяла описывает ту дифракционную решетку, которую "видит" волна источника при приближении к голограмме и которая поворачивает луч при восстановлении в направлении нужного изображения.
Далее нас будет интересовать лишь положение и качество восстановленного действительного изображения. Будем считать, что запись голограммы производится по схеме на рис.1 (источник и объект слева от голограммы) опорным пучком, сходящимся в точку R справа от голограммы. Восстановление производим пучком, расходящимся из точки С вблизи точки R. Тогда вблизи точки О' возникает действительное изображение точки О. Наша задача - найти положение и аберрации восстановленной точки.
По этой схеме записи в точке N дифрагирующая сила j
=0. Поэтому точка N называется нулевой точкой, а линия, соединяющая R и О, С и О', называется осевой линией.
В схеме с обращённым опорным пучком (рис.2) голограмма строит изображение на отражение. Вблизи точки Е интерференционные
- 307 -
плоскости почти параллельны поверхности голограммы (a
r»
p
-a
0) и дифрагирующая сила очень мала. При движении к точке N она достигает значения
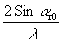
В схеме с обращенным опорным пучком по толщине эмульсии образуется несколько интерференционных слоев, и эмульсию уже нельзя считать тонкой, так как при восстановлении изображения надо учитывать интерференционные эффекты. Эта схема здесь не рассматривается.
4. Теория построения голографического изображения
Каждая зона голограммы "реагирует" только на кривизну падающей волны 1/r
и угол a
между касательной к фронту и поверхностью голограммы. И, наоборот, положение зонной точки изображения определяется кривизной восстановленной из этой зоны волны и наклоном касательной к фронту этой волны.
Используя эти параметры, получим общие формулы, позволяющие определить положение изображения, восстановленного из каждой зоны голограммы. Понятно, что в общем случае разные зоны голограммы формируют изображение точки в равных участках пространства. Задачей геометрической оптики голограмм является сведение этого разброса изображающих точек до допустимого уровня, задаваемого требуемым разрешением голографического изображения.
Итак, пусть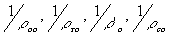 - кривизны объектного, опорного, изображающего и восстанавливающего фронтов
в нулевой точке голограммы; a ro
и a co
- углы осевой линии с нормалью при записи
и восстановлении в нулевой точке;
- кривизны объектного, опорного, изображающего и восстанавливающего фронтов
в нулевой точке голограммы; a ro
и a co
- углы осевой линии с нормалью при записи
и восстановлении в нулевой точке; 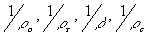 -соответствующие кривизны и a o,
a r,
a ',
a с
- углы соответствующих лучей с нормалью
в произвольной малой зоне вблизи точки голограммы. Обобщённые схемы записи и
восстановления показаны на рис.3 и 4.
Эти схемы охватывают все случаи получения
действительного и мнимого изображения, показанные на рис.1 и
2, когда лучи
-соответствующие кривизны и a o,
a r,
a ',
a с
- углы соответствующих лучей с нормалью
в произвольной малой зоне вблизи точки голограммы. Обобщённые схемы записи и
восстановления показаны на рис.3 и 4.
Эти схемы охватывают все случаи получения
действительного и мнимого изображения, показанные на рис.1 и
2, когда лучи
- 308 -
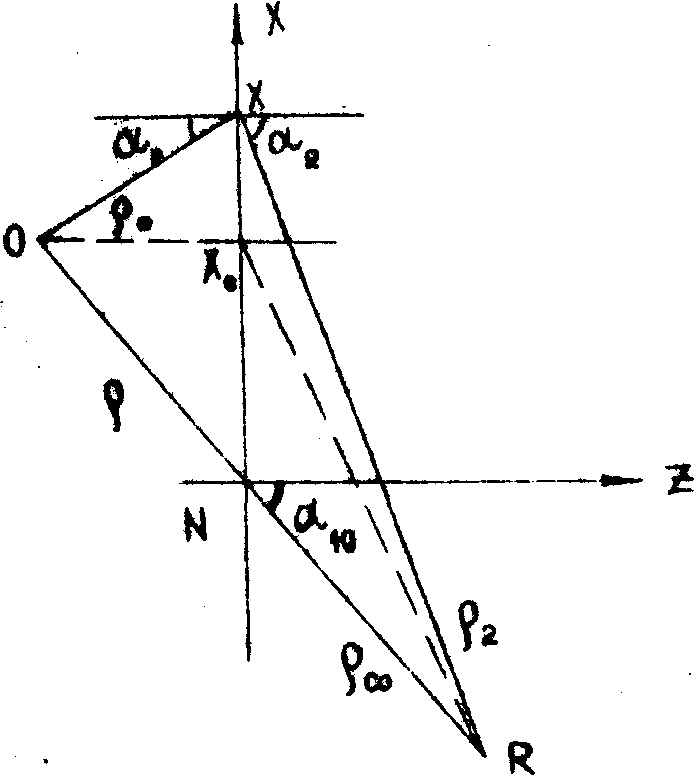
Рис.3. Обобщенная форма записи.
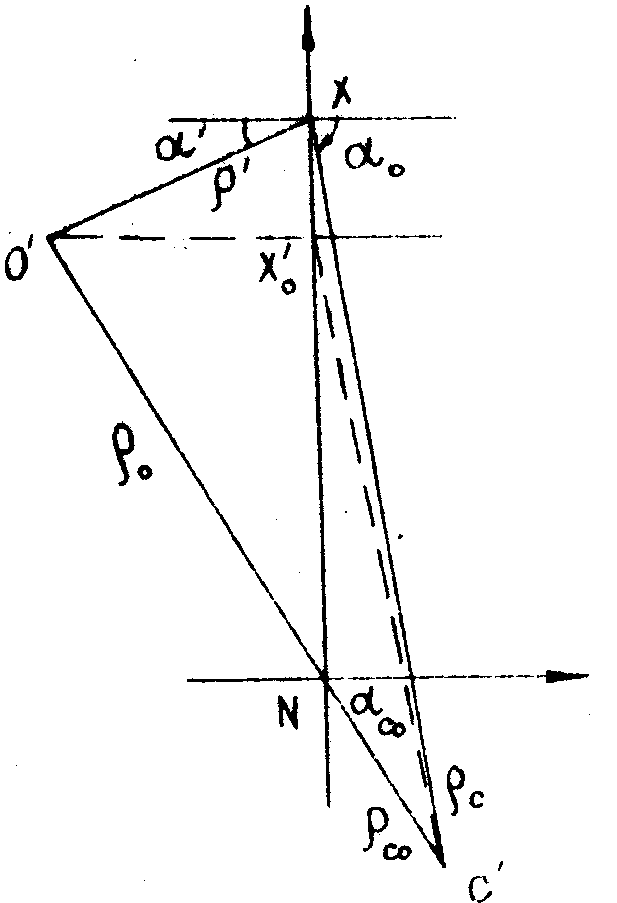
Рис.4. Обобщённая схема восстановления.
- 309 -
опорного и восстанавливающего источника сходятся или расходятся из точки справа от голограммы, хотя для целей технологии достаточно рассмотреть получение действительных изображений по схемам на рис.1a и 2в. Возможные схемы, когда объект и точка, из которой выходят или в которую сходятся лучи опорного источника, находятся по одну сторону голограммы, рассматриваются совершенно аналогично. Здесь, правда, возможен частный случай, когда нулевая точка уходит в бесконечность (схема Фурье). Этот случай для рассмотрения данным методом непригоден и рассматриваться нами не будет.
При построении зонального изображения О' мы предполагаем, что точка О' лежит на осевой линии, т.е. прямой линии, проведенной через точки С' и N. Нетрудно доказать, что это действительно так. Предположим, напротив, что точка О' не лежит на осевой линии С'N. Тогда поместим в эту точку источник и проведем осевую линию через О' и С'. Теперь осевая линия будет проходить через другую точку N' голограммы. Однако в плоскости голограммы имеется только одна точка, не обладающая дифрагирующей силой. Противоречие доказывает правильность предположения.
Будем считать все углы, отсчитываемые от нормали против часовой стрелки, положительными, по часовой - отрицательными. Дифрагирующая сила при записи в произвольной точке (без учёта показателя преломления регистрирующей среды)
 (1)
(1)
При восстановлении в той же точке голограммы
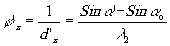 (1)
(1)
Заметим, что величина дифрагирующей силы не зависит от среды. (Хотя длина волны в среде укорачивается в n раз, но и углы с нормалью по закону Снелла уменьшаются во столько же раз, что обеспечивает сохранение размеров интерференционных полос). Будем считать, что l
1=l
2 и d'x=dx, т.e. зарегистрированная
- 310 -
интерференционная картина в направлении х мало отличается от "эфирной". Последнее обычно справедливо, поскольку регистрирующая среда в этом направлении не имеет степеней свободы. Например, фотоэмульсия имеет усадку по толщине в направлении оси z, а вдоль поверхности рельеф закреплён жёстко из-за наличия связующей стеклянной подложки. Будем считать голографическую дифракционную решётку плоской, хотя это выполняется лишь приближённо при dz<l
. Тогда имеем:
Sina
'-Sina
o = Sina
o-Sina
r (3)
Сравнивая треугольники NOX и NO'Х, по формуле синусов находим:
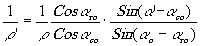 (4)
(4)
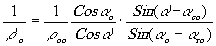 (5)
(5)
Формула (4) представляет наиболее общее выражение для кривизны восстановленного фронта. Формулы (3) и (4) или (3) и (5) полностью определяют положение точки, восстановленной путём дифракции на участке голограммы, расположенном вблизи точки х. Достаточно на луче, идущем под углом d', отложить отрезок r
' или на нулевой линии NC' отложить отрезок r
'o. Сравнивая треугольники NRX и NC'X, находим
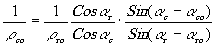 (6)
(6)
Сравнивая треугольники NO'X и NС'X, получаем
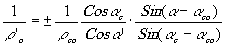 (7)
(7)
Здесь верхний знак берётся при a
c<a
co, нижний при a
c>a
co.
Качество восстановленного изображения можно охарактеризовать разбросом значений r
'o вдоль нулевой линии NC'.
- 311 -
D
r
= r
'omax-r
'omin (8)
где r
'omax соответствует точке голограммы, восстанавливающей наиболее удалённое от N изображение, r
'omin - наиболее близкое изображение. Обычно это две крайние точки голограммы, если нулевая точка не попадает на фотоэмульсию.
Для нулевой точки r
'o отсутствует, поэтому в схеме Габора за меру разброса можно брать (так как a
oo=a
ro)
D
r
' = r
'omax-r
oo (8a)
Для более корректного определения размытия восстановленной точки необходимо построить каустические поверхности и вычислить размеры их сечений (обычно в плоскости параллельной голограмме).
Рассмотри частные случаи.
1. Геометрия записи полностью сохранена при восстановлении.
r
co=r
ro; a
co=a
ro; a
c=a
r; a
'=a
o
Будем считать в этом случае, что фокусное расстояние голограммы равно бесконечности, тогда срезу получаем
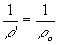
2. Схема Габора.
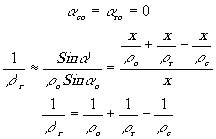 (9)
(9)
Здесь фокусное расстояние зависит только от кривизны опорного
и восстанавливающего пучков 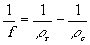
- 312 –
Для расстояний вдоль оси:
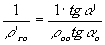 (10)
(10)
При a
'<<1 и a
o<<1 (но a
o¹
1) получаем известную формулу фокуса зонной пластинки Френеля. Нетрудно видеть, что и общем случае голограмма Габора даёт сильные сферические аберрации, так как разброс вдоль и поперёк оси, соответственно,
D
r
= r
oo-r
'го ¹
0 (11)
D
x = D
r
tga
' = r
oo(tga
'-tga
o) (12)
Аберрации отсутствуют лишь при a
'=a
o.
3. Схема Габора с голограммой, наклонённой под углом a
ro к оси (нулевой линии OR), рис.5. Голограмма расположена вблизи нулевой точки. Восстанавливающий пучок смещен вдоль оси.
a
co = a
ro
a
o = a
ro-D
a
o; a
' = a
ro-D
a
';
a
r = a
ro-D
a
r; a
c = a
ro-a
c
Для всех D
a
: SinD
a
»
D
a
, из формулы (3)
D
a
' = D
a
o-D
a
r+D
a
c (13)
- 313 -
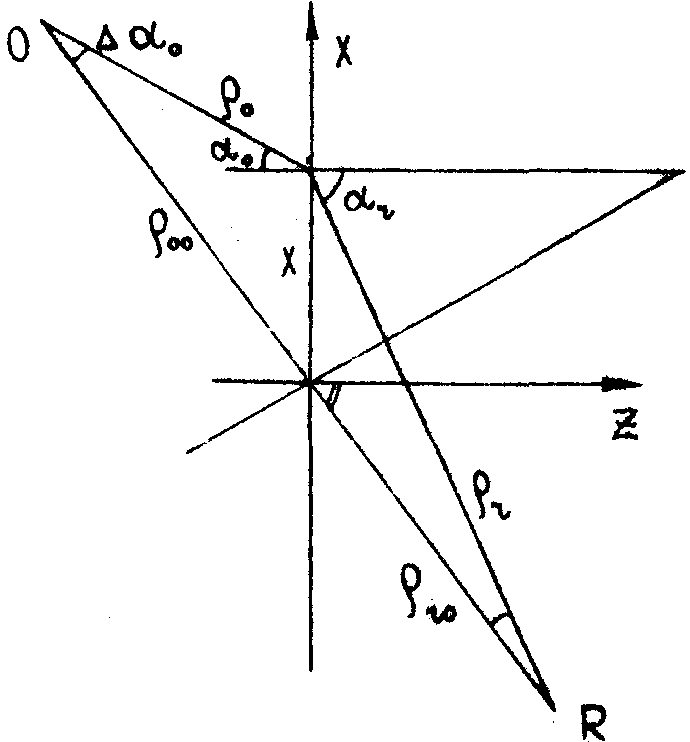
Рис.5. Схема Габора с голограммой, наклонённой к оси.
Из формул (4) и (5) получаем:
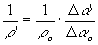 (14)
(14)
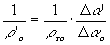 (15)
(15)
Так как из рисунка 5 и формулы синусов:
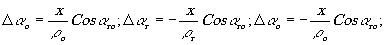 (16)
(16)
то
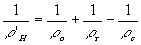 (17)
(17)
- 314 -
В отличие от формулы (9) последняя справедлива лишь в параксиальной области
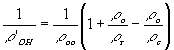 (18)
(18)
Из этих выражений видно, что аберрации в восстановленном изображении отсутствуют только при сохранении геометрии записи на этапе восстановления.
4. Схема Габора при записи. Восстанавливающий источник смещён по нормали к оси на расстояние ℓ (рис.6)
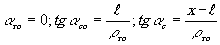 (19)
(19)
Из формул (4) и (5) получаем
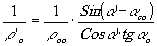 (20)
(20)
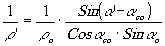 (21)
(21)
Найдём величину отрезка МР, характеризующего размеры восстановленного изображения точки в плоскости МО. Из подобия треугольников MPO'и O'ХN находим:
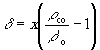 (22)
(22)
Отсюда, используя (19) и (20), получаем:
d
= r
ro(tga
'+tga
r-tga
co) (23)
Здесь угол a
' определяется из условия (4).
Рассмотрим частный случай этой формулы, полезный для определения разрешения изображения при мультиплицировании ℓ<<r
ro.
- 315 -
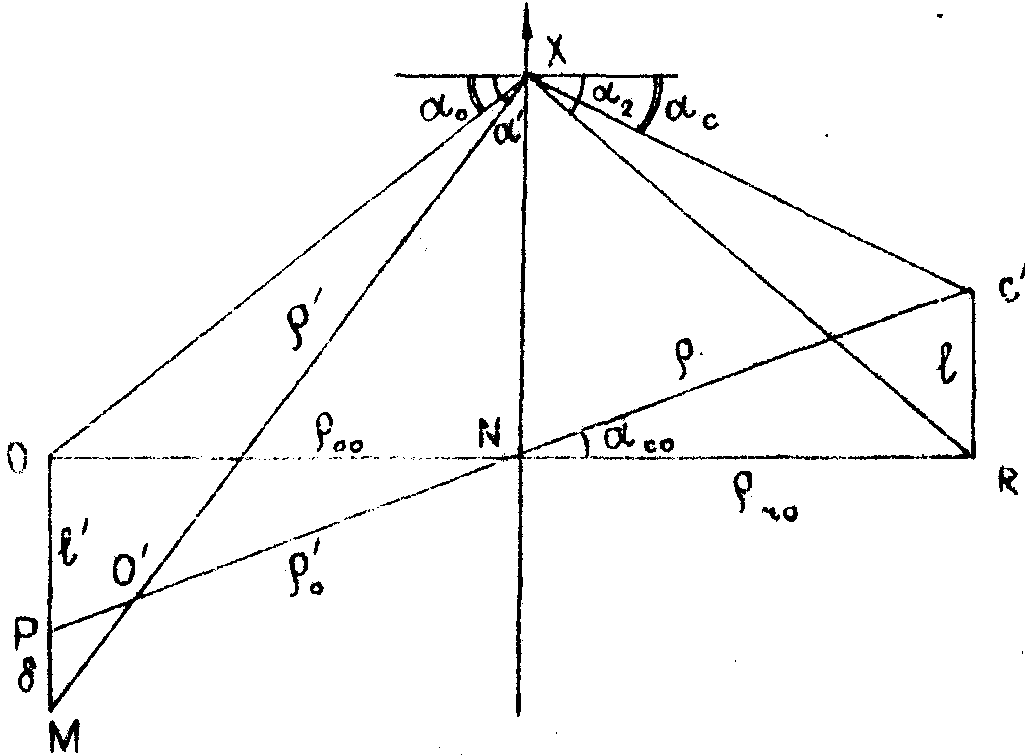
Рис.6. Схема Габора со смещением восстанавливающего источника по нормали к оси.
Здесь обычно
r
oo = r
ro; a
o = a
r
Тогда
a
с = a
o-D
a
; a
' = a
с+D
a
; D
a
<<1
Из треугольника C'XP находим по формуле синусов
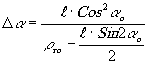 (24)
(24)
Тогда, преобразуя формулу (23), получаем
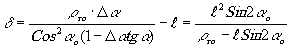 (25)
(25)
- 316 -
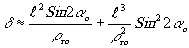 (26)
(26)
Если мы хотим использовать эту формулу для определения разрешения в восстановленном изображении, то необходимо брать
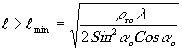 (27)
(27)
Это условие связано с тем, что разрешение изображения не может быть выше дифракционного предела Sina
0/l
. Отсюда диаметр поля, на которое обеспечено дифракционное разрешение,
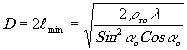 (28)
(28)
значительно превышает размер первой зоны Френеля лишь при малых апертурах (dо<<1).
5. Схема для получения протяжённых изображений с разрешением на дифракционном пределе. Объект и изображение расположены близко к голограмме (рис.7). Голограмма расположена в районе точки хо. Чтобы не задеть изображение восстанавливающим пучком, необходимо подавать его и опорный пучок под очень большим углом.
a ro = b
ro-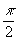 так как
a ro<0
так как
a ro<0
a co = b
co-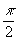
Будем считать также
r
co = r
ro = ¥
; a
' = a
o-D
a
; D
a
<<1
a
ro-a
co = b
ro-b
co = D
b
где D
b
<<1
- 317 -
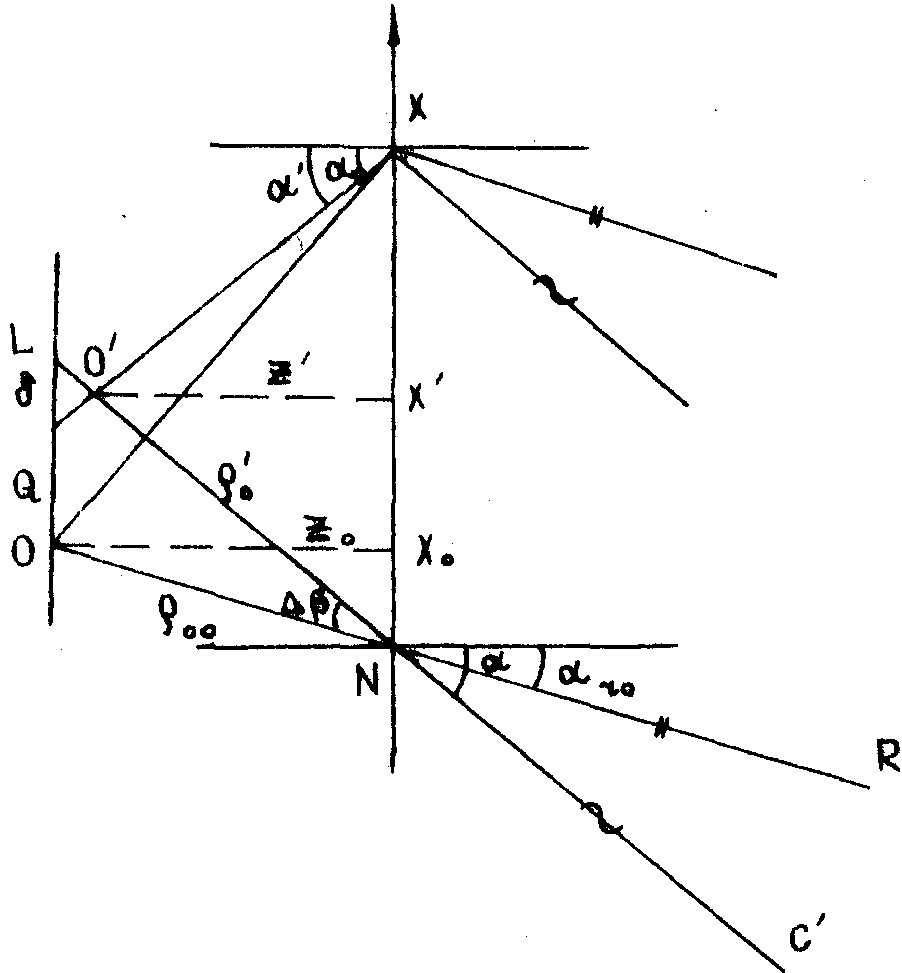
Рис.7. Схема записи и восстановления с параллельным пучком.
Тогда a
r=a
ro; a
c=a
co, и из формулы (4) имеем:
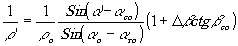 (29)
(29)
Для приближённой оценки размера d
точечного изображения вычислим величину отрезка LQ в плоскости, проходящей через O и параллельной голограмме. Будем считать именно её плоскостью изображения, хотя размер сечения каустической поверхности в плоскости, несколько отличной от проходят и через LQ, может быть несколько меньше d
.
Из подобия треугольников LQO' и ХNO' получаем
- 318 -
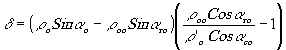 (30)
(30)
Выразим d
через угол D
b
доворота, необходимого, например, из-за усадки эмульсии:
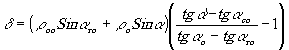 (30)
(30)
Учтём теперь, что
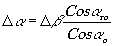 (32)
(32)
Тогда несложные преобразования дают при b
ro→0, D
b
<<b
ro.
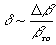 (33)
(33)
Таким образом, при приближении объекта к голограмме и очень наклонном падении опорного пучка даю незначительные довороты будут полностью деградировать восстановленное изображение.
Предположим теперь, что регистрирующая среда имеет показатель
преломления n>1. Обычно
для желатины n=1,5. Тогда
даже при b ro→0
угол преломлённого луча с поверхностью среды
r→arccos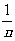 . На
самом деле аберрации будут обусловлены дифракцией на решётке, образованной в
среде под углом r¹
0
. На
самом деле аберрации будут обусловлены дифракцией на решётке, образованной в
среде под углом r¹
0
З а к л ю ч е н и е
Голография открывает уникальную возможность создавать короткие (негауссовы) оптические системы. Для их описания непригодны известные методы гауссовой оптики. Однако голографические системы обладают рядом характерных свойств, на основе которых возможно построение геометрической оптики коротких голографических
- 319 -
систем.
1. Голограммы (кроме голограмм Фурье) имеют оптическую ось - осевую линию. Пересечение осевой линии с голограммой даёт нулевую точку, в которой поворот дифрагированного луча относительно восстанавливающего отсутствует или равен 180°.
2. На голограмме для каждой точки объекта можно выделить "парциальную" голограмму - результат интерференции света от опорного источника и этой точки объекта. Голограмма не строит изображения. как линза. Вместо этого при восстановлении "парциальная" голограмма концентрирует часть светового излучения восстанавливающего источника в район вблизи расположения одной точки - точки изображения.
5. Каждая зона голограммы обладает определённой дифрагирующей силой, т.е. способностью повернуть упавший на неё луч (хотя в реальной голограмме действующая дифрагирующая сила может отличаться от "эфирной").
На основе использования этих свойств получены формулы, описывающие положение зональных изображающих точек (восстановленных путём дифракции на любой из зон голограммы). Разброс положения зональных точек обуславливает величину аберраций восстановленного изображения.
Показано, что в принципе голография позволяет создать идеальную оптическую систему, т.е. систему без аберраций, причём разрешение в каждой точке изображения будет определяться только апертурой голограммы относительно этой точки и в предельном квазиконтактном случае приближаться к 0 . Практически это означает, что средствами голографии можно создать предельное разрешение по полю существенно больших размеров, чем у лучших линзовых систем. Преимущества голографии становятся тем ощутимее, чем выше требуется апертура и больше размеры поля. Если схемы голографирования и восстановления выбраны правильно, то погрешности изображения обусловлены только качеством осветительных коллиматоров и фотоэмульсии.
- 32O -
Основное требование к схеме восстановления - сохранение геометрии записи. Ввиду усадки эмульсии и неравномерности усадки сохранить геометрию не всегда удаётся. Тем не менее, даже при приблизительном сохранении геометрии возможна не очень существенная деградация изображения. Чем выше требуемое разрешение в изображении, тем больше необходимо приложить усилий по сохранению геометрии.
- 321 -
Л и т е р а т у р а
1. R.W.Meier. J.Opt.Soc.Amer., 56, 2, 219-223 (1966).
2. F.Bestenreiner, R.Deml. Z.Angev. Physic, 25, 4, 243-249 (1968).
3. S.N.Butters, D.Denby, J.A.Leenderts. J.Sci.Instrum., ser.2, 2, 1. 116-118 (1969).
4. A.Offner. J.Opt.Soc.Amer., 56, 11509-1512 (1966).

