- 273 -
КОГЕРЕНТНЫЕ МЕТОДЫ АНАЛИЗА СТРУКТУРЫ ИЗОБРАЖЕНИЙ
А.С.Островский
В в е д е н и е
Здесь будут рассмотрены некоторые методы пространственной Фильтрации изображения, которые могут оказаться полезными при решении таких сложных задач технической кибернетики как ввод в ЭЦВМ и кодирование оптических сигналов /1/, машинная интерпретация сложных изображений /2-4/ распознавание визуальных образов /5,6/ и т.д.
В последние годы наметился новый перспективный подход к решению перечисленных задач, основанный на структурном анализе изображений /2,5,6/. Вкратце этот подход заключается в том, что изображение расчленяется на элементарные части (элементарные структуры), затем производится его автоматическое описание в терминах этих элементарных структур. В работах /2,5,6/ в качестве таких элементарных структур были выбраны направленные прямые линии и линии малой кривизны, а также характерные точки изображения - точки пересечения, угловые точки, концевые точки, углы и т.д. Следует указать, что такой выбор хорошо согласуется с данными электрофизиологических экспериментов, целью которых было выяснение отдельных механизмов восприятия изображений высокоорганизованными организмами, в том числе и человеком /7,8/.
Коротко остановимся на возможных технических средствах решения задачи анализа структуры изображения. Поскольку оптическое изображение по своей природе является функцией двух независимых переменных, (пространственных координат х и у), решение задачи анализа его структуры средствами электроники, оперирующими с функциями одной независимой переменной (времени), приводит к необходимости использовать дополнительные устройства –
- 274 -
строчную развертку, сетчатку из фотоэлементов и т.д. Среди электронных устройств, решающих задачу анализа структуры изображений, пожалуй, наибольшее предпочтение следует отдать сетям из искусственных нейронов /5,6/ и ЭЦВМ /2/. Однако и они не лишены существенных недостатков. Реализация устройств из искусственных нейронов сопряжена со значительными трудностями технического, а зачастую н принципиальною характера. Анализ структуры изображения с использованием ЭЦВМ протекает относительно медленно, так как вычислительная машина производит обработку данных последовательно во времени.
Очевидно, наиболее подходящими (с точки зрения адекватности операнда и оператора) методами анализа структуры изображения следует признать оптические методы, поскольку оптические системы так же, как и изображение, обладают двумя степенями свободы (х и у) /9/.
Прежде чем перейти к рассмотрению оптических методов анализа структуры изображений, необходимо хотя бы вскользь коснуться основных положений пространственной фильтрация.
1. Основные положения пространственной фильтрации
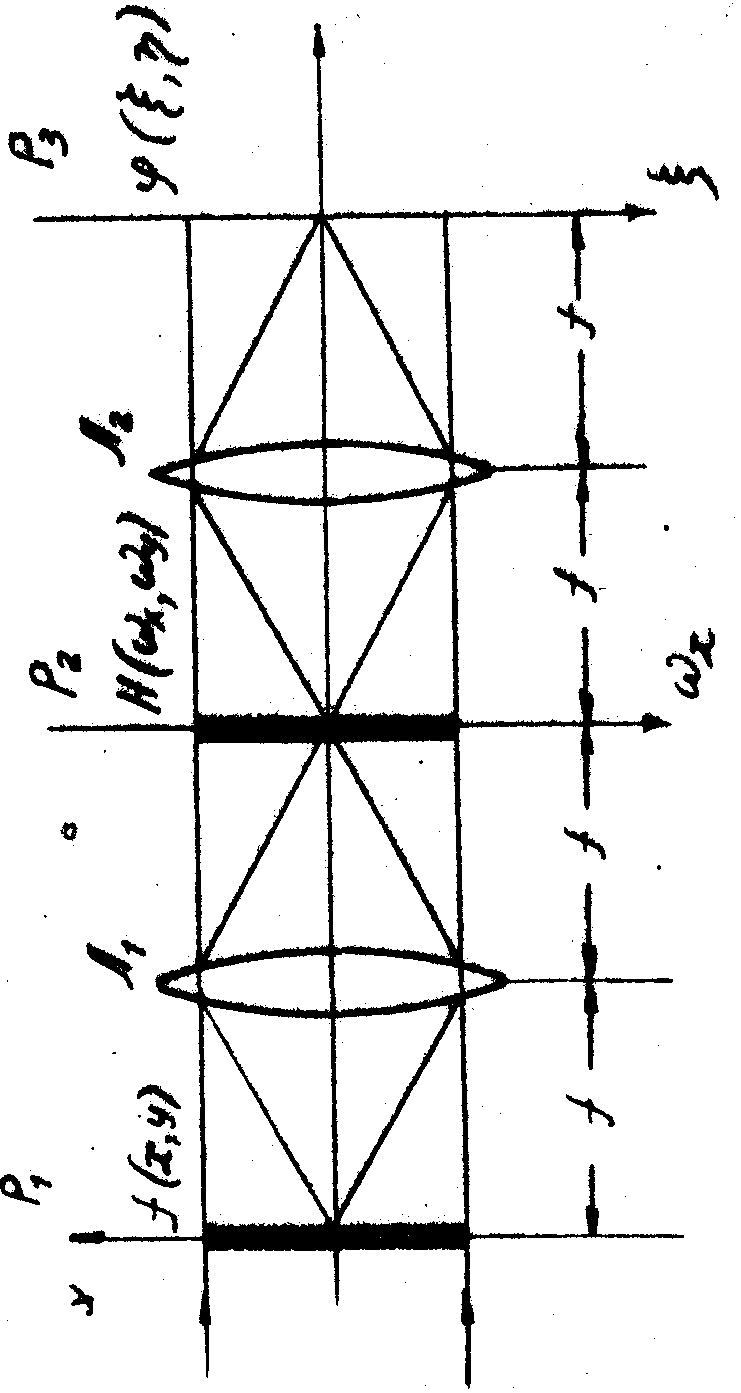
Рассмотрим оптическую систему, изображённую на рис.1. В задней фокальной плоскости линзы L
1(P1) устанавливается транспарант с пропусканием ¦
(x,у), который освещается плоскопараллельным монохроматическим когерентным лучом. Как известно, /10/ линза L
1 осуществляет двумерное Фурье-преобразование распределения ¦
(х,у). Таким образом, в частотной плоскости Р2 (передняя фокальная плоскость линзы L
1) имеем Фурье-спектр
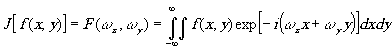 (1)
(1)
В плоскости P3 происходит перемножение Фурье-спектра /1/ на пропускание транспаранта Н(w
х,w
у), представляющее собой частотную характеристику пространственного фильтра.
- 275 -
- 276 -
В передней фокальной плоскости линзы Л (выходной плоскости Р- ) инеем распределение
J[F(w
x,w
y)×
H(w
x,w
y)] (2)
которое, согласно обратной теореме о свертке, можно переписать в виде*;
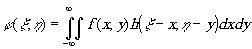 (3)
(3)
Выражение (3) представляет собой интеграл свёртки фильтруемого сигнала ¦
(х,у) и весовой функции фильтра h(x
,h
), которая определяется как инверсный Фурье-образ частотной характеристики фильтра:
h(x
,h
) = J-1[H(w
x,w
y)] (4)
Если в частотной плоскости Р2 фильтр отсутствует, то в выходной плоскости Р3 имеем распределение
J[F(w
x,w
y)] = ¦
(x
,h
) (5)
т.е. перевёрнутое действительное изображение ¦
(-х,-у).
Теперь переходим к непосредственному рассмотрению основного вопроса лекции - анализу структуры изображений с помощью пространственных фильтров. Вначале рассмотрим простые бинарные фильтры, используемые для этой цели.
2. Бинарные пространственные фильтры /11/
Бинарным пространственным фильтром будем называть такой пространственный фильтр, частотная характеристика которого представляет собой действительную функцию двух переменных (w
х,w
х), принимающую только два значения 0 или 1.
* Переход от (2) к (5) был выполнен на основании предположения, что весовая функция h(x
,h
) - симметричная относительно начала координат, т.е. h(x
,h
)=h(-x
,-h
).
- 277 -
Изотропным бинарным фильтром будем называть фильтр с частотной характеристикой
H(w
x,w
y) = Н(r
) (6)
где
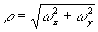
В противном случае бинарный фильтр будем называть анизотропным.
Рассмотрим основные типы бинарных изотропных фильтров.
1. Бинарный фильтр низких частот имеет частотную характеристику (рис.2а):
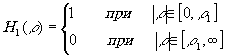 (7)
(7)
т.е. пропускает только те спектральные составляющие фильтруемого сигнала, у которых
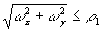
Весовая функция бинарного фильтра низких частот показана на рисунке 2б и описывается (согласно выражении (4)) следующим выражением:
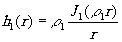 (8)
(8)
где 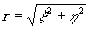 ,
а J1(r
1r) - функция Бесселя первого
рода первого порядка.
,
а J1(r
1r) - функция Бесселя первого
рода первого порядка.
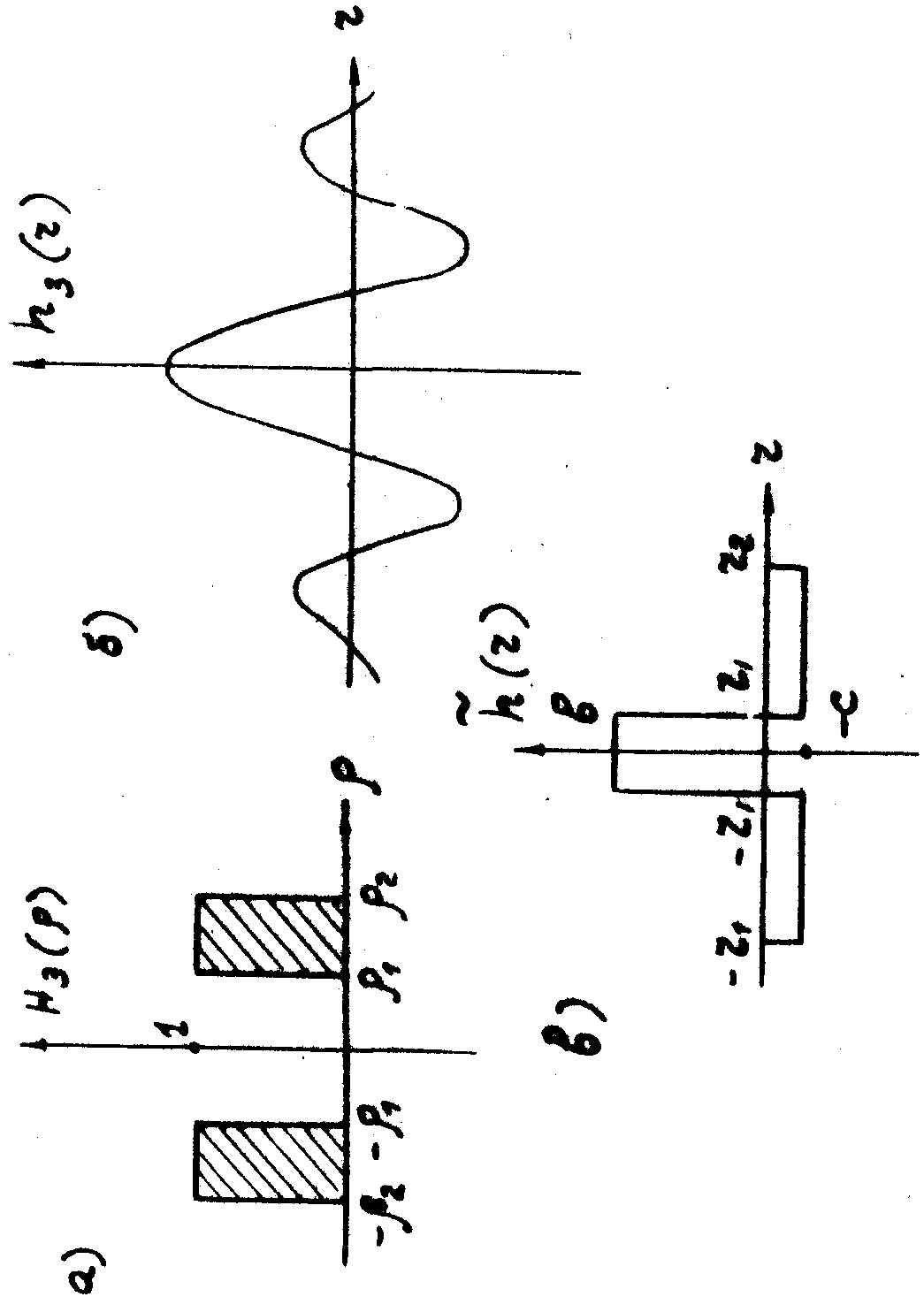
2. Бинарный фильтр высоких частот имеет частотную характеристику (рис.3а):
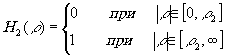 (9)
(9)
т.е. пропускает только те спектральные составляющие фильтруемого сигнала, у которых
- 278 -
- 279 -
- 280 -
 (10)
(10)
На рис.3б изображена весовая функция бинарного фильтра высоких частот:
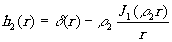 (11)
(11)
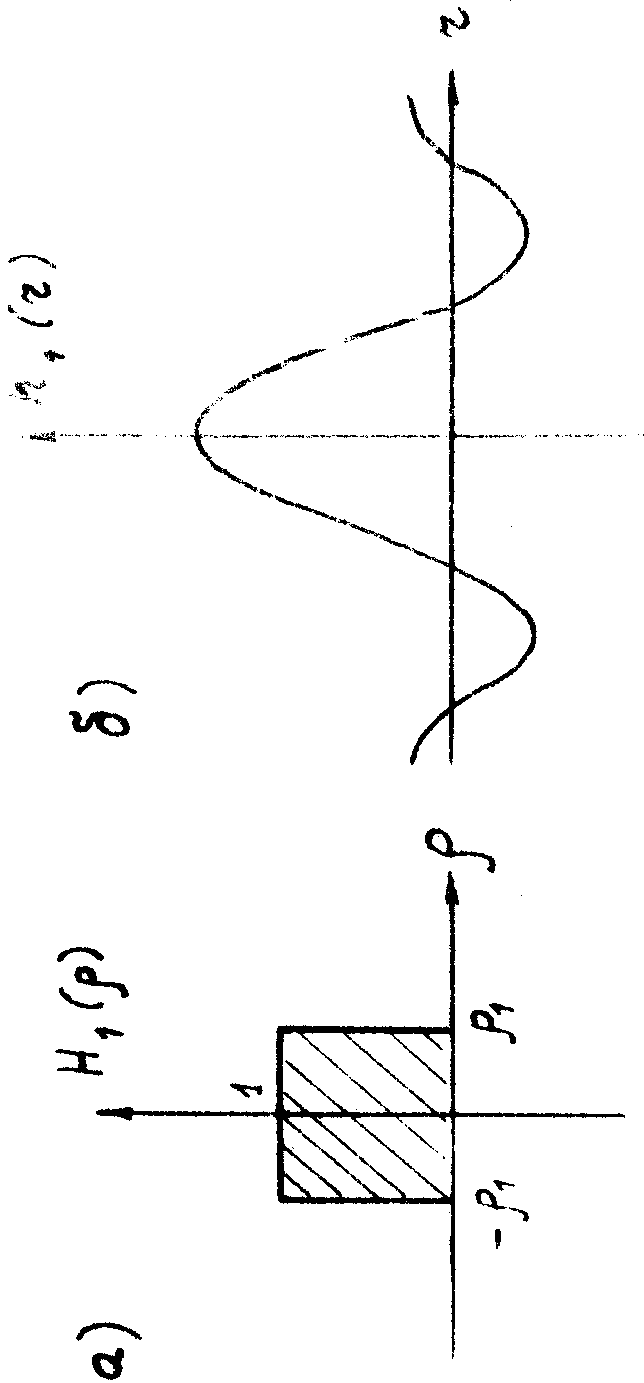
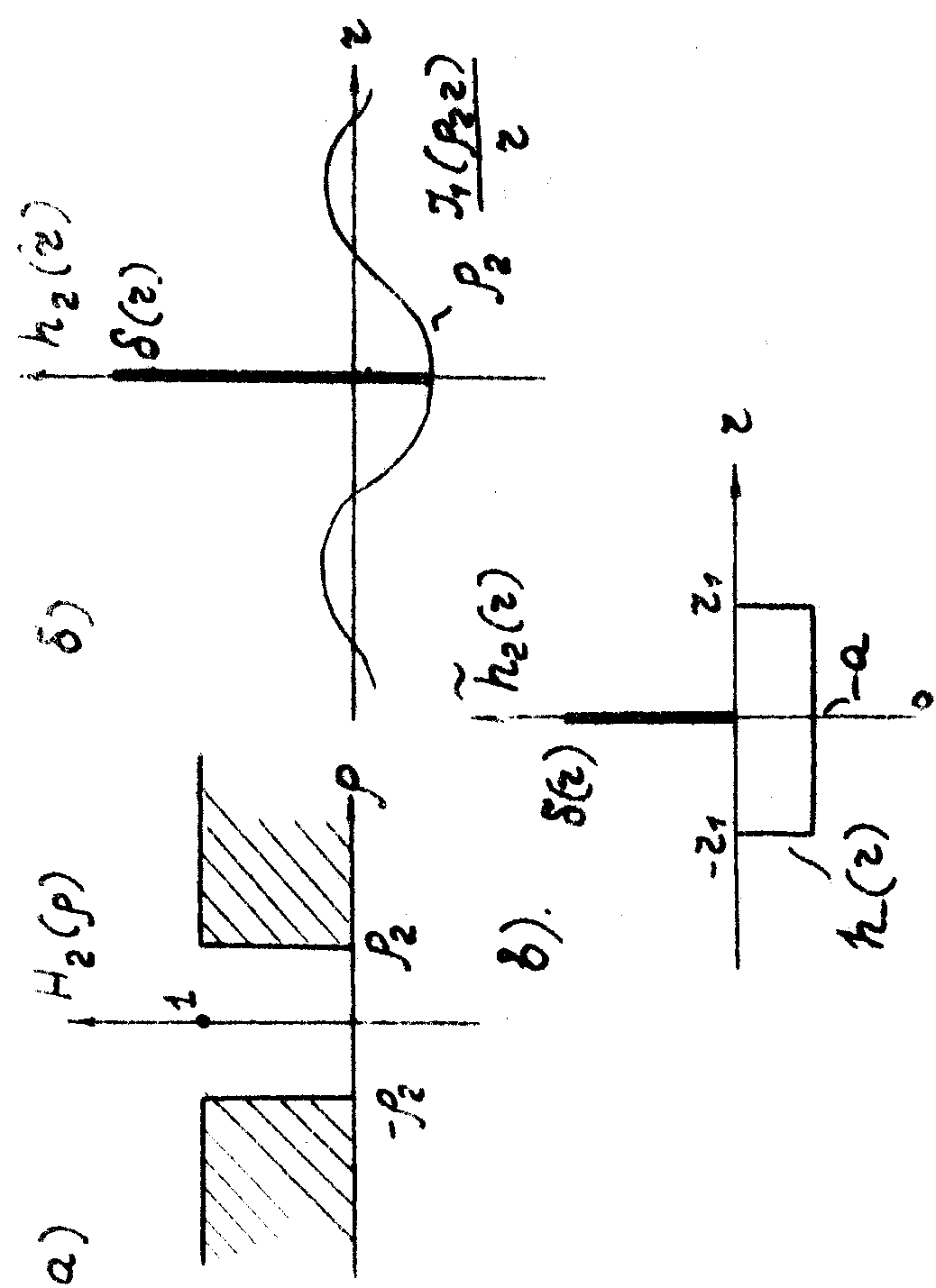
3. Бинарный полосовой фильтр пропускает только те спектральные составляющие фильтруемого сигнала, у которых
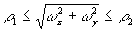 (12)
(12)
Его частотная характеристика (рис.4а):
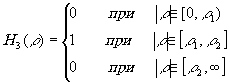 (13)
(13)
Весовая функция (рис.4б):
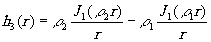 (14)
(14)
Заметим, что как у полосового фильтра, так и у фильтра высоких частот при w
х=0 и w
у=0
H(w
х,w
у) = 0 (15)
Мы знаем, что
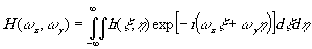 (1)
(1)
Из (15) и (16) следует, что
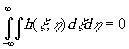 (17)
(17)
- 281 -
- 282 -
Так как h(x
,h
) - знакопеременная функция, то можно записать
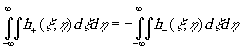 (18)
(18)
Аппроксимируем весовую функцию фильтра высоких частот /11/ следующим образом (рис.3в):
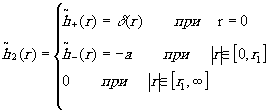 (19)
(19)
Тогда выражение (18) можно переписать в виде
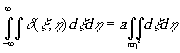 (20)
(20)
или
1 = аp
r12
откуда
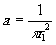 (21)
(21)
Причём параметр r1 определяется как первый нуль трансцендентного уравнения
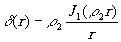 (22)
(22)
Если фильтруемый сигнал (изображение) - бинарный (принимающий значения 0 или 1), то интенсивность сигнала на выходе фильтра в точке (x
',h
'), согласно выражению (3), равна:
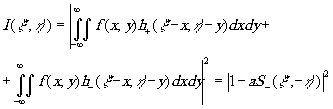 (23)
(23)
- 283 -
в случае, когда ¦
(х,у) перекрывает h+(x
'-x,h
'-y), и
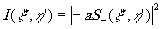 (24)
(24)
в противном случае.
В выражениях (23) и (24) S-(x
',h
') - площадь взаимного перекрытия ¦
(х,у) и h-(x
'-х,h
'-у).
На рис.5 показан процесс фильтрации бинарного изображения бинарным высокочастотным фильтром, причём выходной сигнал рассчитывался по формулам (23) и (24).
Итак, мы видим, что при соответствующем выборе параметра r1 (r1 - следует выбирать достаточно малым) высокочастотный бинарный фильтр производит оконтуривание изображения.
Теперь рассмотрим действие бинарного полосового фильтра. Покажем, что он производит акцентирование характерных точек изображения (точек пересечения, угловых точек и т.д.).
Для этого так же, как и в предыдущем случае, проведем аппроксимацию весовой функции полосового фильтра (рис.4в):
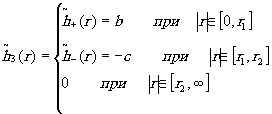 (25)
(25)
Нетрудно показать, что интенсивность сигнала на выходе фильтра в точке с координатами x
', h
' равна
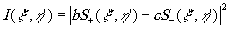 (26)
(26)
где S+(x
',h
') - площадь взаимного перекрытия ¦
(x,у) и h+(x
'-х,h
'-y), а S-(x
',h
') - площадь взаимного перекрытия ¦
(х,y) и h-(x
'-х,h
'-y).
Рассчитаем интенсивность выгодного сигнала в следующих типичных точках (рис.6а-г).
а) Весовая функция 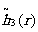 своим
центром лежит на пересечении линий, толщина которых равна
ℓ
(рис.6а). Выбираем параметр r1
таким, чтобы удовлетворялось неравенство
своим
центром лежит на пересечении линий, толщина которых равна
ℓ
(рис.6а). Выбираем параметр r1
таким, чтобы удовлетворялось неравенство
r1 >> ℓ (27)
- 284 -
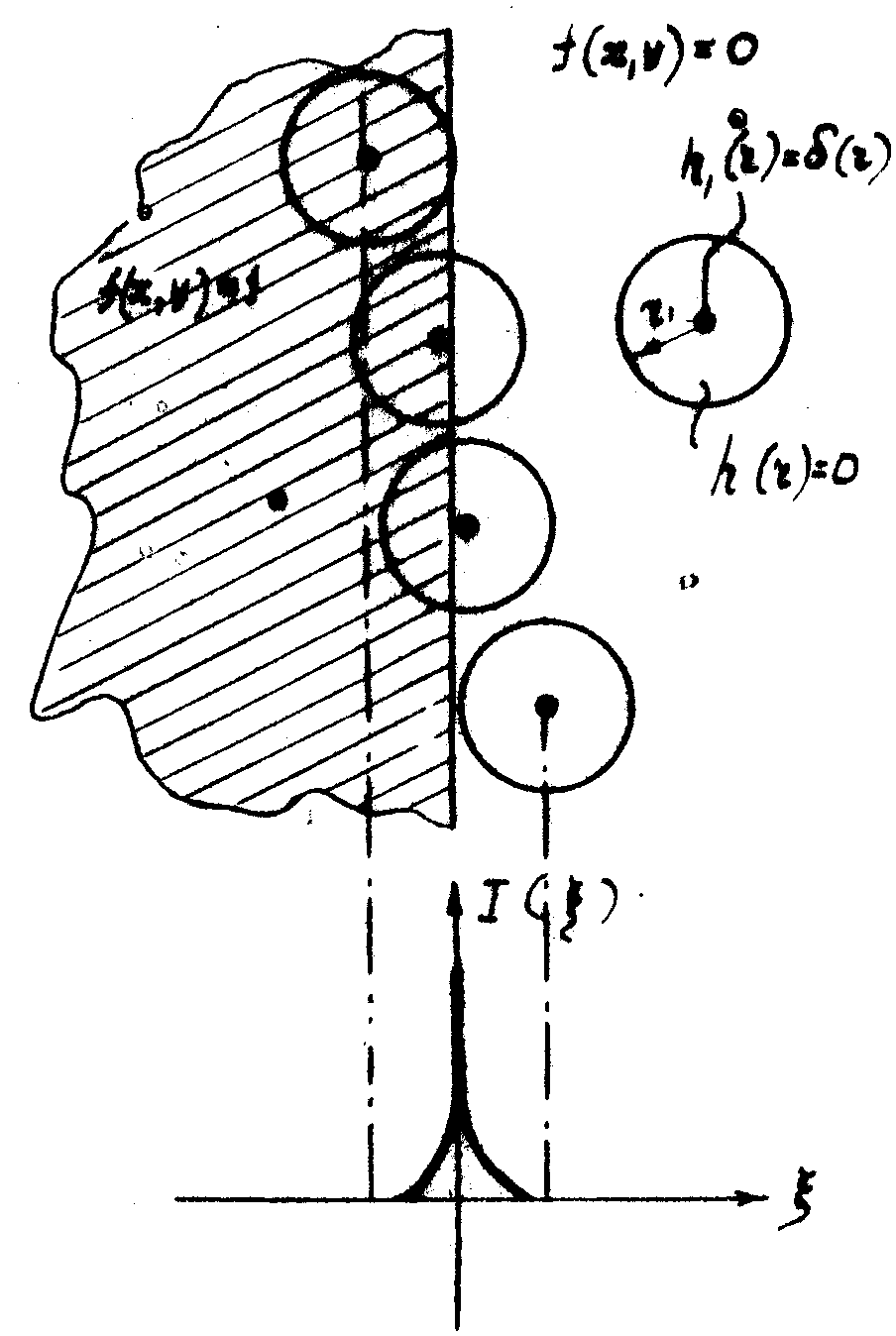
Рис.5.
- 285 -
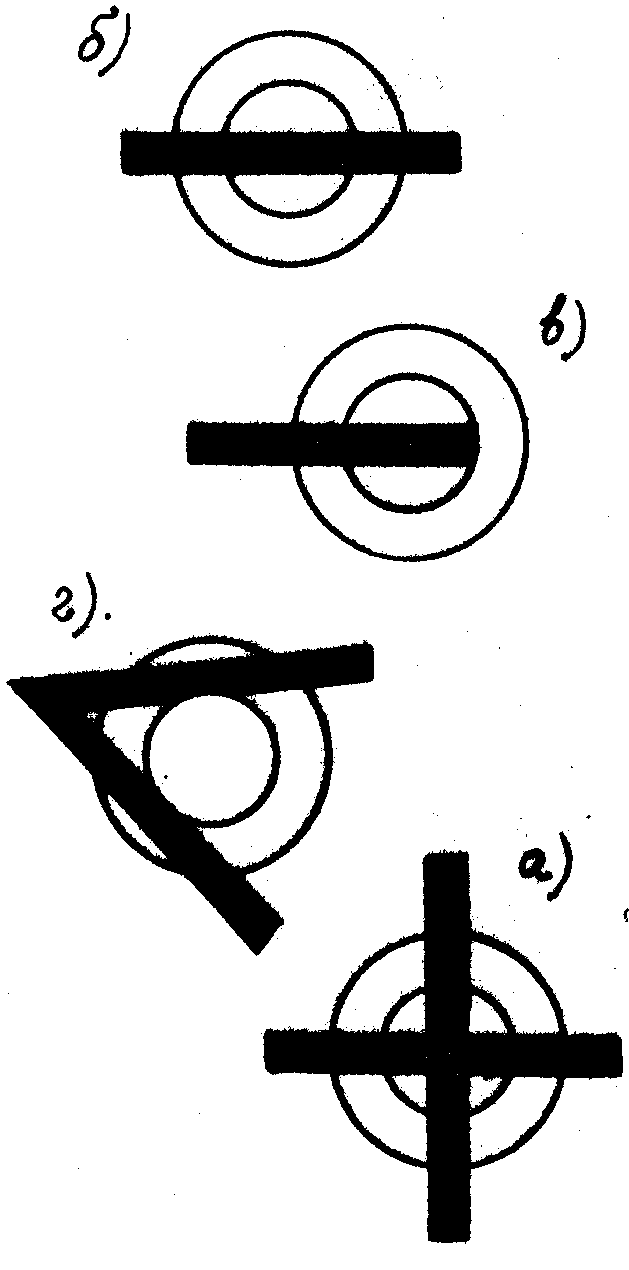
Рис.6.
- 286 -
Из (18) находим
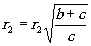 (28)
(28)
Тогда
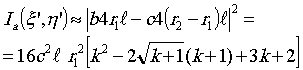 (29)
(29)
где k=b/c
б) Весовая функция  своим
центром лежит на линии (рис.6б):
своим
центром лежит на линии (рис.6б):
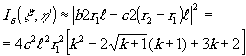 (30)
(30)
в) Весовая функция  своим
центром лежит на конце линии (рис.6в):
своим
центром лежит на конце линии (рис.6в):
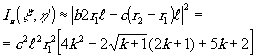 (31)
(31)
г) Центр весовой функции 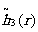 лежит
на диагонали угла, образованного двумя линиями (рис.6г):
лежит
на диагонали угла, образованного двумя линиями (рис.6г):
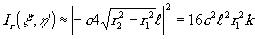 (32)
(32)
Сравнив попарно выражения (29)-(32), приходим к заключению, что, увеличивая параметр k, можно добиться сколь угодно большого превышения полезного сигнала (1а,1в) над вредными (1б,1г). Таким образом, приходим к заключению: бинарный полосовой фильтр при определённом выборе параметров может выделять характерные точки
- 287 -
изображения. Нетрудно убедиться в той, что аналогичный свойством обладает и низкочастотный фильтр.
Что же физически представляют собой описанные фильтры?
Низкочастотный бинарный фильтр изготавливается в виде непрозрачного экрана (фольга, латунь) с тонким проколом или сверлением в центре. Высокочастотный и полосовой бинарные фильтры изготавливаются фотоспособом: первый в виде прозрачного пятна, а второй - прозрачного кольца на тёмном, непрозрачном фоне. Примерную методику расчёта таких фильтров можно найти в работе /11/.
До сих пор мы рассматривали изотропные бинарные фильтры. Для выделения прямых линий и линий малой кривизны из контура изображения нам потребуется анизотропный фильтр.
Это очень хорошо видно из рис.7, где приведён спектр изображения, содержащего прямые линии различных направлений. Известно,

Рис.7.
- 288 -
что каждой прямой линии на изображении в частотной плоскости соответствует прямая линия, направленная перпендикулярно исходной и проходящая черва точку пересечения главной фокальной плоскости и оптической оси линзы, осуществляющей Фурье-преобразование. Отсюда ясно, что в качестве одного из возможных бинарных анизотропных фильтров, предназначенных для выделения ориентированных прямых линий и линий малой кривизны, может служить бинарная маска, представленная на рис.8. Причём угол в (рис.8) соответствует допустимому диапазону изменений направления линий, выделяемых данным фильтром.
На рис.9 показаны экспериментальные результаты по анализу структуры изображения с использованием описанных фильтров.

Рис. 8.
- 289 -

Рис. 9.
5. Голограммные фильтры
Мы видели, что физическая реализация бинарных пространственных фильтров чрезвычайно проста, однако наряду с этим несомненным достоинством они обладают и недостатками.
Во-первых, мы в известной степени идеализировали рассматриваемые
фильтры, поскольку весовые функции h(r)
значительно отличаются от аппроксимирующих их функций
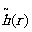 . Поэтому
и практические результаты фильтрации будут отличны от теоретических.
. Поэтому
и практические результаты фильтрации будут отличны от теоретических.
Во-вторых, использование пространственных фильтров с бинарной частотной характеристикой накладывает довольно жёсткие ограничения на выбор параметров оптимизируемой весовой функции. И, наконец, расчёт частотной характеристики фильтра по заданной (оптимизированной) весовой функции сопряжён с вычислительными трудностями - решением трансцендентных уравнений.
Поэтому можно предложить несколько отличный подход к выбору пространственных фильтров, предназначенных для анализа структуры изображения.
- 290 -
В качестве примера рассмотрим методику построения оптимального фильтра, выделявшего характерные точки.
Задаемся видом желаемой весовой функции фильтра (рис.4в), причём в данном случае выбор параметров b и c не зависит от выбора параметров r1 и r2. Так же, как и в случае бинарного полосового фильтра, выбираем
r1 >> ℓ (ℓ/r1 »
10) (33)
где ℓ - ширина линий на изображении.
Из соотношений, аналогичных (29)-(32), находим оптимальные значения параметров k и q (k=b/c, q=r2/r1)
Частотная характеристика пространственного фильтра определится как Фурье-спектр оптимизированной весовой функции
Hопт(w
х,w
у) = J[hопт(x
,h
)] (34)
Однако в данном случае частотная характеристика может оказаться знакопеременной и, следовательно, реализация желаемого фильтра в виде бинарной маски становится невозможной.
Единственным средством регистрации комплексного спектра является голограмма Фурье.
Представим оптимизированную весовую функцию hопт(x
,h
) в видe разности
hопт(r) = h'опт-h''опт (35)
где
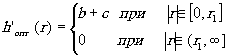 (36)
(36)
и
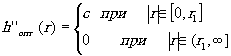 (37)
(37)
Тогда выражение (34) приобретает вид
Нопт = J[h'опт-h"опт] (38)
- 291 -
Рассмотрим схему изготовления фильтра с частичной характеристикой Нопт (рис.10).
Вначале (рис.10а) в предметной плоскости Р1 устанавливается диафрагма с апертурой r1 и освещается плоскопараллельным монохроматическим лучом, интенсивность которого равняется b+с. При введении в схему опорного луча фотопластина зарегистрирует в частотной плоскости распределение
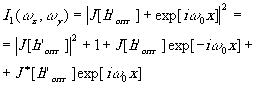 (39)
(39)
Затем (рис.10б) производится вторичное экспонирование фотопластины, но при этом в плоскости Р1 устанавливается диафрагма с апертурой r2, интенсивность сигнального луча изменяется до значения с, а в опорный луч вводится фазовая пластина, сдвигающая фазу луча на p
. При вторичном экспонировании фотопластина зарегистрирует распределение:
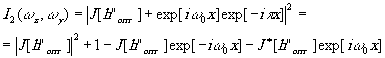 (40)
(40)
Суммарная голограмма:
- 292 -
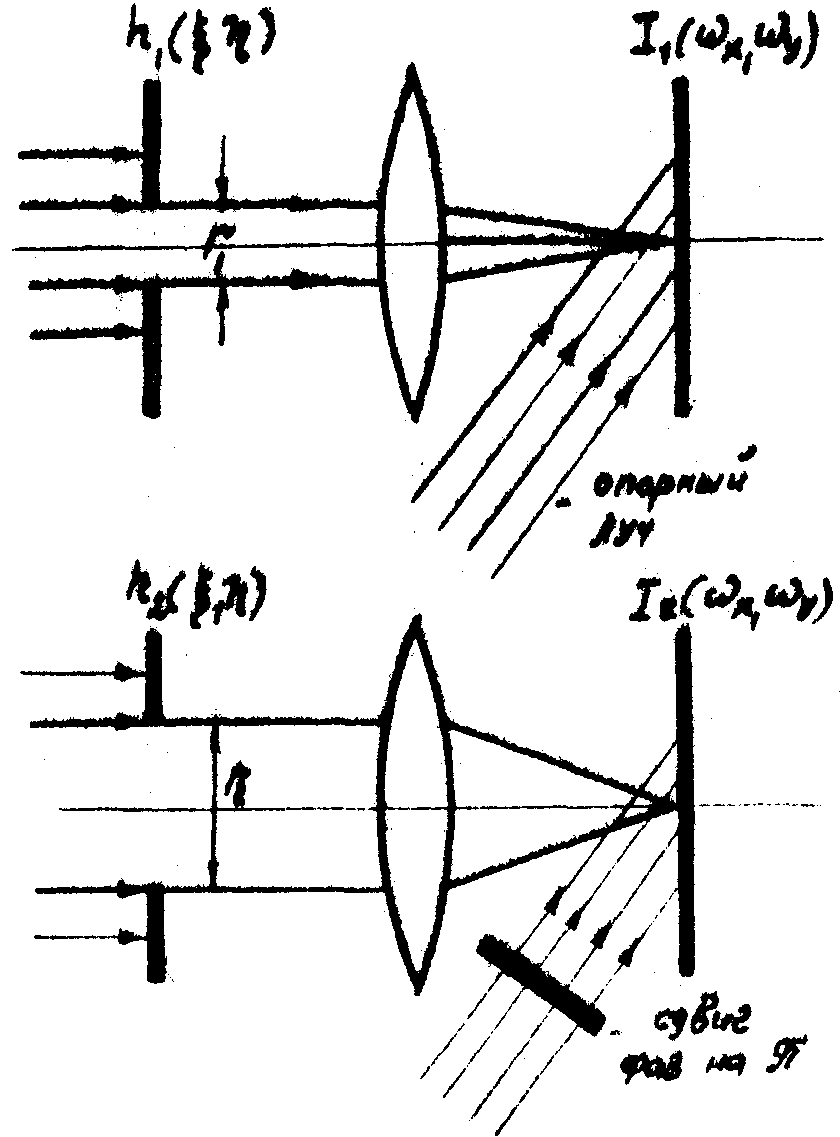
Рис.10.
- 295 -
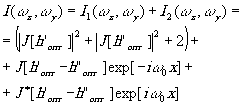 (41)
(41)
Мы видим, что третий член выражения (41) и представляет собой требуемую частотную характеристику фильтра.
Аналогичным образом могут быть построены и остальные из рассмотренных фильтров.
Большим достоинством голограммных фильтров, предназначенных для анализа структуры изображения, является то, что они все могут быть записаны на одну голограмму при равных углах падения опорного луча. Это позволяет анализировать изображение параллельно по многим каналам без предварительного его размножения.
- 294 -
Л и т е р а т у р а
1. И.И.Цуккерман. О вводе информации в мозг и вычислительную машину. Информация и кибернетика, М., 1967.
2. Narasimhan R. Labeling schemata and syntactic description of pictures. Information and control, 7, 2 (1964).
3. R.Narasimhan. Syntax directed interpretation of classes of pictures. Communications of the ACM, 9, 3 (1966).
4. В.П.Романов. Метод структурной лингвистики в задаче распознавания образов. Труды III Всесоюзной конференции по информационно-поисковым системам и автоматизированной обработке, научно-технической информации, Москва, ВИНИТИ, ч.3, стр.85, 173, 1967.
5. А.П.Петров, Г.М.Зенкин. Анализ изображения, применяемый в модели, обучающейся узнаванию зрительных образов. Труды III Всесоюзной конференции по информационно-поисковым системам и автоматизированной обработке научно-технической информации. Москва, ВИНИТИ, ч.3, стр.187-195, 1967.
6. Г.М.Зенкин, А.П.Петров. Система анализа изображений и узнавание объектов на сложном фоне. Биофизика, 12, вып.3, 1967.
7. В.Д.Глезер. Механизмы опознания зрительных образов, М., 1967.
8. Дж.Леттвин и др. Что сообщает глаз лягушки мозгу. Сб. Электроника и кибернетика в биологии и медицине, ИЛ, 1963.
9. M.S.Dobrin. Optical processing in the earth sciences. IEEE Spectrum sept., 1968.
10. Л.М.Сороко. Конспект лекций по голографии, издание МФТИ, 1967.
11. Sadac Fujimura. Japanese Journal Applied Physics, 7, 1 (1968).

