Теорема Ван Циттерта-Цернике. Когерентность при освещении протяженным квазимонохроматическим источником
Две точки Р1 и Р2 (рис.6), находящиеся в плоскости yОz, освещены источником S. Вычислим степень когерентности колебаний, приходящих в эти точки.
Пусть источник S является элементом плоскости, параллельной yOz, и его размеры малы по сравнению с расстоянием СО. Точка М - некоторая точка источника S. Углы, образованные направлением СО с МР2 и МР1, малы.
Поместим точку Р2 в начало координат 0, точку P1 будем считать переменной. Функция взаимной когерентности колебаний в точках Р1 и Р2 будет
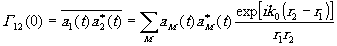 (6.1)
(6.1)
Волна, пришедшая в точку наблюдения, есть сумма волн от различных точек источника. Но так как излучение от разных точек (т.е. от разных атомов) некогерентно, то в первоначальной двойной
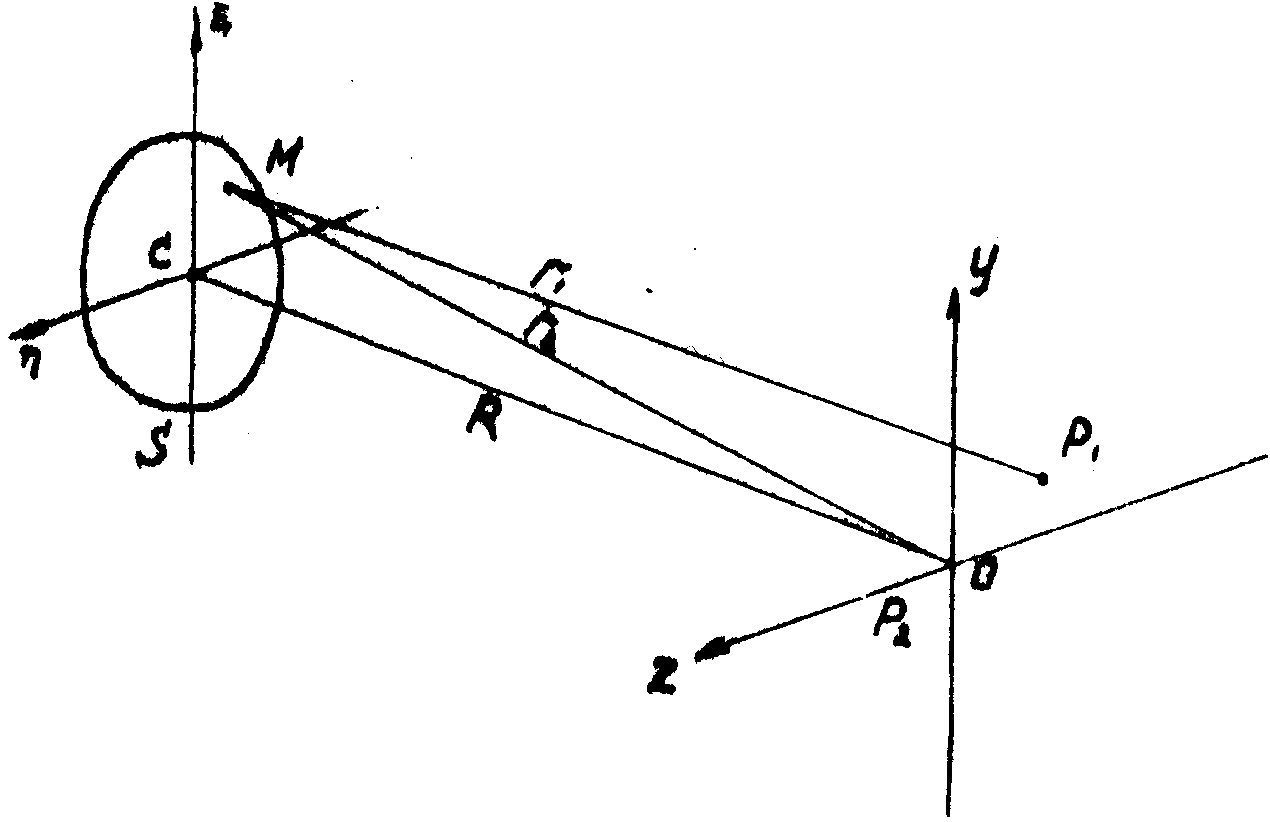
Рис.6. К определению степени когерентности.
сумм останутся только члены, связанные с временной когерентностью излучения из данного атома.
В формуле (6.1) аргументы в аМ и аМ* должны отличаться на q
. Так как изменение этих функций от t происходит значительно медленнее, чем изменяется экспоненциальный множитель, то различием в аргументах км пренебрегаем. Это совпадает с условием, что (r2-r1)<<ℓ длина когерентности.
Замечая, что
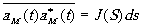 (6.2)
(6.2)
есть энергия, излученная элементом источника dS, и заменяя в(6.1) сумму интегралом, получим
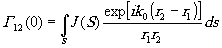 (6.3)
(6.3)
Отсюда для степени комплексной когерентности получим
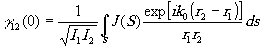 (6.4)
(6.4)
где
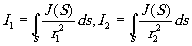 (6.5)
(6.5)
Величины I1 и I2 представляют собой интенсивность в точках Р1 и Р2. Поместим теперь в плоскости источника экран с отверстием той же формы и величины, что и источник. Это отверстие вырезает участок поверхности сферической волны с центром в Р2. Из-за дифракции на отверстии в плоскости yОz появится некое распределение амплитуды (Р2- центр дифракционной картины). Формула (6.4) показывает, что степень комплексной когерентности в точках Р1 и Р2 выражается подобно амплитуде в точке Р1 в указанной дифракционной картине. Это и есть теорема Вам Циттерта-Цернике.
Формуле (6.4) можно придать другой вид, воли ввести прямоугольные координаты точки М в плоскости источника (x
,h
) соответствующие (y,z) в плоскости наблюдения. Обозначая расстояние СО через R и учитывая, что расстояния точки Р1 от Р2 и М от С значительно меньше R, без труда найдём
 (6.6)
(6.6)
Обозначая
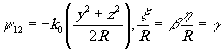 (6.7)
(6.7)
мы можем записать степень комплексной когерентности в виде
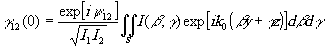 (6.8)
(6.8)
Так как
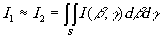
то окончательно получим
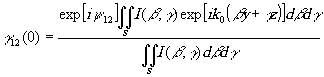 (6.9)
(6.9)
Степень комплексной когерентности выражается через нормированное преобразование Фурье от распределения энергии I(b
,g
), полученной источником.

