Степень когерентности при освещении однородным круговым источником
В качестве примера на применение теоремы Ван Циттерта-Цернике вычислим степень когерентности поля в двух точках, освещённых круговым однородным некогерентным источником. Пусть источник S представляет собой однородно светящийся круг радиусом r
с центром в С.
Полагая в формуле (6.9) I(b
,g
)=const, получим
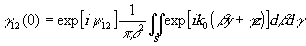 (7.1)
(7.1)
Перейдём в плоскости источника к полярным координатам. Заменим
также выражение
b y+g
z на
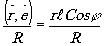 , где
, где
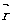 и
и 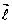 соответственно, радиусы-векторы точек М и Р1.
Для интеграла в (7.1)
теперь имеем
соответственно, радиусы-векторы точек М и Р1.
Для интеграла в (7.1)
теперь имеем
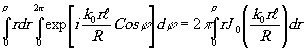 (7.2)
(7.2)
так как из теории бесселевых функций известно, что
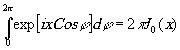
Учитывая также, что
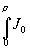 (ær)rdr
= J1(ær )r
2/ær , æ =
(ær)rdr
= J1(ær )r
2/ær , æ = 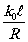
окончательно получим
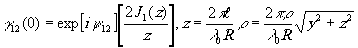 (7.3)
(7.3)
Модуль величины g
12(0) изображен на рис.7.
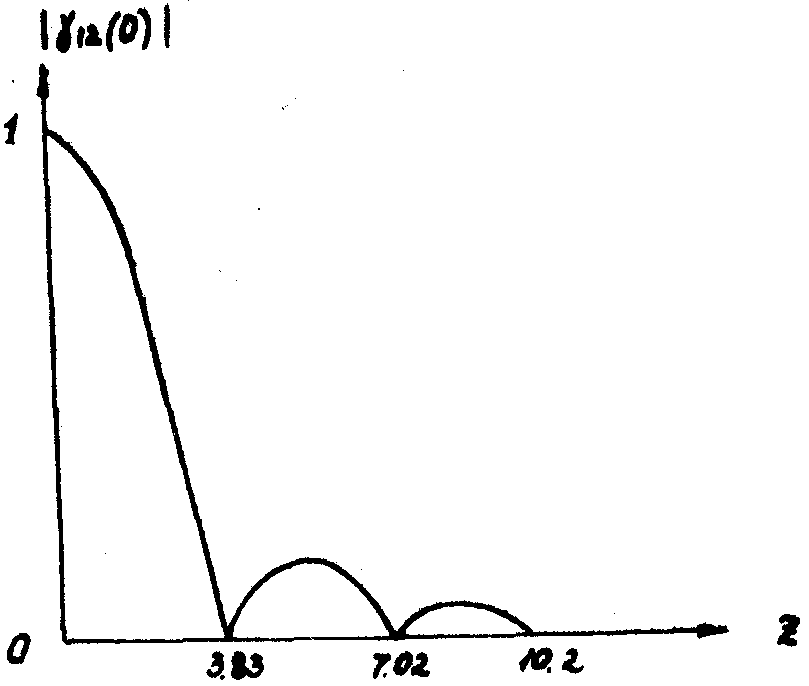
Рис.7. Зависимость модуля g
12(0) от Z.
При z=0, т.е. если точки Р1 и Р2 совпадают, степень частичной когерентности максимальна и равна единице.
Если z возрастает, то |
g
12(0)|
уменьшается и при z=3,83 становится равной нулю. Следовательно, колебания в точках Р1 и Р2 полностью некогерентны, если
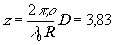 (7.4)
(7.4)
т.е.
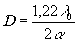 (7.5)
(7.5)
где a
=r
/R - угол, под которым из точки Р2 виден радиус источника, D- расстояние между точками Р1 и Р2.
Любопытно, что с увеличением D за значение, указанное в формуле (7.5), степень частичной когерентности начнёт снова возрастать. Она будет максимальна в точках, где z=5,14; 8,42; 11,6; и снова обратится в нуль при z=7,02; 10,2;... Во вторичном и последующих максимумах степень комплексной когерентности соответственно будет равна 0,132; 0,065; 0,04;... Разумеется, эти значения столь малы, что практически поля можно считать некогерентными. Если считать допустимой степень частичной когерентности, равную 0,88, то из формулы (7.3) следует, что расстояние D между точками Р1 и Р2 не должно превосходить 0,16l
0/a
. Это согласуется с наблюдением Верде, о котором мы писали во введении. Если расстояние между двумя точками в экране, освещённом Солнцем, будет весьма мало, то выходящие из них вторичные волны нельзя считать некогерентными. Юнговские интерференционные картины в этом случае уже не будут независимы, и в результате их наложения появятся дополнительные интерференционные детали.

