Последовательные цуги волн, излученные одним атомом
Вернёмся к формуле (2.1) для колебания F(t), вызванного прохождением одного цуга волн.
Вводя среднюю частоту u
0, вокруг которой распределяемся частота u
, получаем
F(t) = exp(i2p u
0t)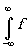
(u
)exp[i2p (u
-u 0)t]du
(3.1)
Пусть
d(t) = 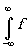(u
)exp[i2p (u
-u 0)t]du
(3.2)
где d(t) - в общем случае комплексное число вида A(t)ℓiф(t). Тогда получим
F(t) = d(t)ℓi2p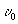 
t (3.3)
Колебание, описываемое (3.3), можно считать монохроматическим колебанием с частотой, равной средней частоте u
0, и с переменной амплитудой d(t). d(t) - это мгновенное значение комплексной амплитуды колебания.
Предположим, что ¦
(u
), т.е. спектр F(t), отличен от нуля только при значениях u
, близких к u
0. Интеграл представляет суперпозицию гармонических составляющих с частотами (u
-u
0), т.е. низкочастотных составляющих. Иными словами, если интервал D
u
, внутри которого ¦
(u
) отлично от нуля, мал по сравнению со средней частотой u
0, то exp[i2p
(u
-u
0)t] будет изменяться во времени медленнее, чем exp[i2p
u
0t]. Излучённый свет окажется квазимонохроматическим. В выражении (3.3) изменения d(t) во времени значительно медленнее изменений колебательного члена exp(i2p
u
0t).
За время наблюдения атом излучает большое число цугов, не связанных по фазе. Предположим, что атом излучает цуги волн F1(t), F2(t),... в случайно распределённые моменты времени t1, t2,...
Цуг F1(t) излучённый в момент времени t1, будет представлен
выражением F1(t-t1) в момент времени t. То же относится и к другим дугам, и суммарное колебание в момент времени t можно записать в виде
V(t) = F1(t-t1)+F2(t-t2)+... (3.4)
Эти цуги могут иметь любую форму и продолжительность t
1, t
2... Фазы каждого цуга неодинаковы, и между фазами различных цугов нет никакой связи. В соответствии с (1.3) получим
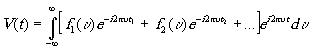(3.5)
Выделяя среднюю частоту u
0, получим
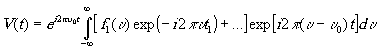(3.6)
Положим
d(t) =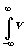 
(u
)exp[i2p (u
-u 0)t]du
(3.7)
v(u
) = ¦
1(u
)exp(-i2p
u
t1)+... (3.8)
Тогда
V(t) = d(t)exp(i2p
u
0t) (3.9)
Это выражение идентично выражению (3.3), но оно описывает явление для последовательности большого числа цугов волн.
Амплитуда d(t) представляет собой теперь комплексную амплитуду результирующей большого числа последовательных цугов. Если все члены, входящие в d(t), отличаются от нуля только для значений u
, близких к u
0, то d(t) изменяется медленно по сравнению с изменением колебательного члена exp(i2p
u
0t) в выражении (3.8), так же,
как и в случае одного цуга. Но, разумеется, изменения d(t) крайне быстры по сравнению с нашими возможностями наблюдения.
Приемное устройство может отметить лишь усредненный эффект. Если 2Т - время наблюдения, то для среднего значения d(t) получим
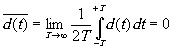
так как в комплексной плоскости для каждой величины d(t) всегда можно найти величину с противоположным знаком. Приёмное устройство - глаз или фотоэлектрический регистратор - чувствительно лишь к среднему |d(t)|2 квадрату модуля величины d(t). Интенсивность света характеризуется величиной
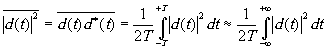(3.10)
