Media-security

Корреляции при интерференционных явлениях. Степень частичной когерентности

Рассмотрим опыт Юнга (рис.4): протяженный источник S освещает экран E₁ с двумя очень маленькими отверстиями Т₁ и Т₂. Изучается распределение света на втором экране E₂. Световые волны, излучённые источником, можно представить выражением

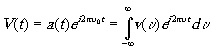(4.1)

Предположим, что V(t)- это волна, приведшая от источника в некую точку плоскости E₁. Пусть q - время, за которое свет прошёл от Т₁ до точки Р в плоскости наблюдения E₂. Колебание в Р в момент времени t совпадает с колебанием Т₁ в момент времени t-q ₁. Оно описывается выражением V₁(t-q ₁). To же относится и

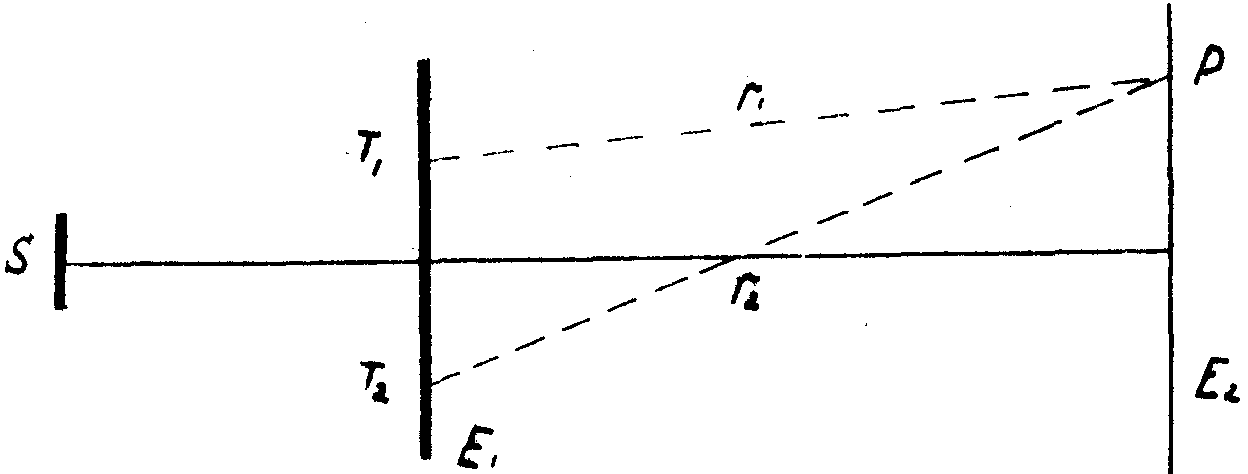
Рис. 4. Схема интерферометра Юнга.

к колебанию, создаваемому Т₂ в Р, которому соответствует V₂(t-q ₂).

"Мгновенное" колебание в Р описывается выражением

V(t) = V₁(t-q ₁)+V₂(t-q ₂) (4.2)

Приёмное устройство чувствительно к среднему значению величины ï V₁+V_2ï², взятому за время наблюдения. В соответствии с (3.10) интенсивность в Р запишется в виде

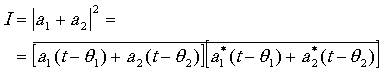(4. 3)

Раскрывая скобки, получим

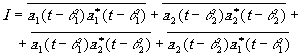(4.4)

Излучение источников Т₁ и Т₂ в среднем неизменно. Это означает, что мы можем изменить начало отсчёта времени, т.е.

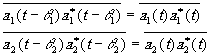(4.5)

Положим

q = q ₂-q ₁

Тогда имеем

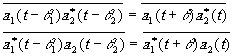(4.6)

Но а₁ и а₂ суть комплексные величины, и мы имеем

a₁(t+q )a₂^*(t)+a₁^*(t+q )a₂(t)=2Re[a₁(t+q )a₂^*(t)] (4.7)

Отсюда интенсивность равна

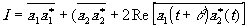(4.8)

Положим

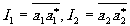(4.9)

Это интенсивности, создаваемые в Р освещёнными отверстиями Т₁ и T₂, действующими по отдельности. Последний член в правой части (4.8) представляет собой корреляционную функцию величин а₁ и а₂. Этот член характеризует взаимосвязь, т.е. когерентность колебаний, пришедших от Т₁ и Т₂ в точку наблюдения Р.

Функцию 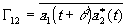называют взаимной когерентностью колебаний, излучённых Т₁ и Т₂ и пришедших в точку Р . Нормируя Г₁₂(q ), получаем

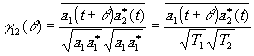(4.10)

Величину g ₁₂(q ) называют степенью комплексной когерентности колебаний, излученных Т₁ и Т₂ и пришедших в Р. Соотношение (4.8) можно теперь записать в виде

I = I₁+I₂+2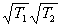Re[g ₁₂(q )] (4.11)

Запишем комплексные числа Г₁₂(q ) и g ₁₂(q ) в виде

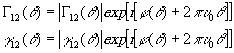(4.12)

Величина

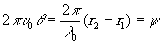
есть разность фаз s Р обоих колебаний. Теперь для I получим

I = I₁+I₂+2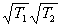|g ₁₂(q )|Cos[j (q )+y ] (4.13)

Очевидно, что с ростом q модуль степени комплексной когерентности может только убывать, так как с увеличением расстояния между точками корреляция колебаний в них убывает. Это означает, что

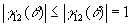(4.14)

Формально соотношение (4.14) легко получить из неравенства Буняковского-Щварца. Для любых двух случайных величин х и у будет

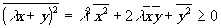(4.15)

Поскольку соотношение (4.15) имеет место при любом l , квадратное уравнени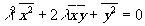е не должно иметь различных вещественных корней, т.е.

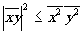
Это и есть неравенство Буняковского-Шварца для нашего случая. Применим его к случайным величинам а₂^*(t) и а₁(t+q ). Имеем

| а₂^*(t)а₁(t+q )| ² £ | а₂^*(t)| ^2×
|а₁(t+q )| ² = I_1×I₂ (4.l6)

Извлекая квадратный корень из обеих сторон равенства, найдём формулу (4.14).

Из (4.14) вытекает, что наибольшая интенсивность в случае, если речь идёт об интерференционной картине с яркой центральной полосой (или наименьшая, если речь идёт об интерференции с тёмной центральной полосой), всегда бывает в центре. В частности, такая картина, какая показана на рис.5, невозможна.

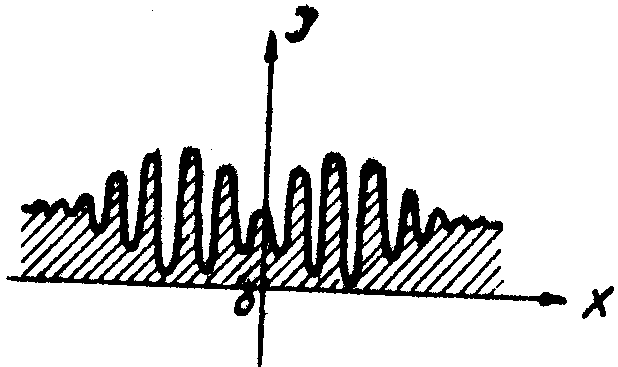
Рис.5.