Контраст полос в квазимонохроматическом свете
В теории преобразования Фурье доказывается, что между двумя Функциями F1(t) и F2(t) и их Фурье-спектрами ¦
1(u
) и ¦
1(u
) (см.(2.1)) имеет место следующее соотношение
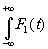 F2*(t)dt
=
F2*(t)dt
= 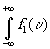 ¦
2*(u )du
(5.1)
¦
2*(u )du
(5.1)
Эта формула называется теоремой Парсеваля. Из этой теоремы и, учитывая (5.10), легко получим, что
a1(t+q )a2*(t)
= 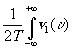 v2*(u
)exp[i2p u q
]du (5.2)
v2*(u
)exp[i2p u q
]du (5.2)
или
| Г12(q
)| ехр[ij
(q )]=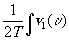 v2*(u
)exp[i2p (u
-u 0)q
]du (5.3)
v2*(u
)exp[i2p (u
-u 0)q
]du (5.3)
В квазимонохроматическом свете u
»
u
0 и интеграл (5.3) содержит лишь члены с низкими частотами. Это означает, что величина |
Г12(q
)|
или |
g
12(q
)|
и j
(q
) как функции q
меняются значительно медленнее, чем exp(i2p
u
0q
).
Следовательно, когда точка Р перемещается в плоскости Е2 (см.рис.4), можно считать, что |
Г12(q
)|
остаётся практически постоянным. Кроме того, если отверстия Т1 и Т2 достаточно малы, то I1 и I2 также остаются постоянными в плоскости Е2. В формуле (4.13) для интенсивности все члены постоянны, кроме y
. Светлые полосы с Iмакс будут наблюдаться там, где
j (q
)+y = j (q
)+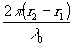 = 2mp
(5.4)
= 2mp
(5.4)
при m= 0,±
1..., а тёмные полосы Iмин там, где
j (q
)+y = j (q
)+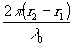 = (2m+1)p
(5.5)
= (2m+1)p
(5.5)
Имеем
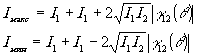 (5.6)
(5.6)
Отсюда контраст между полосами запишется в виде
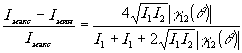 (5.7)
(5.7)
и, если I1=I2, то
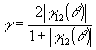 (5.8)
(5.8)
Из формул (5.4) и (5.5) видно, что светлые и тёмные полосы в квазимонохроматическом свете, находятся там же, где и в полностью монохроматическом свете, но фаза волны, пришедшей из Т2, запаздывает на j
(q
) по сравнению с фазой волны из Т1. Величина j
(q
), таким образом, имеет смысл разности фаз пришедших волн, а величина j
(q
) означает, следовательно, разность фаз волн, излучённых Т1 и Т2. Если степень монохроматичности излучения велика, то длина когерентности ℓ будет значительно больше разности хода d
:
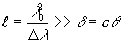 (5.9)
(5.9)
Это означает, что
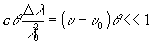 (5.9)
(5.9)
т.е. что интеграл справа в формуле (5.3) имеет примерно то же значение, что и при q
=0. Следовательно,
|
Г12(q
)|
»
|
Г12(0)|
, |
g
12(q
)|
»
|
g
12(0)|
, j
(q
) =j
(0)
Г12(0) = а1(t)a2*(t), g
12(0) = |
g
12(0)|
eij
(0) (5.11)
Интенсивность в точке Р будет
I = I1+I2+2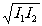 |
g 12(0)|
Cos(j (0)+y
) (5.12)
|
g 12(0)|
Cos(j (0)+y
) (5.12)
а контраст полос (I1=I2) теперь равен
 (5.13)
(5.13)

