Временная и пространственная когерентность
Различают два вида когерентности: 1) временную или продольную и 2) пространственную или поперечную. Первая связана с нарушением строгой гармоничности волн во времени, например, с конечностью длины цуга волн, испускаемых отдельными атомами. Вторая - с фазовыми сдвигами при сложении вторичных волн, испущенных из разных точек плоской волны.
Рассмотрим схему интерферометра Майкельсона (рис.1). Пусть S точечный источник, излучающий монохроматический свет, находится в фокусе объектива О. Интерферометр будет освещён параллельным пучком. Пучок, отражённый полупрозрачным зеркалом G, нормален к зеркалу М1, а пучок, проходящий сквозь G, нормален к зеркалу M2. Наклоним слегка М2 таким образом, чтобы M2' (изображение М2 в полупрозрачном зеркале G) образовало бы очень малый угол с М1. Все происходит так, как если бы мы наблюдали полосы равной толщины в слое воздуха переменной толщины, заключённого между М1 и М2'.
В точке В, где толщина слоя равна ℓ, разность хода лучей равна d
=2ℓ. Если l
- длина волны света, излучённого S, то для амплитуды суммарного колебания SA имеем
А2 = а12+а22+2а1а2Cosj
.
Здесь а1
и а2
- амплитуды слагаемых колебаний, j - разность
фаз колебаний, соответствующая разности хода d
: j = 2ℓ
2ℓ
Полагая а1 = а2 для интенсивности света в B, найдём (с точностью до постоянного множителя)
J = 2a2(1+Cosj
) = 4a2Cos2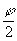 = 4a2Cos2(2p ℓ/l
) (1.1)
= 4a2Cos2(2p ℓ/l
) (1.1)
Так как толщина слоя ℓ переменна, то мы будем наблюдать ряд интерференционных полос, параллельных ребру двугранного угла между плоскостями М1 и M2'.
Пусть I1 - интенсивность светлых полос, а I2 – интенсивность тёмных. Обозначим контраст полос через g
и зададим его следующим образом:
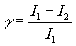 (1.2)
(1.2)
Этот параметр определяет видимость интерференционной картины.
Соотношение (1.1) показывает, что I2 равна нулю каждый раз, когда толщина ℓ равна нечётному числу l
/4. Тогда тёмные полосы становятся чёрными и g
=1; в этом случае контраст максимален. В схеме, изображённой на рис.1, контраст равен единице при любом расстоянии между М1 и М2'. Однако опыт показывает, что это никогда не наблюдается по следующим двум причинам, имеющим принципиальный характер: излучаемый свет не вполне монохроматичен, источник всегда имеет конечную (а не нулевую) протяжённость.
Электромагнитные волны не бесконечны. Они излучаются в виде цугов конечной длины. Поскольку цуг имеет конечную длину, то как мы увидим, атом излучает не одну какую-нибудь частоту, а целый спектр частот, ширина которого тем больше, чем меньше длина дуга. Это влечёт за собой уменьшение контраста между полосами, что непосредственно видно из формулы (1.1) (каждой длине волны соответствует определённая интенсивность света, наблюдаемого в точке В (рис.1). Если для длины волны l
мы наблюдаем нулевой минимум в B, то для других длин волн картина оказывается уже иной и контраст между полосами уменьшится. Видимость полос связана с хроматизмом источника. В этом случае говорят о явлении временной или хроматической когерентности.
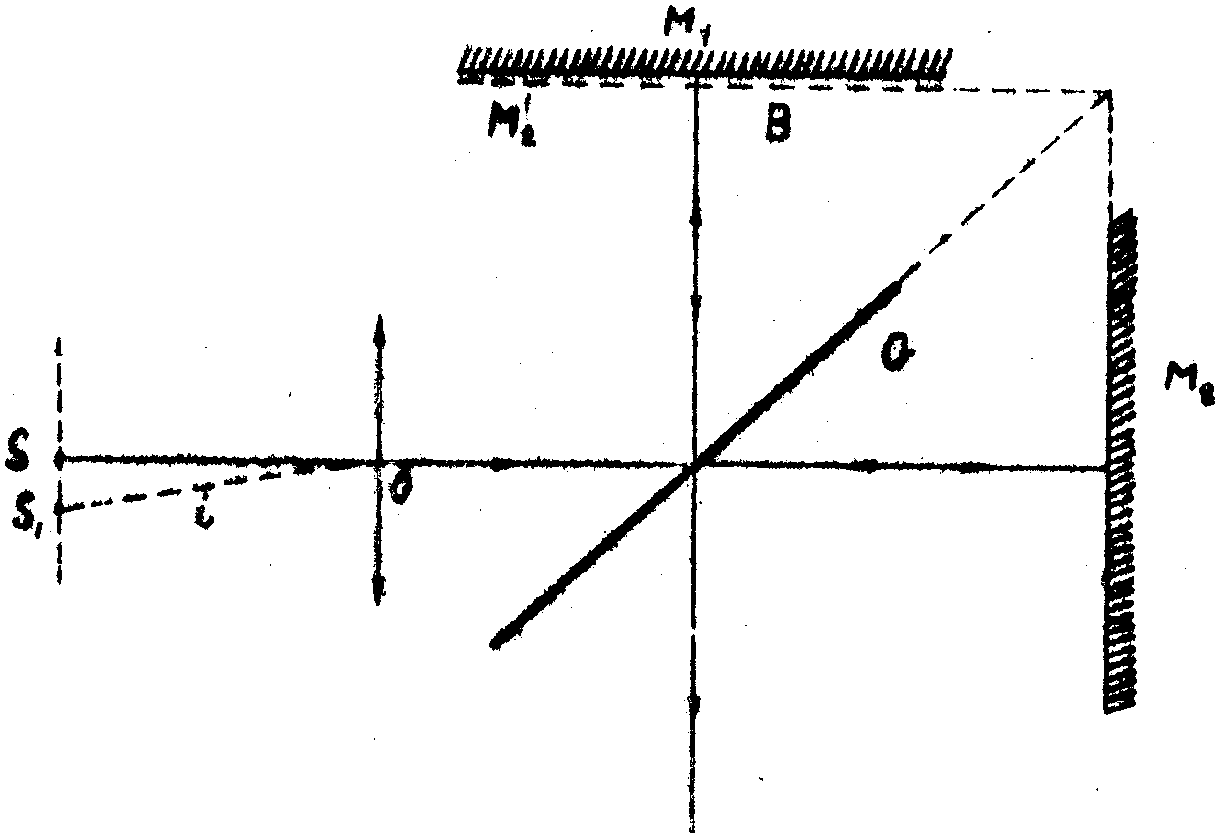
Рис.1. Схема интерферометра Майкельсона.
Это явление можно изучать также, если непосредственно вводить длину цугов волн. Будем постепенно удалять одно из зеркал интерферометра. Опыт показывает, что контраст полос начинает ухудшаться. Это вызвано конечной длиной волновых цугов, испускаемых атомами источника. При попадании в интерферометр каждый цуг, например, цуг А, разделяется полупрозрачным зеркалом G на два (рисунок 2). Установим такую разность хода между путями 1 и 2, чтобы она была больше длины цугов волн. Если достаточно далеко удалять зеркало М2, то в момент, когда цуг А1, шедший путём 1, придет в Р, другой цуг будет находиться лишь в А2'. Эти два цуга не встретятся и не смогут интерферировать. Цуги, налагающиеся друг на друга в точке Р, испущены в моменты t и t+q
.
Рассмотрим сначала случай, изображённый на рис.2, где q
гораздо больше длительности цуга t
.
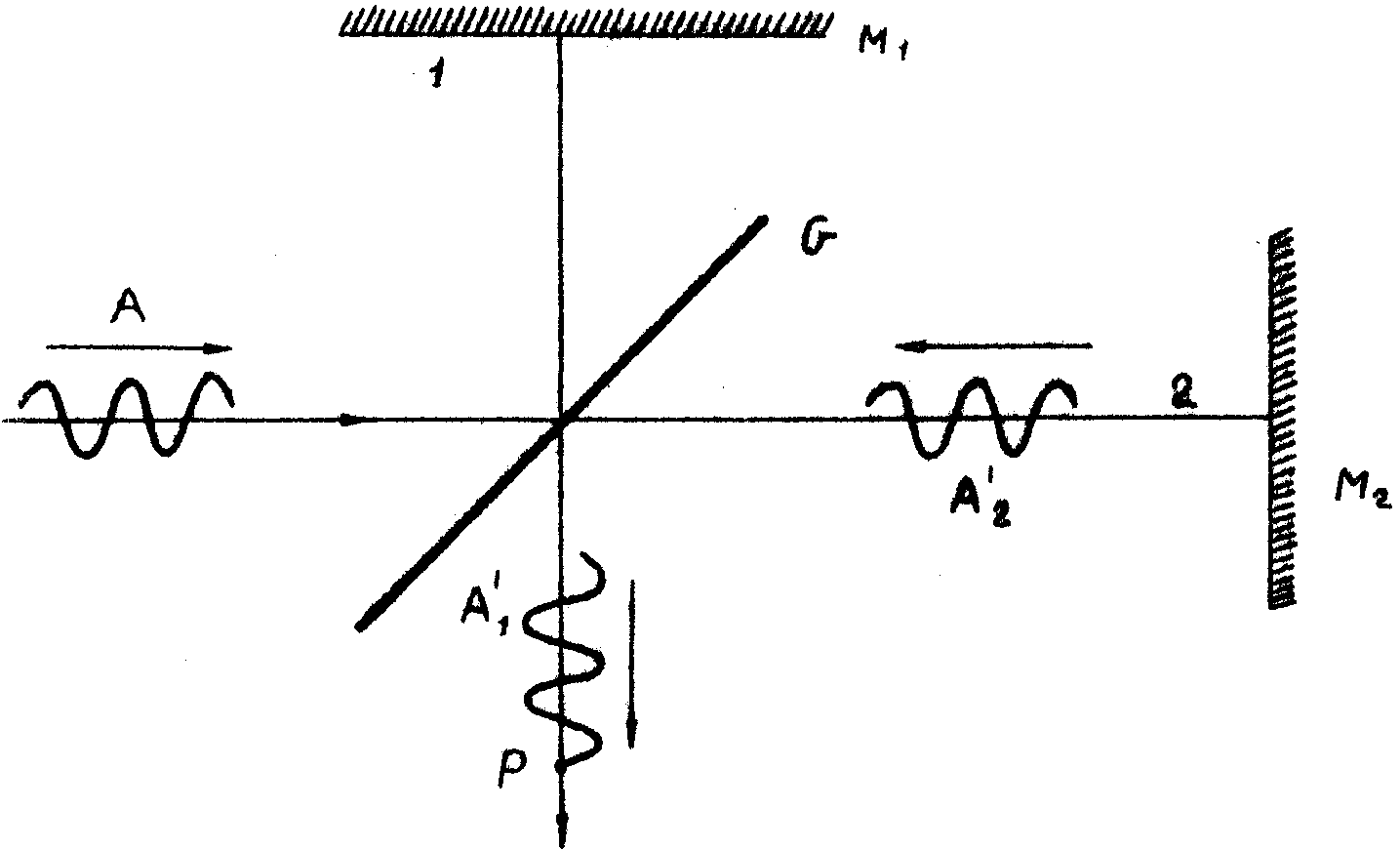
Рис.2. Взаимодействие цугов волн в интерферометре Майкельсона.
За время наблюдения проходит множество цугов, причём моменты их прохождения распределены случайно. Если учитывать, что разность фаз между цугами принимает всевозможные значения, то ясно, что интерференция наблюдаться не будет.
Картина изменится, если разность хода уменьшится, так как при этом промежуток времени q
также уменьшится. При q
порядка t
оба цуга, происходящие из одного начального, частично перекрываются. Между этими цугами существует "корреляция": и она сохраняется для всех цугов, приходящих в Р. Появляются интерференционные полосы с большим или меньшим контрастом и возникает частичная когерентность пучков 1 и 2. Если разность хода настолько мала, что q
значительно меньше t
, то полосы оказываются очень контрастными.
Всё вышеизложенное относилось к временной когерентности. Явление пространственной когерентности связано с конечными размерами источника. При увеличении размеров источника контраст между полосами уменьшается. Обратимся снова к рис.1. Для точки S1, видной из точки О под углом i, разность хода в B равна d
=2ℓCosi. Для разных точек протяжённого источника как разность хода d
, так и разность фаз j
, неодинаковы. Поскольку изменяется разность фаз j
, то и интенсивность I, создаваемая в B точкой S1 протяжённого источника, также будет изменяться в зависимости от положения этой точки. Если для какой-то определённой точки источника S получается нулевой минимум в B, то для других точек источника это будет не так. Различия в разности фаз j
для разных точек источника приведут к уменьшению контраста между полосами.
Если изменения j
достаточно малы, то они могут повлечь за собой лишь пренебрежимо малые изменения интенсивности, - в этом случае имеет место пространственная когерентность. Большие изменения j
могут привести к столь большим изменениям I, что контраст упадёт практически до нуля. Тогда полосы становятся неразличимыми - имеет место пространственная некогерентность. Рассмотрение промежуточных случаев позволяет ввести определение различных степеней частичной когерентности в случае пространственной когерентности.

