ФИЗИЧЕСКИЕ ОСНОВЫ ГОЛОГРАФИИ

С.М.Рытов

Для нас чрезвычайно привычно мнимое оптическое изображение, появляющееся при любом освещении, в натуральном масштабе, по настоящему объёмное, цветное и даже движущееся. Это изображение в плоском зеркале. У него только два недостатка: оно показывает нам мир перевернутым слева направо и появляется, как и все изображения, даваемые линзами и зеркалами, только при наличии самого объекта. Нас не могут поэтому поразить высокие качества мнимого изображения, взятые сами по себе, но нас действительно потрясло бы появление такого изображения в отсутствие объекта.

Этот момент был учтён устроителями Французской промышленной выставки в Политехническом музее, где демонстрировалась большая голограмма, дававшая изображение статуи - бюста Лафонтена. Голограмма была вставлена в переднюю стенку большого деревянного ящика и освещалась сзади зелёной линией ртутной лампы. Зритель видел позади этой немного мутной плёнки весьма натуральную статую и, так как перед голограммой объект отсутствовал, вполне мог посчитать, что позади неё поставлен этот бюст. Именно поэтому в боковой стенке ящика были сделано большое отверстие, позволявшее убедиться, что за голограммой пусто...

Если не говорить о живописи, то изображение объекта, наблюдаемое уже без его присутствия, появилось в прошлом веке, точнее 130 лет тому назад. Это фотографическое изображение, фиксирующее проекцию объемного оригинала на плоскость.

Сегодня нас здесь уже ничто не поражает. Такие фотопроекции уже давно делаются высококачественно цветными, а при помощи некоторых ухищрения, основанных, в сущности, на оптических обманах, их делают и движущимися, и субъективно объёмными или стереоскопическими.

Немногим более 20 лет назад Габор, занимаясь в Лондонском имперском колледже вопросами об устранении аберраций электронного микроскопа, пришёл к идеям, из которых развилась голография. Голографические методы позволяют получать мнимое и действительное изображение объекта, изображения цветные, а главное - по-настоящему объёмные. Очень жёсткие по началу ограничении условий, необходимых для получения и наблюдения таких изображений, шаг за шагом ослабляются и обходятся. В воздухе уже носится, если не идея, то предчувствия голографических кинематографии и телевидения, с которыми уже давно и запросто оперируют авторы фантастических романов.

Мне надлежит говорить о физических принципах голографии, но если вдуматься, то это не простая тема, так как неясно, существуют ли вообще какие-то особые физические принципы голографии.

Спросим себя сначала, существуют ли такие принципы у обычной фотографии?

Если понятие физического принципа толковать очень широко, включая в него не только законы оптики, но и физические основы действия фотоэмульсий, принципы образования скрытого изображения и т.п., то, конечно, существуют. Но с точки зрения теоретической физики - физики принципов - это завело бы нас довольно далеко. Если же ограничить область принципов общими законами оптики, то можно сказать, что никаких особых физических принципов у обычной фотографии нет и что родилась она в результате технического прогресса, в результате открытия хорошего фотохимического способа фиксации освещённости, даваемой линзами и зеркалами по давно а хорошо известным законам.

Точно так не обстоит дело и с голографией - безлинзовым способом создания объемных изображений.

Физические принципы голографии - это общие принципы учения о волновых процессах, учения об интерференции и дифракции волн. Они берут своё начало от Гюйгенса, а затем, ещё в прошлом веке, получают блестящее развитие у Френкеля и математическое завершение у Кирхгофа. Чего же не хватало, чтобы уже тогда делать голограммы?

Если говорить о действительно физических принципах, то в прошлом веке не хватало принципа индуцированного излучения, а после того, как Эйнштейн постулировал существование такого излучения, ещё долгое время, даже Габору, не хватало реализации этого принципа в виде оптического квантового генератора. Лишь после того, как в 1960 году появился лазер - высококогерентный источник света, завершилось создание необходимых предпосылок, и вскоре развитие голографии быстро двинулось вперед. Таким образом, и здесь поворотным пунктом оказался технический прогресс - изобретение лазера.

Несомненно, без лазера, без высокой пространственно-временной когерентности голография еще очень долго не возникла бы. Правда, сегодня требование высокой когерентности уже ощущается как недостаток и для практических нужд стараются ослабить жёсткость этого условия.

Но если дело было за лазером, то естественно возникает вопрос, вчем же заключается заслуга Габора? Чтобы лучше ответить на этот вопрос, надо всё же вернуться к основам учения о дифракции и интерференции. Будем говорить для простоты об идеально-монохроматических волнах.

Центральный пункт принципа Гюйгенса-Кирхгофа состоит в том, что колебания S=a× e^-ij созданные некоторой первичной волной на какой-либо достаточно обширной поверхности*, однозначно определяют всё волновое поле за этой поверхностью, если там нет других истинных источников. Элементы поверхности надо рассматривать вслед за Френкелем как виртуальные источники, колеблющиеся с амплитудой а(х,у) и фазой j (x,y) в точке (х,у), которые заданы первичной волной. После этого можно забыть первичную волну и выбросить ее источник, Интерференция элементарных сферических волн, испускаемых виртуальными источниками, восстанавливает за поверхностью первичное поле.

В сущности, основное содержание принципа шире и, говоря на математическом языке, заключается в том, что граничные условия

^к Строго говоря, речь идёт о замкнутой поверхности, в частности о плоскости, замыкаемой бесконечной полусферой.

однозначно определяют поле в остальном пространстве. Здесь не предрешается, каковы те элементарные волны, суперпозиция которых позволяет удовлетворить граничные условия. Эти элементарные линии могут быть сферическими, как у Гюйгенса, Френкеля и Кирхгофа, а могут быть и плоскими, как у Релея, или еще какими-нибудь. Ведь мы всегда можем переразложить одни волны по другим, например, сферические волны разложить по формуле Вайля на плоские и т.п. Важно только, чтобы эти волны были возможны, т.е. удовлетворяли волновому уравнению. Конечно, практически, т.е. для расчётов, целесообразно выбирать элементарные волны так, чтобы они были удобны с точки зрения формы поверхности и других геометрических условий задачи.

Итак, если мы сумеем обеспечить на поверхности - пусть для простоты на плоскости (х,у) - колебание S=a× e^-ij с точно такими распределениями a(х,у) и j (x,у), какие давала первичная волна от некоторого объекта, то позади плоскости будет распространяться именно такое волновое попе, какое исходило от объекта. Если указанное распределение амплитуды и фазы колебаний на плоскости существует и тогда, когда сам объект убран, то мы всё равно увидим его изображение так и таким, где и каким был объект.

Представим себе, например, фотоэмульсию, реагирующую на амплитуду первичной, волны почернением, а на фазу, скажем, изменением всей толщины. Экспозиция в монохроматическом свете от некоторого объекта сделает нам из такой плёнки амплитудно-фазовый экран, просветив потом этот экран немодулированной монохроматической волной, мы увидели бы, глядя через экран, изображение объекта, внешне почти ничем не отличающееся от самого объекта, и, в частности, объёмное изображение. Это было бы самое прямое осуществление принципа Гюйгенса-Кирхгофа. Беда лишь в том, что наши эмульсии фиксируют амплитуду а (точнее а²) и не фиксируют фазы j . Является ли эта трудность чисто технической или она лежит в природе вещей? Иначе говоря, потому ли нет такой эмульсии, что химики её ещё не придумали, или потому, что она в принципе не возможна?

Вдумаемся на минуту, что значит фиксировать фазу хотя бы в одной точке (х,у). Для этого необходимо иметь в данной точке стандартные "часы", т.е. другое колебание той же частоты, фаза которого послужит уровнем отсчёта. Для того же, чтобы фиксировать весь "фазовый рельеф" j (х,у), надо располагать вторым "фазовым рельефом", хотя бы j ₀=const. или j ₀=a х+b у+g . Таким образом, "чувствовать" фазу может только такая эмульсия, в которой происходит независимый от внешней волны колебательный процесс той же частоты и с каким-то известным распределением фазы, - "хронизованная" эмульсия.

В оптической диапазоне трудно, вероятно, даже невозможно создать такую внутреннюю хронизацию вещества эмульсии, хотя как раз нечто подобное легко достигается средствами радиотехники в радиодиапазоне и в акустике. Для оптики остаётся единственный путь для хронизации каждой точки плоскости, годный вообще для любых волн. Он состоит в том, чтобы послать на нашу плоскость ещё одну волну той же частоты и с известным распределением фазы j ₀(х,у). Тогда возникает интерференция обеих волн и разность фаз j (х,у)-j ₀(х,у) тотчас же "заиграет", проявляя себя в густоте и форме интерференционных полос.

Я вовсе не утверждаю, что именно этим путём шёл Габор, но в этом и заключается суть его замечательного изобретения. Он придумал, как использовать интерференцию двух достаточно монохроматических волн - одной от объекта, а другой опорной - для того, чтобы на обычной фотоплёнке, чувствительной только к интенсивности света, записать как а, так j . Амплитуда записывается при этом контрастностью интерференционных полос (пятен), а фаза j - их густотой и формой. И то, и другое фиксируется на плёнке (голограмме) обычным почернением.

Появление нового научного факта или метода всегда рождает все нарастающее количество его объяснений. Это подобно исполнению разными пианистами одного и того же музыкального произведения. Каждому кажется, что тот путь, которым он сам дошёл до понимания сути дела, - это наилучший путь и его надо поведать миру.

Отсюда, между прочим, проистекает обилие статей и книг, говорящих разными словами об одном и том же.

В настоящее время существует уже много способов объяснения того, как образуются голографические изображения: и с помощью зонных фигур, создаваемых на голограмме точками объекта (Роджерс, 1952-56), и с помощью дифракции на решётках, и даже посредством хода "лучей" через голограмму (Оффнер, 1966). Мне представляется наиболее общим и простым чисто аналитический подход, очень хорошо поданный в статье Коллера (R.I.Collier Spectrum, 3, № 7, 67, 1966).

В общем случае не обязательно, чтобы опорная волна была простой - плоской или сферической. При достаточно монохроматическом освещении будут интерферировать любые два поля, рассеянные какими-то двумя объектами 1 и 2 (рис.1).

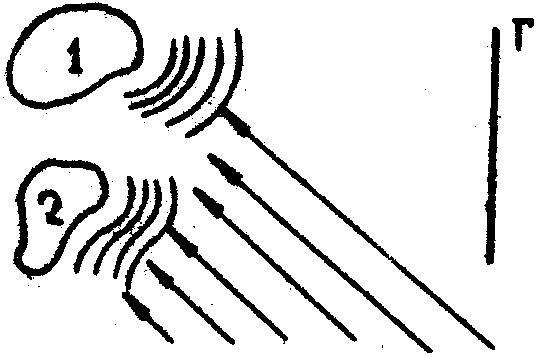
Рис.1.

Рис.1. Интерференция полей, рассеянных двумя объектами, при монохроматическом освещении.

Пусть I и есть прозрачность голограммы после проявления. Если теперь поставить голограмму точно на прежнее место и, не трогая ни объекта 1, ни источника света, убрать объект 2, то голограммой получится волна

S'=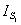=(I₁+I₂)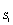+S₁²S₂^*+I₁S₂,

причём интенсивности I₁ = а₁² и I₂ = a₂² на площади голограммы меняются мало и в первой приближении могут считаться константами

Первый член в выражении для S' даёт изображение объекта 1, второй при диффузном поле S₁ не представляет интереса, а третий даёт мнимое изображение 2. Это изображение появляется там, где раньше находился сам объект 2, появляется как "дух", по словам Коллера, который пользуется здесь терминологией, возникавшей применительно к плохим дифракционным решёткам.

Ясно, что описанная процедура реконструкции волнового фронта требует точнейшего воспроизведения всей геометрии. В частности, "опорный" объект 1 не должен сдвигаться, так как иначе изображение 2 исчезнет (вместо I₁ = const будет S₁^*S_1сдвин ¹ Const ). Голография Фурье, при которой на голограмме фиксируется интерференция не самих волн, а их трансформант Фурье, даваемый линзой, снимает это условие. Объекты в этом случае плоские (слайды) и лежат в главной фокальной плоскости линзы. Как известно, голограмма инвариантна при этих условиях по отношении к параллельным сдвигам 1 или 2 в этой фокальной плоскости, но я не буду на этом задерживаться.

Частный случай, когда объект 1 - это плоское зеркало, т.е. опорная волна плоская: S₁ = a_1× e^{-ia x}, где a₁ = const. Тогда расстояние до зеркала при восстановлении изображения некритично, интенсивность I₁ = a₁² = const на всей голограмме и, кроме того, возникают ещё две особенности.

1. Если голограмма записана в толстой эмульсии (объёмная голограмма), то при восстановлении изображения должно выполняться условие Вульфа-Брегга. При плоской опорной и восстанавливающей волнах это достигается простым поворачиванием голограммы. Я лишь упоминаю об этом, но по недостатку времени больше не буду возвращаться к объёмным голограммам.

2. Начинает "работать" и второй член S'. Он теперь будет

S₁²S₂^* = a₁²e^{-2ia x}a₂(x,y)e^+i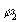(x,y)

т.е. даёт волну, сопряжённую S₂ (сходящуюся) в направлении 2a . Это действительное изображение, расположенное симметрично с мнимым по отношению к опорному пучку, и не за голограммой, где был объект 2, а перед ней.

С точки зрения теории дифракции на решетках нетрудно распознать в S₂ спектр 1-го порядка, вS₂^*e^{-2ia x} - спектр +1-го порядка, а в S₁ - нулевой или центральный максимум. Отличие от простой решетки, скажем, синусоидальной (I=I₀[1+mcos2p 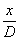]), дающей "скучную" дифракционную картину из трёх плоских волн, заключается в том, что дифракция на сложном наборе перепутанных на голограмме решёток, обладающих разными периодами, контрастами и ориентациями, даёт в спектрах ± 1-го порядков голографические изображения.

С точки зрения зонных пластинок те же три световых пучка представляют собой соответственно задний и передний фокусы зонной пластинки плюс частично пропускаемый ею без искажений опорный (восстанавливающий) пучок.

Дальше начинается вся голографическая "кухня". Здесь и разные типы голограмм (по Френкелю, по Фурье, плоские, объёмные, отражательные и т.п.), и разные приёмы получения голограмм и восстановления изображений (в монохроматическом, квазимонохроматическом и белом свете, с малыми или большими углами между опорными пучком S₁ и волной от объекта S₂ - вплоть почти до встречных пучков); здесь и разные свойства голографических изображений (их объёмность; псевдоскопичность действительного изображения и способы её преодоления; увеличение и аберрации при разных формах опорной волны, а также при не параксиальных, а широких пучках; поведение изображений при различных переворачиваниях голограммы и т.д.), здесь и цветное голографирование, и вопросы разрешающей силы как в самих волновых полях, так и в эмульсиях, и разные применения голографии - в интерферометрии (в том числе поляризационной), в изучении тех или иных объектов, например, взвесей, прозрачных рефракционных структур и т.п. Но у слушателей впереди пятидневная школа, где все, что я назвал, плюс многое другое, будет подробно освещено в специальных лекциях. Я могу поэтому позволить себе отказаться от систематичности и остановиться лишь на одном-двух вопросах по выбору, руководствуясь собственным вкусом.

Вернёмся к вопросу об опорном "фазовом рельефе" j ₁(х,у), наличие которого позволяет создать интенсивность, зависящую от разности фаз j ₂(х,у)-j ₁(х,у), и, записав эту интенсивность на фотоплёнку, получить голограмму. В оптике j ₁ это всегда вторая волна, падающая на эмульсию извне. Я уже говорил, что этот путь открыт для голографии и в радио, и в акустике, где с 1966 г. голографических работ появляется асе больше. Но здесь, в другом диапазоне частот, имеется совсем иная возможность создания j ₁(х,у), которую очень хорошо описал Дежан (G.A.Deschamps, Proc.IEEE, 55, №4, 570 (1967)) и которая в работах по акустической голографии уже была применена на деле.

У нас нет эмульсий для радио или звуковых волн, да и площадь голограммы, если требовать мало-мальски приличного разрешения, должна быть здесь довольно велика. Поэтому применяется сканирование; волна от объекта просматривается строка за строкой приёмным рупором, если речь вдет о радиодиапазоне СВЧ, или микрофоном - в акустике. Получается осциллограмма колебания a₁e^-i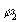. Конечно, механическое сканирование - это, говоря прямо, анахронизм, но зато опорное колебание a₁e^-i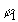 можно подать теперь же в виде второй волны на приёмный рупор или микрофон, а добавить его уже потом - в цепи усиления перед детектором, использовав тот же генератор, который "освещает" объект.

Можно при этом задать любую программу связи j ₁ с координатами (х,у) сканирующего рупора или микрофона, т.е. задать любой закон j ₁(х,у), имитирующий либо плоскую, либо сферическую, либо даже диффузную волну на голограмме. Конечно, этот закон j ₁(х,у) должен храниться для последующего воспроизведения изображения, для восстанавливающего пучка.

Мы имеем здесь пример системы, равносильной "хронизованной" эмульсии: опорное колебание подаётся не извне, а встроено внутрь приёмника.

Радиотехника даёт и ещё одну замечательную возможность. С детектора после УПЧ мы можем отфильтровать чистое произведение H₁(x,y)=ReS₁^*S₂, без ï S_1ï ² и ï S_2ï ², т.е. можем отсечь все то, что неизбежно добавляется в оптической голограмме из-за нелинейного (квадратичного) закона почернения. Изменив фазу S₁ на +90⁰, можно одновременно, после другого детектора, отфильтровать H₂(x,y) = (-iReS₁^*S₂)=ImS₁^*S₂. Мы получаем "комплексную голограмму". При восстановлении изображения уже в оптическом диапазоне простой интерферометр позволяет сложить обе компоненты, используя для Н₁ восстанавливающий пучок S₁, а для Н₂ - тот же восстанавливающий пучок, но сдвинутый по фазе на 90°:

S₁H₁+iS₁H₂=S₁(ReS₁S₂^*+iImS₁^*S₂)=S₁S₁^*S₂=I₂S₂=I₂a₂e^-i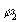

Интерферометр очень прост (рис.2): Н₁ и Н₂ - это переменные коэффициенты отражения его зеркал, а сдвиг S₁ на 90° в одном плече достигается просто перемещением одного из зеркал. Но я хочу обратить ваше внимание на результат: мы получили идеал - восстановление волнового фронта волны от объекта и только этого фронта. Другими словами, мы имеем единственный дифракционный пучок, единственное изображение - мнимое изображение объекта, как это было бы у эмульсии, чувствительной не только к амплитуде, но и к фазе.

В связи с этим я хотел бы сделать в заключение одно побочное замечание. Не следует думать, что в оптике возможны только такие дифракционные решётки, которые дают минимум два спектра. Как известно, "решётка" с комплексной гармонической пропускаемостью даёт лишь одну дифрагированную волну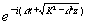. Но где взять такую решётку? Не является ли она лишь математической функцией, используемой для разложений Фурье реальных пропускаемостей? Отнюдь нет.

Если плоская волна e^{-iK(xsinq +zcosq )} падает на плоскую границу двух сред (плоскость z=0), то первичное поле на границе как сверху, так и снизу, пропорционально e^-iKxsinq , т.е. является комплексной гармонической "решёткой". В каждой из сред эта "решётка" порождает по одной дифрагированной волне. Это и

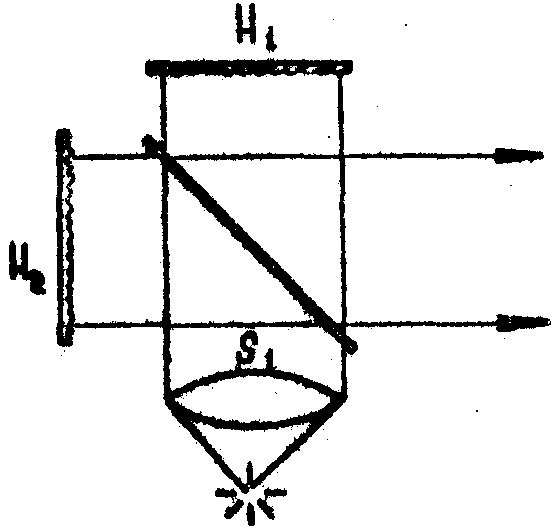
Рио.2. Схема простейшего интерферометра.

есть отраженная и преломленная полны, причём в первой среде, где показатель преломления тот же, что и для первичной волны, угол такой же, а во второй среде, с другим показателем преломления, угол иной. Таким образом, отражение и преломление можно рассматривать как дифракцию на комплексной гармонической решетке.

Описанный способ снятия "комплексной голограммы" тоже даёт нам единственный спектр, но не "скучный" (плоская волна от e^{-ia x}), а несущий в себе закодированное изображение объекта 2.