Влияние временной когерентности на явление дифракции
Рассмотрим структуру волнового поля, которое возникает на плоскости наблюдения p
(рис.8) в результате интерференции волн, приходящих езда из разных точек плоскости источника å
.
Для простоты рассмотрим случай, когда распределение амплитуды вдоль волновой поверхности меняется только вдоль одной координаты h
(явление с одним параметром).
Поле в точке наблюдения Р возникает в результате наложения полей от разных точек М источника. В случае строго монохроматического света амплитуда в Р выражается формулой
¦
(z) = ò
F(g
)exp[i(w
0t-МР)]dg
(8.1)
F(g
) представляет собой распределение амплитуды по волновой поверхности.
Если источник излучает квазимонохроматический свет, то амплитуда в точке Р в момент времени t примет вид
¦
(z,t) = ò
a(t+q
)F(g
)exp[i(w
0t-МР)]dg
(8.2)
Здесь q
- время запаздывания волны, пришедшей в Р из точки М, по сравнению с волной, пришедшей из С.
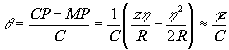 (8.3)
(8.3)
При этом мы пренебрегли членом с h
2, поскольку h
<<z, и заменили h
/R на угол g
.
Начиная отсчёт фаз с фазы колебания, пришедшего в точку Р из точки С, получим
¦ (z,t) = ò
a(t+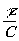 )F(g
)exp[ik0g z)]dg
(8.2)
)F(g
)exp[ik0g z)]dg
(8.2)
так как
2p
(CP-MP)/l
0 = k0g
z (8.5)
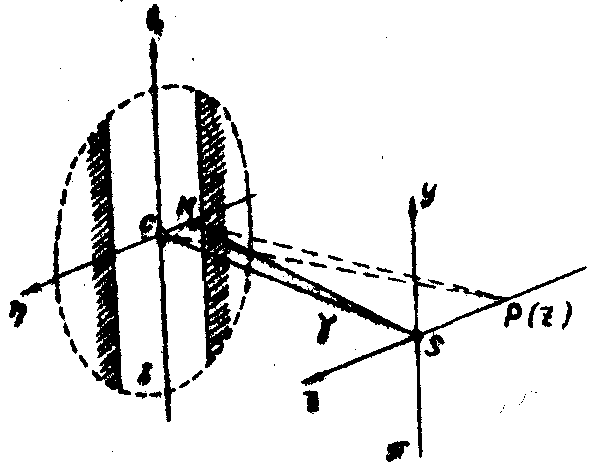
Рис.8.
Интенсивность в точке Р имеет вид:
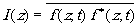 (8.6)
(8.6)
Тогда в соответствии с (8.4) найдем
¦
(z,t)¦
*(z,t) = ò
a(t+g
1z/c)F(g
1)exp[ik0g
1z]dg
1 x
x ò
a*(t+g
2z/c)F*(g
2)exp[-ik0g
2z]dg
2 (8.7)
Полагая g
d=g
1-g
2, можем написать
a(t+g
1z/c)a*(t+g
2z/c) = a(t)a*(t-g
dz/c) = A(g
dz/c)
и
F(g
1)F*(g
2) = F(g
1)F*(g
1-g
d) (8.8)
Усреднение относится только к переменный членам, зависящим от времени. Следовательно,
I(z) = ò
ò
A(g
dz/c)F(g
1)F*(g
1g
d)exp[ik0g
dz]dg
1dg
2 (8.9)
Положим
D(g
1) = ò
F(g
)F*(g
-g
d)dg
(8.10)
Здесь D(g
d)- автокорреляционная функция F(g
). Тогда интенсивность в точке Р равна
I(z) = ò
D(g
d)A(g
dz/c)exp[ik0g
dz]dg
d (8.11)
Если свет строго монохроматичен, то цуги волн бесконечно длинны и
A(g
dz/c) = 1
тогда
I(z) = ò
D(g
d)exp[ik0g
dz]dg
d (8.12)
Интенсивность в точке Р равна преобразованию Фурье от автокорреляционной функции для F(g
).
В качестве конкретного примера на явление с одним параметром рассмотрим задачу о дифракции на щели. Пусть
F(g
) = 1 для -g
0 £
g
£
g
0
F(y) = 0 для |
g
|
> g
0 (8.13)
(см.рис.9а).
Так как F(g
)- действительная величина, то согласно формуле (8.10) D(g
d) будет представлена участком АВ, общим для обеих щелей шириной 2g
0 и смещённых друг относительно друга на величину g
d.
Пусть свет, излучённый источником, представляет собой ограниченные цуги синусоидальных волн частотой u
и продолжительностью t
. Для каждого цуга в течение времени t
комплексная амплитуда постоянна и равна единице.
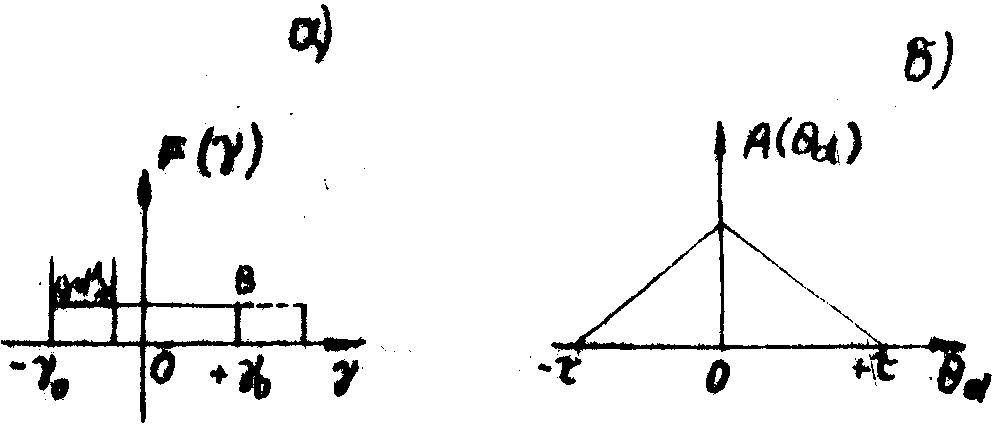
Рис.9.
Спектр, излучаемый источником, выражается формулой (2.4),
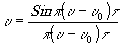
Так как a(t) постоянно, то
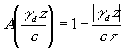 (8.14)
(8.14)
 представляет собой
время q
d,
которое должно быть меньше t
, чтобы
представляет собой
время q
d,
которое должно быть меньше t
, чтобы
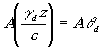
не было равно нулю (рис.9б). Функция А(q
d) называется коэффициентом временной когерентности. Он равен нулю, если |
q
d|
>t
, так как в этом случае цуги не перекрываются.
Положим
g
d = kg
0 (8.15)
Коэффициент временной когерентности теперь имеет вид
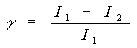 -2
£ x £ 2 (8.16)
-2
£ x £ 2 (8.16)
где ℓ=сt
- длина цугов волн. Точно так же
D(g
d) = D(x) = 1 – |
x/2|
, -2 £
Х £
2 (8.17)
Формула (8.11) дает
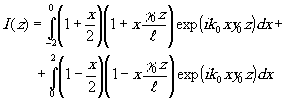
Обозначая k0y0z=Z, получим
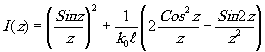 (8.18)
(8.18)
Здесь ℓ - длина когерентности.
Кривая 1 на рис.10 представляет интенсивность дифракционного изображения щели (первый член в правой части уравнения (8.18)). Кривая 2 описывает изменения второго члена, в (8.18).
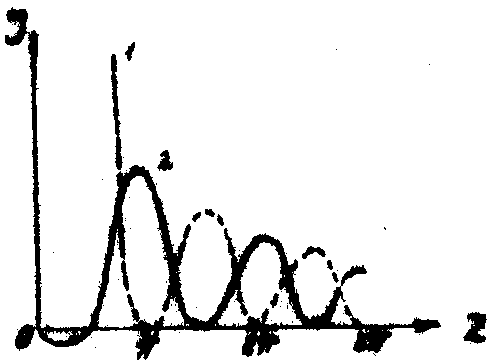
Рис.10. Зависимость интенсивности дифракционного изображения щели от Z.
При z>p
/2 он всегда положителен. Рисунок 10 и формула (8.18) показывают, какое влияние оказывает длина цуга на структуру светового поля при дифракции на щели.
Если ℓ→¥
(монохроматический свет), то в правой
части остаётся только член 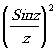 .
Когда цуги имеют конечную длину, то к
ординатам кривой 1
следует прибавить ординаты кривой 2,
умноженные на соответствующую величину.
Практически максимумы величины 2 соответствуют
нулевым минимумам кривой 1
и наоборот. Второй член стремится нивелировать интенсивности полос, окружающих
центральное пятно.
.
Когда цуги имеют конечную длину, то к
ординатам кривой 1
следует прибавить ординаты кривой 2,
умноженные на соответствующую величину.
Практически максимумы величины 2 соответствуют
нулевым минимумам кривой 1
и наоборот. Второй член стремится нивелировать интенсивности полос, окружающих
центральное пятно.

