КАЧЕСТВО ОПТИЧЕСКОГО ИЗОБРАЖЕНИЯ
П.Ф.Паршин
В в е д е н и е
В предлагаемом обзоре рассматриваемая ряд вопросов теории, которые условно можно отнести к проблеме качества оптического изображения. Основное внимание было уделено обсуждению результатов дифракционной теории аберраций, хотя геометрическая теория аберраций, несомненно, применима при построении изображений во многих приложениях. Однако обращение к последней связано с изложением многих понятий геометрической оптики, что значительно увеличило бы объём рукописи и однородность изложения. Поэтому читателям, интересующимся этими вопросами, мы предлагаем обратиться к любым учебникам, посвящённым общим вопросам геометрической оптики.
При изложении вопросов главное внимание было сосредоточено на обсуждении основных положений теории и их недостатков; что же касается иллюстраций, то здесь автор предпочитал отсылать читателя к соответствующим книгам, где их можно было найти. Такой стиль изложения кажется более экономным и даёт возможность больше сосредоточить внимание на сущности рассматриваемых вопросов.
1. Скалярная теория дифракции
При рассмотрении задач дифракции обычно используют представление о том, что составляющие напряжённости электрического и магнитного векторов электромагнитного поля удовлетворяют дифференциальному уравнению второго порядка гиперболического типа:
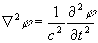 (1)
(1)
Далее решение ищется в виде интеграла
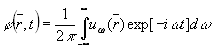 (2)
(2)
После подстановки (2) в (1) получаем уравнение Гельмгольца:
Ñ 2Uw
+k2Uw =0, k=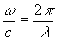 (5)
(5)
Для решения последнего используют вспомогательное решение для функции Грина:
Ñ
2b+k2b=-d
(r-r')
Тогда получают знаменитое кирхгофовское решение для стационарного поля в точке наблюдения Q в виде:
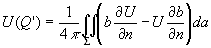 (4)
(4)
где под поверхностью интегрирования å
следует понимать открытую поверхность, на которой образуются вторичные волны Гюйгенса. Обычно это апертура прибора.
При решении задач дифракции основные трудности и погрешности возникают при дальнейшем упрощении (4) с целью выполнения практического интегрирования.
Однако, прежде чем мы перейдём к дальнейшим преобразованиям (4), сделаем ряд замечаний общего характера.
Во-первых, скалярная теория дифракции, приводящая к решению уравнения (1), далека от реальности, ибо на практике имеют дело с неполяризованным светом. Общее решение задачи в векторном приближении рассматривалось в работах Игнатовского /1/, Фока /2/. К сожалению, пока практического применения эти работы не нашли и, несмотря на их давность, до сих пор остаются почти единственными уникальными исследованиями в этом направлении.
Во-вторых, обычно рассматривается монохроматическое приближение, т.е. решается уравнение (3), а не (1), тогда как на практике обычно имеют дело с немонохроматическим светом.
Здесь хотелось бы также подчеркнуть, что в настоящее время в связи с успехами теории частичной когерентности и особенно с бурным развитием голографии теория дифракции переживает период "возрождения", и, в частности, строгие решения задач дифракции привлекают всё более пристальное внимание.
Вернёмся теперь снова к решению уравнения
(4). Обычно при вычислении
(4) применяют конструктивный метод построения
функции Грина, предложенный Зоммерфельдом /3/. Он показал, что задача дифракции
будет поставлена некорректно, если потребовать, чтобы на поверхности å
одновременно были бы заданы потенциал
U и производная во нормали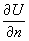 .
Этого можно избежать, если найти такую
функцию G, которая
на поверхности å
будет, например, обращаться в нуль,
т.е. G(å
)=0. Для случая плоской границы раздела
такую функцию можно сконструировать в форме
.
Этого можно избежать, если найти такую
функцию G, которая
на поверхности å
будет, например, обращаться в нуль,
т.е. G(å
)=0. Для случая плоской границы раздела
такую функцию можно сконструировать в форме
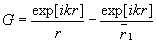 (5)
(5)
где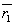 -
радиус -
вектор от точки Q'
до поверхности å .
Из (5) находим,
что
-
радиус -
вектор от точки Q'
до поверхности å .
Из (5) находим,
что
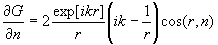 (6)
(6)
Предполагая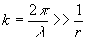 и
Cos(r,n)» 1, заменяют
(6) на
и
Cos(r,n)» 1, заменяют
(6) на
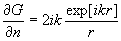 (6')
(6')
и тогда после подстановки (6') в (4) находят
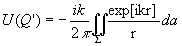 (7)
(7)
Следует особо обратить внимание на тот факт, что уравнение (7) выведено при предположении, что å
- плоская поверхность. Часто об этом забывают (см., например, рассмотрение этого вопроса в книге 0'Нейла /4/) и используют в дальнейших преобразованиях (7), предполагая, что å
имеет сферическую или любую другую форму.
В книге Марешаля и Франсона /5/ при пользовании формулой (7) не ссылаются на вывод Зоммерфельда, а воспроизводят в общих чертах вывод Крозе, Дариуа и Дюрана /6/, а также Робье /7/, получивших формулу, аналогичную (7). В этих выводах поверхность å
может иметь произвольную форму.
В книге Борна и Вольфа /8/ предполагается, само собой очевидным, возможность замены плоской границы раздела, совпадающей с плоскостью диафрагмы, на любую другую (например, сферическую) поверхность, если только потребовать сохранения прежнего контура, ограничивающего исходную апертуру. Однако этот результат не согласуется с данными Менахем и Шиффера в сборнике /9/ по теории дифференциальных уравнений эллиптического типа. Эти авторы, в частности, указывают на изменение функции Грина с изменением геометрической формы области или, что то же самое, граничной поверхности при рассмотрении задач, посвящённых электромагнитному полю. К сожалений, их результаты представлены в весьма обобщённой форме и их трудно применить для практических оценок.
Формула (7) является исходной в теории голографии. Однако в книге Строука /10/, к сожалению, обсуждению формулы (7) посвящено очень мало места и читателю, интересующемуся подробностями, предлагается обратиться к книге Марешаля и Франсона.
Таким образом, становится очевидным, что вывод формулы (7) недостаточно полно освещен в литературе и границы её применимости пока не выяснены.
Следующий шаг в решении (7) состоит в предположении, что U(å
) всюду равна нулю на границе области å
и диафрагма не оказывает никакого влияния на внешнее поле излучения. Такое предположение значительно облегчает практическое применение в дальнейшем формулы (7), но совершенно не применимо при выводе предельных соотношений. В частности, неоднозначность решения обратной задачи в теории дифракции (восстановление объекта по полю излучения) является прямым следствием этого предположения. Широко распространённое мнение о том, что дифракционное размытие изображения является принципиальным ограничением на пути увеличения разрешения, является прямым следствием этого предположения.
Следующее упрощение состоит в разложении;
r2 =(x-u)2+(y-v)2+w2 »
R2+x2+y2-2(ux+vy) (8)
или
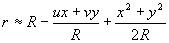 (9)
(9)
Однако и этого приближения для выполнения аналитических вычислений оказывается недостаточно даже в простейших случаях. Поэтому здесь различают два основных приближения.
1. Фраунгоферова дифракция:
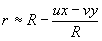 (10)
(10)
полученная при предположении, что x2<<R и y2<<R. Для практической реализации этого условия обычно применяют фокусирующие объективы, которые дают возможность как бы наблюдать явление дифракции на бесконечности. Однако такой способ может оказаться не всегда приемлемым, особенно в ИК области из-за сильного поглощения преломляющих материалов, а также из-за дополнительных аберраций. В связи с этим представляет большой практический интерес получение фраунгоферовой дифракции с помощью системы френелевских зонных пластин, названных "френелевским сендвичем", рассмотренное в книге Мерца /11/.
2. Френелевская дифракция:
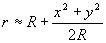 (9)
(9)
В этом случае предполагается, что |ux-vy|<<R . Для наблюдения дифракции достаточно рассматривать распределение освещенности на расстояниях R, сравнимых с размерами апертуры. В связи с задачами голографии в настоящее время это приближение приобрело
особое значение. На его основе в последние годы была создана теория "преобразования Френеля", с помощью которой удаётся качественно достаточно просто рассмотреть процессы образования изображений в голографии. Однако при анализе оптических систем обычно применяют Фраунгоферово приближение, которое в дальнейшем будет только рассматриваться.
Итак, подставим (10) в (7), тогда
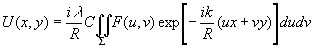 (12)
(12)
где через С обозначен численный множитель, выражение для которого нетрудно получить. Под (х,у) следует понимать координаты в плоскости наблюдения дифракционной картины.
Так как ранее было предположено, что U(å
)=0 (поле равно нулю на контуре, ограничивающем область å
), то формулу (12) можно переписать теперь в виде
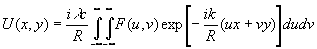 (15)
(15)
при дополнительном условии: F(u,v) определяет поле возмущения по зрачку и F(u,v)=0 вне области å
и на её границе. Формула (15) является исходной при анализе формирования оптических изображений как в когерентном, так и некогерентном свете.
2. Дифракционная теория аберраций
Аберрационная теория, которая является одной из наиболее важных основ геометрической оптики, с тех пор как Гамильтон в 1827 г. ввел в оптику понятие характеристической функции, связав её с оптической длиной луча, постепенно систематизировалась. Так как метод, связанный с применением этой теории, весьма аналогичен методу аналитической механики, развитому Лагранжем, то Гамильтон смог перенести этот метод к общим проблемам механики и таким образом вывести знаменитое уравнение движения, названное его именем. Однако его работа в оптике, как об этом пишет Миамото /12/, долгое время оставалась мало известной и снова приобрела известность после того, как был создан эйконал Брамса, который принёс практические результаты. Так в 1905 году аберрационная теория Зайделя была усовершенствована и систематизирована Шварцшильдом. В соответствии с этой теорией оказалось, что характеристическая функция является наиболее важным понятием геометрической оптики даже с исторической точки зрения. Связь между этой характеристической функцией и волнами была найдена в 1911 году Зоммерфельдом и Рунге. Они показали, воспользовавшись идеями Дебая, что волновое уравнение становится дифференциальным уравнением для характеристической функции при l
→0.
Однако, когда аберрации достаточно малы, формирование изображения должно быть анализировано на основе дифракционной теории.
Первые исследования в направлении учёта аберраций при формировании изображений на основе волновой оптики были выполнены Пихтом /13/ и Стивардом /14/. Однако наибольших успехов в решении этой задачи добился Нейбор /15/, который ввёл понятие волновой аберрационной функции, полученной как разность хода, образованной между точками реальной волновой поверхности и сферы сравнения. Эту функцию мы будем обозначать через V(u,v) в формуле /11/.
Нейбор связал геометрическую оптическую аберрацию с волновой аберрационной функцией V(u,v), рассмотрев уравнение для нормалей к деформированной волновой поверхности. В результате было найдено что геометрические аберрации в гауссовой плоскости (х,u) связаны с функцией V(u,v) уравнениями
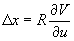 и
и 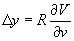 (14)
(14)
В общем случае при малых аберрациях связь V(u,v) с аберрационными коэффициентами была найдена Стивардом /14/. Если вместо декартовых координат (u,v) ввести полярные (r
,j
), то функцию V(r
,j
) можно разложить в ряд по r
nCosmj
. Тогда получим /4/
V(r
,j
)=a0+b0h2+b1r
2+b2hr
Cosj
+С0h4+С1r
4+... (15)
где h - смещение геометрического изображения точки относительно оптической оси системы в гауссовой плоскости (см.рис.4.1. на стp.81 в /4/).
Цернике и Нейбор /16/ предложили разложение V(r
,j
) по полиномам специального вида Rnm(r
)Cosmj
:
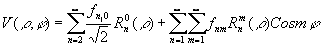 (l6)
(l6)
Это разложение примечательно тем, что выполнено по ортогональной системе функций. Действительно, как это следует из условия, для ортогональности
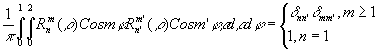 (17)
(17)
Rnm(r
)Cosmj
ортогональны на единичной окружности. Общее выражение для этих полиномов приводится в книге Борна и Вольфа /8/ на стр.465, там же можно найти частные представления этих полиномов. Если с помощью такого разложения вычислить средний квадрат деформации волнового фронта Е0, то получим
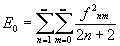 (18)
(18)
которое является суммой положительных линейно независимых величин. Таким образом, при деформации волнового фронта надо ставить вопрос не о компенсации аберраций, а об уменьшении до нуля возможно большего числа членов ¦
nm. Показано, что если рассматривать в отдельности полиномы Rnm(r
), то они соответствуют волновому фронту с минимальным среднеквадратичным отступлением от идеальной сферы /4/
Большой интерес представляет классификация волновых аберраций на основе этого типа разложения, предложенная Нейбором.
3. Формирование изображений оптическими системами
При рассмотрении этой проблемы следует выделить два наиболее важных аспекта. Прежде всего при построении изображения, получаемого в оптической системе, приходится всегда искать компромиссное решение о сочетании геометрической теории и волновой.
Рассмотрим, в чём состоит сущность геометрической теории при построении изображений. Предположим, что источник излучает монохроматический свет из некоторой точки, расположенной на конечном расстоянии от оптической системы. По законам геометрической оптики для любой заданной системы мы можем рассчитать положения точек пересечения лучей с плоскостью изображений, выходящих из источника под разными углами. Геометрическая оптика идентифицирует интенсивность света в плоскости изображения с плотностью этих лучей пересечения. Очевидно, что при современных возможностях электронно-вычислительной техники такие расчёты вполне доступны. Однако при интерпретации результатов возникают принципиальные трудности, обусловленные приближённостью геометрической теории, основанной на предположении, что длина волны равна нулю. Расхождение теории с практикой становится особенно значительным при приближении к идеальным оптическим системам с аберрациями, близкими к нулю. В этом случае по законам геометрической оптики фронт волны, распространяющийся в направлении плоскости изображений, будет иметь почти сферическую форму и в результате в изображении получится точка с бесконечной интенсивностью.
В случае оптической системы, близкой к идеальной, более надёжные результаты даёт расчёт на основе волновой оптики, позволяющей учесть явление дифракции. По-видимому, первый такой расчёт был выполнен в 1835 году Эри, который вывел формулу для распределения освещённости в фраунгоферовом приближении при учёте только дифракции плоской волны на круглом отверстии и наблюдении в гауссовой плоскости. В этом случае получается классическая формула Эри, показывающая, что вместо светящейся точки получается пятно с центральным ядром и с быстро загасающей системой концентрических колец. К сожалению, при некотором отступлении от гауссовой плоскости наблюдения формула для расчёта освещённости значительно усложняется. Соответствующие формулы для этого случая можно найти в обзоре Вольфа /17/, а также в книге Борна и Вольфа /8/. Дальнейшее развитие теории при рассмотрении малых аберраций (доля длины волны) идёт по пути модернизированная волновой оптики при расчёте интенсивности света.
Нейбор в 1949 году, воспользовавшись разложением (16) для волновой аберрационной функции, смог вычислить распределение освещённости в гауссовой плоскости, для малых аберраций. В частности, им совместно с Цернике /16/, а также Нейнхаузом /18/ были впервые вычислены и построены кривые равной интенсивности (изофотографии) при наличии сферической аберрации и комы. Фотографии, хорошо иллюстрирующие результаты этих расчётов, можно найти в книге Борна и Вольфа /8/ на стр.478-480. Большое количество аналогичных расчётов выполнено Линфутом /19/.
В случае, когда волновые аберрации больше длины волны, вычисление освещённости для отдельных типов аберраций значительно усложняется, так как при разложении экспоненты, входящей в выражение для подынтегральной функции в исходной для расчёта формуле (см. стр.473 в /8/), необходимо учитывать, кроме первого, ещё и последующие члены разложения. Расчёты для этого случая можно выполнить на специализированной машине. Такие расчёты впервые были выполнены Марешалем /20/ в 1948 году. Описание машины и полученных результатов можно такие найти в книге Марешаля и Франсона /5/ и в книге Линфута /19/.
Действия больших аберраций были успешно рассмотрены Ван Кампеном /21/ в 1949 году, применившим метод стационарной фазы к интегралу Кирхгофа. В результате ему удалось вывести асимптотическое разложение этого интеграла в предельном случае l
→0. Найденный результат можно интерпретировать как вклад "геометрической оптики", но учитывающий взаимную интерференцию частичных волн, соответствующих ближайшей окрестности седловых точек первого рода в методе стационарной фазы. Достаточно подробный вывод его формул можно найти в обзоре Миамото /12/, ряд важных критических замечаний приведен Вольфом /17/.
Из двух указанных в начале этого параграфа аспектов проблемы формирования изображения мы рассмотрели выше только одну, касающуюся волновой природы света.
Второй не менее важный аспект касается понятия когерентности света. В связи с созданием лазеров голографии вопросы, относящиеся к когеренции света, приобрели в настоящее время большое научное и практическое значение. Для развития теории большое значение имеет идея Вольфа, предложившего для учёта реально измеряемых величин в оптике ввести понятие функции взаимной когеренции, впоследствии названной его именем. При феноменологическом рассмотрении процессов, приводящих к возможности наблюдения распределения интенсивности света в любых точках пространства, эту функцию, следуя обозначениям 0'Нейла /4/ (см. форм. (8.3) на стр.186), можно записать в виде
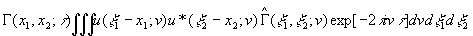
В этой формуле х1 и х2 - обобщённые координаты любых двух точек в пространстве, x
1 и x
2 - обобщенные переменные интегрирования; при этом область интегрирования определяется областью задания подынтегральных функций.
Физический смысл этой формулы состоит в том, что из электромагнитных полей от двух точек объектива можно составить функцию взаимной корреляции, которая является основной формулой при выводе выражения для интенсивности света в любого типа оптических приборах.
Интенсивность в точке из этой формулы найдём при предельном
переходе х1→х2
и t →0.
Для упрощения (18)
обычно пользуются квазимонохроматическим
приближением, считая, что D u
<<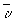 ,
где
,
где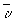 -
средняя частота излучения, D u
-
ширина спектральной полосы. Кроме этого, делаются дополнительные предположения
о свойствах объекта, а именно: полагают, что либо Г(x
1,x
2;0)= А(x
1)А2(x
2), либо Г(x
1,x
2;0)=I(x 1)d
(x 1-x
2). Соответственно,
этим двум случаям из (18)
выводятся всем хорошо знакомые формулы для расчёта освещённости при когерентном
и некогерентном освещении объекта.
-
средняя частота излучения, D u
-
ширина спектральной полосы. Кроме этого, делаются дополнительные предположения
о свойствах объекта, а именно: полагают, что либо Г(x
1,x
2;0)= А(x
1)А2(x
2), либо Г(x
1,x
2;0)=I(x 1)d
(x 1-x
2). Соответственно,
этим двум случаям из (18)
выводятся всем хорошо знакомые формулы для расчёта освещённости при когерентном
и некогерентном освещении объекта.
Применение этой теории к обычным оптическим системам показывает,
что когерентное освещение просто можно получить, освещая любой предмет излучением
от лазера, причём заметим, что, как показал 0'Нейл /4/, оптическая система при
таком освещении приобретает ряд дополнительных (фильтрующих) свойств, позволяющих
улучшать качество изображений. С другой стороны, некогерентное освещение в "чистом
виде" можно получить, если сам объект наблюдения достаточно больших размеров
является непосредственно источником излучения. В подавляющем числе случаев свет
от объекта, поступающий в объектив прибора, всегда содержит часть излучения,
которое можно считать когерентным, и другую часть
- некогерентную. Для того, чтобы на практике
избавиться от когерентного света возможно применить специальные диффузные рассеятели
света. Важно обратить внимание ещё на тот факт, что
оба
рассматриваемые приближения используют
предположение о спектральной узости полосы излучения, т.е. D
u <<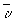 .
Такое предположение на самом деле не имеет место при облучении оптической системы
белым светом. Часто об этом забывают и выводы о качестве изображения, полученные
для заданной длины волны, автоматически обобщают на случай, когда оптическая
система работает при
дневном свете.
.
Такое предположение на самом деле не имеет место при облучении оптической системы
белым светом. Часто об этом забывают и выводы о качестве изображения, полученные
для заданной длины волны, автоматически обобщают на случай, когда оптическая
система работает при
дневном свете.
В связи с этим для расчёта освещённости при немонохроматическом освещении в некогерентном приближении предлагается вместо обычного расчёта по формуле
S(x,y)→u(x,y)u*(x,y) (19)
выполнять расчёт по формуле
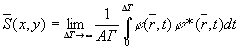 (20)
(20)
где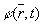 определяется
по формуле (2).
определяется
по формуле (2).
К сожалению, на этот вопрос в литературе, по-видимому, мало обращали внимания, хотя он имеет большое практическое значение.
4. Изображение протяженных объектов и
передаточная функция оптического прибора
До сих пор мы рассматривали получение изображений точечных источников. Теперь мы опишем некоторые общие методы, основанные на технике преобразования Фурье, которые применяются при анализе формирования изображений протяженных объектов. Эти методы были первоначально разработаны главным образом Дюфье /22/.
Рассмотрим образование изображения сначала при когерентном освещении.
В этом случае, если через U0(х0,у0) обозначить комплексное распределение в плоскости объектов, а через К(х0,у0;х1,у1) амплитудную функцию рассеяния, которая характеризует оптические свойства системы, то результирующее распределение в точке (х1,у1) будет определяться выражением
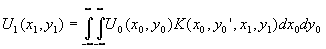 (21)
(21)
В этой формуле вместо старых обозначений (х,у) для декартовой системы координат введены обозначения (х0,у0), которые учитывают изменение масштаба при увеличении. Так, если предмет в оптической системе изображается с увеличением М и (х0,у0) - координаты точки этого предмета в плоскости объектов, то х0=МХ0 и у0=MY0. Иногда при пользовании формулой (21) удобно также считать U0(х0,у0) "идеальным геометрическим изображением" объекта в Гауссовой плоскости.
Обычно вместо уравнения (21) рассматривают интегральное уравнение, в котором ядро уравнения К(х0,у0',х1,у1) зависит от разности двух аргументов
К(х0,у0',х1,у1) = КА(х1-х0,у1-у0) (22)
Такое упрощение связано с введением понятия "изопланатической области А".
Рассмотрим, в каком случае имеет место (22).
Известно, что в хорошо скорректированных оптических системах волновые аберрации изменяются весьма медленно, когда точка объекта Р(х0,у0) перемещается по рабочему полю. Это поле может быть разделено на области, в каждой из которых волновые аберрации (измеренные от сферы, центрированной в точке идеального изображения) достаточно постоянные или, как говорят иногда, эффективно постоянные. Под этим подразумевается, что сохраняются неизменными усреднённые значения волновых аберраций на определённых участках сферы сравнения, соответствующих области А. Иногда допускают ошибку и считают, что под изопланатической областью понимается область, в которой волновые аберрации, а не их усреднённые значения не изменяются при смещении положения точки Р(х0,у0). Подробное обсуждении свойства изопланатизма можно найти в работе Даймонта /23/, а также в книге Линфута /24/.
Ограничимся теперь рассмотрением только таких объектов, размеры которых столь малы, что они не выходят за границы изопланатической области. Тогда уравнение (21) можно переписать в виде
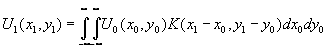 (23)
(23)
где К(х1-х0,у1-у0)
можно представить в форме 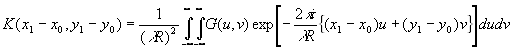 (24)
(24)
где R -
радиус сферы сравнения, а функция G(u,v)
содержит амплитудные и фазовые изменения по сфере сравнения. Выражение
(24) ясно показывает, что функцию К(х1-х0,у1-у0)
можно интерпретировать как Фурье-образ
G(u,v), а следовательно, кажется весьма
заманчивым, применить ко всем рассматриваемым функциям
U1, К,
U0 преобразование Фурье. Представим,
например, U0(x0,у0)
через интеграл Фурье от функции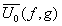 :
:
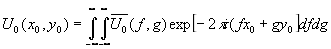 (25)
(25)
или в операторной записи:
U0(x0,y0)=T[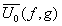 ] (26)
] (26)
Аналогичным образом можно представить и другие рассматриваемые функции. На основании теоремы о свертке мы найдём:
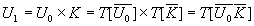
откуда
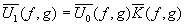 (27)
(27)
Это уравнение означает, что если рассмотреть в отдельности
отображение распределений в плоскости объекта и в плоскости изображений в пространстве
пространственных частот (¦
,g), то тогда переход от объекта к изображению
эквивалентен действию линейного фильтра, а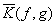 выполняет
роль пропускания оптической системы как функция пространственных частот.
выполняет
роль пропускания оптической системы как функция пространственных частот.
Полученный результат имеет исключительно важное значение, ибо благодаря ему оптику можно рассматривать как раздел радиоэлектроники.
Широкое обсуждение различных вопросов оптики о точки зрения радиоэлектроники представлено в книге 0'Нейла /4/, а также в книге Строука /10/, в которых главным образом рассматриваются проблемы голографии.
Другой важный результат получается, если мы снова обратимся к формуле (24). Очевидно, что
К(х,у)=Т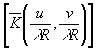 =G(u,v) (28)
=G(u,v) (28)
и, следовательно, частотная передаточная функция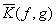 для
когерентного освещения эквивалентна значению зрачковой функции G(u,v)
в точках u=l
R¦ и
v=l Rg
Гауссовой сферы сравнения.
Этот результат для голографии имеет исключительно
важное значение, ибо позволяет легко осуществлять фильтрацию пространственных
частот рассматриваемого объекта посредством наложения соответствующих масок
в плоскости зрачка. В микроскопии при освещении предметов монохроматическим
светом помещение соответствующей маски, не пропускающей некоторые пространственные
частоты, позволило Аббе /25/ в методе двойной дифракции увеличить в два раза
число линий линейной миры, разрешаемых на единицу длины. Теперь обратим внимание,
что спектр пространственных частот всегда оказывается ограниченным. Действительно,
так как G(u,v)=0 вне
апертуры зрачка, то
для
когерентного освещения эквивалентна значению зрачковой функции G(u,v)
в точках u=l
R¦ и
v=l Rg
Гауссовой сферы сравнения.
Этот результат для голографии имеет исключительно
важное значение, ибо позволяет легко осуществлять фильтрацию пространственных
частот рассматриваемого объекта посредством наложения соответствующих масок
в плоскости зрачка. В микроскопии при освещении предметов монохроматическим
светом помещение соответствующей маски, не пропускающей некоторые пространственные
частоты, позволило Аббе /25/ в методе двойной дифракции увеличить в два раза
число линий линейной миры, разрешаемых на единицу длины. Теперь обратим внимание,
что спектр пространственных частот всегда оказывается ограниченным. Действительно,
так как G(u,v)=0 вне
апертуры зрачка, то
u2 + v2 £
а2
откуда
¦ 2 + g2
£ 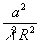
В случае круглого отверстия
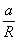 =Sinq
, где
q - апертурный
угол, откуда
=Sinq
, где
q - апертурный
угол, откуда
¦ 2 + g2
£ 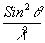
Особый интерес представляет рассмотрение оптических систем, обладающих круговой симметрией. В этом случае вместо преобразования Фурье следует применить преобразование Фурье-Бесселя.
При таком преобразовании U0(x0,y0)=U0(r) уже можно представить через одинарный интеграл в виде
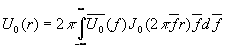 (29)
(29)
а, в свою очередь,
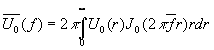 (30)
(30)
Здесь оказалось целесообразным перейти к полярным координатам:
x=rCosj ; y=rSinj
; 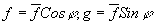 .
По аналогии с несимметричным случаем можно повторить все вычисления и прийти
к тем же результатам. Однако теперь будет иметь место фактически одномерное
пространство пространственных частот и спектральная полоса пропускания оптической
системы будет ограничена условием
.
По аналогии с несимметричным случаем можно повторить все вычисления и прийти
к тем же результатам. Однако теперь будет иметь место фактически одномерное
пространство пространственных частот и спектральная полоса пропускания оптической
системы будет ограничена условием
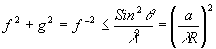
откуда
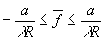 (31)
(31)
Этот результат имеет простую физическую интерпретацию, которая следует из рассмотрения следующего примера.
Рассмотрим одномерный объект, имеющий вид синусоидальной миры. Пусть D
y0 - период, соответствующий частоте g, а свойства объекта в направлении х не изменяются. Тогда из (31) следует, что оптическая система будет пропускать информацию о спектральных компонентах, для которых
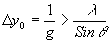 (32)
(32)
где Sinq
- синус полуапертурного угла со стороны изображения.
Рассмотрим теперь формирование изображений при некогерентном освещении. В этом случае в соответствии с общей теорией частичной когеренции вместо амплитудного спектра, представленного формулой (21), следует рассматривать интенсивность
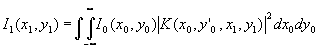 (33)
(33)
Предположим снова, что размеры объекта не выходят из изопланатической области, тогда
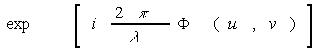 (34)
(34)
В связи с понятием изопланатичности в этом случае следует обратить внимание, что при некогерентном освещении границы области А значительно расширяются, ибо для перехода от (33) к (34) вместо условия (22) достаточно потребовать выполнения более слабого условия
ï
K(x0,y'0,x1,y1)ï
= ï
KA(x1-x0,y1-y0)ï
(35)
Применим к функциям I0, I1, К преобразование Фурье, тогда получим
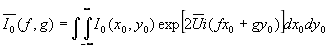
или
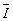 (¦
,g)=T[I0(x0,y0)]
(¦
,g)=T[I0(x0,y0)]
Аналогично будем иметь
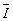 (¦
,g)=T[I1(x,y)] и
L(¦ ,g)=T[ï
K(x,y)ï 2]
(¦
,g)=T[I1(x,y)] и
L(¦ ,g)=T[ï
K(x,y)ï 2]
В силу теоремы о свертке L(¦
,g) можно представить в виде автокорреляционной функции
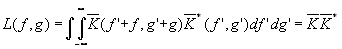 (36)
(36)
Подставив (28) в (36), найдём
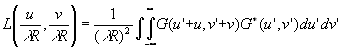 (37)
(37)
Последнее означает, что с точностью до постоянного множителя передаточная частотная функция для некогерентного освещения есть автокорреляционная функция зрачковой функции системы. Подынтегральная функция в (37) будет отлична от нуля только на той части плоскости, где функции G(u'+u,v'+v) и G*(u',v') обе одновременно отличны от нуля. Это будет иметь место только тогда, когда
u2 + v2 £
4a2 (38)
Отсюда получаем ограничение для области частот:
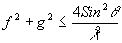
Сравнивая этот случай с предыдущим, мы видим, что область допустимых частот при некогерентном освещении увеличилась в два раза, а наименьший период синусоидальной миры, которую можно наблюдать, будет в два раза меньше.
Для оптических систем с круговой симметрией мы находим
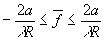 (40)
(40)
При рассмотрении астрономических телескопов удобно вместо
R рассматривать приведённое фокусное
расстояние F=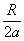 ,
тогда предельная частота спектра
,
тогда предельная частота спектра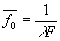 .
Интересно отметить, что при рассмотрении
идеальной оптической системы радиус ядра в картине Эри r0
» 1,22l F.
Отсюда
.
Интересно отметить, что при рассмотрении
идеальной оптической системы радиус ядра в картине Эри r0
» 1,22l F.
Отсюда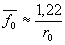 ,
это означает, что предельная частота
аберрационной системы определяется дифракционным пределом
разрешения идеальной оптической системы
с теми же размерами. Гопкинс предложил вместо
,
это означает, что предельная частота
аберрационной системы определяется дифракционным пределом
разрешения идеальной оптической системы
с теми же размерами. Гопкинс предложил вместо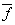 пользоваться
сокращённой линейной частотой
пользоваться
сокращённой линейной частотой
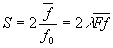 (41)
(41)
До сих пор мы рассматривали формирование изображений только плоских объектов, а следовательно, принципиально не могли учесть влияние соседних объектов, расположенных на отличных расстояниях от объектива по сравнению с рассматриваемым. Однако на практике, например в фотографии, приходятся наблюдать изображение интересуемого предмета на фоне других предметов. В связи с этим представляет несомненный интерес идея Мерца, предложенная им на стр.101 в ег0 книге /11/, в которой он предлагает при рассмотрении передаточных характеристик вводить дополнительный параметр, учитывающий глубину объекта. В частности, он рассмотрел задачу о передаче глубины объекта с помощью идеального цилиндрического объектива. Полученные им результаты пока трудны в интерпретации, однако дальнейшее развитие его идеи может привести к ряду позитивных решений, полезных для практических рекомендаций.
5. Приближенные методы оценки передаточной функции оптической системы
В предыдущем параграфе мы показали, что при анализе формирования изображений протяженных объектов оказалось удобным трактовать оптическую систему как фильтр пространственных частот. При таком рассмотрении приходится вместо анализа распределения освещённости от точечного объекта для характеристики системы находить соответствующее двумерное преобразование Фурье от этого распределения. Такое преобразование Фурье было названо передаточной функцией объекта. Часто вместо передаточной функции объекта используют название частотно-контрастная характеристика, при этом под последней всегда понимается кривая, нормированная на 1 при нулевой частоте.
Рассмотрим теперь некоторые общие вопросы, связанные с приближенными методами расчёта передаточной функции.
После работы Дюфье, привлекшего внимание к передаточной функции, начиная с 50-х годов было опубликовано достаточно много работ, в которых предлагались различные приближенные формулы для расчёта передаточных функций, а также и сами графики этих функций. Большие заслуги в разработке теории принадлежат Гопкинсу /26/. Шаде /27/ внёс значительный вклад в развитие этих идей в области эксперимента.
Обратимся снова к вычислению интеграла (36), однако запишем его в более специальном виде, придерживаясь обозначений, взятых из обзора Миамото /12/:
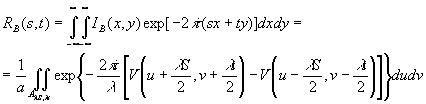 (42)
(42)
Очевидно, что
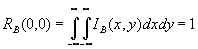 (43)
(43)
Формула (42) получается при предположении, что волновой фронт в оптической системе по сравнению с идеальной сферой сравнения испытывает только фазовые искажения, определяемые функцией V(u,v). При преобразовании (37) была выбрана новая система координат, помещенная в центре области пересечения двух зрачковых функций
G(u'+u,v'+v) и G*(u',v')
Кроме "того, были введены приведённые частоты
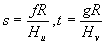 (44)
(44)
где Нu и Нv суть, соответственно, наибольшие значения расстояний координат зрачка в системе декартовых координат (u,v).
Формула (42)
позволяет находить передаточные функции при различных типах аберраций. Для этого
достаточно задать функцию V(u,v)
в явном виде и провести необходимые вычисления. В качестве простого примера
Гопкинс |28|
рассчитал кривые пропускания оптической системы при дефокусировке. В этом случае
волновую аберрационную функцию можно представить в виде
V=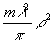 ,
соответствующие кривые для разных m=1,2,3,4
приводятся в книге Вольфа и Борна на стр. 486. Если аберрационную волновую функцию
задать в форме
,
соответствующие кривые для разных m=1,2,3,4
приводятся в книге Вольфа и Борна на стр. 486. Если аберрационную волновую функцию
задать в форме
V(u, v) = A(r
4+Br
2)l
.
то мы учтём зейделевскую сферическую аберрацию и дефокусировку. Расчёты для этого случая выполнены Линфутом /24,29/. Недавно эти результаты дополнил 0'Нейл /4/, который рассчитал кривые пропускания при наличии сферической аберрации как третьего, так и пятого порядков. В своих расчётах волновую аберрационную функцию он задавал в форме
V=d1(r 6
- 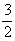 r
20r 4 +
r
20r 4 + 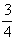 m
r 40r
2)
m
r 40r
2)
где параметры r
0 и m
, соответственно, определяют степень коррекции и установку фокуса, а параметр d1 содержит длину волны.
Выше мы указали только на некоторые расчёты кривых пропускания. На самом деле к настоящему времени достаточно много выполнено и других аналогичных расчетов. Здесь не обсуждаются эти результаты, ибо, во-первых, они представляют слишком частный интерес и далеки от практики, а, во-вторых, это, относится к теме специальной статьи.
Рассмотрим теперь некоторые общие результаты, изложенные в обзоре Миамото /12/, касающиеся понятия передаточной функции в геометрическом приближении. Обратимся снова к формуле (42) и разложим экспоненту в подынтегральной функции в ряд Тейлора в окрестности точки (u,v):
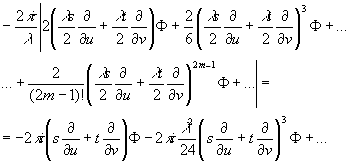 (45)
(45)
Как видно из этого выражения, только первый член в разложении не зависит от l
, а другие члены стремятся к нулю, когда l
→0. Поэтому, сохраняя только первый член в разложении, мы перейдём от волнового приближения передаточной функции RB(s,t) к геометрическому RГ(s,t), определяемому формулой:
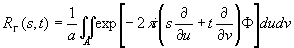 (46)
(46)
Эта же формула такие выводится при применении преобразования Фурье к распределению интенсивности, полученной в приближении геометрической оптики:
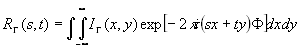 (47)
(47)
Сравнение результатов расчётов RB(s,t) и RГ(s,t) приводилось рядом авторов. Так, Гопкинс /26/ рассматривая дефокусировку линзы, свободной от аберраций, пришёл к вывода, что обе функции достаточно хорошо совпадают в области нижних частот, если волновые аберрации больше 2l
. М. Де /30/ и Бромилов также провели сравнение этих функций при астигматизме и сферической аберрации.
Принципиальным затруднением теории передаточных функций являемся невозможность учёта немонохроматичности излучения. Действительно, обычно все кривые пропускания рассчитываются для заданной длины волны, тогда как обычные оптические системы используются при освещении в белом свете. Более того, анализ рассчитанных кривых пропускания показывает, что при увеличении волновых аберраций на малую долю длины волны форма кривых значительно изменяется, а это означает, что если в спектре источника излучения содержатся достаточно близкие спектральные линии, то они будут оказывать существенное влияние на обобщённую передаточную функцию.
Рассмотрим теперь некоторые вопросы, относящееся к расчёту частотно-контрастных характеристик реальных оптических систем. При составлении программ, с помощью которых вычисляются эти характеристики, возникают трудности как в отношении выбора квадратурной формулы для приближенного вычисления интервалов, так и положения узлов и их числа. При решении этих вопросов составители программ, как правило, руководствуются рядом интуитивных соображений, и в результате после проведения расчётов возникают трудности в оценке точности вычислений. В связи с этим предлагается общий принцип построения самокорректирующих программ вычисления передаточных функций, учитывающий характер изменения волновых аберраций по зрачку и заданную точность вычислений.
Обратимся снова к интегралу
(37) и заметим, что функция зрачка
G(u,v) равна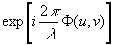 в
области зрачка и нулю вне этой области. В интеграле
(38) на самом деле мы имеем конечную
область интегрирования, которую мы обозначим через D.
Как уже обсуждалось ранее, эта область
представляет собой сегмент, полученный в результате перекрытия двух окружностей,
когда центр одной смещён в точку (u,v)
относительно другой окружности с центром в точке
(0,0) (имеется в виду система с круговой
симметрией).
в
области зрачка и нулю вне этой области. В интеграле
(38) на самом деле мы имеем конечную
область интегрирования, которую мы обозначим через D.
Как уже обсуждалось ранее, эта область
представляет собой сегмент, полученный в результате перекрытия двух окружностей,
когда центр одной смещён в точку (u,v)
относительно другой окружности с центром в точке
(0,0) (имеется в виду система с круговой
симметрией).
Предположим, что вид функции Ф(u,v) известен, и она представлена
достаточно сложной зависимостью от u,v.
Воспользуемся тем обстоятельством, что
подынтегральная функция по модулю не может превзойти 1, а частоты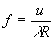 и
и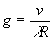 ограничены
условием
ограничены
условием
u2 + v2 = l
2R2(¦
2 + g2) £
4a2
Это даёт возможность при расчёте кривых пропускания применить метод "квантования по уровню", разработанный для интерференционной спектрометрии /31/.
Сделаем следующее преобразование:
G(u'+u,v'+v)G*(u',v')=ехр{i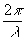 [Ф(u'+u,v'+v)-Ф(u',v')]}(48)
[Ф(u'+u,v'+v)-Ф(u',v')]}(48)
Выберем некоторую новую длину волны l
C<<l
и решим уравнение
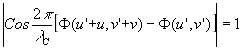 (49)
(49)
Обозначим корни этого уравнения через u'n(u,v) и v'n(u,v). Очевидно, они должны удовлетворять уравнению
Ф(u'+u,v'+v)-Ф(u',v')=±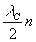 (50)
(50)
при дополнительном условии: u2+ v2 £
4a2.
В результате решения уравнения (50) область интегрирования D окажется покрытой сеткой, полученной соединением прямыми линиями между собой всех точек (u'n,v'n), удовлетворяющих (49).
Буем считать, что точки (u'n,v'n)Î
D все найдены, и для дальнейшего вычисления (37) разобьём область D на элементарные ячейки dn, определяемые условием u'n-1 £
u £
u'n и v'n-1 £
v £
v'n. Тогда вычисление (57) сведётся к сумме интегралов
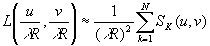 (51)
(51)
где
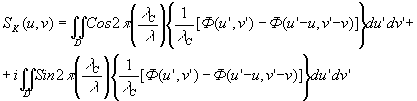 (52)
(52)
Для вычисления SK(u,v)
можно воспользоваться любой квадратурной формулой. Если l
С
достаточно мало, то можно воспользоваться для вычисления
SК(u,v)
квадратурной формулой прямоугольников или трапеции. Обозначим через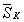 оценки
SK,
полученные приближенным интегрированием, а сумму, полученную в результате замены
SK
на
оценки
SK,
полученные приближенным интегрированием, а сумму, полученную в результате замены
SK
на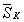 в
(51) через
в
(51) через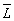 .
Если последовательность чисел
.
Если последовательность чисел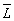 при
l С→0
равномерно сходится к
при
l С→0
равномерно сходится к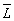 ,
то для оценки точности вычислений можно
воспользоваться тем свойством, что числа
,
то для оценки точности вычислений можно
воспользоваться тем свойством, что числа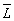 при
последовательном уменьшении l С
будут мало отличаться друг от друга, начиная с некоторого
при
последовательном уменьшении l С
будут мало отличаться друг от друга, начиная с некоторого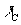 ,
соответствующего точности вычислений
e .
,
соответствующего точности вычислений
e .
Остановимся более подробно на способе решения уравнения (49). Здесь можно различить два случая: когда функция Ф(u',v') задана аналитически, то её можно найти при любых значениях (u',v'), и когда Ф(u',v') можно задать только численно в дискретной последовательности точек. Обычно в последнем случае Ф(u',v') находится в результате расчёта хода лучей через заданную оптическую систему (имеется в виду передаточная функция в геометрическом приближении) и вычисления волновых аберраций для отдельных точек выходного зрачка относительно сферы сравнения, тогда как в первом случае используются готовые формулы, выведенные теоретически для разного типа волновых аберраций. При этом вычисление в этом случае часто сводится к оценке табулированных интегралов математической физики. Такой метод решения дает достаточно точные результаты, однако вычисления для каждого частного случая задания волновых аберраций представляют значительные математические трудности.
Итак, пусть функция Ф(u',v')
известна для любых значений u',v'Î
D, тогда при заданных
(u,v) и выбранном l
C
решение (49) приближенно
можно было бы найти графически, построив график функции Ф(u',v')
- Ф(u'-u,v'-v)
и отметив точки пересечения полученной кривой с прямоугольной сеткой, полученной
соединением точек с координатами u'=±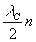 и v'=±
и v'=±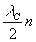 ,
где n = 1,2,3,... Однако
на практике целесообразно производить аналогичный поиск точек (u'n,v'n)
с помощью ЭВМ. Для этого надо выбрать очень малый шаг изменения D
u
и D v
и искать решения уравнения (49), как
это было предложено в работе /32/.
,
где n = 1,2,3,... Однако
на практике целесообразно производить аналогичный поиск точек (u'n,v'n)
с помощью ЭВМ. Для этого надо выбрать очень малый шаг изменения D
u
и D v
и искать решения уравнения (49), как
это было предложено в работе /32/.
Рассмотрим теперь случай, когда характер поведения функции Ф(u',v') заранее не известен. Тогда следует непосредственно решить уравнение (49). Если Ф(u',v') находится в отдельных точках с помощью расчёта хода лучей, то при этом целесообразно в программе ввести "обратную связь", т.е. создать корректирующий алгоритм, управляющий заданием направляющих косинусов на входе оптический системы в зависимости от хода изменения волновых аберраций. Для построения такого алгоритма можно воспользоваться интерполяцией функции Ф(u',v') на участке u'n-1 £
u £
u'n; v'n-1 £
v £
v'n в виде полинома, степень которого зависит от l
С. При достаточно малых l
С<<l
всегда можно считать, что
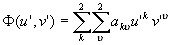
Кроме этого, для построения машинного алгоритма следует вместо решения (50) искать последовательные максимумы
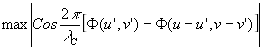
При составлении программы вычисления (37) целесообразно перейти к новой системе координат, начало которой расположено в центре области D, а оси совпадают с осями симметрии, интегрируемой области.
Наконец, при вычислении чисел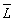 при
дискретном задании аргумента рекомендуется также изменить "квантование по уровню"
и согласовать положение расчётных точек
(um,vm)
с характером изменения функции L. Для
этого при построении управляющего алгоритма можно воспользоваться экстраполированием
L полиномами второй степени.
при
дискретном задании аргумента рекомендуется также изменить "квантование по уровню"
и согласовать положение расчётных точек
(um,vm)
с характером изменения функции L. Для
этого при построении управляющего алгоритма можно воспользоваться экстраполированием
L полиномами второй степени.
В заключение этого параграфа обратим внимание на тот факт, что сами по себе частотно-контрастные характеристики или передаточные функции не могут служить самостоятельными характеристиками качества оптических систем, ибо они не учитывают энергетические возможности оптического прибора. Кроме этого, в силу того обстоятельства, что точность расчёта этих кривых совершенно не связана с шумовыми характеристиками приемников, пока нет возможности применить к интерпретации этих кривых теорию информации. Следует ещё обратить внимание на некоторые соображения, изложенные Муратом /33/ в конце его большого обзора, посвящённого аппаратуре для измерения частотно-контрастных характеристик.
Для характеристики качества объективов совершенно недостаточно получить один или несколько частотно-контрастных характеристик при изменении нескольких параметров. В связи с этим Мурат предлагает находить передаточные функции при изменении следующих параметров: дефокусировка, полевой угол, азимутальный угол, относительная апертура, цвет* (Примерно аналогичные параметры были также положены нами в основу при классификации оптических систем /34/.). В частном случае в приведённой им таблице, когда каждый у перечисленных параметров мог, соответственно, принимать 5,5,2,5,2 дискретных значений, число различных комбинаций равно 630, соответственно столько же надо иметь и графиков передаточных функций. Очевидно, что измерить столько графиков для одного объектива практически невозможно. Что же касается выполнения аналогичных численных вычислений, то это задача уже совершенно не реальна при существующей методике вычислений. Однако принципиальная трудность состоит в том, что не существует пока способа обработки такого рода информации, а также достаточно надёжно установленных критериев качества.
6. Критерии качества оптических систем
Ранее в § 3 мы обсуждали вопросы, относящиеся к формированию изображения, при этом основное внимание было сосредоточено на волновых аберрациях и затем на выводе передаточной функции, как полезной аналогии радиоэлектронике. Однако непосредственное изучение общих закономерностей, которые имеют место в самом дифракционном изображении при аберрациях, даёт не менее ценную информацию о свойствах оптической системы. Первые исследования, относящиеся к дифракционному изображению точки в присутствии аберраций при монохроматическом освещении, были предприняты Релеем и Стрелем. Релей /35/ исследовал, какое будет изображение в фокусе цилиндрического объектива при прямоугольной апертуре и при присутствии несимметричных аберраций, а также исследовал эффекты сферических аберраций третьего порядка. При исследовании сферических aбберраций Релей сосредоточил свои усилия только на определении интенсивности в центре дифракционной картины. В результате этих исследований он сформулировал важный критерий на допуск волновых аберраций по зрачку, известный в настоящее время в обобщённой форме как предел Релея. В этом критерии утверждается, что качество оптического прибора существенно не изменится при наличии аберраций общего типа, если они таковы, что деформированный фронт волны на выходном зрачке со стороны изображений не отступает больше, чем на четверть длины волны от соответственно выбранной сферической поверхности. Стрель в своей книге /36/ и в многочисленных статьях, опубликованных главным образом между 1893 и 1930 годами изучал эффекты зейделевских аберраций, но при этом главное внимание сосредоточил на исследовании изменения интенсивности вдоль главного луча Для того, чтобы уяснить, в чём сущность этих понятий, обратимся снова к рассмотрению идеального дифракционного изображения точки.
Эйри /37/ вывел формулу для распределения освещённости света в дифракционной картине
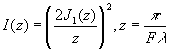 (53)
(53)
В этой формуле F - приведённое фокусное расстояние, r - расстояние от положения геометрического изображения точки. J1(r) - бесселевая функция первого рода. Значения I(z) при целочисленных значениях z=0,1,2,...6 дано в таблице на стр.87 в книге Марешаля и Франсона /5/. Первый минимум I(z) получается при z = 3.83, откуда находится первый радиус тёмного кольца в картине Эри r1 = 1.22F. Доля общей энергии, заключённая в центральном ядре, составляет 84% от всей энергии, содержащейся в картине Эри. При увеличении приведённого радиуса z. с 3.83 до 13.32 эта доля энергии увеличится на 12% (см. таблицу 3 на стр.30 в /5/* (Долю светового потока, приходящуюся на кольцо Эри, можно уменьшить посредством аподизации. Обстоятельный обзор об успехах применения аподизации в оптике и спектральных приборах написан Жакино /38/. ))
Рассмотрим теперь, что произойдёт с распределением освещённости в картине Эри при введении малых аберраций. Можно предположить, что центральный дифракционный диск из-за аберраций увеличится в размерах без значительного изменения в общей яркости. В действительности кажущийся размер диска и положение светящихся дифракционных колец остаются почти неизменными. Наряду с этим наблюдается заметное уменьшение в освещённости диска и потеря света перераспределяется по далёким дифракционным кольцам. Если объект состоит из единичной светящейся точки или двух, близко расположенных, то эффект малых аберраций практически не является существенным. Действительно, так как центральный диск для изображения точки оказывается много ярче, чем кольца, то наблюдение изображения двойной звезды оказывается почти неизменным*(* Мы не рассматриваем случай, когда интенсивность одной из составляющих звёзд много меньше другой и влияние дифракционных колец имеет существенное значение. Применение аподизации в этом случае подробно с хорошими иллюстрациями рассмотрено Жакино в приложении к книге Стронга /39/.)
и относительное положение составляющих единичных звёзд можно измерять так же, как если бы аберрации отсутствовали. Однако, ситуация резко изменяется при получении изображений протяженных объектов со сложной структурой.
Обратимся теперь снова к критерию Релея. Рассмотрим пример, когда аберрации связаны с дефокусировкой. В этом случае, как указывает Линфут /24/, при волновой аберрации в четверть длины волны интенсивность в центральном диске уменьшится больше, чем на 17% за счёт увеличения интенсивности в дифракционных кольцах без заметного изменения размеров диска или относительного распределения освещённости по диску. Такие эффекты едва ли изменят разрешающую способность оптического прибора, если объект состоит из двух светящихся точек. По-видимому, именно такую задачу о разрешении имел в виду Релей, когда предложил свой критерий. Однако увеличение интенсивности света с 16% до 33%, приходящееся на дифракционные кольца, вызывает значительные потери контрастности тончайших деталей в изображении протяженных объектов. Очевидно, что в последнем случае критерий Релея требует пересмотра.
Именно для того, чтобы учесть явление падения контрастности в изображении, Стрель предложил оценивать качество изображения по параметру, представляющему собой отношение интенсивности в центральном ядре точечно-дифракционного изображения в реальной системе к соответствующей интенсивности в дифракционном ядре в той же системе, но свободной от аберраций. Это отношение, которое мы обозначим через V, принято называть критерием Стреля. Очевидно, что, зная величину V, мы можем приближенно определить долю светового потока, приходящуюся на центральное ядро, равное 0.84V. Соответственно, доля светового потока, дифрагирующего вне ядра: d
=1-0.84V. Стрель в качестве допуска для оптических систем предложил неравенство V³
0,80.
Следует обратить внимание, что ряд авторов при теоретических выкладках безоговорочно определяют критерий Стреля как отношение освещённости в максимуме дифракционного пятна, создаваемого данным прибором, к освещённости в максимуме дифракционного пятна при отсутствии у данного прибора аберраций:
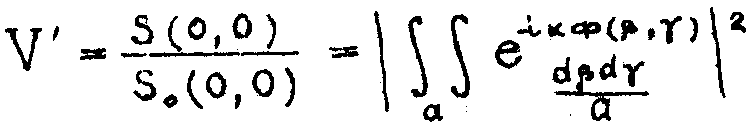 (54)
(54)
(см. по этому поводу /4/ на стр.137).
Такое определение расходится с изложенным нами выше и, кроме того, неудобно, ибо V' принципиально невозможно измерить потому, что на практике можно найти только усредненное значение освещённости. Однако при численных расчётах обычно вычисляют V'. Возможно, что во многих случаях различия между V и V' будут несущественными, но таких сравнений никто не проводил.
Дальнейшим развитием идеи Релея является работа Марешаля. который вывел допуски на аберрации в общем случае. Его исследования были основаны на соотношении между интенсивностью в точках, близких к максимуму дифракционной картины, и среднеквадратичном отклонении волнового фронта от специально выбранной сферы сравнения /5/. Марешаль показал, что если вслед за Редеем потребовать, чтобы падение интенсивности в центре дифракционного пятна не превышало 20%, то среднеквадратичное отклонение волнового фронта от сферы сравнения должно удовлетворять неравенству
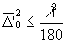 (55)
(55)
Это неравенство даёт возможность найти допуски для отдельных видов аберраций, а также в общем случае, когда имеют место дефокусировка, сферическая аберрация, кома и астигматизм.
Соответствующие формулы и оценки для аберраций мокко найти в книге Марешаля и Франсона.
Следующий важный шаг в разработке теории качества принадлежит Линфуту. В своих работах он попытался связать понятие качества, со свойствами объекта оптической системы и фотографических материалов. База для такого совместного рассмотрения была подготовлена предыдущими исследованиями. Прежде всего теория передаточных характеристик позволяет связать свойства оптической системы и фотографической эмульсии, которая фиксирует изображение. Действительно, при определённых условиях фотографическая эмульсия может также рассматриваться как фильтр пространственных частот. Тогда фотографический прибор может быть представлен с помощью двух линейных фильтров пространственных частот и результирующее пропускание будет определяться произведением обеих кривых пропускания, т.е. частотно-контрастной характеристикой или передаточной функцией.
Но этого ещё недостаточно, ибо, как было отмечено в конце предыдущего параграфа, для интерпретации самих кривых передаточных функций необходимо ввести понятие качества. В этой связи при разработке теории Линфут писал /24/, что после создания теории частотно-контрастных характеристик встал вопрос о том, какие именно свойства передаточной функции соответствуют хорошему изображению, и стало очевидным, что мы нуждаемся в средствах решения, какая из двух высококачественных фотографических систем превосходит другую и в каком смысле. Чтобы это решить, нужна была теория оценки качества изображений, приспособленная к фотографическим системам и выраженная в терминах частотно-контрастных характеристик.
Для решения поставленной задачи казалось полезным воспользоваться теорией случайных процессов и попытаться ввести понятие корреляционной функции при описании образования оптических изображений. Основой для развития своей теории Линфут выбрал рассмотрение корреляции между распределением освещённости в объекте и изображении. По этому поводу во вводной части своей книги он пишет, что если рассматривать образование изображений как наложение светящихся "ядер" Эри, то потеря в качестве изображений, следующая из уменьшения света на 20% по критерию Стреля, приводит к ослаблению корреляции между распределением интенсивности в объекте и изображении. Это следует из того, что в изображении растянутого объекта каждое светящееся ядро перекрывается системой колец от большого числа ближайших ядер. Когда V уменьшается, количество "паразитной" засветки увеличивается, и корреляция между деталями изображения и объекта становится слабее. Эта идея о корреляции между объектом и изображением, как мы увидим ниже, нашла своё отражение в качественных формулировках критериев качества, разработанных Линфутом.
7. Показатели качества оптических систем, предложенных Линфутом
Для оценки качества оптического изображения Линфут /24/ предлагает пользоваться определёнными формулами, предназначенными для количественной оценки меры подобия между объектом и изображением. При создании таких критериев возникают трудности, обусловленные тем обстоятельством, что само по себе понятие качество изображения во многом субъективно и сильно изменяется в зависимости от назначения оптической системы. В этой связи он пишет, что, по крайней мере, при интерпретации понятия качества в него вкладывают два разных смысла. Вo-первых, предполагают, что при изображении высокого качества изображение должно быть наиболее близко к оригиналу. Во-вторых, это же можно понимать и в том смысле, что при хорошем качестве мы получаем максимум, информации из изображения, подвергнув его соответствующему анализу. Во многих случаях, например, в спектроскопии изображение едва ли вообще похоже на объект. В этих системах вторая интерпретация кажется более естественной. С другой стороны, в фотографии с обычными камерными объективами первая интерпретация на первый взгляд кажется более удобной.
Однако, если стремиться глубже разобраться в роли оптической
системы и фотографической эмульсии при получении, можно считать выполнение условия
изопланарности и затем найти Ф для всей области в виде суммы по всем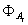 (где
Ai -
составляющая область) с соответствующими статистическими весами и дополнительной
нормировкой.
(где
Ai -
составляющая область) с соответствующими статистическими весами и дополнительной
нормировкой.
Ф и все последующие оценки можно также выразить через частотно-контрастные переходные характеристики /4, 24/.
Рассмотрим отношение вида
T=∫∫I2(x,y)dxdy / ∫∫G2(х,y)dxdy (56)
которое называется "относительный структурным содержанием". Линфут считает, что эта вторая качественная оценка предназначена для оценки способности изображения воспроизводить тонкие детали объекта.
Третья оценка качества изображения, не менее интуитивное понятие, чем первое, основана на выполнении функции взаимной корреляции между I(х,у) и G(х,y)
Q = ∫∫GIdxdy ½
∫∫G2dxdy
Из тождества
[G2 - ( - I)2] + I2 = 2
- I)2] + I2 = 2 I
I
сразу же следует, что эти три оценки не являются независимыми, а ввязаны между собой тождеством
Ф + Т = 2G
Показатели качества подобно передаточным характеристикам можно построить в форме графиков, откладывая по осям параметры, характеризующие положения плоскости изображения и аберрации. Так, например (см. рисунки на стр.104 в /4/), можно построить графики Ф, Т и G при изменении положения фокальной плоскости и при разных значениях отношения сферических аберраций третьего и пятого порядков.
В настоящее время кажется невозможным выделись какое-либо один из трёх показателей как преимущественный по отношению к другим. Линфут обобщил приведённые выше показатели качества на случай фотографических систем, при этом существенно используется представление о линейности воспроизведения интенсивности света в фотоэмульсии. При таком рассмотрении, влияние рассеяния света в слое эмульсии (т.е. диффузный ореол) может быть учтено путем образования свертки двух функций, соответствующих распределению света в оптическом изображении точки и фотографической функции размытия или же путём образования обобщённой передаточной функции, равной произведений передаточной функции самой оптической системы и фотографического коэффициента передачи контраста. Наконец, Линфут в заключении своей книги сделал попытку найти информационное содержание изображений, воспользовавшись теорией Шеннона, однако эти идеи находятся пока в самом зачаточном состоянии.
З а к л ю ч е н и е
В данном отчёте была сделана попытка обобщения наиболее важных результатов теории, которые относятся к понятию качества оптического изображения. Так как с понятием качества изображения непосредственно связываются многочисленные требования, предъявляемые к оптическому прибору, предназначенному для решения различных задач, то очевидно, что это понятие непрерывно изменяется и во многом субъективно. По мере усовершенствования как оптики, так и технологии изготовления к точности отображения объекта в изображении предъявляются всё более повышенные требования. Значительные успехи дифракционной теории аберраций дали возможность сознательно подойти к расчёту оптических систем с учётом дифракции света, а также других искажений, связанных с конечностью длины волны.
Следует обратить особое внимание на трудности теории, когда оптическая система анализируется в отрыве от свойств приемников радиации, в частности, от шумовых характеристик фотоэмульсий.
- 130 -
Никакие передаточные характеристики или другие критерии качества в принципе не могут быть признаны удовлетворительными, если они не учитывают энергию излучения источника и свойств приемников этого излучения. В частности, существенным недостатком всей теории передаточных характеристик является исключение ради нормировки факторов, определяющих светосилу оптической системы. В результате на основе этой теории можно методами последовательных коррекций получить почти идеальную оптическую систему, которая не будет пропускать свет.
В этой связи представляет несомненно большой интерес работа Л.А.Хальфина, посвящённая информационно-статистической теории оптических систем и оценке их качества. В этой теории с самого начала оптический прибор рассматривается на основе применения общей статистической теории случайных процессов к интерпретации результатов наблюдений. В своих лекциях, прочитанных в 1965 году в Государственном Оптическом институте, Л.А.Хальфин показал, что при рассмотрении множества возможных оптических сигналов от объекта можно воспользоваться неравенством Рау-Крамера из математической статистики и вывести выражение для нижней сценки дисперсии наблюдаемого параметра, если задачу о получении информации об объекте по изображению рассматривать как параметрическую задачу в статистической теории обнаружения сигналов. Такое значение дисперсии предлагается рассматривать как критерий качества оптического изображения, при этом понятие качества связывается с оптимальным методом обработки результатов наблюдений. Существенно, что при применении этого критерия к конкретным задачам интенсивность источника света, светосила системы, передаточная характеристика и дисперсия шума приемника оказались связаны одной формулой. К сожалению, для практической реализации этой теории требуется проводить большое число трудоемких вычислений, которые можно осуществись только на ЦВМ и при получении большого штата опытных программистов. Видимо, поэтому прикладные вопросы теории пока мало разработаны и ждут своего решения.
- 131 -
Однако с уверенностью можно оказать, что дальнейшее развитие теории качества изображения сейчас немыслимо без учета статистических свойств как оптического прибора, так и света.
- 132 -
Л и т е р а т у р а
1. В.С.Игнатовский. Труды ГОИ, вып.6, стр.30 (1920).
2. В.А.Фок. Труды ГОИ, вып.27, стр.1, 1924.
3. А.Земмерфельд. Оптика, гл.5, ИЛ (1953).
4. 0'Нейл. Введение в статистическую оптику, изд. "Мир", 1966.
5. А.Марешаль, М.Франсон. Структура оптического изображения, изд. "Мир", 1964.
6. Crozl, Dormois, Durand. Compt.Rend., 228, 824 (1949).
7. J.Robieux. These, Paris, 1959, Annales de Radioelect., 14, 57, 187 (1959).
8. M.Born, E.Wolf. Principles of Optics, 3rd. Ed. Pergamon Pr ss, 1965.
9. Современная математика для инженеров, изд. МЛ, М., 1958.
10. Д.Строук. Введение в когерентную оптику и голографию, изд. "Мир", 1967.
11. L.Mertz. "Transformations in optics". (русское изд.: Л.Мерц, Интегральные преобразования в оптике, изд. "Мир", 1968).
12. K.Miamoto. Progress in Optics, 1, 41 (1961).
13. Picht. Arn. Rhys., Lpz., 80, 491 (1926).
14. Steward. Trans. Camb. Phil. Soe, 23, 235 (1926).
15. B.R.A.Nijboer. Physica, 10, 679 (1943); 13, 605 (1947).
16. F.Zernike, B.R.A.Nijboer. La theorie des images optignes, Paris, p.227, 1949.
17. E.Wolf. Rер.on Progr.in Optics, 14, 95 (1951).
18. K.Nienhnis, B.R.A.Nijboer. Physica, 14, 599 (1949).
19. H.Linfpof. "Recent Advances in Optics", Clarendon Press, 1955.
20. A.Marechal. Rev. Opt., 27, 73 (1948).
21. N.G.Van Kampen. Physica, 14, 575 (1949).
22. P.M.Duffienx. L'lntegrale de Fourier et ses Applications á 1'Optique (Rennes, 1946).
- 133 -
23. P.Dumontet. Optica Acta, 2, 53 (1955).
24. E.H.Llnfoot. "Fonrirer methods in Optical Image Evaluation", The Focal Press, L. and H.Y., 1964.
25. Е.Abbe. Archiv f. Microscopische Anal., 9, 413 (1873).
26. H.H.Hopkins. Proc.Roy.Soc., A217, 408 (1953).
27. О.Шаде. Оценка качества оптического изображения. Сб. статей, изд. геодезич. лит-ры, стр.5, 1959.
28. H.H.Hopkins. Proc.Roy.Soc., B62, 22 (1949).
29. Linfoot. Ргос.Rоу.Soc., А239, 522 (1957).
30. De.M., Ргос.Rоу.Sос., А233, 96 (1955).
31. Б.А.Киселев, П.Ф.Паршин. Прикладная спектроскопия, 2, 212, 1965.
32. П.Ф.Паршин. Прикладная спектроскопия, 1, 264, 1964.
33. K.Murata. Progress on Optics, 5, p.200, 1966.
34. Г.Г.Слюсарев, П.Ф.Паршин. ОМП, № 8, 1967.
35. Lord Rayleigh. Phil.Mag. 5, 8, (1879).
36. K.Strehl. Therie des Fernrohrs, Leipzig, 1894.
37. G.B.Airy. Trans.Camb.Soc., 5, 289 (1835).
38. P.Jacquinot. Progress in Optics, vol.3, p.5, 1964.
39. D.Strong. Concepts of Classical Optics", Washington, 1956.

