|
|
 |
 |

|
| |
ШУМЫ В МЕТОДЕ ФУРЬЕ-СПЕКТРОМЕТРИИ
§ 15. Дисперсия шума в спектрограмме
Как уже было указано в § 6, в общем случае в спектр будет преобразовываться не G*(t), а E(t)=G*(t)+x
(t), где второй член есть случайная функция шума. Шум в спектрограмме найдём как
У(w )
= 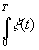 Cosw
tdt (59) Cosw
tdt (59)
если принять, что спектр находится в результате косинусного преобразования Фурье.
В работах /85,87/ было показано, что дисперсия шума, определяемая как математическое ожидание случайной величины у(w
), представима в виде
и 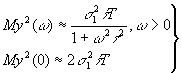 (60) (60)
где 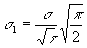 с точностью до множителя
с точностью до множителя 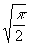 соответствует
с.к.о. в интерферограмме. На основе (60) с.к.о. в спектрограмме s
w найдем как соответствует
с.к.о. в интерферограмме. На основе (60) с.к.о. в спектрограмме s
w найдем как
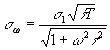 (61) (61)
В работе /116/ показано, что при применении треугольной аподизации в первой и второй степени с.к.о., соответственно, равна
s
w
(1)=0,816s
w
и s
w
(2)=0,63s
w
- 203 -
При дискретном преобразовании Фурье и вычислении интегралов по формуле (18)
s
w
'=p(z)s
w
(62)
где
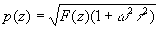
и
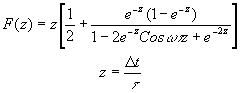
Нетрудно убедиться, что 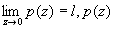 выражает зависимость уровня шума в спектрограмме от числа отсчетов, снимаемых
с интерферограммы. Этот вопрос исследовался Ж.Конн /61,115/, а также Паршиным
/85/.
выражает зависимость уровня шума в спектрограмме от числа отсчетов, снимаемых
с интерферограммы. Этот вопрос исследовался Ж.Конн /61,115/, а также Паршиным
/85/.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

