Рассмотрим снова выражение для светового потока (1). В этой формуле второй член представляет собой переменную часть интерферограммы, обозначим его через

J₀(d ) = E₀(d ) - ½E₀(0)=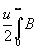(u )Cos2p u d du (25)

В соответствии с формулами (22) J₀(d ) можно рассматривать как результат применения косинусного преобразования Фурье к функции 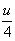В(u ), а следовательно, зная J₀(d ), можно восстановить спектр:

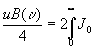
(d )Cos2p u d du (26)

В этой формуле левая часть по размерности представляет собой спектральную плотность потока излучения. Таким образом, мы нашли, что в случае идеальной приёмно-регистрирующей системы и при наличии бесконечной записи интерферограммы исходный спектр можно найти, непосредственно подвергая J₀(d ) преобразованию Фурье.

Вспомним, что применение преобразования Фурье к u (d ) - кривой видимости в случае симметричных полос - также даёт исходный спектр.

Впервые идея применения преобразования Фурье непосредственно к самой интерферограмме была высказана в 1951 году Фелжеттом /78, 83/ 2). Он же указал и на преимущества такого метода,

2) Как уже было отмечено в § I, все изложение метода Фурье-спектрометрии ведётся без привлечения более общей теории частичной когерентности. Однако ещё Фелжетт /78/ обратил внимание на тот факт, что (25) можно в общем случае рассматривать как корреляционную функцию. Примечательно, что Винер /80/ при общем описании корреляционных методов также указывает на интерферометр Майкельсона как на простейший способ получения корреляции в оптике. Исходя из этой точки зрения, интерферометр Майкельсона следует рассматривать как автокоррелятор. В трудах Бартлинга /79/ проведена работа по переводу основных терминов и формул метода Фурье-спектрометрии на язык общей теории.