Преобразование Фурье
В целях удобства дальнейшего изложения материала в этом параграфе даётся сводка некоторых основных формул, относящихся к теории преобразований Фурье с краткими пояснениями.
Ряд Фурье
Если непрерывная ограниченная функция ¦
(t) задана на интервале [-Т,Т], то её можно разложить в тригонометрический ряд Фурье по косинусам и синусам кратных дуг:
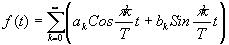 (16)
(16)
- 145 -
где
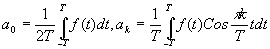
и
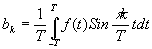 (17)
(17)
Из формул
(17) следует, что если ¦
(t) чётная функция, т.е. ¦
(-t) = = ¦
(t), то bk=0 и ¦
(t) разлагаются в ряд только по косинусам. Если ¦
(t} - нечётная функция, т.е. ¦
(-t) ¹
¦
(t), то все ak=0 и ряд (16) содержат только синусы.
Комплексная форма ряда Фурье
Воспользуемся известным тожеством Эйлера, связывающим тригонометрические функции с показательной:
еij
= Cos
j
+ iSin
j
.
После несложных преобразований
(16) можно привести к следующему комплексному представлению:
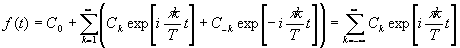 (18)
(18)
где введены следующие обозначения:
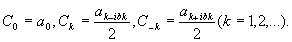 (19)
(19)
- 146 -
Интегральное преобразование Фурье
Принимая во внимание формулы (17) и (19), найдём, что
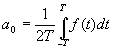
и 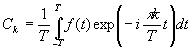 (20)
(20)
Введем обозначения
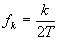 и
и 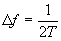 ,
и затем подставим (20) в
(18), тогда
,
и затем подставим (20) в
(18), тогда
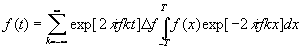
Если в этом выражении
Т→¥
, то при предельном переходе в результате замены ряда на интеграл найдём
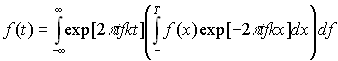
Последнее в более привычной форме можно записать в виде
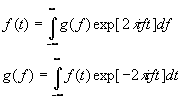 (21)
(21)
Функцию
¦
(t) части называют временным представлением процесса, a g(¦
) - ее частотным откликом. Вместо переменной ¦
часто рассматривают круговую частоту w
=2p
¦
, тогда (21) можно преобразовать к виду:
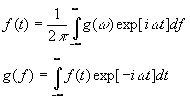
(21а)
- 147 -
Таким образом, мы показали, что разложение функции в интеграл Фурье вытекает как предельный случай разложения в ряд Фурье при неограниченном расширении области существования функции.
Проводя аналогию между обоими этими представлениями, мы видим,
что
g(¦
) есть непрерывный спектр частот, в то
время как коэффициенты Ск
можно рассматривать как дискретный спектр частот, смещённых между собой на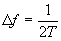 .
.
В символической записи
(21) можно записать в виде:
¦
(t) = T[g(¦
)], a g(¦
) = T*[¦
(t)]
или просто
¦
= T[g] и g = T*[¦
]
Отметим практически полезный Случай, когда ¦
(t) - четная, тогда вместо (21) имеет место косинусное преобразование Фурье:
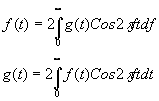 (22)
(22)
В операторной форме
(22) можно переписать в виде: a(¦
)=TC[¦
(t)]. Аналогично можно вывести выражения для синусного преобразования Фурье.
Теорема Парсеваля
Если
¦
(t)=¦
1(t)¦
2(t), то нетрудно доказать, что спектральная функция
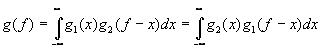 (23)
(23)
- 148 -
В операторной форме:
g(¦ ) = g1(x)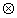 g2(x)
g2(x)
или
T[¦ 1¦
2] = T[¦ 1]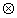 T[¦
2]
T[¦
2]
Выражение
(23) и его операторный эквивалент принято называть интегралом свертки.
Найдём теперь выражение теоремы Парсеваля в случае косинусного преобразования Фурье.
В этом случае
¦
1(-t) = ¦
1(t)
¦
2(-t) = ¦
2(t)
а следовательно, это условие выполняется также для
g1(t) и g2(t). Перейдём в правой части уравнения (23) к интегрированию в пределах [0,¥
], тогда
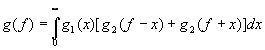 (24)
(24)
Дельта-Функция Дирака
Во многих практических приложениях часто прибегают к моделированию физического процесса в форме d
-функции Дирака. Рассмотрим два возможных её представления.
а) Если g(¦
)=d
(¦
-¦
0), то
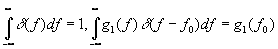
Иногда вместо интегральных свойств полезно пользоваться приближенными представлениями: d
(0)=¥
и d
(¦
)=0 при всех ¦
¹
0.
- 149 -
Для физического понимания все эти определения близки по смыслу и соответствуют модели бесконечно узкой спектральной линии с интенсивностью в центре, стремящейся к бесконечности таким образом, чтобы интегральная интенсивность стремилась к конечной величине.
Найдём временное представление d
-функции. Для этого подставим
g(¦
)=d
(¦
-¦
0) в верхний интеграл из (21):
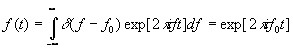
Таким образом, мы нашли, что
g(¦
)=d
(¦
-¦
0), заданной на (-¥
,¥
) соответствует комплексная временная функция.
б) Рассмотрим теперь случай, когда
d
-функция задана на правой вещественной полуоси [0,¥
], т.е.
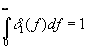
и 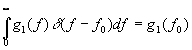
Этот случай имеет больше физического смысла, ибо можно эту модель рассматривать как приближение к узкой спектральной линии; в данном случае мы как бы учитываем, что спектр может иметь физический смысл только для положительных частот.
Аналогичный образом найдем в случае применения косинусного преобразования Фурье
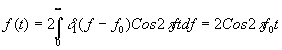
Нетрудно убедиться, что между обоими
d
-функциями существует связь:
d
1(¦
-¦
0) = d
(¦
-¦
0) + d
(¦
+¦
0)

