|
|
 |
 |

|
| |
Модель дисперсионной кривой
Выражения для аппаратных функций, подученные в предыдущих двух параграфах, можно рассматривать как результат применения модели спектра в виде d
-функции Дирака.
Эта модель имеет два существенных недостатка. Так, в силу того обстоятельства, что
F
(w
) = F
T(w
)+D
F
(w
) (12)
где
D F
(w ) º 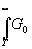 (t)Cosw
tdt (t)Cosw
tdt (13)
искажения в спектре, связанные с отбрасыванием D
F
(w
) (12), зависят от поведения G0(t) вне интервала [0,Т]. К сожалению, модель d
-функции не дает возможности оценить величину D
F
(w
). Во всяком случае из физики явления очевидно, что с увеличением разности хода погрешность D
F
(w
) должна стремиться к нулю, в то время как из данной модели следует, что D
F
(w
) неопределённа, ибо F
(w
0)=¥
, а F
Т(w
0) - конечна. Второй недостаток возникает из-за бесконечно узкой ширины линии, в результате чего форма линии не изменяется в зависимости от (D
w
)0. Однако на практике всякая спектральная линия имеет конечную собственную ширину, и при неограниченном уменьшении (D
w
)0 мы доданы получить контур спектральной линии.
Более того, в инфракрасной области часто приходится иметь дело с широкими полосами сплошного спектра, и в этом случае модель
- 179 -
d
-функции уже не отвечает практическим требованиям.
В связи с этим в работе Киселёва и Паршина /93/ была рассмотрена модель спектра, представленного в виде
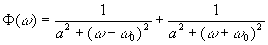 (14) (14)
Главное достоинство этой модели состояло в том, что, изменяя
собственную полуширину F (w
), равную 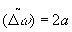 ,
можно было исследовать закономерности в Фурье-спектрометрии при переходе от
узкой линии до широкой полосы. ,
можно было исследовать закономерности в Фурье-спектрометрии при переходе от
узкой линии до широкой полосы.
После подстановки (14) в (2) и выполнения интегрирования
F T(w
) = F '(w 0)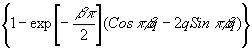 (15)
где
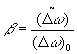
и 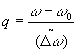
В (15) через F
'(w
) обозначен первый член в (14). Формула (15) сразу se нам даёт возможность найти значение интенсивности в центре спектральной линии:
F T(w
0) = F '(w
0)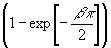 (16)
Отсюда относительное изменение интенсивности
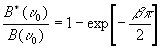 (17) (17)
Если 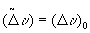 ,
то ,
то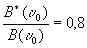 . .
На рис.5 приведены кривые B(u
) и В*( u
) для этого случая. Откуда, в частности, видно, что спектрограмма не содержит отрицательных интенсивностей и применение аподизации не требуется. Этим результатом воспользовался Т.Ричард с сотрудниками /54/ при получении спектров паров HCl и DCl. В их опытах ширина вращательных линий указанных молекул была сравнима с (D
u
)0, поэтому они не применяли аподизацию, и, несмотря на это, их спектры не содержат отрицательных интенсивностей.
- 180 -
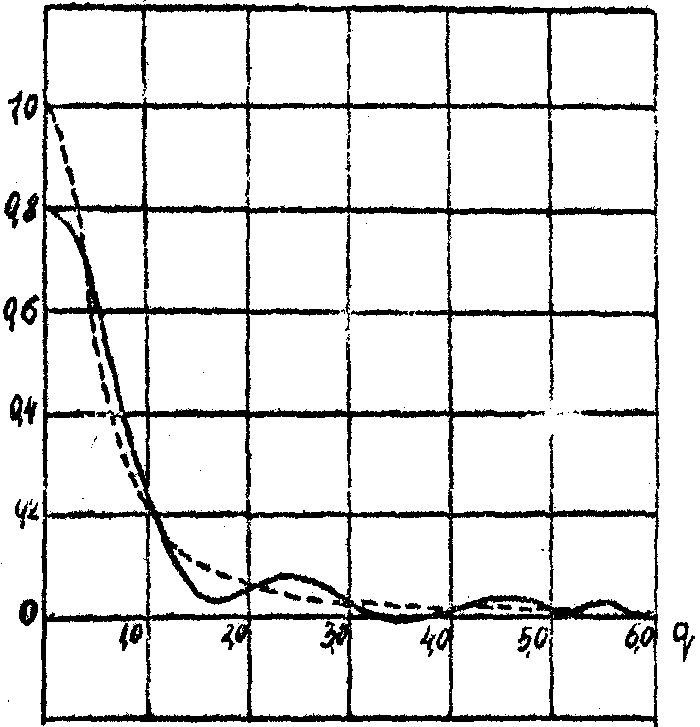
Рис.3. Сравнение нормированной дисперсионной кривой
и её спектрограммы. 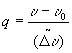
§ 10. Дискретное _преобразование Фурье
При практической реализации метода Фурье-спектрометрии приходится приближенно вычислять интегралы типа (1).
Рассмотрим вычисления (1) по формуле прямоугольников*:
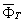 (w
) = 2D t (w
) = 2D t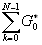 (D
tk)Cosw D tk
(18) (D
tk)Cosw D tk
(18)
* При анализе 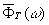 целесообразно
рассматривать правую часть формулы (18}
не как приближённее вычисление (1), а
как действие нового линейного оператора
SN
на
¦ (t)
при этом целесообразно
рассматривать правую часть формулы (18}
не как приближённее вычисление (1), а
как действие нового линейного оператора
SN
на
¦ (t)
при этом
SN¦ (t) = 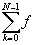 (D
tk)Cosw D tk (D
tk)Cosw D tk
- 1^1 -
После подстановки (28) в (18) и замены порядка суммирования и интегрирования
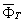
(w
) = 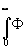 (х)WN(w
-x)dx (19) (х)WN(w
-x)dx (19)
где
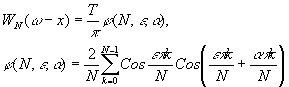
(20)
Здесь X = w
c+e
(p
/T), w
= Х+a
(p
/T) и через w
c обозначена частота, связанная с N соотношением:
w
c = N(p
/T)(2n+1) , где n - целое число.
В (19) WN(w
-w
0) есть аппаратная функция при дискретном интегрировании. Полагая F
(x)=d
1(x-w
0), мы найдём, что
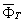
(w
) = WN(w -x)
В этом случае физический смысл параметров e
и a
становится очевиден:
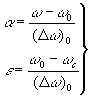 (21) (21)
и w
c = N(2n+1)( D
w
) 0. То есть a
и e
суть спектральные интервалы, выраженные в единицах (D
w
)0; w
c есть такая частота, для которой разрешавшая способность
Rc = 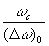 = N(2n+1)
= N(2n+1)
- 182 -
В (20) через j
(N,e
,a
) обозначена аппаратная функция, нормированная на единице. После выполнения суммирования в (20)
j (N,e
,a ) =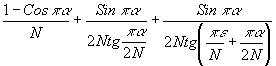 (22)
Свойства j
(N,e
,a
)
1. Периодичность:
j
(N,e
,a
+2Nk) = j
(N,e
,a
)
2. Зеркальная симметрия:
j
(N,e
-2e
-a
) = j
(N,e
,a
)
Откуда спектр на частоте w
0 = w
C ±
e
( D
w
) 0 имеет своё отображение на частоте w
' = w
C ±
e
(D
w
)0, то есть w
'-w
C = w
0-w
C.
3. Из предыдущих свойств следует, что методу Фурье-спектрометрии свойственно наличие свободного спектрального интервала
(D
w
)' = N(D
w
)0
Эти свойства иллюстрирует рис .4.
При n=0 w
C = N( D
w
) 0 и (D
w
)' = w
C
Рассмотрим теперь, как часто будут расположены точки на интерферограмме, если w
0 = w
С.
В этом случае N=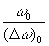 ,
но ,
но 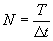 откуда
откуда
D
t=p
/w
0
Для монохроматической линии
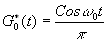
и 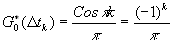
- 183 -
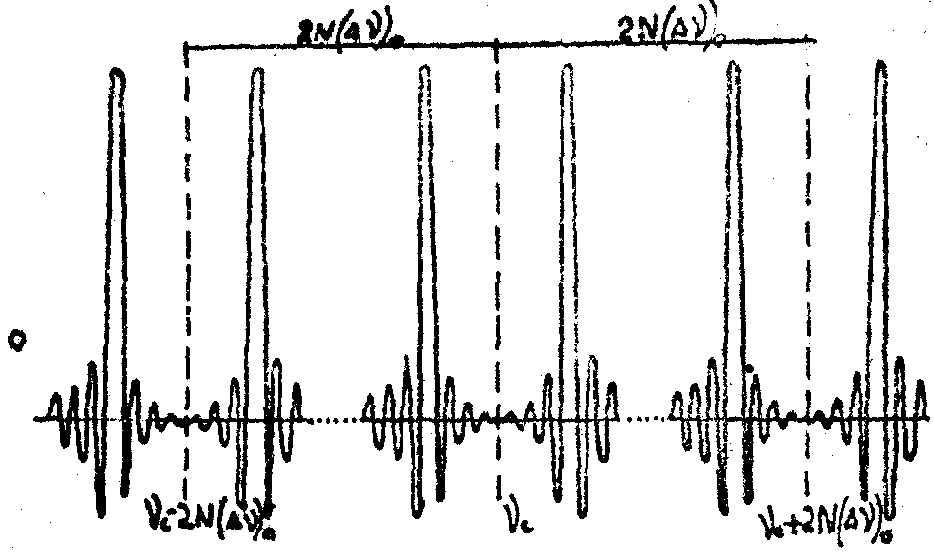
Рис.4а. Аппаратная функция Фурье-спектрометра при дискретном преобразовании Фурье.
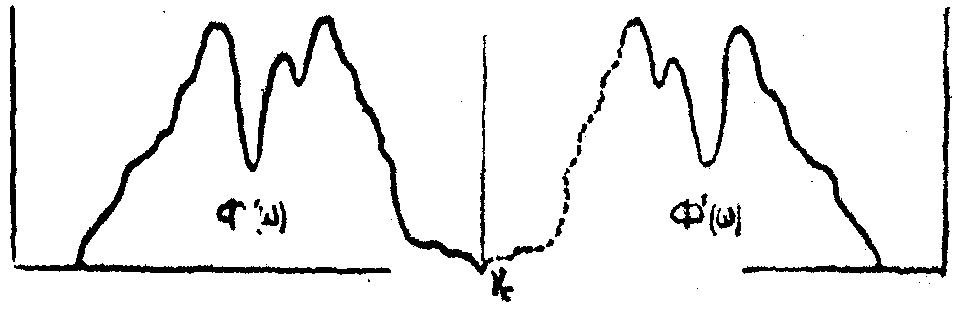
Рис.4б. Спектрограмма при дискретном преобразовании Фурье (реальный спектр и его зеркальное изображение).
- 184 -
Таким образом, мы нашли, что при таком выборе N точки на интерферограмме будут отстоять друг от друга на D
d
=2vD
t=l
0/2 и все они будут принадлежать огибающей интерферограммы (кривой видимости).
Вели же мы теперь примем, что n¹
0 , то при w
0 = w
С имеем
D
t = (2n+1)p
/w
C и D
d
= (l
0n+l
0/2)
В этом случае точки на интерферограмме по-прежнему будут принадлежать её огибающей, однако с пропуском одного, двух и т.д. полос в интерферограмме между точками. Этот результат, если позволяет отношение сигнал к шуму, даёт возможность значительно сократить объём вычислений, ибо форма аппаратной функции слабо зависит от N. Более подробные сведения по этому вопросу можно найти в работе /94/. Если w
С рассматривать как предельную частоту в спектре, то на основе теоремы Котельникова свойства аппаратной функции имеют простую интерпретацию.
Именно такой подход был развит в работе Ж.Конн /61/ (см. по этому поводу также /94/). В диссертации Петрова /33/, кроме прямоугольной квадратуры, выведены аппаратные функции в случае вычисления по формуле Симпсона и по методу Филона.
Остановимся теперь на вопросах проведения численных вычислений
спектральных кривых. Обратимся снова к формуле
(18) и вспомним, что F
(w )=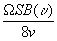 ,
тогда
(18) можно преобразовать к виду: ,
тогда
(18) можно преобразовать к виду:
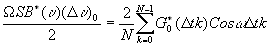 (23) (23)
Для дальнейшего преобразования (23) заметим, что из (21) следует, что u
=(N-e
+a
)(D
u
)0 и w
=(N-e
+a
)p
/T. В результате
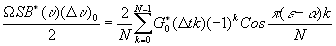 (24) (24)
- 185 -
Выражение (24) можно рассматривать как исходное для проведения численных вычислений. Рассмотрим случай, когда спектрограмма вычисляется в равноотстоящих точках.
Предположим, что нас интересует участок спектра [u
1,u
2] и мы хотим на этом участке вычислить М значений спектрального светового потока при вычислении по N отсчётам с интерферограммы. Тогда e
=N-R1 и a
должна принимать значения
a
= (R1+R2-N)m/M (m = 0,1,2, ...,M)
где R1 = u
1/(D
u
)0 и R2 = u
2/(D
u
)0 суть разрешающие способности.
Однако проводить вычисления в равноотстоящих точках требует большого машинного времени, поэтому представляется целесообразным усовершенствовать программу автоматического расчёта, вводя квадратичную экстраполяцию. При такой программе число точек на любом участке спектральной кривой будет изменяться в зависимости от поведения спектральной функции /95/. Если мы хотим вычислить спектрограмму с применением аподизирующей функции ¦
(t)=1-ï
tï
/T вместо (24) спектральные крив: в надо вычислить по формуле:
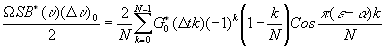 (25) (25)
В работе Формана /96/ предлагается другой алгоритм вычислений, который, до заявлению автора, более эффективен*. Кроме этого, в настоящее время разрабатываются специализированные ЦВМ для выполнения преобразования Фурье. Одно из таких устройств, созданное большой группой японских учёных и конструкторов /119/, работает совместно с интерферометром в единой системе, то есть вся система в целом представляет собой действительно Фурье-спектрометр. Аналогичное устройство описано Хаффманом и Ванассом /97/.
* Теперь при вычислениях с N > 1000 обычно пользуются алгоритмом быстрого преобразования Фурье.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

