|
|
 |
 |

|
| |
Искажения в приемно-регистрирующем тракте
В § 4 было выведено выражение (27) для интерференционной модуляции светового потока и электрического напряжения в цепи, получаемого после приемника.
Теперь мы рассмотрим прохождение электрического сигнала через приёмно-усилительный тракт, причём ограничимся приближением одного электрического фильтра, представленного в виде RC-цепочки; при этом будем считать, что напряжение снимается о конденсатора. Пусть к четырёхполюснику, состоящему ив активного сопротивления R и емкости С, приложено переменное напряжение e
(t) Тогда в контуре возникнет ток i на активном сопротивлении R, а на конденсаторе возникнет ток смещения. Обозначим через u напряжение на обкладках конденсатора. Уравнение цепи имеет вид:
iR + u = e
(t)
Так как ток проводимости i должен быть равен току смещения, то, обозначая через q, величину заряда на обкладках конденсатора, найдём, что
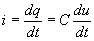
С учётом последнего уравнение цепи можно представить в виде
t 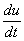 + u = e (t)
+ u = e (t) (31)
где t
=RC.
Для решения уравнения (31) зададим e
(t) = Ф(w
)dw
Cosw
t и положим u(0)=0. Тогда решение (31) найдём в виде
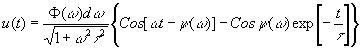 (32) (32)
где y
(w
)=arctgw
t. В общем случае, учитывая (28), u(t) найдём как интеграл
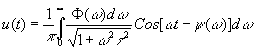 (33) (33)
При выводе (33) в формуле (32) был отброшен второй член, который важен при рассмотрении "переходных" процессов. Однако, возможно, что при прерывном (шаговом) методе регистрации интерферограмм такое приближение уже недостаточно.
В ряде случаев u(t) удобно представить в виде 14)
14) Шеннон /84/ показал, что уравнение (34) в общем случае возникает как результат воздействия на сигнал G*0(t) линейного фильтра. Если с некоторым запаздыванием u(t) пропустить через "обратный" фильтр, то можно восстановить G*0(t).
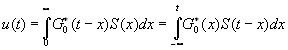 (34) (34)
где
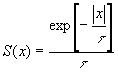
Общие выводы о воздействии электрического фильтра на G*0(t) непосредственно следуют из рассмотрения (33). Прежде всего мы замечаем, что положение максимума u(t) смещается относительно t=0 (нулевой разности хода) из-за возникновения фазовых смещений y
(0). Кроме этого, возникнет асимметрия интерферограммы относительно нового максимума.
При регистрации интерферограмм для правильного выбора
t удобно
использовать представления о предельной длине волны l
0= 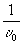 в спектре B(u
). Откуда сразу можно вычислить
w 0
в спектре B(u
). Откуда сразу можно вычислить
w 0=4 p
v u 0
и, положив w
0t =1 ,
найти t
15).
В первом приближении тогда можно принять, что максимум
u(t) сместится в точку
t=t .
Фазовую поправку
t(w )=arctgw
1t ,
для разных w
, как это было предложено Ж.Конн
/61/, можно учесть при численном выполнении
преобразования Фурье.
Наконец, заметим, что при применении моделей спектра для Ф(w
) можно более полно оценить искажения, вносимые электрическим фильтром. Для этого надо вычислить интеграл (33). Такие вычисления для дисперсионной кривой приведены в /85/.
Выше мы рассматривали только фазовые искажения, вносимые фазовой
характеристикой электрического фильтра. Искажения, вызванные частотной характеристикой
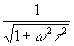 в (33), не
рассматривались, ибо
фазовые искажения, несомненно, играют в Фурье-спектрометрии более важную роль.
Кроме этого, если малы фазовые искажения за счет выбора
в (33), не
рассматривались, ибо
фазовые искажения, несомненно, играют в Фурье-спектрометрии более важную роль.
Кроме этого, если малы фазовые искажения за счет выбора 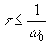 ,
то можно принять ,
то можно принять 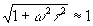 . .
15) можно вместо t
определять скорость движения зеркала
v, считая t
фиксированной: 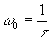 ,
но w 0 ,
но w 0=4 p
v u 0,
отсюда 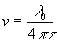
В этом параграфе мы столкнулись с проблемой выбора полосы пропускания электрического фильтра. Аналогичная проблема возникает и в классических спектральных приборах. Так, в обзоре Дмитриевского, Непорента и Никитина /86/ выбор скорости сканирования в спектрометрах при заданном t
рассматривался с точки зрения искажения для Гауссовой модели спектра. Такое рассмотрение можно было бы провести также на основе введения понятия модуляционных пространственных частот. Тогда аналогия классической спектроскопии с интерференционными методами была бы более полной.
Однако приведённое рассмотрение касалось только одной стороны задачи о правильном выборе режима регистрации при записи интерферограмм без учёта роли шумов.
На самом деле выбор t
непосредственно сказывается на уровне шумов в интерферограмме и поэтому не может быть произвольным.
Найдём связь дисперсии шума в интерферограмме с t
.
Предположим, что при регистрации приёмник является генератором белого шума и, следовательно, переменное напряжение на выходе приёмника определяется E(t) = G0(t) + x
(t). Тогда в силу соотношений (34) и (35)
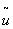 (t) = u(t)
+ h (t) (t) = u(t)
+ h (t)
(36)
где
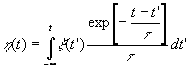 (37) (37)
Пусть дисперсия белого шума x
(t), определяемая через математическое ожидание x
2(t) , равна
Мx
2(t) = s
2
Тогда, применяя методику вычислений, разработанную в /87/, найдём, что корреляционная функция для h
(t), определяемая как математическое ожидание произведения h
(t1)×
h
(t2), имеет вид:
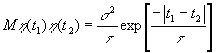 (38) (38)
а дисперсия
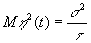
Применяя преобразование Фурье к (38), можно вычислить спектральную плотность мощности шум S(w
), которая имеет вид:
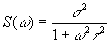
Среднеквадратичная ошибка (с.к.о.) в интерферограмме равна
C.к.о.h (t)=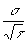 (59) (59)
Откуда следует, что для уменьшения уровня шума в интерферограмме следует увеличивать t
. Но увеличивая t
, мы вступаем в противоречие с ранее выведенным условием, соблюдение которого необходимо для правильного воспроизведения полезного сигнала G*0(t).
В методе "гетеродинной спектроскопии", предложенном Мертцем /29, 62/ и затем практически реализованным Ж.Конн /61/ (см.рис.2 и конец предыдущего параграфа), удаётся несколько увеличить t
, не искажая полезный сигнал за счёт более строгого учёта того обстоятельства, что спектр B(u
) отличен от нуля только в области (u
1,u
0) 16). В этом методе при выборе t
достаточно потребовать, чтобы,
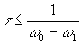
16) Более критический анализ методики, применённой Ж.Конн /61/
показывает, что после гетеродинирования
G*0(t)
посредством умножения на Cos(2p
¦ 0t+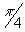 )
к новой интерферограмме уже нельзя применять только косинусное преобразование
Фурье из-за нарушения симметрии относительно
t=0. )
к новой интерферограмме уже нельзя применять только косинусное преобразование
Фурье из-за нарушения симметрии относительно
t=0.
В результате с.к.о. шума в интерферограмме уменьшится 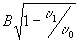 раз.
При регистрации спектра германия (рис.2) в работа Ж.Конн u
1
= 5600 см-1
и u 0
= 6100 см-1,
откуда раз.
При регистрации спектра германия (рис.2) в работа Ж.Конн u
1
= 5600 см-1
и u 0
= 6100 см-1,
откуда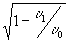 =
0, 27. =
0, 27.
Более полное решение задачи о выборе режима регистрации (определить u
и t
) возможно при рассмотрении отношения сигнал к шуму в спектрограмме.
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

