ИНТЕРФЕРЕНЦИОННАЯ МОДУЛЯЦИИ СВЕТА
Работы Майкельсона по применению интерференции в спектроскопии
Как это ни странно на первый взгляд, но работы по спектроскопии Майкельсон начал с исследований по астрономии. На основе теории колебаний Майкельсон разработал теорию интерферометра, предназначенного для изучения звёздных туманностей и двойных звёзд. Он предложил усовершенствовать метод наблюдения далёких звёзд, соединив телескоп с двухлучевым интерферометром и наблюдая с помощью такого прибора вместо изображения объекта изменение "видимости" (контрастности) интерференционной картины при изменении разности хода между интерферирующими лучами. В таком методе наблюдения истинная форма объекта косвенным образом проявляется в характере распределения интенсивности в кривой видимости. Чтобы это распределение найти, необходимо сделать дополнительно предположения о виде функции распределения энергии излучения в объекте с точностью до численных значений параметров, характеризующих эту функцию. В связи с этим Майкельсон писал, что во многих практических случаях можно предположить, что форма источника - круглый диск и единственную задачу, которую надо решить - это измерить его диаметр. Решение задачи в этом методе сводится к нахождению параметров функции с помощью математического подбора удачной функции видимости для заданной экспериментальной кривой. Произведённые им оценки показали, что главное преимущество метода - увеличение дальности в обнаружении источника от 10 до 15 раз по сравнению с телескопическими наблюдениями /8/.
В 1891 году в следующей статье Майкельсон разработал основы интерференционного спектрального анализа, относящиеся уже к задачам не астрономии, а эмиссионного спектрального анализа. Однако, по существу, эта статья явилась естественным продолжением предыдущей, как об этом можно судить по следующему высказыванию автора: "Было показано, что посредством интерпретации "кривой видимости" форма распределения света может быть точно выведена, даже когда объект находится за пределами разрешающей силы телескопа". В настоящей статье предполагается показать, что те же принципы имеют место в спектроскопических наблюдениях и даже с большей силой. Действительно, спектральная линия может быть рассмотрена в телескоп..., и "линия" могла бы быть изучена точно тем же способом, как небесная звезда /9, 10/.
При таком анализе определение распределения энергии в контуре спектральной линии непосредственно зависит от способа интерпретации кривой видимости. Для изучения формы спектральных линий Майкельсоном быв предложен двухлучевой интерферометр (рис.1). При движении каретки с зеркалом ¦
возникает изменение разности хода d
между интерферирующими лучами или эквивалентное изменение толщины воздушной пластинки, образованной зеркалом ¦
и изображением зеркала g'. Интерференционные полосы или кольца, наблюдаемые через зрительную трубку h, при перемещении каретки также движутся, и освещённость в любой точке интерференционной картины при этом изменяется. Майкельсон теоретически вывел характер изменения освещённости в центральной точке интерференционной картины в зависимости от свойств источника света. Он показал, что в случае монохроматического источника освещённость будет меняться по гармоническому закону и в случав неоднородного - изменение можно описать с помощью интегралов Фурье, причём в последнем случае величина этой освещённости или изменения разности хода, начиная от d
=0, будет быстро падать и тем скорее, чем шире спектральная полоса источника.
Зарегистрировать все детали кривой изменения освещенности при изменении d
практически достижимо только при применении
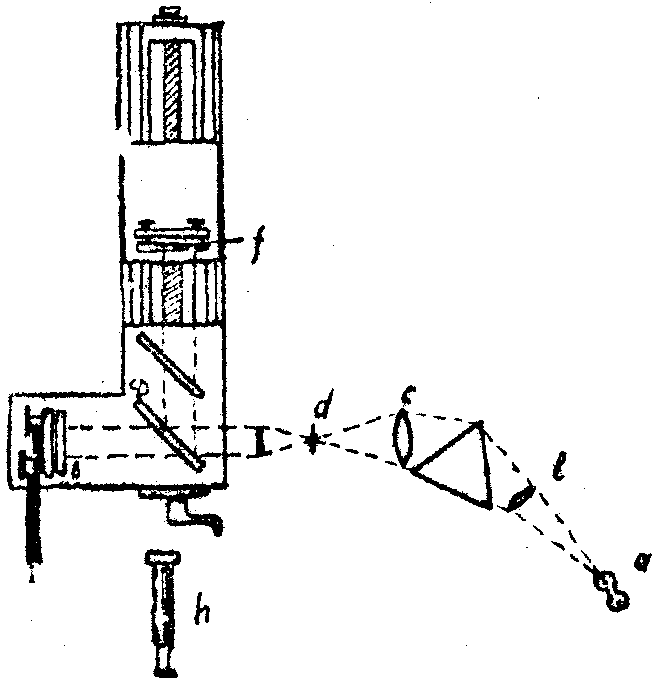
Рис.1. Схема интерферометра Майкельсона:
а - источник; Cℓ - спектроскоп.
Зеркало перемещается с помощью винта. Интерференционные полосы наблюдались через зрительную трубку h.
малоинерционных и достаточно чувствительных приёмников и автоматических средств записи. Однако во времена Майкельсона всего этого не было поэтому изменение освещённости при наблюдении через зрительную трубку он оценивал визуально.
Рассмотрим способ получения кривых видимостей. Будем считать, что отверстие в диафрагме d (рис.1) столь мало, что можно пренебречь косыми лучами в интерферометре и считать телесный угол этого отверстия W
»
0. Световой поток при фиксированной разности хода d
можно найти по формуле .
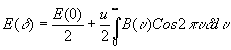 (1)
(1)
где u = W
S - геометрический фактор, S - эффективная площадь сечения пучка. Предполагая, что центр полосы спектральной кривой имеет волновое число u
0, удобно в (1) ввести в рассмотрение разность u
'=u
--u
0. Тогда эту формулу можно привести к виду
Е(d
) = P + C(d
)Cos2p
u
0d
- S(d
)Sin2p
u
0d
(2)
где
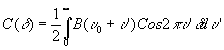 (3)
(3)
и
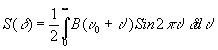 (4)
(4)
S(d
) преобразуем к виду:
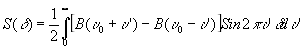 (5)
(5)
Вo всех приведённых формулах положено u=1.
а) Предположим, что B(u
) симметрична относительно u
=u
0, тогда B(u
0+u
') = В(u
0 - u
'). Следовательно, S(d
)=0 и Е(d
) приводятся к виду
Е(d
) = Р + С(d
)Соs2p
u
0d
(6)
Сравнивая (6) с (1), мы видим, что предположение о существовании точки симметрии u
=u
0 дало нам возможность выделить в интерферограмме Е(d
) быстро осциллирующую функцию Cos2p
u
0d
и её огибающую С(d
) - медленно изменяющуюся.
1) В обозначении формул будем придерживаться следующего правила: (к)- для обозначения внутри главы, (к,n) - при ссылке на n главу.
Обозначим переменную составляющую Е(d
) через
J(d
) = С(d
)Соs2p
u
0d
(7)
Майкельсон кривую видимости u
(d
) определял по формуле
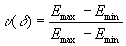 (8)
(8)
Для вычисления u
(d
) он последовательно регистрировал максимальные Еmax, и минимальные Еmin значения Е(d
) при изменении d
, начиная от d
=0 до d
=D
. Нетрудно убедиться, что Еmax и Еmin достигаются в следующих точках:
Еmax = Е(d
k) = Р + С(d
k), (d
k = l
0) (9)
и
Emin = E(d k+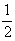 )
= P - C(d k), (d
k+
)
= P - C(d k), (d
k+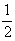 = d
k+
= d
k+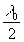 ) (10)
) (10)
В результате
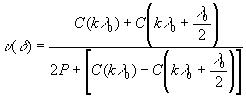 (11)
(11)
Обычно предполагается, что изменением С(d
) на промежутке [kl
0, l 0+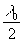 ]
можно пренебречь, и, следовательно, с достаточно хорошей степенью точности
]
можно пренебречь, и, следовательно, с достаточно хорошей степенью точности
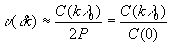 (12)
(12)
Таким образом, мы нашли, что при последовательном вычислении u
(d
) в точках d
=кl
0 можно построить график кривой видимости; при этом u
(d
) совпадает с нормированной на 1 огибающей интерферограммы J(d
). Для монохроматического источника u
(d
)=1. Если источник не является монохроматическим, то интерферограмма быстро затухает и u
(d
) также быстро спадает к нулю.
б) В общем случае, когда B(u
0+u
') ¹
B(u
0-u
') функция S(d
)¹
0 Применяя аналогичные преобразования в этом случае, найдем
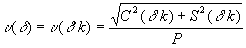 (13)
(13)
где
d 'k = d
0 +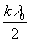
Рассмотрим способ интерпретации u
(d
).
Во всех своих работах Майкельсон при интерпретации применял метод моделей, т.е. он искусственным образом создавал кривую u
'(d
), задаваясь определённым распределением в спектре.
На основе сравнения u
'(d
) и u
(d
) он делал заключение о спектральном составе. Вначале он пользовался только средствами математики при создании u
'(d
), при этом ему удалось впервые показать, что красная линия водорода двойная и то же справедливо в отношении зелёной линии гелия. Особенно ценными были исследования красной линии кадмия, полученные при регистрации дуги электрического разряда в парах кадмия. Эта линия оказалась сингулетом, в высокой степени тонким, был найден профиль этой линии и измерена её полуширина. В дальнейшем для исследования достаточно сложных спектров им был изобретен прибор "гармонический анализатор" /10/. На этом приборе с помощью пружин он мог создавать суперпозицию колебаний с различными весами.
Укажем теперь на одно принципиальное затруднение метода Майкельсона. В общем случае B(u
) связано с С(d
) и S(d
) уравнением:
B(u ) = 8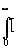 C(d
)Cos2p u 'd
+ S(d )Sin2p
u 'd ]dd
(14)
C(d
)Cos2p u 'd
+ S(d )Sin2p
u 'd ]dd
(14)
Это выражение можно преобразовать, если ввести в рассмотрение комплексное число
Z = С
+ iS = Рu
еij
, где
j =
arctg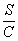
Тогда (14) приводится к виду:
B(u ) = 8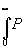 u
Cos(2p
u 'd - j
)dd (14)
u
Cos(2p
u 'd - j
)dd (14)
откуда видно, что одной кривой видимости u
(d
) может соответствовать множество спектров, отличающихся между собой разными фазовыми функциями. Релей /2/ первый обратил на это внимание и писал Майкельсону о необходимости проведения дополнительных измерений для отыскания j
. Такого рода измерения Майкельсон предполагал выполнять посредством сравнения кривых видимостей для симметричной и несимметричной полос.
Метод кривых видимостей не потерял своего значения в настоящее время, Так, Террьен /11/ в 1959 году на Теддингтонской конференции доложил об успешном применении этого метода при исследовании доплеровского расширения линий в газе. В недавней работе Хиллиарда и Шиферда /78/ с помощью видоизменённого интерферометра Майкельсона также изучалась доплеровская ширина линий.
Заканчивая обзор работ Майкельсона, хочется особо подчеркнуть, что, несмотря на значительный прогресс в технике регистрации интерферограмм и их интерпретаций, двухлучевая схема интерферометра, носящего его имя, по существу положена в основу современных Фурье-спектрометров, а оценка контрастности по формуле (8) находит широкое применение не только в оптике, но и во многих разделах науки и техники.
Следующий шаг в развитии интерференционных методов в спектроскопии связан о именами Рубенса и Вуда /13/. Они исследовали поглощение и отражение света в далекой И.К. области различными твёрдыми материалами и парами. Но для выполнения этих исследований с помощью обычных монохроматоров величина светового потока была недостаточна. Поэтому они вынуждены были обратиться к поиску более светосильных приборов. В результате они сконструировали двухлучевой интерферометр в виде двух кварцевых пластин, устанавливаемых в фокусе остаточных лучей, получаемых с помощью фокальной изоляции.
В этих опытах интерферограмма регистрировалась при изменении воздушного зазора между пластинами. Для точного определения разности хода попеременно с интерферограммой исследуемого спектра при неизменном положении пластин регистрировалась жёлтая линия натрия l
0. Максимальная разность хода в опытах не превышала 150 l
0.
Они установили, что их прибор даёт возможность использовать большую угловую апертуру и имеет меньшее светорассеяние, чем монохроматоры.
Рассмотрим, с помощью каких операций осуществлялась интерпретация интерферограмм.
Вначале рисовалась предполагаемая спектральная кривая, затем площадь под кривой разбивалась на вертикальные полоски, каждая из которых по предположению представляла значение интенсивности на соответствующей длине волны. Далее синтезировалась интерферограмма посредством суперпозиции элементарных колебаний, соответствующих полосам разбиений. Эта интерферограмма сравнивалась с опытной кривой. Если совпадение обеих кривых было удовлетворительным, то модельная кривая спектра отождествлялась со спектром источника. Сами авторы указанную методику назвали методом "проб и ошибок".
Очевидно, что между методом интерпретации кривых видимостей, разработанным Майкельсоном, и новым методом есть много общего. Прежде всего обратим внимание на то, что метод синтезирования искусственной интерферограммы можно трактовать как применение преобразования Фурье к спектральной функции. На этом основании некоторые авторы склонны видеть принципиальное отличие работы Рубенса и Вуда от метода Майкельсона и считать, что последние, по существу, реализовали метод Фурье-спектроскопии. На самом деле, как мы увидим в дальнейшем, принципиальная особенность метода Фурье-спектрометрии состоит в применении преобразования Фурье непосредственно к самой интерферограмме, в то время как у Рубенса и Вуда это преобразование используется как средство получения модельной интерферограммы. Поэтому следует считать, что их метод на самом деле принципиально не отличается от метода Майкельсона, в котором искусственная кривая видимости создавалась в общем случае на "гармоническом анализаторе" также с помощью подбора весов различных колебаний. В данном случае
мы наблюдаем различие только в средствах выполнения синтеза.
На самом деле Рубенс и Вуд, несомненно, внесли новое в развитие интерференционных методов в спектроскопии, впервые отважившись исследовать инфракрасные спектры, разработав для этого оригинальную методику измерений и аппаратуру.
Здесь мы сознательно не рассматривали вопросы, связанные с понятием когерентности света в силу того обстоятельства, что метод Фурье-спектрометрии в большинстве случаев применяют для получения относительно небольших разрешений по сравнению с собственной шириной линий, а в этом случае вполне достаточно пользоваться классическими понятиями об интерференции. Читателям, интересующимся современными представлениями о когерентности, мы рекомендуем прочесть обзор Манделя и Вульфа /14/, соответствующие главы в книге Берна и Вульфа /15/ и, наконец, обзор Стилла /40/ и книгу Строука /16/, где рассматриваются теоретические и практические аспекты интерферометрии применительно к задачам двухлучевой интерференции и голограмметрии.

