|
|
 |
 |

|
| |
Зависимость интерферограммы от угловых размеров источника
Предположим, что луч света (рис.5а) распространяется под некоторым углом i к оси интерферометра. Обозначая через d
разность хода вдоль оси, найдём, что из этого луча после светоделителя возникнут два когерентных луча, между которыми будет разность хода
d
i = d
Cosi (26)
Предположим, что i»
0, тогда
d
i »
d
(1-i2/2) (27)
Для монохроматического света световой поток на выходе интерферометра найдём по формуле (рис.5б):
E(u 1d
)du =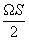 B(u
)du + B(u
)du +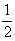 SB(u
)du SB(u
)du 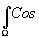 2p
u SidW 2p
u SidW
(28)
При i»
0 можно принять W
»
p
i2, отсюда из (27)
dW
= 2p
dSi/d
(29)
где d
i изменяется в пределах:
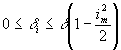 (30) (30)
Здесь im - максимальный угол наклона. В результате интегрирования (28) найдём
E(u 1d
)du =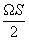 B(u
)du + B(u
)du +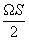 B(u
)du y (u
1d ) B(u
)du y (u
1d ) (28)
где
y (u
1d ) = 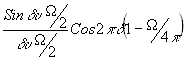 (32)
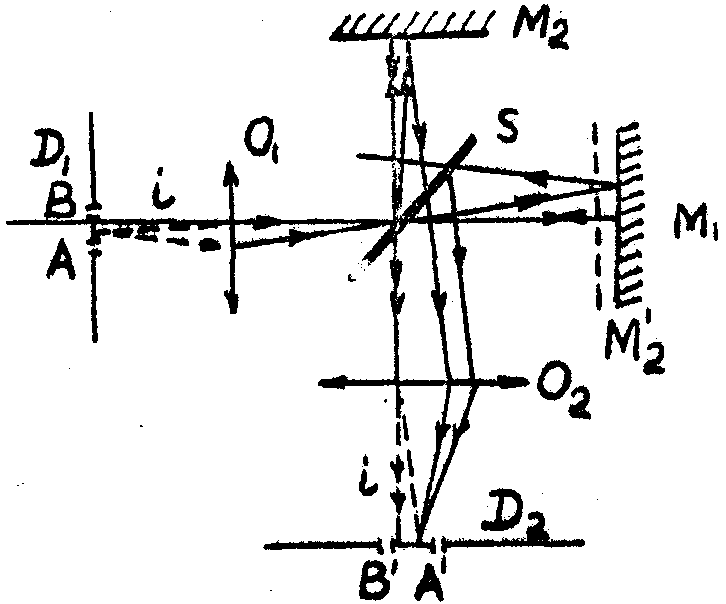
Рис.5а. Схема прохождения лучей в интерферометре Тваймана-Грина .
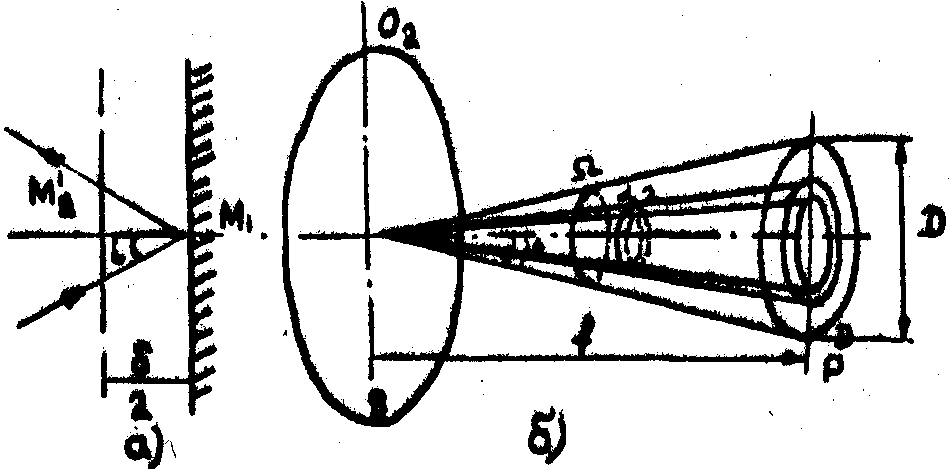
Рис.5б. К вопросу вычисления Е(u
1d
) :
а) – определение d
i; б)- интегрирование в (28) по кольцевым зонам.
Формула (31) была впервые получена Брунсом /103/ применительно к задачам метрологии, а в Фурье-спектрометрии Ж.Конн /88/.
В общем случае (сравни с (1.1)) вместо (31) имеем
E(d ) = 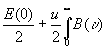 y
(u 1d )du y
(u 1d )du
(33)
Переменная часть интерферограммы вместо (25) будет равна
J(d ) = 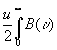 y
(u 1d )du y
(u 1d )du
(34)
Наконец, переходя к переменным w
и t найдём вместо (29)
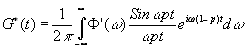 (35) (35)
где pº
W
/4p
Выражение .
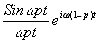
по аналогии с частотно-контрастными характеристиками оптических систем иногда называют переходной функцией интерферометра /17/
Найдём теперь связь величины светового потока E(u
,d
)du
, заключённого в телесном угле W
»
p
i2, с распределением освещённости в плоскости D2 (рис.5а). Введём в этой плоскости полярные координаты r, j
и найдём значение освещённости L (r,j
) в точке М(r,j
):
L(r,j
) = B(u
)du
Cos2p
d
iu
(rdrdj
) =
= B(u
)du
Cos2p
d
iu
(¦
2ididj
)
Откуда относительное распределение освещенности на кольце с радиусом r»
¦
i имеет простое выражение
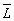
(i)
= Cos2p d
iu (36)
Подставим (27) в (36)
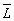
(i)
= Cos2(p u
d -u d
p i2/2) (37)
Мы видим, что при d
=0 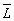 (i)=1, т.е.
имеем однородное поле освещённости при любом i.
Пусть теперь d
=кl ,
тогда (i)=1, т.е.
имеем однородное поле освещённости при любом i.
Пусть теперь d
=кl ,
тогда 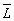 (i)=Cos2 (i)=Cos2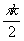 i2
и поле освещённости будет представлено системой концентрических полос равного
наклона, при этом максимумы освещённости будут иметь место при i= i2
и поле освещённости будет представлено системой концентрических полос равного
наклона, при этом максимумы освещённости будут иметь место при i=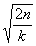 (n = 0,1,2...), в минимумы при
i=
(n = 0,1,2...), в минимумы при
i=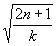 . .
Обратившись теперь к формуле (32), мы видим, что огибающая интерферограммы SinС. d
u
W
/2p
первый раз обратится в нуль при d
u
W
/2= p
. Пусть это произойдёт при d
=D
, тогда W
будет удовлетворять условию
W
R0 = 4p
(38)
С другой стороны, W будет ограничено первым
кольцом в распределении освещённости :
i=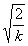
|
|
|
|
|
 |
 |
 |
 |
|
Copyright
© 1999-2004 MeDia-security,
webmaster@media-security.ru
|
|
|

